重载机械臂控制系统设计与研究*

苏 霄

(河南科技职业大学机电工程学院，河南 周口466000)

重型机械臂广泛应用于大重型物体的搬运、装配及高海拔等恶劣环境中的装配作业，提高了大负载作业效率，降低了人工成本，确保了生产的安全性[1]。国内外相关研究人员对重型机械臂进行了大量研究,结构设计方面日本日立公司设计了通用性液压控制双臂机械臂。国内在重型机械臂设计方面起步较晚，南昌新铁等公司设计了3自由度磨机衬板装配重载机械臂[2]。系统控制方面，国内外在控制算法、路径规划等方面的工业机器人理论研究较为深入。何伟、Ameri等通过人工神经网络，实现了3自由度的力/位混合控制[3-4]，控制方法控制效果较好，但主要研究对象为轻型机械臂。王从庆等基于系统动量守恒定理及拉格朗日算法，对基于平面的三连杆自由浮动刚柔耦合机械臂动力学模型进行了推导[5]。针对重型机械臂，若视作轻质长杆系统，则机械臂的高阶耦合变形项将被忽略，进而将导致机械臂弹性变形无法抑制[6]；若视作柔性系统，将产生动力学模型计算量大、维数高等问题。重型机械臂的控制方式、刚度及力学特性与以上机械臂存在较大差异，需建立专门动力学模型解决刚柔耦合抑制问题[7]。

当前重型机械臂尚存在控制构架及反馈方式优化、通讯和提升算法效率等方面问题亟需解决。未来，对于机械臂可靠性、操控性及人机交互友好性具有更高的要求，因此对重载机械臂智能化人机交互控制系统的研究具有重要意义[8]。文中基于重载机械臂工作特点，提出了基于力/视觉反馈的人机交互方式，建立了刚柔耦合动力学模型。基于人机交互的力/位反馈，提出了闭环控制算法，并在此基础上，对重载机械臂控制系统进行作业试验。

1 人机交互方式

1.1 重载机械臂结构组成

文中以7自由度重载机械臂为研究对象，其结构组成如图1所示。

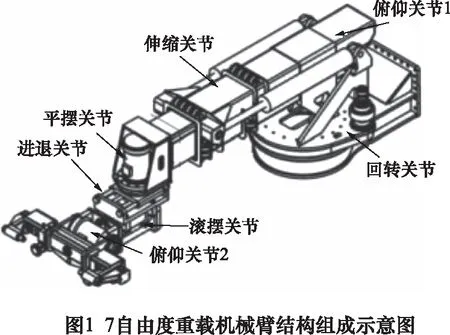
由图1可知，本文重载机械臂主要由俯仰关节、伸缩关节、进退关节、滚摆关节、平摆关节和回转关节组成，其夹持负载最大值高于2.5×103kg，有效工作半径大于2.5 m。

1.2 人机交互方式分析

文中基于力/视觉反馈的人机交互方式中力觉交换装置如图2所示。

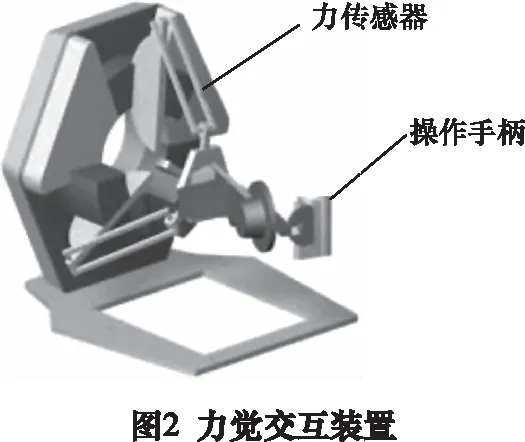
图2中，力觉交换装置控制方式为阻抗式，力传感器安装在机械臂末端抓具，通过操作手柄实时反馈6维力传感器所采集的末端作业力接触情况信息，实现6维力反馈交互。文中重载机械臂人机交互流程图如图3所示。

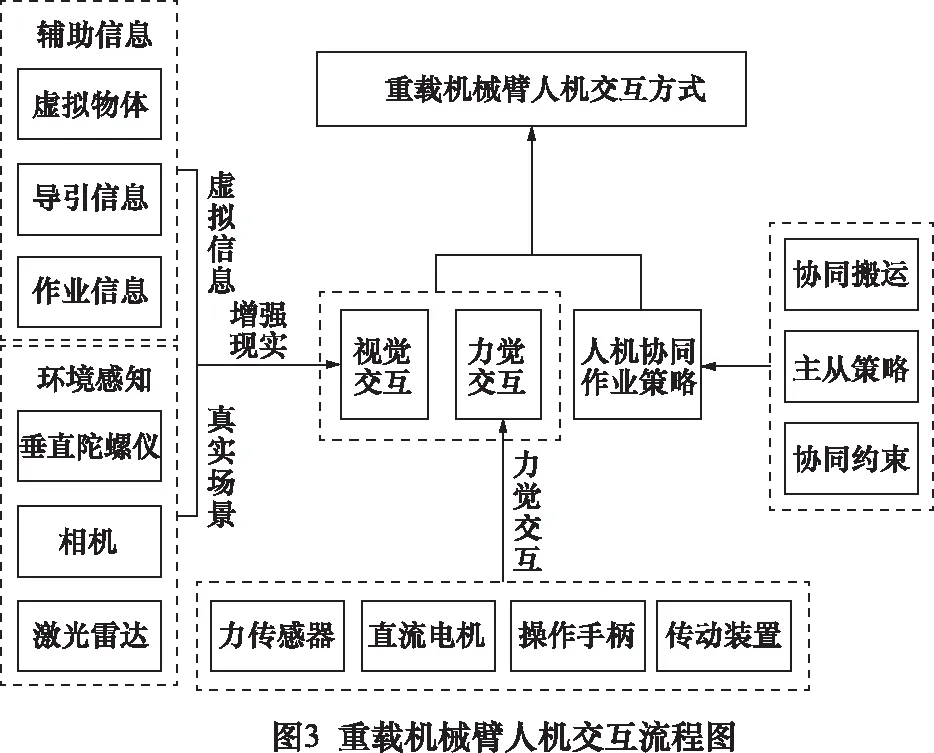
机械臂末端关节顶部安装双目相机，实时显示作业局部场景；末端关节底部安装垂直陀螺仪，对末端关节的滚转角及俯仰角进行实时测量及显示，提供准确末端关节位姿；激光雷达实时扫描、构造虚拟作业环境，提供路径规划所需信息；通过关节传感器对各关节位置进行实时测量，实现机械臂位置的实时校正。基于虚拟信息与真实环境的无缝融合及局部3维-全局视觉显示，完成机械臂增强现实视觉交互，提升交互智能型及作业过程数据的智能化显现能力。人机交互方式由力觉交互、视觉交互及人机交互策略3部分组成，实现作业人员与机械臂交互的智能化，作业的安全高效化。

2 力/位反馈控制算法

2.1 刚柔耦合特性分析

文中7自由度重载机械臂具有大负载、大重量及长臂杆的特点，在受惯性力及外力作用时，易产生弹性变形，刚柔耦合特性明显。机械臂抓具运动至作业位置时的末端关节小幅振动，对控制算法设计提出更高要求。

重载机械臂运动包括平动、转动及弹性变形3种形式，且3种形式具有高度融合性。将机械臂势能及动能进行非线性化处理，构建有效的机械臂刚柔耦合动力学模型，可实现机械臂刚柔耦合效应的抑制及提高机械臂控制的稳定性。

2.2 构建动力学模型

本文基于等效有限元法，建立重载机械臂动力学模型。等效有限元法可对目标势能及动能非线性进行精准分析。7自由度重载机械臂坐标图如图4所示。

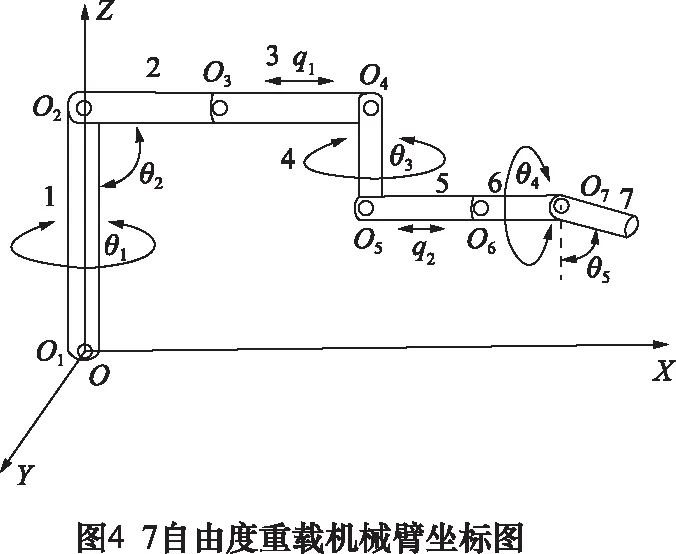
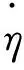
基于机械臂势能及动能的非线性，根据拉格朗日方程，将重载机械臂视为欧拉-伯努利梁，则动力学的拉格朗日表达式为:

(1)

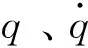
非线性化处理机械臂梁的动能，即:

(2)

式中：ρ、l为机械臂梁密度及长度；v为机械臂梁上任一点速度；M(q)为机械臂梁质量矩阵，其中:

机械臂梁振动的模态基函数为

(3)

根据刚柔耦合效应，机械臂梁势能包含弹性势能及重力势能，即:

U=UⅠ+UⅡ

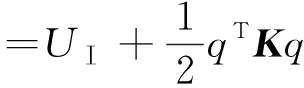
(4)

式中：UⅠ、UⅡ为机械臂梁重力势能及弹性势能，UⅠ=M(q)g；Ei为机械臂梁弹性模量；Ii为机械臂梁相对z轴转动惯量；φi为机械臂梁弹性变形；K为刚度矩阵。

将式(2)、(4)代入拉格朗日方程可得：

(5)

式中：QK为广义坐标力。

将式(5)进行整理，可得重载机械臂刚柔耦合动力学方程，即

(6)

式中：mqq、mθθ为机械臂平动部分及转动部分惯性张量；mθq为弹性形变惯性耦合；Kqq为刚度矩阵；D、v为速度一次项及二次项系数矩阵。

通过ADAMS建立重载机械臂模型[9]，如图5所示。重载机械臂动力学参数如表1所示。

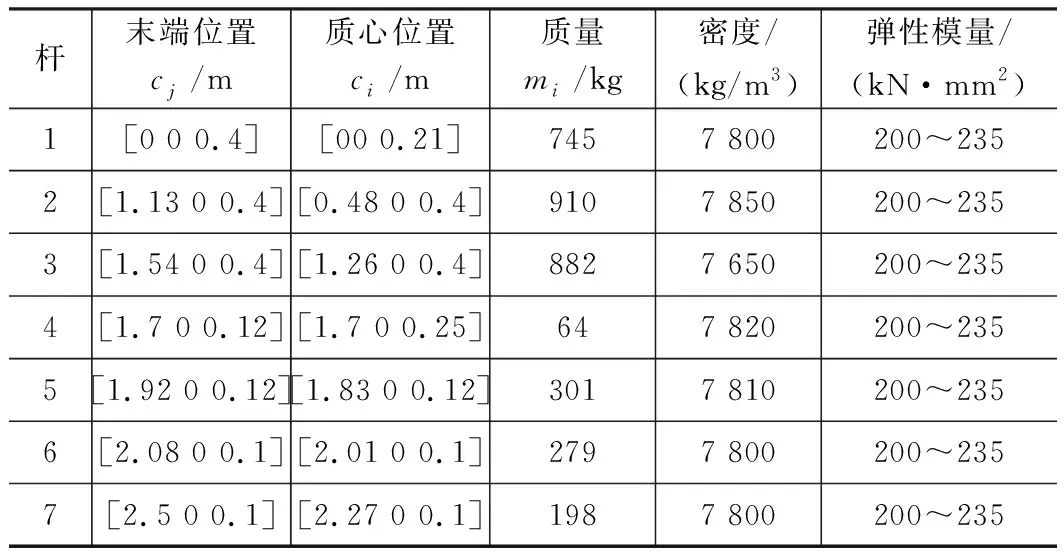
表1 重载机械臂动力学参数

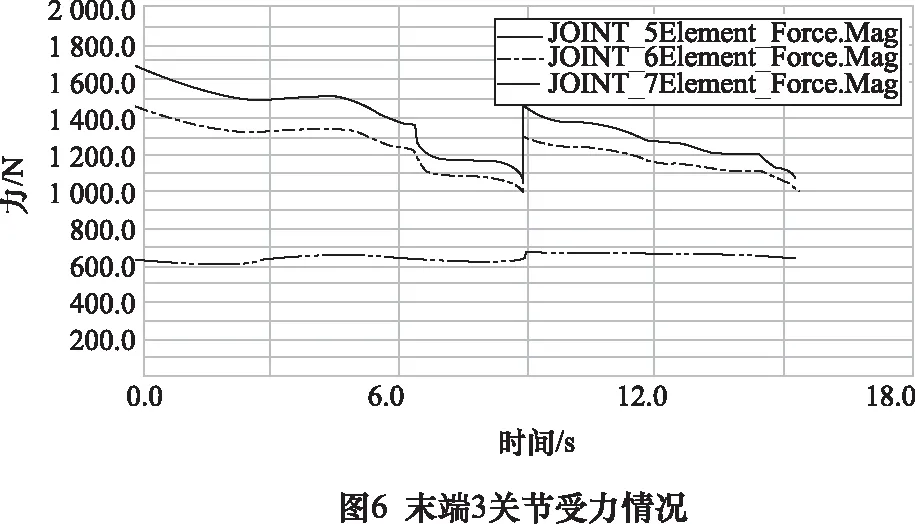
基于动力学方程及表1参数，添加ADAMS模型中各关节约束、质量及材质等。在机械臂各关节定义力矩或旋转驱动，进行动力学仿真，对机械臂动力学方程的正确性进行验证。文中选取基本式控制仿真，仿真类型为default，持续16 s。经ADAMS后处理模块，获得机械臂各关节受理情况。机械臂末端3关节受力情况如图6所示。图6中，进退关节为JOINT_5，滚摆关节为JOINT_6，俯仰关节为JOINT_7。

为了对文中方法针对刚柔耦合产生的末端振动问题的有效性进行验证，以图5中基座为轴，忽略阻尼影响，水平面上机械臂的运动为

(7)

式中：T为IF(t-NINT(t):2,2,3)；θl为起始位置与机械臂水平夹角。

采用凯恩法及有限元法分别对机械臂末端振动情况进行分析[10]，如图7所示。

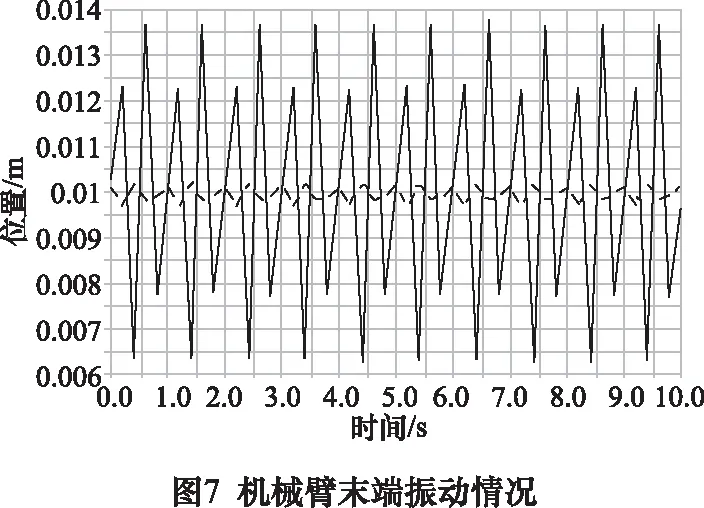
图7中，实线为采用凯恩法建立动力学模型时的末端关节振动，虚线为采用有限元法建立动力学模型时的末端关节振动。通过比较可知，刚柔耦合对机械臂末端控制具有振动影响，文中采用有限元法所建立的动力学模型可有效减小末端振动，对刚柔耦合效应抑制明显。

2.3 人机交互力/位控制算法

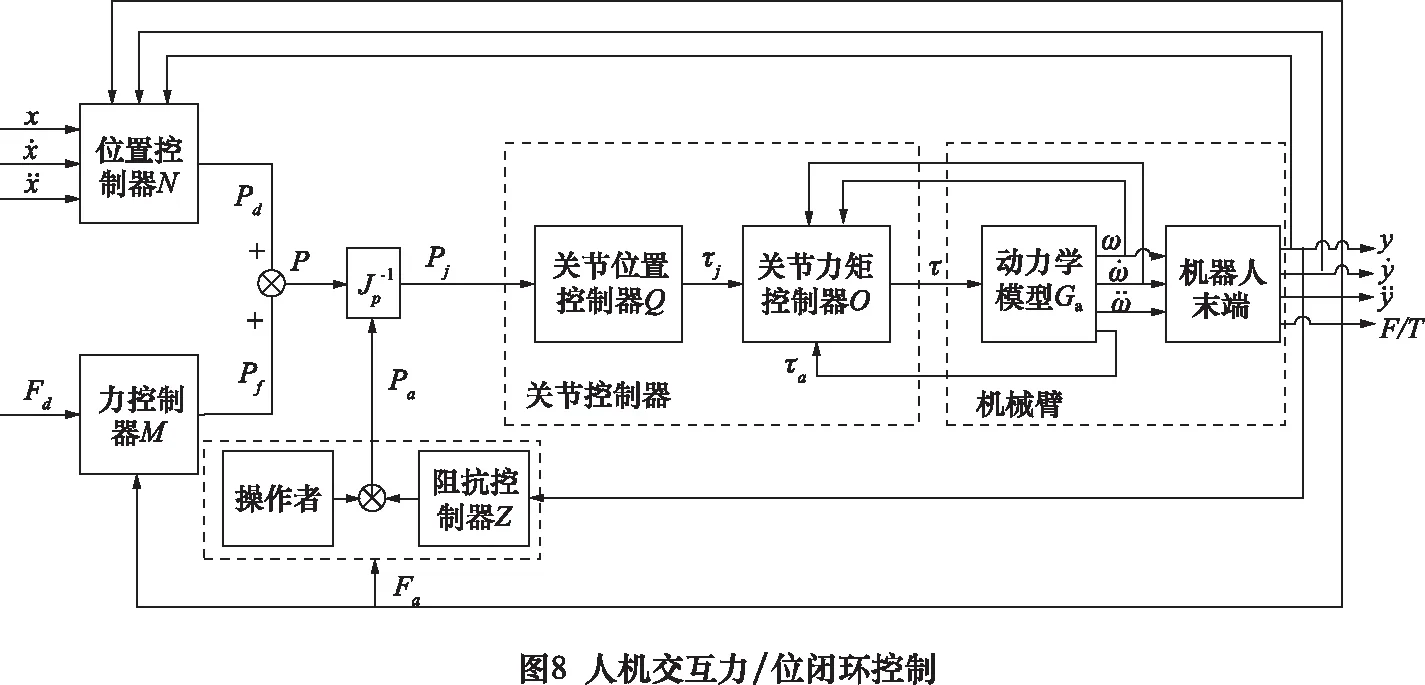
对于重载机械臂，其人机交互控制具有非线性，且尚无精准的先验公式。力/位控制为机械臂常用控制方法，文中基于刚柔耦合动力学模型，设计了人机交互力/位闭环控制算法[11]，如图8所示。

(8)

式中：Ki为可设计积分系数；Kp、Kpp为可设计比例系数。

关节力控制器及位置控制器共同构成关节控制器，其中关节位置控制器Q为比例放大器，即

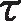
(9)

关节力矩控制器O为基于逆动力学模型的力矩计算控制器，动力学模型Ga如式(6)所示，阻抗控制实现如图9所示。

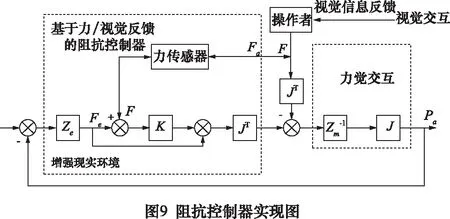
图9中，操作人员移动力觉交互装置及机械臂时，输出力为F，增强现实反馈力为Fe，设备上作用的操作人员力为Fu，J为转动惯量，Ze、Zm分别为增强现实环境及操作人员阻抗，K为力反馈增益系数。

3 设计及实验

3.1 机械臂控制系统

文中所设计重载机械臂控制系统为分层递阶体系结构，其控制系统构成如图10所示，软件系统如图11所示。

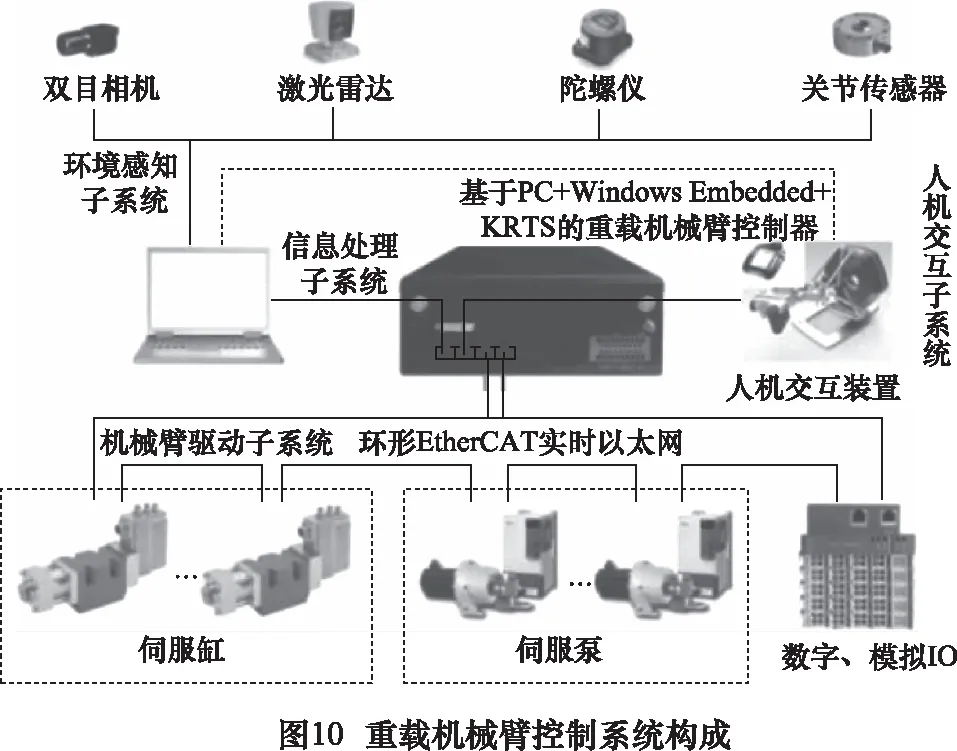
文中机械臂控制系统基于PC+Windows Embedded+KRTS运动控制器，其环境感知子系统由关节传感器、陀螺仪、激光雷达及双目相机组成，用于对障碍物及目标进行探测，搭建三维作业环境，实现为人机交互提供信息引导及路径规划等视觉交互功能。人机交互部分采用具有重力补偿功能的Delta并联机构，可提供总线、RS485、RS232等接口，实现极其灵活的精密力反馈。信息处理子系统采用配有标准网卡的多核PC，确保了控制系统硬件的高效、可靠性；操作系统采用Windows10，基于KRTS软件实现实时拓展，控制周期为500 μm，满足了运动控制实时性要求。通过EtherCAT实时总线通讯，实现机械臂信息精准、实时和高速传输。

3.2 试验测试

基于机械臂控制系统设计，搭建试验环境，如图12所示。

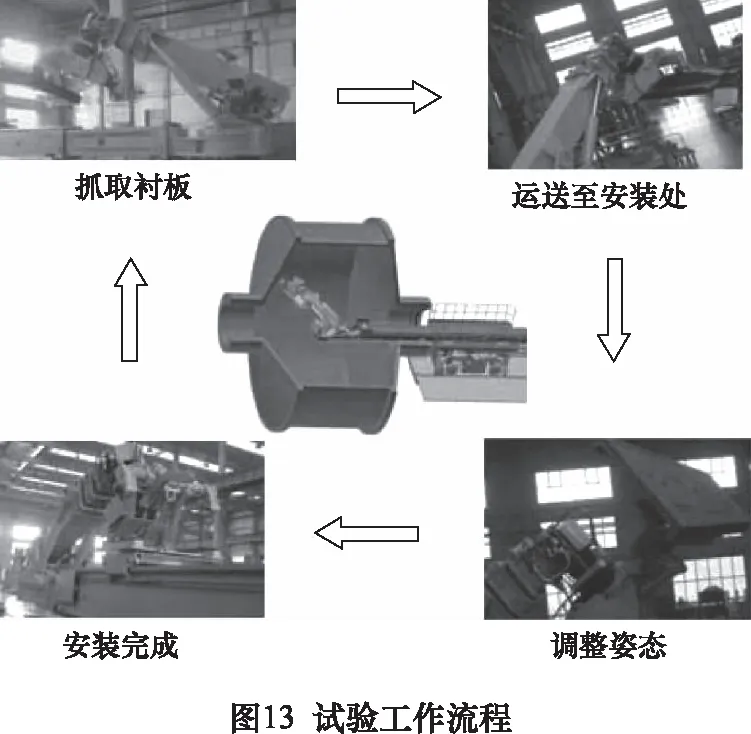
基于人机交互子系统，操作人员实时调控机械臂工作状态。作业时，机械臂由固定位置抓取衬板；通过力/视觉反馈，人机交互子系统向操作人员提供避障引导信息及路径规划；信息经处理，由驱动子系统对各关节进行驱动，将衬板吊装至磨机装配位置，并根据装配需要实时调整末端位姿；装配完成后机械臂移动至固定位置。试验工作流程如图13所示。

根据所记录试验数据，截取工作过程中某10 s试验数据，查看末端实际力及期望力、末端实际位置及期望位置，如图14、图15所示。

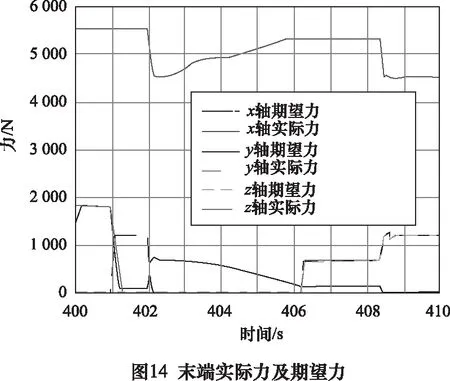
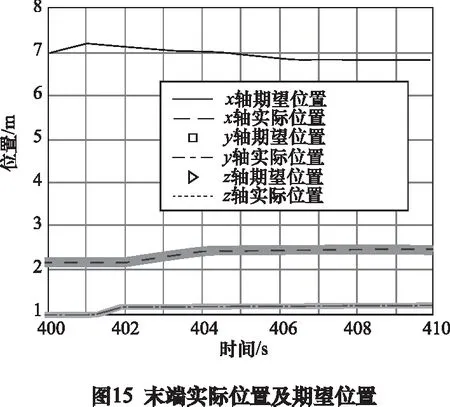
由图14、图15可知，基于文中控制系统，在3个轴向上，末端位置及末端力均可较好地跟随期望位置及期望力，刚柔耦合抑制效果较好，可达到较好效果。

按照传统方法，重载机械臂换装衬板每块需13 min左右，需10名工作人员协同合作，且由于磨机内部光线差、环境恶劣，存在较大的人身安全危险。文中基于人机交互的重载机械臂控制系统通过远端控制换装衬板，仅需3名操作人员，且每块换装仅需7 min，工作效率提高70%，且大幅度降低了工作人员的人身危害。

4 结语

文中针对当前重载机械臂控制中存在由于重载产生的刚柔耦合及人机交互性差等问题，提出了基于力/视觉反馈的人机交互控制方式。建立了7自由度重载机械臂刚柔耦合动力学模型，通过ADAMS，对动力学模型的正确性及刚柔耦合导致的末端振动抑制的有效性进行验证。基于动力学模型，提出了基于人机交互的力/位闭环控制算法，并建立了机械臂控制系统及试验环境。由试验结果可知，文中动力学模型可精准反映机械臂动态特性，人机交互性较好，作业效率大幅提高，操作人员的人身安全得到保证。