矿物浮选动力学模型及影响因素研究进展
马 强 李 育 彪 李 万 青 向 焱 李 诗 浩
(武汉理工大学资源与环境工程学院,湖北 武汉 430070)
泡沫浮选是一种以目的矿物附着于气泡为基础的物理化学分离过程[1]。由于目的组分矿物的累计回收率随浮选时间的增加而增加,本质上可将浮选过程看作一个时间-回收率过程[2-5]。浮选动力学可用来描述回收率随时间变化的过程,并通过分析矿物浮选速率的变化规律来研究各因素对浮选过程的影响。
众多学者对浮选动力学模型及其改良开展了相关研究工作,使其更加适用于浮选体系。如确定浮选动力学反应级数n;通过划分浮选组分强化动力学模型的适应性;探究引入参数对浮选速率常数k的影响规律;赋予不同k值来划分浮选组分等。以上研究推动了浮选动力学模型的快速发展,但学者们更多地研究浮选过程中各因素对浮选动力学的影响,即通过浮选动力学来量化各因素对浮选的影响,从而对现有工艺进行优化[2-8]。
为了总结浮选动力学的研究进展,本文概述了浮选动力学基本模型、发展历程及研究现状,并着重对其影响因素开展了讨论。
1 浮选动力学基本模型及发展历程
1.1 浮选动力学基本模型
浮选数学模型的构建往往决定于模型的用途,一般可分为经验模型、概率模型及动力学模型[2-3,9-10],其中,经验模型的建立对相应条件要求过于具体,一般通过尝试及错误反馈进行优化;概率模型在某些条件约束下可简化为动力学模型[3];而动力学模型主要来源于浮选动力学理论。20世纪30年代,ZUNIGA等[11]最先提出浮选动力学模型,把浮选过程近似看作一个速率过程,认为气泡与矿物颗粒的碰撞、吸附和化学反应中基本物质单元(分子、原子及离子)的作用方式一致,浮选过程中槽内目的矿物与浮选时间呈指数关系。因此,可将一级化学反应动力学模型作为浮选动力学模型。一级化学反应动力学模型为

式中:c0代表目的组分初始浓度,mg/L;c代表t时刻的目的组分浓度,mg/L;k代表反应速率常数。
进一步推导可得经典一级浮选动力学模型

式中:ε∞代表最大回收率,%;ε代表t时刻可浮矿物回收率,%;k代表浮选速率常数。
1.2 浮选动力学模型发展历程
经典一级动力学模型的建立极大地促进了浮选动力学的发展,但实际应用中,有学者把所得结果按lg(1/(1-R))-t画图,发现某些试验点明显呈非线性分布,与一级动力学模型不符[12]。于是,人们试图将一级动力学模型扩展为n级动力学模型来解释这种非线性浮选过程。1950 年,ARBITER[13]首次提出浮选速率正比于目的矿物浓度的2次方。由此,浮选动力学研究倾向于级数n的确定。后来,在二级浮选动力学模型基础上,PLAKSIN和KRASIN提出了更符合实际的n级浮选动力学模型,即

式(3)中,n为反应级数(0 在实际应用中,矿浆各组分并不是一个整体,矿浆中存在体积不均匀性。1962年,ARBITER及HARRIS[14]最先提出浮选过程中的两相模型。之后,很多研究对浮选的不均一性进行了深入研究,在两相基础上提出了三相、四相模型[12]。尽管多相浮选动力学模型对所浮矿物的不均一性进行了较好描述,但浮选回收率与时间并非线性相关,即k值不恒定。1963年,今泉常正[15]最先提出同种矿物具有不同k值分布,首次对ε-t呈非线性关系进行了解释。随后,人们的研究侧重于浮选速率常数k值的确定。1965年,WOODBURN[16]提出浮选速率常数k值服从Γ函数分布 包括均匀分布、快慢浮两点分布、多项式分布,即F(k)=a+bk+ck2+dk3均属于k值分布;后来有学者提出k值服从β函数分布 这可归类于k值随时间变化。 在此研究基础上,许多学者根据浮选流程、矿石性质推导出了不同的浮选动力学模型,包括经典一级动力学[11]、一级矩形分布[17]、二级动力学[13]、二级矩形分布[18]、陈子鸣[19]、刘逸超[20]、许长连[21]、哥利科夫[19]及吴亦瑞三重逼近[22]等模型。 浮选动力学模型中,以经典一级动力学模型n应用最为广泛。为使其更加适用于实际浮选,众多学者开展了k值分布密度函数、k值的组成及变化规律等方面的研究工作,进一步提高了拟合精度。如于洋等[23]对黑钨矿、白钨矿及萤石的浮选分离过程进行了浮选动力学研究,发现浮选速率常数k值持续变化,柠檬酸为抑制剂能显著扩大三者的浮选速率差异,在经典一级动力学模型基础上得到优化后的分速模型 式中,f和s分别代表快浮和慢浮;ε∞代表最高回收率,%;ε代表累计回收率,%。修正后的模型精度得到了显著提高。AI等[24]为了研究细粒黑钨矿的浮选特性及其浮选动力学,在经典一级模型基础上提出了新模型,即 式中:ε1∞及k1分别为易浮黑钨矿的最大回收率及浮选速率常数,ε2∞和k2分别为难浮黑钨矿的最大回收率及浮选速率常数。通过与经典一级模型、修正一级模型、矩形分布一级模型及二级模型对比,可知新模型对细粒黑钨矿具有最好的拟合效果。 在实际矿物浮选过程中,一方面可通过浮选动力学模型从微观层面阐述目的矿物浮选特性,另一方面又可以根据浮选动力学结果评价浮选药剂作用效果。金会心等[25]在研究富稀土磷矿的浮选动力学变化规律时引入了时间滞后因子θ,对经典一级动力学模型进行修正,从而推导出富稀土磷矿反浮选动力学速率模型,即 对该模型结果进行方差分析,可知捕收剂WF-01用量对修正速率常数kmod影响最大,抑制剂H3PO4用量对选择性指数SI影响最大。 为了更直观对比并优化不同模型,CHEN等[26]对长焰煤气泡浮选与油泡浮选动力学进行了研究,并对6种动力学模型同时进行了优化。结果表明:采用油泡浮选相较气泡浮选更容易在前中期提高精煤产率,相比于其他模型,经典一级动力学模型能较好地描述气泡浮选,但6种模型对油泡浮选结果拟合偏差都较大。为了更好地描述油泡浮选,在浮选动力学模型中减去时间常数t,即可平衡油气泡浮选延迟,提升了拟合精度。6种改进的模型中,经典一级模型最适合描述油泡浮选过程。 为了扩展经典一级动力学模型的通用性及可行性,使之能在广泛条件下描述浮选过程,KLIM⁃PELR[17]提出了一级矩形分布浮选动力学模型。BAYAT等[27]在研究粒度分布对土耳其闪锌矿浮选行为的影响时,发现d80=0.125 mm进料粒度下的浮选行为与一级矩形分布模型相吻合,适应性最好。 目前,一级浮选动力学模型的研究主要集中在提高模型的适用性及拟合精度,通过划分不同浮选组分、引入不同参数等手段不断对模型进行优化,使其更符合实际浮选规律,扩大模型适应面。尽管针对一级动力学模型的优化已经开展了不少研究工作,但模型所适应的矿石类别仍具有一定局限性,相关系统性研究工作还有待加强。 当浮选动力学模型中的级数n取2或3时,可分别得到二、三级浮选动力学模型。相较于一级浮选动力学模型,多级浮选动力学模型考虑到矿物类型、矿浆密度、矿浆pH、药剂添加量及充气量等的影响,能够更好地描述浮选过程。LIAO等[28]以低阶煤为目的矿物,采用气泡浮选和油泡浮选对其浮选特性及浮选动力学进行了研究,拟合结果表明低阶煤在2种浮选法中均可用二级浮选动力学模型描述。为了更广泛地表示浮选速率常数k的分布,KLIMPEL[18]提出了二级矩形分布浮选动力学模型,SALEHA[29]的研究结果表明二级矩形分布浮选动力学模型能较好地描述铁矿石浮选结果。 为使所得浮选数据按lg(1/(1-R))-t作图呈线性分布,VOLKOYAZ[30]提出了三级浮选动力学模型。在实际应用中,针对矿物颗粒被捕获时上升速度不同,采用三级浮选动力学模型可对慢浮矿物浮选特性进行描述。罗成等[31]以窄粒级煤泥为浮选对象,进行了反应级数n的研究。结果表明:浮选初期,当n分别取1、2、3时,浮选动力学模型均与实际浮选数据吻合。浮选后期,只有一级动力学模型与实际吻合,二、三级浮选动力学模型拟合值均偏小。这归因于一级浮选动力学收敛速度更快,随着反应级数n取值增大,模型收敛速度越慢,而煤泥上浮速度较快,使二、三级浮选动力学不能很好描述煤泥浮选过程。因此,二、三级浮选动力学模型更适用于慢浮矿物。 为增强浮选动力学模型对实际浮选过程的适应性,BROZEK[32]提出了非整数级浮选动力学模型,即 BU等[33]对某煤泥特定粒级(-188µm和-100µm)进行了拟合,发现非整数级浮选动力学模型能更好地描述浮选过程。 针对浮选动力学模型的研究表明,现阶段浮选动力学模型的发展建立在经典一级浮选动力学模型基础上,大致分为两个方向:①针对实际矿石性质引入不同参数,或对浮选组分进行细分,得到不同组分的浮选速率常数;②通过试验验证以确定模型反应级数n,得到与之对应的最佳取值,提高模型拟合精度。 浮选动力学模型在经典一级动力学模型的基础上得到了较大发展,增强了浮选动力学模型对复杂矿物的适应性。但是浮选过程复杂,包括矿粒和气泡的相互接触、疏水矿粒在气泡上粘附形成矿化气泡、矿化气泡进入泡沫层及精矿泡沫层的排出[34]。在这些浮选过程中,矿物颗粒自身性质(如矿物晶体结构、颗粒大小及形状)、浮选工艺参数(如浮选药剂种类及用量)及浮选机结构参数等均可对其产生影响[2,4,6,9,35-36],总结各个因素对浮选动力学模型的影响对优化模型的适应性具有重要意义。 矿物晶体结构对浮选特性有很大影响,如晶胞原子缺失、晶型转变及晶格膨胀均会影响矿物的晶体结构,从而导致晶胞周期性势场、电子分布以及能带结构的改变[37],并最终影响矿物浮游性能[38-39]。SALMANI等[40]研究了晶体溶解对浮选动力学的影响,结果表明,溶解会导致脉石矿物表面晶格定位离子减少,伴生脉石矿物浮选速率常数显著减小。 同样,矿物粒度对浮选动力学各参数影响显著,ABKHOSHK[41]在间歇浮选槽中运用非线性方程对浮选速率常数与煤粒度的关系进行了量化,方差分析结果表明,相比最大理论回收率,粒度对浮选速率常数影响更大;模糊模型计算结果显示,粒度大小、浮选时间及累计回收率的3D模型可对不同粒度煤的累计回收率进行预测。ZHANG等[2]研究了粒度对褐煤反浮选动力学的影响,运用1stOpt软件对试验结果进行6种模型拟合并预测浮选速率常数、最大灰分回收率与粒度的关系。结果表明:除经典一级动力学模型外,其他模型均能很好地拟合不同粒级的试验数据。当粒级为150~250µm时浮选速度常数最大,这可能是由于浮选中碰撞、附着及分离等关键步骤决定,由于颗粒较高的脱附率,在此过程中细粒级矿物与气泡碰撞概率较低、粗粒级矿物浮选速率低。通过反浮选效率指数对褐煤的反浮选效果与粒度的关系作了进一步评价,发现在给定时间内,与所研究的窄粒级组分相比,褐煤粒级为-425µm时反浮选动力学参数最佳。YALCIN等[42]对黄铁矿型金矿浮选动力学进行了研究,结果表明:金对应浮选速率常数与粒度呈负相关;相比一级模型,采用二级模型时,浮选速率常数对磨矿粒度有着更高的依赖性,相关系数均大于0.998。 矿物颗粒延伸率、圆度及形状特征影响其与气泡的相互作用,进而影响矿物浮选分离效率[43-44]。DEHGHANIF等[45]研究了颗粒形状对磁铁矿单矿物浮选动力学的影响,发现具有较高延伸率和较低圆度的颗粒具有较大的浮选动力学常数。此外,有石英颗粒存在时,磁铁矿颗粒形状对浮选影响更大,浮选动力学常数也比单独浮选磁铁矿时高。MA等[46]采用6种浮选动力学模型研究了焦煤颗粒形状对浮选动力学的影响,结果同样表明:由于颗粒与气泡之间的作用面积增大,颗粒延伸率与可浮性呈正相关,且焦煤浮选符合一级矩形分布浮选动力学模型。RAHIMI等[47]研究了不同研磨方法对石英颗粒形状及浮选的影响,结果表明:石英颗粒形状显著影响浮选速率常数,较高延伸率及低圆度颗粒具有较高可浮性。 浮选过程中除了矿物本身性质的影响,浮选药剂也起极其重要的影响[48]。NATARAJAN等[49]研究了N-芳香异羟肟酸不同取代基对加拿大某镍矿浮选动力学的影响。结果表明,相比黄药,N-苯基-N-(2,6二甲基苯基)羟胺浮选镍黄铁矿时具有更好选择性及较高的一级浮选动力学速率常数。KLIMPEL[50]研究了烃链长度对各种硫烃捕收剂性能的影响。结果表明:与传统水溶性捕收剂相比,硫烃捕收剂可降低药剂成本,增大浮选速率常数,提高对硫化铁的选择性。ZHU等[5]通过咪唑离子液体(1-烷基-3-甲基咪唑氯化物)配制微乳液浮选煤泥,所得煤泥的可燃体回收率及净灰分含量与正十二烷浮选效果类似,不但节省捕收剂约43%,且无需起泡剂,是煤泥浮选的高效捕收剂,浮选过程符合一级矩阵分布模型。张晋霞等[51]对石英、蓝晶石和黑云母在pH=6.5时的浮选动力学进行了研究。结果表明,抑制剂淀粉可扩大3种矿物浮选速率差异,模型拟合发现经典一级动力学模型与实际数据相吻合。 常用的浮选机有机械式浮选机、浮选柱及反应器、分离器式浮选机[52-53],其类别、叶轮倾角及转速、充气量等都会影响气泡与矿粒的相互作用,进而影响浮选动力学。 GAO等[54]研究了操作参数对BF-40浮选机浮选动力学的影响,对比分析3种不同叶轮转速和浸入深度,发现主轴转速为151 r/min、叶轮浸入深度1 195 mm时,BF-40型机械搅拌浮选机能获得最佳浮选动力学参数。 KOH等[55]通过CFD方法研究了Denver自充气式浮选机叶轮转速对气流的影响,并进行了浮选动力学模拟。研究发现:空气通过叶轮的旋转作用进入矿浆,空气流速由叶轮产生的吸入压力及进气阀到叶轮输送轴上的摩擦损失共同决定。浮选动力学模拟表明:重力作用对颗粒附着影响显著,可通过控制叶轮转速调节气泡上升速度达到提高浮选速率的目的。KOH等[56]进一步通过CFD计算模型模拟自充气式浮选机槽内多尺寸气泡与颗粒的附着速率。结果表明:气泡分布对颗粒浮选速率影响显著,全尺寸气泡分布的浮选速率高于单尺寸气泡的浮选速率,更有利于优化浮选槽设计,提升浮选槽工作效率。韩伟[57]针对JFC-150型浮选机内流特性,研究了浮选机充气量、矿浆含气量及气泡矿化概率等对浮选动力学参数的影响。结果表明:较高的叶轮转速和较大的充气压力会增强分离区及输运区的湍流强度,从而增大颗粒悬浮能力及脱附作用力,最佳叶轮转速为110~130 r/min、充气压力为50~60 kPa。 LI等[58]研究了充气式旋流浮选柱充气量对不同粒径组分浮选特性的影响,并在此基础上提出了一种新的浮选动力学模型。结果表明:充气量的增加能显著提高粗、细煤泥浮选回收率,特别是粗煤泥的分选。对于0.25~0.50 mm的粗粒级,新模型中煤泥R2值(相关系数)接近1,SSE(误差平方和)接近0,表明该粒级浮选与新模型吻合。 张晓燕[59]采用类似于浮选柱的自制搅拌式浮选槽研究了叶轮转速对煤泥浮选动力学的影响。结果表明:提高叶轮转速可提高精煤产率及可燃体回收率。由模型拟合可知煤泥浮选符合一级动力学模型,过高转速会降低k值。因此,叶轮转速不宜过高。叶轮低转速时,不同密度细煤泥对应的k值差异较大,对于高、低密度级煤泥,叶轮转速分别为600 r/min、800 r/min时可获得最佳浮选动力学常数。 FILIPPOV等[60]对在反应器、分离器中黄铜矿、石英混合矿浮选动力学进行了研究。结果表明:采用反应器、分离器有助于黄铜粗精矿浮选回收率的提高,增大其浮选速率,这是因为反应器/分离器存在不同的区域,可将气流分散到气泡中,增强气泡与颗粒的附着。 除了上述浮选设备外,有学者研究了新型振荡网格浮选槽(OGC)对浮选动力学的影响。CHANGUNDA等[61]以甲基化石英为研究对象,对OGC能量输入引起浮选动力学的变化进行了研究。结果表明,浮选速率常数随功率强度的增加呈近似线性关系,可能是由于输入的能量在湍流环境中较好地促进颗粒-气泡接触。田全志等[62]以低阶煤为研究对象,对能量输入引起的可浮性进行了研究。结果表明:低能量输入不利于增加气泡与矿粒的碰撞吸附概率,高能量输入易夹带高灰细泥。因此,输入中等能量能够促进低阶煤浮选,符合一级矩阵模型,而高能量输入时则符合经典一级模型。 除了矿物粒径和形状、药剂、浮选设备等参数影响浮选动力学外,矿浆浓度、泡沫滞留时间、超声波处理及研磨介质种类等都可对矿物浮选动力学产生影响。 缪亚兵等[63]研究了萤石矿浆质量浓度对浮选动力学的影响。结果表明:增大萤石矿浆浓度能够增大浮选速率常数。郑雪华[64]研究了浮选过程中泡沫滞留时间对浮选速率常数k值的影响。结果表明:浮选速率常数k随泡沫滞留时间呈指数式减小。 MAO等[65]研究了高灰分褐煤浮选特性,包括超声矿浆层、泡沫层对褐煤浮选动力学的影响。结果表明:常规浮选及超声矿浆层、泡沫层浮选对应浮选动力学速率常数k分别为2.313 3、0.837 3和4.211 4,且泡沫层超声处理时可浮性差的褐煤浮选符合二级矩形分布模型。因此,在泡沫层超声能够显著增大浮选速率常数k,为褐煤超声浮选提供指导依据。 为了解释磨矿介质种类对矿物浮选动力学的影响,ZHANG等[66]研究了不同磨矿介质对黄铁矿浮选动力学的影响。结果表明:陶瓷球研磨黄铁矿时,分散在黄铁矿表面的铁氧络合物较少,可明显增加黄铁矿浮选累计回收率。模型拟合结果表明:以陶瓷球为研磨介质时,浮选过程符合一级动力学,而以铸铁球为研磨介质时,一级、二级动力学模型均与结果相吻合。由此可知,不同磨矿介质造成铁氧络合物含量差异,影响黄铁矿浮选动力学,其中采用陶瓷球作为研磨介质能较好地提高黄铁矿浮选效率。 总结可知,不同因素往往可通过3个方面影响矿物浮选动力学:①改变矿物晶体结构;②影响矿物颗粒与气泡间的粘附概率;③改变矿物表面亲、疏水性。 矿物浮选动力学的影响因素涉及矿物晶体结构、形状和表观形貌、药剂种类、浮选设备及实验过程中各种参数的变化。为了优化浮选工艺流程、改造工艺设备并提升浮选过程中智能化控制,研究工作者开展了大量的科学研究。当前浮选动力学主要从模型参数的引入或浮选组分的划分、n值的确定两大方向发展。但是,浮选动力学模型发展存在两方面的不足,其一为现阶段浮选动力学模型更适用于一元矿物的浮选过程,对多元矿物分选难以很好地进行描述;其二,在实际浮选中,影响矿物浮选动力学模型的因素不是单独存在,而现阶段浮选动力学模型的建立与优化并不能统筹以上各因素。 鉴于此,为了不断优化浮选动力学模型来更好地描述浮选过程,通过计算机强大的分析处理能力,运用理论计算对影响浮选动力学的各因素进行评估,并结合工艺矿物学、浮选机内矿浆的流体运动规律来加强浮选动力学模型对不同矿物、不同因素下浮选过程的适应性,是未来需要重点关注的研究方向。此外,基于浮选动力学分析对浮选设备进行优化,有利于提高矿物浮选分离效率,具有重要现实及科学意义。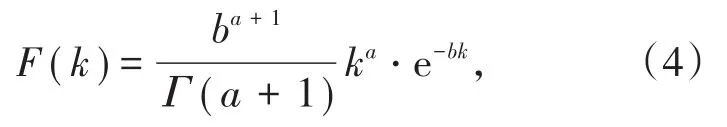
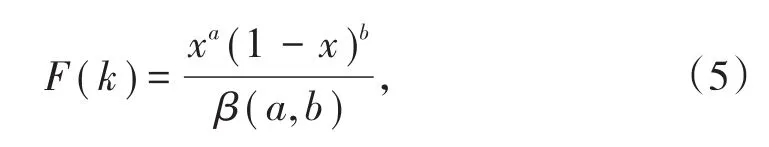
2 浮选动力学模型研究现状
2.1 n=1的浮选动力学模型

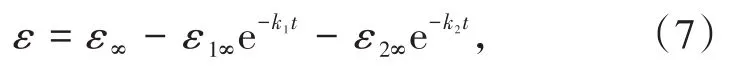

2.2 n>1的浮选动力学模型
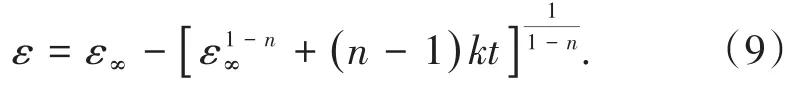
3 浮选动力学模型的影响因素
3.1 矿物颗粒自身性质的影响
3.2 浮选工艺参数的影响
3.3 浮选设备的影响
3.4 其他因素的影响
4 结论与展望

