海洋黏土超固结性和结构性对沉垫基础离底吸附力的影响

龙 月，张 琪，叶冠林

(1. 上海交通大学 海洋工程国家重点实验室，上海 200240; 2. 上海交通大学 土木工程系，上海 200240)

我国近海区域海床表面广泛存在一层深厚软黏土，具有一定的超固结性与结构性。如图1所示，自升式海洋平台沉垫基础利用大底面坐稳，对海床承载力要求低，避免了传统桩靴式基础插入深度深、拔桩时间长、安装效率低等问题，十分适用于我国的黏土海床条件。沉垫基础作业过程一般包括航行—坐底—在位—离底，其在离底上拔时会产生负孔压[1]，进而受到底质对其吸附力的作用，因此沉垫基础离底需要提供大于其水下自重的上拔力，是影响基础离底阶段安全的重要因素。

图1 桩靴基础与沉垫基础对比Fig. 1 Comparison between spudcan and mat foundation

Ninomiya等[2-4]采用室内试验的方法对吸附力问题做了大量研究，认为吸附力由黏滞力(viscous force)、底部黏附力(bottom adhesion)和侧摩阻力(side friction)构成。Vesic[5]通过对圆形平板锚吸附力的研究阐述了吸附力的产生机理，认为吸附力产生的原因是平板锚上下表面的孔隙水压差。Sawicki等[6]假定海床为多孔可变形饱和土体，通过理论分析和数值模拟分析了结构物从海床中拔出的过程，结果表明上拔是轴向卸载过程，底部孔压由正变负，因此产生吸附力。Chen等[7]通过离心机试验研究了上拔速率、上拔偏心和踢脚长度对防沉板离底吸附力的影响，试验结果表明减小上拔速率以及偏心上拔能够减小吸附力。Zhou等[8]采用有限元方法研究了黏土中桩靴上拔的吸附力问题，并分析了土体性质和固结时间对吸附力的影响。国内金广泉等[9]通过试验研究了结构体接触介质、结构体入陷深度以及结构体底面形状对吸附力的影响，认为吸附力为结构物下底质结构破坏产生。韩丽华等[10]通过室内模型试验研究了结构物底面积和底面铺设砂垫层等对吸附力的影响，结果表明单位面积吸附力不受尺寸效应影响。刘润等[11]对具有不同开孔形式的防沉板进行上拔试验，揭示了上拔阻力的构成和发展规律，阐明了开孔率和有效宽度对上拔阻力和接触面间吸附力的影响规律。丁红岩等[12]对桩靴上拔进行数值模拟，提出其上拔阻力由桩靴上部阻力和底部吸力组成，且分析了平台工作荷载、上拔速度和贯入深度的影响规律。Zhou等[13]将结构物上拔分为3个阶段，包括无间隔阶段、过渡阶段和有间隔阶段，但是很少有数值模型能够模拟结构物上拔的完整过程。

可以看到，针对结构物所受吸附力，国内外学者采用室内试验和数值模拟的方法做出大量研究，但是较少涉及黏土海床超固结性和结构性对离底吸附力的影响。因此文中建立了模型模拟沉垫基础上拔的完整过程，并通过现场试验来验证该模型的合理性，分析了沉垫基础作业全过程海床土体的孔压发展规律，探讨了土体的超固结性、结构性对土体孔压和位移的影响。

1 数值模型理论基础

1.1 黏土弹塑性本构模型

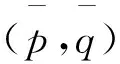
(1)

(2)

式中:R*和R分别为正常屈服面与上负荷面以及下负荷面与上负荷面的相似比。

图2 p-q平面中的下负荷面，正常屈服面和上负荷面关系图[14]Fig. 2 Subloading, normal and superloading yield surfaces in p-q plane[14]

对重塑土的正常固结应力状态(p*,q*)，屈服面方程为：

(3)

由当前应力状态(p,q)来表达，即：

(4)

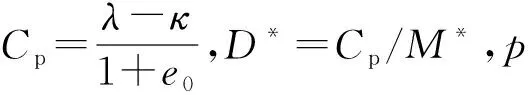
协调方程为：

(5)

模型中采用相关联流动法则，即：

(6)

对于R和R*的发展式，有：

(7)

(8)

式中：m和a为材料参数，分别控制了状态变量R和R*的变化速率。因此可得：

(9)

(10)

(11)

有关系：

(12)

式中：σij为应力张量。

由式(12)可以求得：

(13)

将式(9)、(10)、(11)、(13)代入协调方程式(5)，则有：

(14)

将应变张量增量分解为弹性和塑性部分，相应的弹性部分由Hooke定理确定：

(15)

将式(12)代入式(15)，则可得到：

(16)

其中，正变量Λ的表达式为：

(17)

式中：

(18)

将式(13)代入式(18)可得：

(19)

式中：

(20)

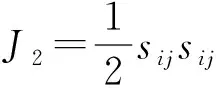
加载准则为：

(21)

1.2 黏结接触模型

沉垫基础作业过程中，沉淀基础与土体接触面上发生压缩以及张开，为模拟上拔的整个过程，采用可以模拟黏结材料强度破坏和刚度衰减的黏结接触模型。该模型常用于模拟近似无厚度的黏结单元，其假设接触面应力与相对位移在达到黏结强度之前是线弹性的[15]，即存在有：

(22)

式中：σ为应力，δ为相对位移，K代表黏结材料的刚度系数，下标n表示法向，s和t为两个切向方向。一般来说土体—结构相互作用时常忽略其耦合参数[16]，而上拔时，沉垫基础主要受法向作用，切线方向相对位移很小可忽略不计，在此仅考虑Knn的取值[17]。

(23)

图3 线性损伤演变规律曲线Fig. 3 Linear damage evolution curve

损伤演变准则，即损伤本构模型，用以描述刚度衰减的全过程。Guilio[19]针对黏结模型分析解耦问题中接触面损伤本构呈双线性、线性—抛物线、指数、梯形进行比较计算，认为双线性模型在计算精度和效率上最能满足要求，因此模型中采用双线性损伤演变，即在刚度衰减过程中力与位移呈线性变化，如图3所示。损伤系数D可以表示为：

(24)

图4 单元试验模型示意Fig. 4 Element test model diagram

2 UMAT子程序验证

ABAQUS/Standard支持用户子程序，采用Fortran语言编写的UMAT即用户自定义材料属性接口，可根据主程序传入的应变增量，更新应力增量及相关状态变量，再传入主程序中求解平衡方程。因此可将上述黏土弹塑性本构通过UMAT子程序嵌入ABAQUS/Standard进行计算。

表1 UMAT检验模型土体参数表[20-21]Tab. 1 Soil parameter of UMAT test model[20-21]

图5 UMAT子程序与MCC本构三轴排水试验结果对比Fig. 5 Comparison of UMAT subroutine and MCC constitutive triaxial test results

由图5中可以看出，不考虑超固结性和结构性时，UMAT子程序与ABAQUS自带的修正剑桥模型结果基本一致。此外，考虑土体超固结性时，土体发生了应变软化现象，且有剪胀的趋势；考虑结构性时，土体硬化程度和土体剪缩程度小于正常固结土。因此该UMAT子程序计算结果合理，且可以反映土体超固结性和结构性的影响，可采用该子程序开展进一步的研究工作。

3 数值模型验证

3.1 现场模型试验原理与过程

为了验证数值模型计算沉垫基础离底吸附力的合理性和准确性，在东海长兴岛进行了现场模型试验。试验所在地为软黏土海床，水深5 m左右。沉垫模型为中空构造，为2 m×2 m×1 m六面体，自重10 t左右。在沉垫基础模型上安装了7个孔压计，其中6个孔压计位于模型底部，1个位于模型顶部，如图6所示。同时，起吊装置与沉垫基础用拉力计和位移计连接，通过拉力计读数来判断坐底是否稳定以及上拔是否完成。

图6 沉垫模型示意Fig. 6 Diagram of the test mat model

试验中将模型箱缓慢吊起，将其缓慢放入海水中，当拉力计读数接近0时，模型箱与海床接触。模型坐底2.5 d后上拔，上拔时间为4 min，整个过程记录孔压计和土压力计读数，采集频率为25 s一次。

以往研究表明，负孔压形成的吸力占模型所受吸附力的大部分，因此采用底面超孔压形成的吸力最大值作为试验中模型受到的吸附力[22-23]。底面超孔压为底面平均孔压减去静水压力，在试验中可通过底面平均孔压减去顶面孔压和由于模型高度形成的水压差10 kPa之和得到，即：

UW=Ubottom-Utop-10

(25)

式中：UW为底面超孔压；Ubottom为沉垫基础底面孔压计读数平均值；Utop为沉垫基础顶面孔压计读数，表征静水压力。

3.2 数值模型建立

根据现场试验建立相同沉垫尺寸的数值模型(2 m×2 m×1 m)，为忽略边界效应的影响，海床土体为边长20 m的正六面体。数值模型边界条件为：海床底部约束x、y、z三个方向的位移，侧面约束法向位移，土体表面除基础底部外为排水边界，其余边界均为面均不排水边界[24]。分析步设置包括：1) 地应力平衡；2) 基础坐底阶段，考虑沉垫基础自重；3) 土体固结阶段，固结时间为2.5 d；4) 基础上拔阶段，采用位移控制。参考以往对于上海软土的研究[21,25]，土体材料如表2所示，沉垫基础设置为弹性模量非常大的线弹性模型，弹性模量为1012kPa，泊松比为0.3。数值模型在沉垫基础附近进行了网格加密处理，经过网格独立性验证后确定模型网格划分如图7所示。

表2 计算模型土体参数Tab. 2 Soil parameters of calculation model

图7 数值模型网格划分Fig. 7 Mesh of the numerical model

3.3 数值模拟和现场数据的对比

从黏结接触模型可知接触面刚度系数K值表征应力与位移之间的关系，在此采用试验中沉垫基础上拔负孔压增长阶段的底部孔压—位移关系曲线的斜率来表示该值，可得黏结接触模型中K值取9 700 kPa/m-1。

在数值模拟中以沉垫基础底部土体的平均负超孔压表征离底吸附力，以沉垫基础上表面平均竖向应力σ33减去其自重表征上拔力。图8(a)为数值模拟和试验值离底孔压随上拔时间发展规律，两者较为一致，其最大负孔压均为-17 kPa左右。图8(b)为模拟离底吸附力和实测吸附力的对比，图中实测离底吸附力为试验过程中所测最大吸附力值，上拔过程中模拟吸附力和上拔力都随时间逐渐增大，但后者增长速率较快，在25 s时上拔力等于吸附力，可认为该时刻模型开始离底，此时的吸附力即为模型上拔离底需要克服的离底吸附力，从图中可以看出模拟离底吸附力与试验离底吸附力基本一致。

图8 模拟值与试验值对比Fig. 8 Comparison between test model and numerical model

4 数值结果与分析

4.1 土体负孔压与竖向位移

选取沉垫基础底部正下方土体P1、距中心位置1/8B(B为基础宽度)处土体P2、距中心位置1/4B处土体P3，基础边缘处土体P4，土体位置如图9所示。上述P1，P2，P3位置处土体上拔阶段孔压随时间的变化曲线如图10(a)。由图10(a)可以看出，在上拔之初土体孔压不为0，这是因为固结阶段孔压消散不完全，进而导致P4处土体负孔压最大，而P2处土体的负孔压最小。上拔初期孔压出现小幅度的上升，上拔期间，沉垫底部各位置土体孔压发展趋势类似，超孔压由正孔压逐渐转变为负孔压，负孔压达到最大值后又逐渐降低，逐渐发展成正孔压，与其他室内试验结果一致[26]。对P1，P3，P4位置处土体的竖向位移如图10(b)所示，由图可知，沉垫基础边缘位置处土体位移小于中心位置处，则可知沉垫基础边缘处土体接触面首先发生刚度衰减，即边缘率先发生离底，这与文献[26]规律一致。上拔初期土体随沉垫基础上拔有些微上移，但始终处于压缩状态，此后在重力作用下土体逐渐回落。

4.2 黏土超固结性影响分析

由于我国近海黏土海床常具有一定的弱超固结性，因此首先分析黏土超固结性对沉垫基础的影响。图11为沉垫基础底部中心点位置作业全周期的孔压发展规律。可以看出，不同超固结性土体的各个阶段孔压发展趋势类似。OCR值越大，坐底和固结阶段超孔压越小，负孔压最大值越大。由前文数值结果和以往研究可知，沉垫基础所受负孔压基本可以表征其所受吸附力，考虑到沉垫基础完全离底后其下部土体的负孔压值不表征吸附力，因此可得图12。由图12可知随着OCR的增大，沉垫基础底部所受吸附力越大，且OCR值越大，该影响越显著。沉垫基础上拔完成后，土体顶部的超孔压值也随着OCR的增大而增大，这是因为OCR增大，土体孔隙变小，则土体固结速率变慢。

图9 土体位置示意Fig. 9 Schematic diagram of the location of soil

图10 沉垫基础下方不同位置处土体孔压和竖向位移变化曲线Fig. 10 Pore pressure and vertical displacement curve of different locations under mat foundation

图11 土体超固结性超孔压影响关系曲线Fig. 11 Influence of over-consolidation on excess pore pressure

图12 土体超固结性吸附力影响关系曲线Fig. 12 Influence of over-consolidation on suction force

4.3 黏土结构性影响分析

图13 土体结构性超孔压影响关系曲线Fig. 13 Influence of structural property on excess pore pressure

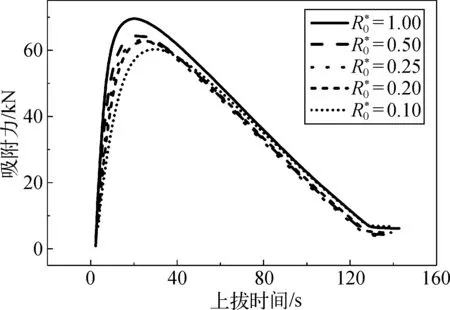
图14 土体结构性吸附力影响关系曲线Fig. 14 Influence of structural property on suction force

5 结 语

通过对自升式海洋平台沉垫基础在超固结性和结构性黏土海床上作业工况的数值模拟和现场试验，主要得到以下结论：

1) 黏结接触模型可以精确地模拟出整个上拔过程中沉垫与土体的相互作用问题。将UMAT子程序和MCC模型进行三轴排水试验对比计算，验证了UMAT子程序的正确性及超固结性、结构性的模拟情况；

2) 沉垫基础上拔过程中数值与现场试验结果吻合较好，最大负孔压均为-17 kPa左右；上拔25 s时数值上拔力和离底吸附力相交且基本与试验测得的离底吸附力相等；

3) 沉垫基础上拔过程中，基础下方土体孔压在小幅上升后迅速达到最大负孔压，然后负孔压逐渐消散。土体固结时间为2.5 d情况下，基础边缘处的离底吸附力最大，且基础边缘处首先发生刚度衰减；

4) 海洋黏土的超固结性与结构性对沉垫基础离底吸附力影响显著。土体超固结性越强，沉垫基础离底负孔压越大，离底吸附力越大，且随着超固结性的增强影响效果越显著；通过分析土体结构性对沉垫基础的影响，土体结构性越强，沉垫基础离底负孔压越小，离底吸附力也越小，到达最大吸附力所需的时间越长，上拔结束时吸附力十分接近。