通信接收机的任意采样率转换方法

熊韬

（广州海格通信集团股份有限公司，广东广州，510663）

0 引言

在通信接收机产品设计中，AD采样器件与信号处理器（如FPGA、DSP）的采样时钟常常不一致，为保证对AD器件所得的接收采样信号后续进行有效处理，需对AD采样信号进行采样率转换至信号处理器的采样时钟。

按照数字信号处理的相关内容可以知道，接收机采样率转换分为整数倍采样率抽取和非整倍抽取，整数倍抽取技术十分成熟，通过多级CIC滤波器和半带滤波进行抽取可完成，而传统的非整数倍抽取首先需要将非整数倍数转化成分子、分母都可能十分大的分数，然后进行分子倍插值以及分母倍抽取。这种方法尽管在理论上可行并取得良好的效果，但在实际中受限于运算量非常大的制约，对器件要求苛刻，无法在工程上得到普遍运用。FARROW[1-5]结构滤波器为解决上述问题能在计算复杂度做了极大优化，但是该方法只在部分小数倍（如0.1倍，0.9倍）区间抽取展现较好效果，而在0.5倍抽取附近抽取时效果欠佳，信号的畸变较大。本文在利用矩阵理论中的LU分解的基础上，利用数值分析中的三次样条插值方法，提出了一种计算量较小的任意采样率转换方法，该方法对于处理时延要求不高的中、低速吞吐量的波形的接收信号的速率转换具有非常好的效果。

1 采样率转换原理

所谓采样率转换是指由于实际工程中接收机AD采样器件的采样率fAD与信号处理器件FPGA（或DSP等其他信号处理器件）的采样时钟fFPGA经常不一致，为保证数据能按照FPGA的采样时钟进行处理需要将AD采样后的数据的采样率转换成FPGA所需的采样率。

假设接收机AD采样后的离散信号序列为y1(k)，该序列对应期望的采样率fAD，接收机采样速率的转换可以通过如图1所示信号重构后的重采样模型来描述：

图1 信号重构后的重采样原理

图1的基本原理是将离散点x(k)曲线拟合成xa(t)，然后再对连续曲线按照采样频率fFPGA对连续信号xa(t)进行重新采样，采样后的序列即为y(m)。对曲线拟合的方法很多，最简单的是线性插值和抛物线插值，但从保证曲线完整性的角度来看，三次样条插值的拟合方法效果最好，该方法可通过矩阵理论的特殊处理使得系数求解的过程运算复杂度较低。

2 三次样条插值理论

在工程实践中，工程师经常会用到插值来拟合曲线。最简单的插值方法便是在相邻的两个样本点之间进行线性插值，但是这种拟合的光滑性太差，导致这种插值方法尽管简单但是拟合误差较大。通常为了提高拟合曲线的精度，一般都会用三次样条曲线插值，下面给出简单的三次样条插值的叙述。

3 任意采样率转换方法

4 仿真分析

对上述方法进行了数值仿真，仿真中发送的信号为载波频率为 ±3MHz、±1.5MHz、±0.75MHz和 ±0.375MHz的正弦波信号叠加后的信号，接收信号AD器件的采样率设置为fAD= 4 0MHz，信号处理器FPGA所需的采样时钟设置为fFPGA= 3 4MHz。经过本文所提的采样率转换方法前后的信号频谱以及时序图如图2、图3。

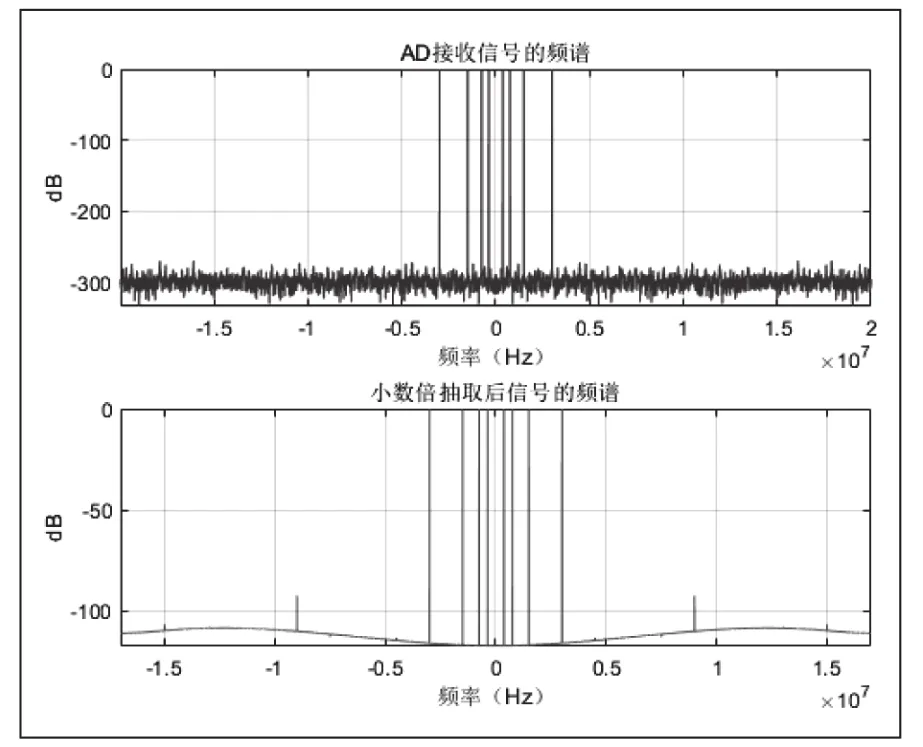
图2 AD采样信号在小数倍抽取前后频谱仿真效果

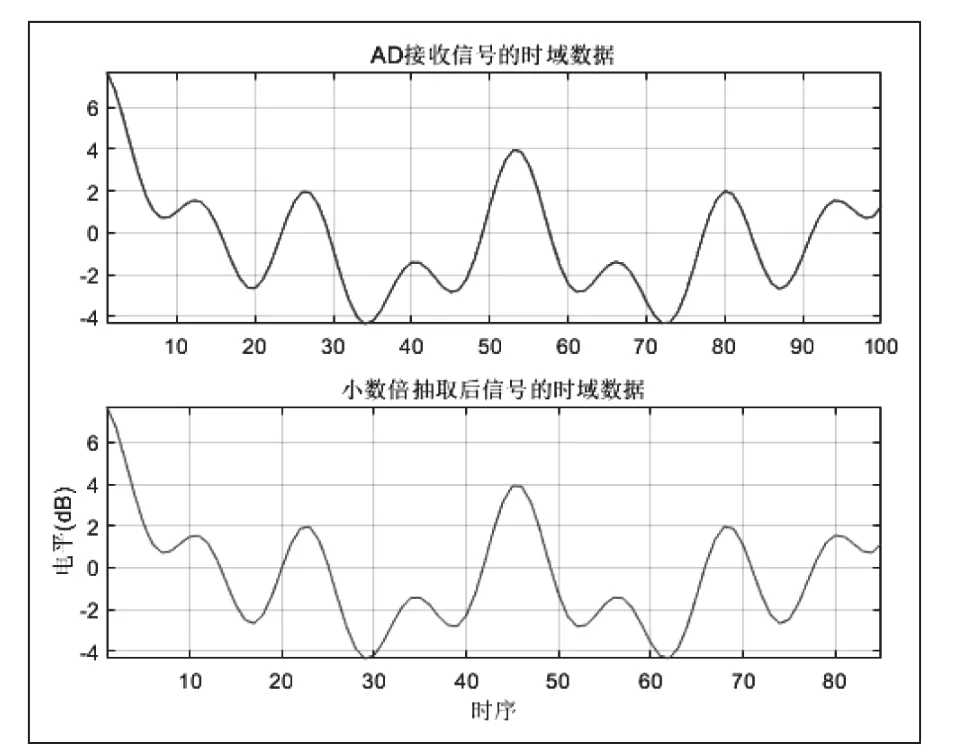
图3 AD采样信号在小数倍抽取前后时序仿真效果

从仿真效果可以看到，上一节所提方法得到的抽取信号的时序及频谱形状保持接收信号的特性，说明了该方法具备良好可行性。

5 结束语

本文所提方法在数值分析中的三次样条理论基础上利用Toeplitz矩阵理论进行优化得到计算量小的采样率转换方法，该方法能很好保持接收信号的时域及频域特性，仿真结果表明转换性能良好。需要说明的是该方法在对速率要求不高的中、低速接收信号能起到很好速率转换的效果，但是对于高速接收信号而言使用该方法还是会造成一定的处理时延，这将是后续研究的重点。