基于分数阶PIλ控制的VIENNA整流器的研究

刘丹玉

(黑龙江科技大学电气与控制工程学院，黑龙江哈尔滨，150022)

0 引言

VIENNA整流器作为电动汽车充电桩技术的前级PFC能实现提高功率因数并且控制输出电压稳定的目的。对于VIENNA整流器来说，通常采用电流和电压的双闭环控制。文献[1]电压外环采用PI控制，电流内环采用功率滑模控制，其对功率直接控制取得了较好的效果，但其算法存在共振进而造成延时。文献[2]提出的单周期控制方法取得了较好的效果，但其控制方式依赖模拟电路实现，不便于数字化设计。文献[3]电流环使用滞环控制，其具有鲁棒性好、动态响应快等优点，但存在开关频率变动、各相电流之间互相影响的缺陷。

传统PI控制有动态特性差、参数整定繁琐等缺点，故本文将分数阶PI控制[4]应用到VIENNA整流器中，建立了VIENNA整流器的数学模型，利用PSO算法整定参数。最后，通过仿真验证了分数阶PI控制的可行性。

1 VIENNA整流器的数学模型

VIENNA拓扑结构如图1所示。

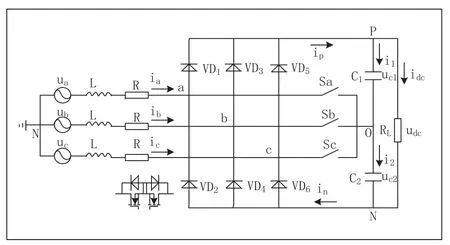
图1 VIENNA拓扑结构

建立VIENNA整流器在d-q坐标系下的数学模型如下：

其中ud、uq是网侧电压在d-q轴的分量；id、iq是网侧电流在d-q轴的分量；vd、vq是d-q轴的开关状态函数。

2 FPID控制器

FPID记为PIλD，比传统PID增加了两个自由度λ、μ，故控制阶次的范围大大提高，也提高了系统控制精度和灵活性，其结构图如下：

其传递函数为：

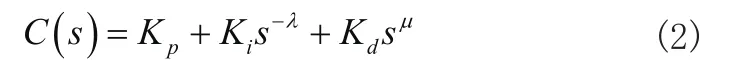
当λ＞0，μ=0时，C(s)=Kp+Ki s-λ，此时为分数阶PI控制器。电流内环采用FOPI控制进行前馈解耦实现独立控制，所得控制方程如下：

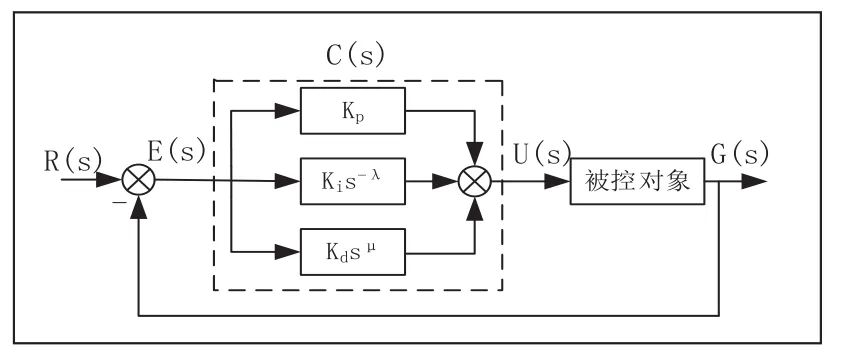
图2 FPID系统结构图

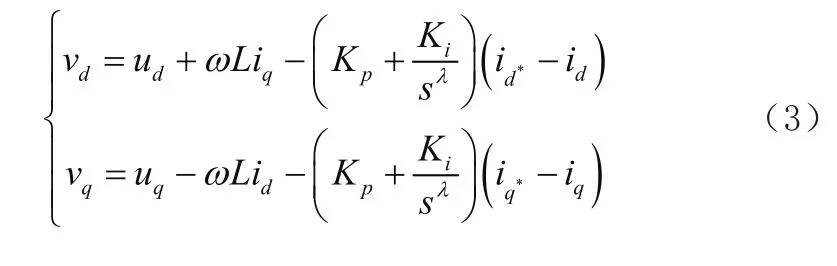
2.1 sγ的拟合和离散化

分数阶微积分算子sγ在Bode图中其幅频特性是一条斜率为20γdB/dec的斜线，相频特性为平行于X轴的直线。而要寻找一个幅相特性相同的整数阶函数是不可能的，故通常在一定频率范围(ωb,ωh)找出具有近似特性的高阶函数来代替分数阶函数。本文采用Oustaloup进行近似化处理。例如对s0.2在（0.01，1000）范围内近似处理，如图3所示，可以看出s0.2的幅频特性曲线的斜率大致为4dB/dec，相频特性曲线大致为18°的直线，与其理论的幅相特性几乎一致，说明Oustaloup近似法可行。

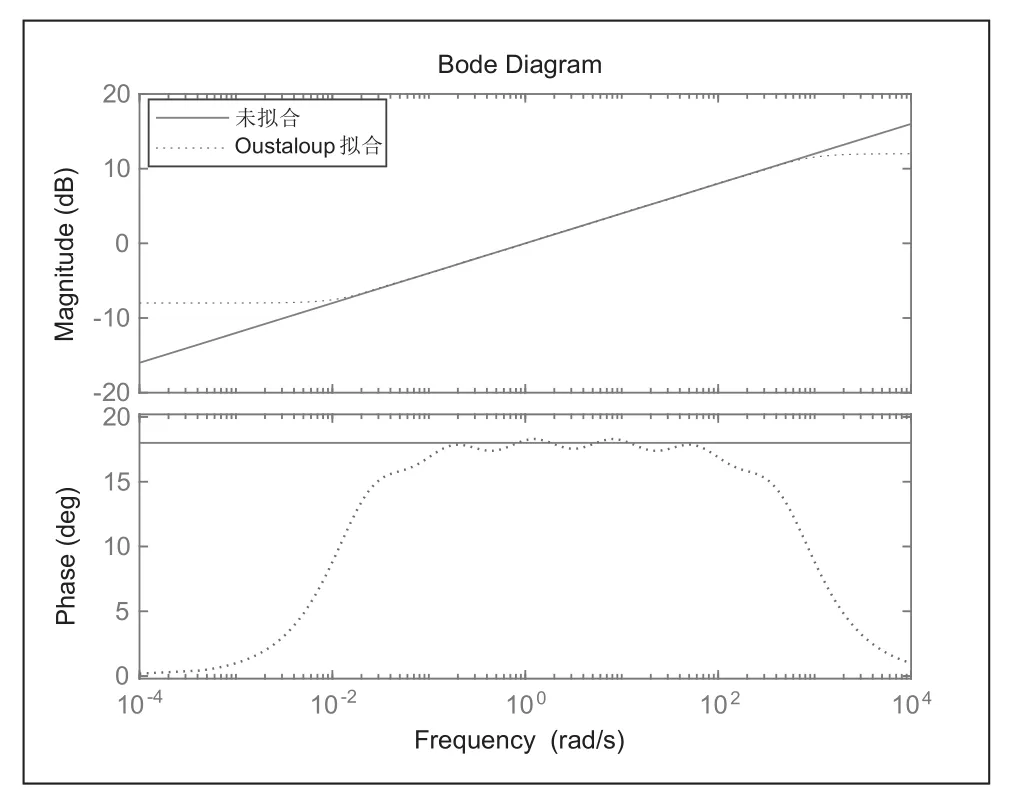
图3 Oustaloup近似拟合后的Bode图

因近似后是高阶系统，故用z变换理论将上述高阶系统离散化进而用数字实现。

3 基于ITAE指标的粒子群算法整定参数

PSO算法中粒子的速度和位置更新公式如下：

ω是惯性因子，C1、C2是加速度常数，r1、r2是区间[0,1]上的随机数，Pid是某个粒子的最优解，Pgd是粒子群的最优解。

ITAE准则的表达式为

基于ITAE指标的PSO算法整定参数过程如图4。

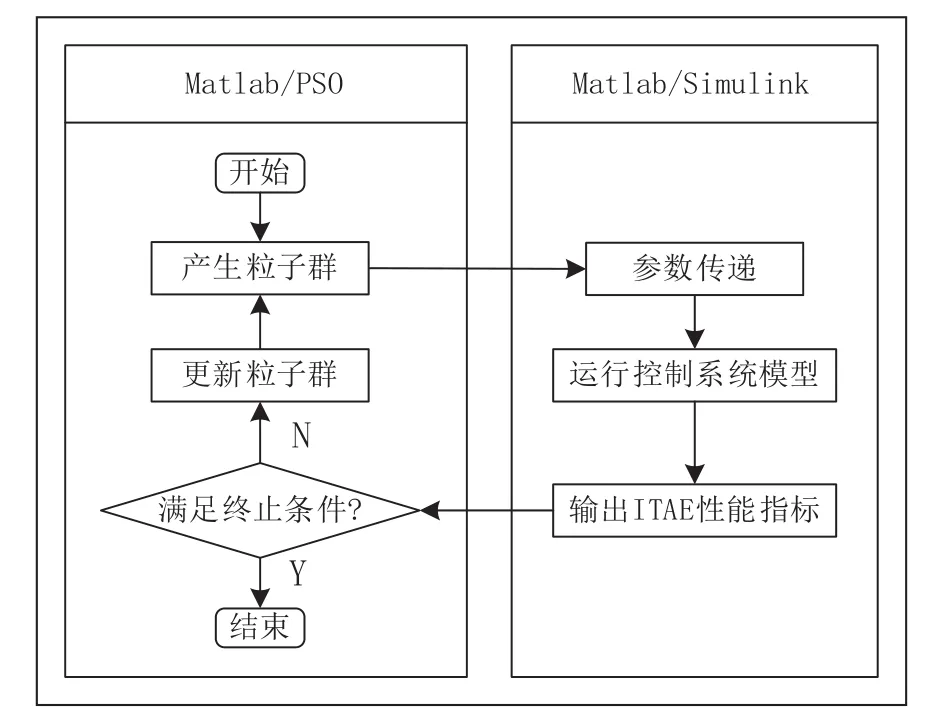
图4 PSO算法参数整定过程

4 仿真验证

在Simulink中搭建如图5所示的模型，其调制策略采用SVPWM[5]，其参数三相交流电压有效值为220V，直流侧给定电压值700V，额定频率50Hz，开关频率10kHz，电阻负载50Ω，滤波电感5mH，直流侧电容3.5mF。

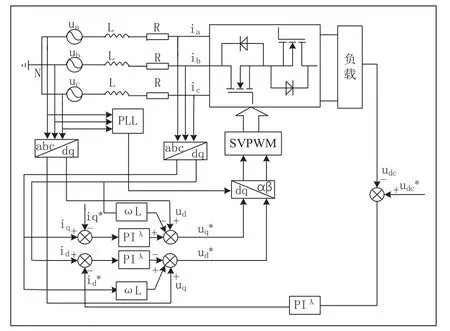
图5 VIENNA整流器控制框图

基于PSO算法整定电流环FOPI参数时，将两个误差信号取绝对值后相加形成一个ITAE指标。运行后得电流环控制器如式

由图6知，采用FOPI控制的电压与电流相位几乎一致，功率因数接近1。由图7知，电流THD含量减小为1.82%。由图8知，在系统受到扰动后，FOPI控制的鲁棒性明显更好。

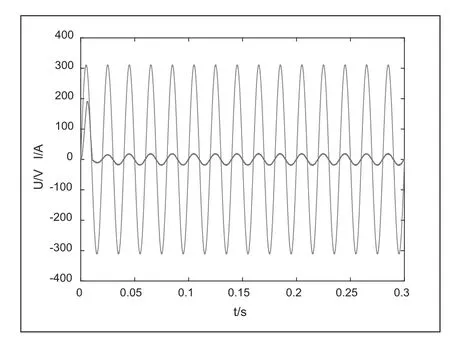
图6 相电压和相电流

图7 FOPI控制下电流THD

图8 加入扰动后输出电压对比

5 结论

电流电压环都采用FOPI控制，并在Matlab中进行验证。结果显示：电流内环的FOPI前馈解耦控制能够实现解耦减小误差，使交流侧电流很好地跟踪电压，功率因数接近1，降低了电流谐波含量；电压外环的FOPI控制使直流输出的电压更加稳定，较IOPI控制有更好的鲁棒性。