基于遗传算法的轴流风机后导叶匹配性优化*

凌杰达 王 军 丁炎炎 肖千豪 王 华

（1.华中科技大学能源与动力工程学院；2.广东肇庆德通有限公司）

0 引言

轴流风机后导叶在回收叶轮出口动能中起到重要作用。但在设计阶段对后导叶的重视程度远不及叶轮，设计出的后导叶因与转子不匹配，致使风机性能下滑。因此对后导叶进行匹配转子的优化设计具有重要意义。

不少研究人员使用各种优化技术对叶轮叶片进行改型优化，Lotfi 等人[1]针对二维透平叶栅的升阻比或损失系数，直接使用单目标遗传算法优化叶型。黄友根等人[2]和Kim 等人[3]均使用多目标遗传算法结合近似模型对轴流风机的叶片叶型进行优化，取得一定成果。Seo 等人[4]通过修改积叠线的方法改变叶片弯掠角，并使用响应面法（RSM）得到一低速轴流风机效率最优对应的叶片弯掠角，实现风机的优化。然而目前轴流风机后导叶匹配性优化的研究还不够全面，孟丽[5]通过单独变化后导叶的叶片数、叶间距离、叶型和安装角，一定程度提升了风机性能。肖云峰[6]利用DOE 方法优化的动调风机后导叶叶型，减小了动叶出口二次流损失。Lee[7]则在选定翼型的情况下调整后导叶积叠线，运用最速下降法和共轭梯度法寻找到一个最优弯掠叶型。但上述工作存在设计变量单一，或未考虑设计参数间的交互影响与参数空间连续性等不足。

本文以一款工业用R+S单级轴流风机为原型，基于EBF 神经网络模型和多岛遗传算法对其后导叶结构进行优化设计，获得的全局最优解提高了风机最大流量工况下的性能参数。最后对优化结果与后导叶内部流场做一定分析。

1 风机CFD数值模拟

1.1 风机模型

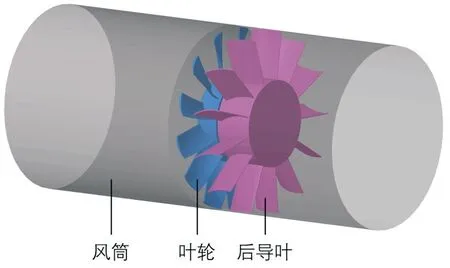
图1 风机模型示意图Fig.1 Model of fan

研究对象为工业用R+S 单级轴流风机，如图1 所示。叶轮主要尺寸参数为：外径D2=900mm，叶片数Z=12，叶顶间隙δr=4.5mm；后导叶顶部与机壳贴合无间隙，因此后导叶外径DR=909mm，叶片数为17。叶轮和后导叶轮毂比均为0.48。叶轮前后有内径为909mm的风筒与风机机壳相连，后导叶轮毂内安置电机。一般情况下，电机对风机内部气流影响较小。

1.2 数值方法

为获得更加准确的预测结果，对整机进行全流道三维数值模拟。叶轮和后导叶网格使用结构化网格以提升网格质量，风机进口与出口段均延长2 倍叶轮外径。经过网格无关性验证，确定叶轮与导叶部分网格数约为4.5×106，总网格数约为5.5×106。为了减小网格对不同方案的计算结果的影响，在后文建立神经网络模型样本时，前后延长段网格不变，叶轮及导叶区域的网格划分参数设置相同。叶轮与导叶网格如图2 所示。

图2 叶轮及导叶网格划分Fig.2 Meshing of impeller and guide vane

使用ANSYS FLUENT 软件进行定常数值计算，采用Realizable κ-ε湍流模型、标准壁面函数和SIMPLE算法进行计算，介质为不可压缩空气。叶轮区域转速设置为1 450r/min。边界条件为速度进口，压力出口，残差设置为1×10-5。

1.3 后导叶参数化

在后导叶叶片数、叶片厚度等其他参数不变的情况下，考虑叶片自身形状（翼型弦长b、翼型弯曲角θ）与位置（叶片安装角βb、轴向间隙δa）对风机性能的影响。

为便于生产制造，后导叶采用单圆弧翼型，且沿翼展无扭转。通过翼型弦长b和翼型弯曲角θ两个设计参数，即可完全控制翼型几何形状。如图3 所示，沿半径方向同时收放点P1，P2可使翼型弯曲角固定而弦长改变（如翼型A至B）；仅竖直平移点P3则固定翼型弦长而改变弯曲角（如翼型B至C）。可见翼型弯曲角与弦长在几何上互不干涉，且能唯一确定单圆弧翼型形状。因此，翼型的几何形状，在定义范围内连续且不存在形状“空缺”，这保证了全局最优解在翼型形状方面的合理性。

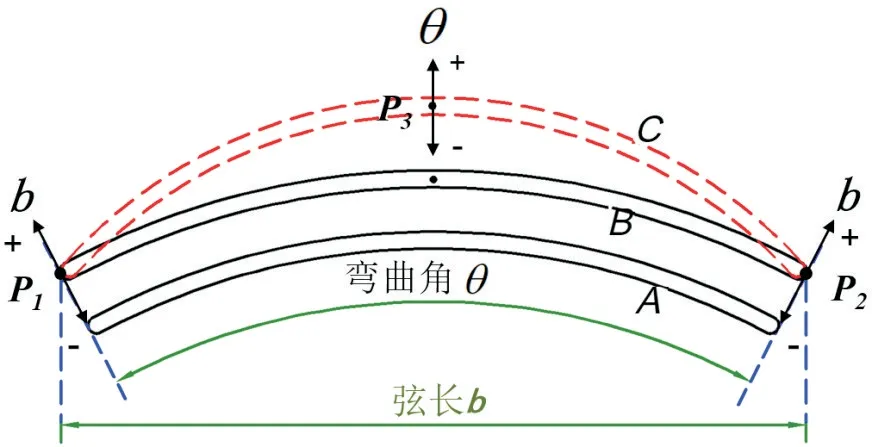
图3 翼型形状控制方式Fig.3 Airfoil shape control

叶片安装角βb确定了叶片相对于轴线的安装角度，不同叶片安装角的旋转中心为翼型弦长的0.45 倍处。轴向间隙δa定义为叶轮轮毂与后导叶轮毂间距，轴向间隙的取值有一定范围，过大或过小都会增加流动损失[8]。由于本模型电机置于后导叶轮毂内部且电机轴直连叶轮，电机轴的弯曲应力的限制使轴向间隙只能在小范围内取值。设计参数的范围在所研究模型机的基础上设定合适上下限，具体见表1。

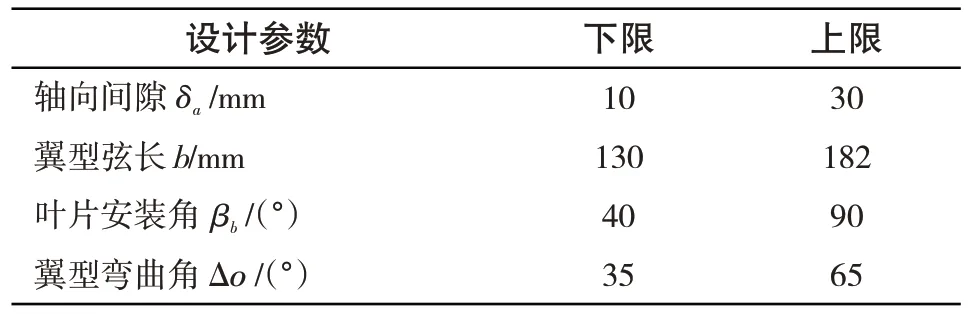
表1 设计参数范围Tab.1 Design parameter range

2 优化技术及流程

2.1 优化流程

风机后导叶的优化流程如图4 所示。首先通过最优拉丁方超立方（Optimal Latin Hypercube）试验设计将设计参数划分为44 组，对其分别进行CFD 仿真计算得到相应性能参数，从而获得44 组样本空间数据；通过Isight平台对样本空间数据建立起一个初级的EBF神经网络模型，然后将其融合进多岛遗传算法中，以风机全压Pt及全压效率ηt为优化目标进行寻优；算法获得的最优解通过CFD仿真计算进行性能验证。若结果不满足结束条件则将最优解的设计参数与相应仿真结果作为新一组样本加入样本空间，重新建立新的EBF 神经网络模型再次使用MIGA寻优，直到满足结束条件。

图4 优化流程框图Fig.4 Chart of optimization process

结束条件规定了最优解的预测值和计算值的误差范围，并体现了最优解的合理性：

其中，下标cal 表示仿真计算值；pre 表示预测值；olhbest表示最优拉丁超立方试验的最优解。

2.2 EBF神经网络模型

椭球基（EBF）神经网络模型具有良好的综合性能，对比BP 网络大大加快了训练速度和网络适应性；对比RBF 网络则对输入空间的划分更准确和快速[9]，近似预测的准确性有所提升。

为了绕过大量的仿真计算时间，在遗传算法中融入椭球基神经网络模型。基于最优拉丁超立方试验设计的44 组样本训练而得的EBF 神经网络，通过交叉验证的误差分析，其全压与效率的R2都大于0.97，因此得到的神经网络拟合度较好，即建立的EBF神经网络模型能较准确预测设计参数和优化目标之间的响应关系。

2.3 多岛遗传算法寻优

多岛遗传算法采取多岛策略，很大程度上保证了最优解的全局性。通过该算法多代的交叉、变异、遗传等操作，寻找能够较好地匹配叶轮工作的一组设计参数（b，θ，βb，δa），以提高风机整机性能参数。由于MIGA 将多目标转化为单个内置目标函数Objective进行适应度评价，且全压和效率量级不同，因此调整全压的SF（Scale Factor）值将两者置于同量级。SF对目标函数Objective的影响为：

其中，WF为权重因子。

视效率和全压同等重要，因此保持WF默认等于1.0。基于最优拉丁超立方试验设计下的44 组样本，SFP按式（4）取值为8.28；默认SFη=1。

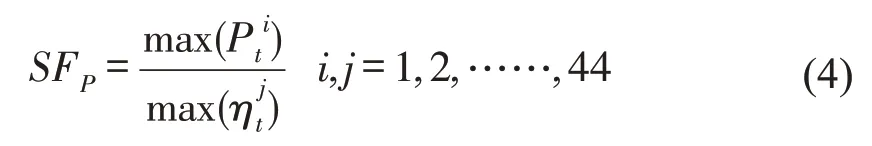
设置多岛遗传算法的种群数50，迭代数60，岛数3，交叉概率0.9，并选择最大化全压、效率为目标，同时约束效率高于70%，全压高于600Pa。

3 优化结果及其分析

3.1 优化参数分析比较

原型机与多岛遗传算法优化的风机后导叶参数如表2 所示，叶片安装角取值变大而弯曲角变小，表明优化的后导叶翼弦与轴向夹角减小，翼型弦长有所减小，如图5所示。与原型机相比，导叶优化后在风机最大流量工况下的全压效率略微降低，而全压提高6.73%。优化结果也一定程度证实了单级轴流风机后导叶安装角主要影响风压的结论[10]。

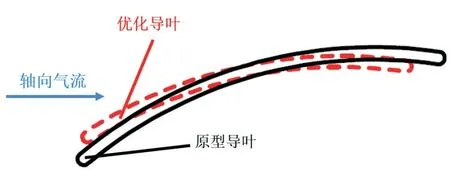
图5 优化前后翼型Fig.5 Airfoil shape before and after optimization

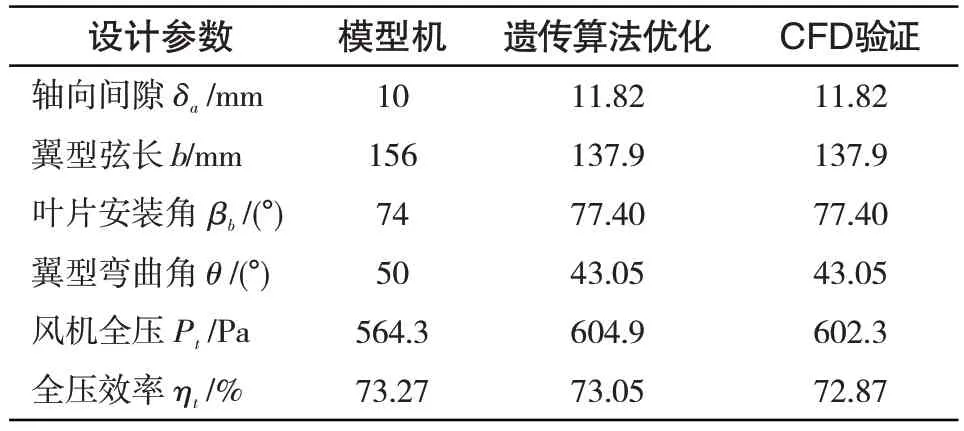
表2 模型机与优化结果对比Tab.2 Comparison of model fan and optimized results

图6是44组最优拉丁超立方试验设计结果的全压Pareto 图，反映了各设计参数对全压影响程度的百分比。由Pareto 图可看出叶片安装角对风机全压有重要影响，翼型弯曲角和弦长对风机全压的影响相对较小且为负效应。而由于电机设置方式的限制，本文所研究的小范围的轴向间隙变化对风机全压几乎无影响。

图6 全压的Pareto图Fig.6 Pareto graph of total pressure

3.2 流场分析

从设计参数的优化结果来看，后导叶安装角增大而弯曲角减小明显，图7显示了导叶不同叶高处翼型周围的流动情况，一定程度说明了这两个设计参数变化所带来的影响。

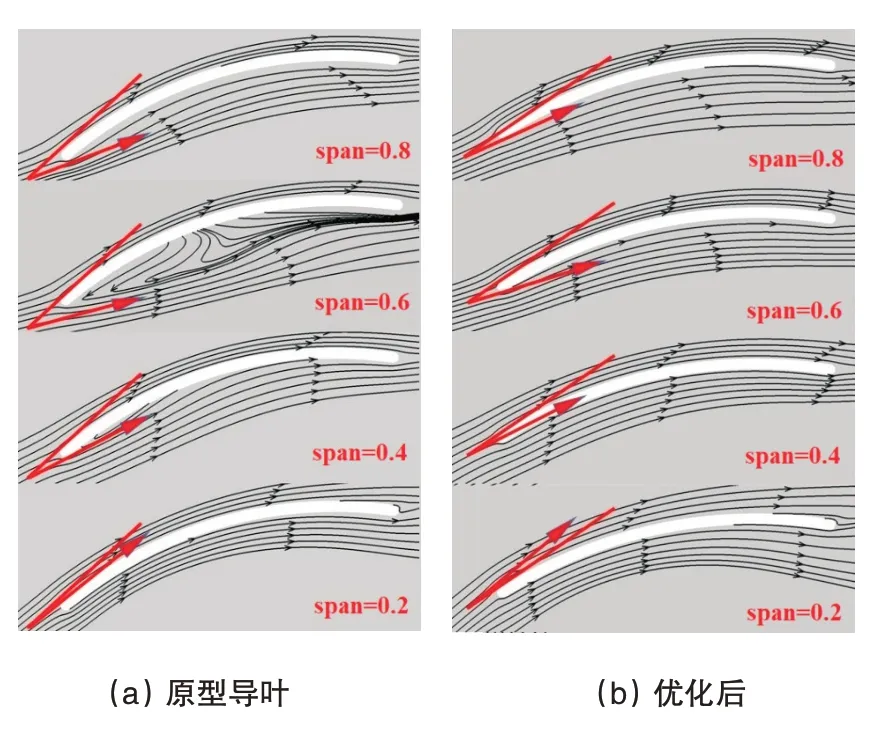
图7 后导叶不同叶高截面的流动情况Fig.7 Flow characteristics of different blade height cross sections of rear guide vanes

原型机在近轮毂（Span=0.2）处气流负攻角最小，拥有理想的流线；约在Span=0.6 处，气流负攻角达到最大，因此产生了翼型压力面的回流现象，造成巨大流动损失。在负攻角稍小的Span=0.4 处，则出现初始的微小回流。优化后安装角的增大使得各叶高截面的翼型进口气流的负攻角均减小，有效遏制了回流的发生。翼型弯曲角的减小放缓了导叶区域气体流向改变的速度，一方面能够协助抑制后导叶压力面的回流；另一方面，即使优化后导叶近轮毂处气流出现了微小正攻角，其吸力面后部仍未出现流动分离现象。因此优化后的导叶在不同叶高处均具有较为理想的流动，后导叶引起的流动损失被降到了较低的水平。

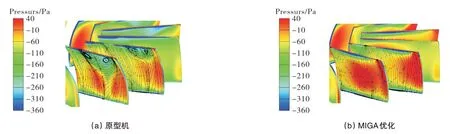
图8 后导叶压力面静压与流线Fig.8 Static pressure and streamline of back guide vane pressure surface

图8 显示了后导叶压力面上的静压和流线。从流线可明显观察到原型机的导叶压力面靠近前缘位置存在一对涡。这对涡分布于上述回流最严重的叶高截面两侧，其原因正是导叶展向无扭转而压力面回流现象只存在于一小部分叶高（Span=0.6）处，导致回流区两侧叶高处的正常流向气流转向该区域而使气体拥有了径向速度。近涡心气流随回流返回导叶前缘，便形成了涡，并在压力面涡存在的区域形成“静压谷”；远涡心气流则带有一定径向速度冲击回流截面一侧，造成气流在导叶一定叶高堆积流出。一方面，涡的存在引起涡流损失；另一方面，涡旋减小了导叶压力面作用面积——这一点从压力面高静压区域的面积变化上也可看出，使导叶出口气体存在较大周向及径向速度分量。

经MIGA优化的后导叶压力面流动情况得到改善，涡旋的消除使得压力面作用面积得到充分利用，并极大程度减少了后导叶带来的压力损失，风机全压得以升高。因此优化后的导叶更加匹配风机叶轮的运转。

5 结论

1）通过最优拉丁超立方试验设计下的44组样本点建立的EBF 神经网络模型，可以准确预测轴流风机后导叶设计参数与优化目标之间的响应关系。并使用多岛遗传算法获得一组后导叶的最优设计参数。

2）优化结果与原型机相比，在最大流量工况下风机全压效率变化很小，全压则提高了6.73%。后导叶叶片安装角对风机性能影响较大，优化后安装角的增大与弯曲角的减小使后导叶进口气流负攻角减小，消除了回流与涡旋的产生，降低了后导叶过流损失，改善了叶轮与导叶的匹配关系。