凹坑对风力机翼型气动性能的影响＊

王艳芬 陆华伟 郭 爽 王 龙 辛建池

（1.大连海事大学 船舶与海洋工程学院；2.大连理工大学 能源与动力学院）

0 引言

风能作为世界上重要的可再生能源之一，使得风力机发电受到越来越多的重视，叶片是风力发电系统的主要部件，其气动性能的好坏直接影响风力机发电效率的高低。研究翼型的减阻增升措施对提高翼型气动性能、增加风力及风能利用系数具有重要意义，进而获得较好的风能发电效率[1]。

风力机翼型常见的减阻方法分为主动控制技术和被动控制技术，主动控制主要包括等离子体激励[2]、附面层抽吸[3]、翼型表面吹吸气[4]等技术，被动控制包括涡流发生器[5]、前尾缘襟翼[6,7]、吸力面翼刀[8]等。凹坑作为非光画表面被动控制技术在压气机以及涡轮叶栅上的研究相对较多，目前很少有文献研究凹坑对风力机叶片气动性能的影响。现有文献中最早的关于凹坑表面的研究是Bearman和Harvey[9]在1976年对高尔夫球气动性能进行的研究，发现凹坑使得高尔夫球的阻力较光滑表面降低50%，而且在一定的雷诺数范围内均能保持较低的阻力系数。并指出凹坑内部应存在分离涡，这能够提高边界层的动能水平，进而使得边界层的转捩位置提前，提高了边界层抵抗流动分离的能力，降低了球在飞行过程中所受到的压差阻力。Rubiat Mustak[10]等通过实验验证了凹坑表面对于翼型的作用效果。研究表明，对于工作在低雷诺数下的机翼翼型，布置在机翼上表面的凹坑内部能够产生分离涡，在分离涡的作用下，边界层转捩位置会提前，边界层分离被延迟。翼型的升力系数得到提高，可工作攻角范围增大。Lake等[11]通过实验对凹坑、V型沟槽的减阻特性在一定雷诺数范围内，两种湍流度下进行了比较。研究发现，相比沟槽和拌线，凹坑实现减阻时具有更宽的雷诺数范围和自由来流湍流度，而沟槽对其分布位置要求严格，只在分离点上游才能实现减阻。

1 数值模型建立

本文的研究对象为NACA 4412 翼型，该翼型主要应用于风力机叶片的叶中和叶尖位置，最大相对弯度为4%，最大弯度的相对位置40%，最大相对厚度为12%，弦长为1000mm。

1.1 研究方法及数值计算可靠性验证

翼型前缘计算域采用半径为12.5倍弦长半圆，翼型后缘据计算域出口为20 倍弦长，翼型与计算域上下边界的距离均为12.5倍弦长选取足够大的计算域可以减小边界周围流场对翼型绕流流场的影响。边界条件定义见表1。

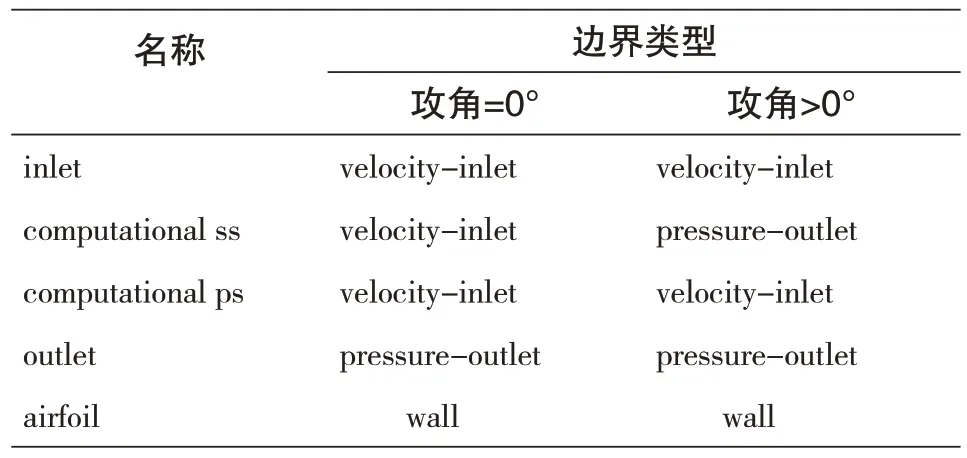
表1 边界条件设定Tab.1 Setting of boundary conditions

图1 为计算域网格示意图，采用ICEM 划分C 结构化网格，并对靠近翼型的计算域进行加密处理以适应该部位复杂的气流流动，本文设置不同的网格尺寸进行独立性检测，结果见图2。

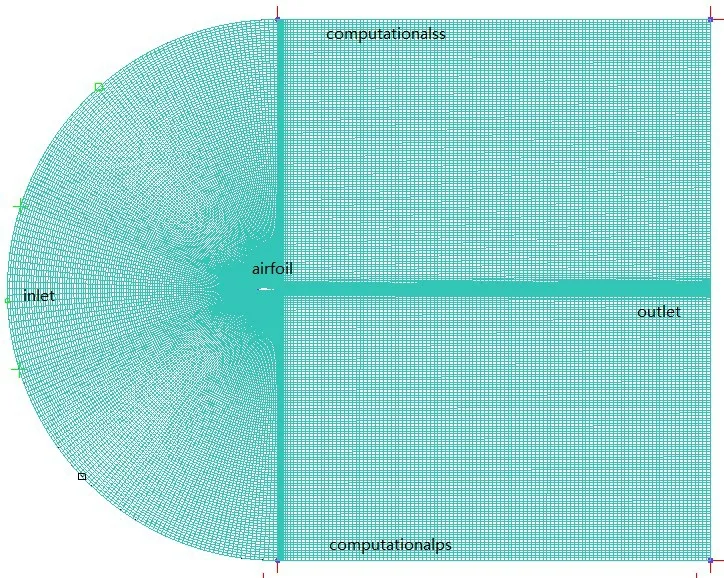
图1 计算域网格示意图Fig.1 Computational domain grid diagram

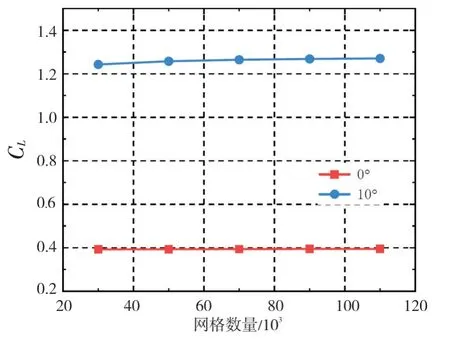
图2 网格无关性验证Fig.2 Grid independence verification

翼型周围流场采用fluent 15.0 计算，选用SIMPLE算法和SSTk-ω湍流模型进行数值求解，近壁面y+值约为1，方程采用二阶迎风格式，当计算残差小于10-5时认为迭代计算收敛。

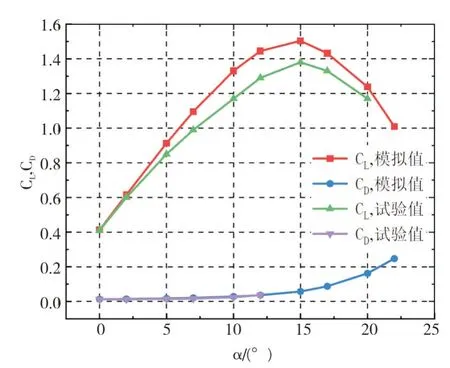
图3 升、阻力曲线对比Fig.3 Contrast of lift and resistance curves

为了验证数值计算模型的准确性，计算了NACA4412翼型在Re=6.8×105条件下的气动特性，该雷诺数与6.8×105接近，因此将结果与试验数据[12]进行对比，结果如图3所示，结果显示：升力系数和阻力系数计算结果与试验结果相差很小，基本都在10%的误差范围之内，分析原因一方面是没有考虑试验中的机械能损失，另一方面计算结果的变化趋势仍与试验结果的变化趋势一致，故判定算法可靠。

1.3 凹坑方案说明

相关文献表明将凹坑布置在吸力面合适的位置可以减小分离[13]，本文首先分别将半径R=5mm 的凹坑布置在吸力面10%～28%，32%～50%，42%～60%，60%～78%弦长（分别命名为Case1，Case2，Case3，Case4）处，然后分半径为7mm，10mm，12mm，15mm的凹坑（分别命名为Case5，Case6，Case7，Case8）布置在60%～78%弦长处，最后在60%～84%弦长处布置半径为10mm的凹坑（Case9）凹坑深宽比h/d=0.25，球形凹坑的最大截面与当地截面垂直，翼型原型命名为Ori，凹坑方案如图4所示。

图4 凹坑方案示意图Fig.4 Schematic diagram of dimple scheme

2 结果分析

采用fluent 15.0 对以上8 种凹坑方案进行数值模拟，分析凹坑对叶片气动性能的影响，计算条件为：雷诺数Re=6.8×105，攻角α=0°～30°，风速为v=10m/s。

2.1 凹坑对翼型升阻力特性的影响

翼型的升阻力特性可以用升力系数和阻力系数随攻角的变化曲线表示，翼型受到的合力可以分解为升力和阻力，升力方向垂直于流速方向，阻力方向平行于流速方向，来流流过翼型表面时，上翼面速度大，下翼面速度小，因此上翼面压强大，下翼面压强小从而因压差形成升力[14]。升力系数和阻力系数的公式为：

式中，ρ为来流密度；U∞为来流速度；S为翼型面积，二维时可用弦长代替。

图5（a），图6（a）为改变凹坑位置时升力系数和阻力系数随攻角的变化曲线，从图5（a）中可以看出随着攻角增大升力系数呈线性增加，当攻角达到一定角度时，升力系数开始减小，翼型失速；原型叶片在15°左右时，升力系数达到最大，带凹坑叶片的最大升力系数都小于原型，但在大攻角下，升力系数相对于原型叶片来说有一定的改善作用，此时翼型已经进入失速状态，从图中可以看出，Case4 在25°～30°升力系数比原型叶片升力系数大，并在27°时比原型增加了4%。由图6（a）可知，阻力系数随攻角的增加而增加，大攻角下带凹坑叶片阻力系数普遍较原型叶片大但差距不大，Case4在25°时阻力系数降低了1.8%。

图5（b），图6（b）为改变凹坑半径大小和排数时升力系数和阻力系数随攻角的变化曲线，从图5（b）可以看出，大攻角下带凹坑叶片升力系数比原型叶片大，并随着凹坑半径的增加升力系数先增加后减小，当半径为10mm（即Case6）时，升力系数达到最大，并在27°时升力系数增加了4.9%，而增加一排凹坑（即Case9）后升力系数相对于原型增加了6.9%。由图6（b）可知，在攻角为25°～27°时，带凹坑叶片阻力系数较原型叶片几乎吻合。

从图中可以看出，以上各凹坑方案中，Case2、Case4、Case6、Case9 升力系数提高较明显，其中Case4、Case6 位置相同，因此接下来，本文主要讨论Case2、Case6、Case9三个方案。

图5 升力系数随攻角的变化曲线Fig.5 The change curve of lift coefficient with the angle of attack

图6 阻力系数随攻角的变化曲线Fig.6 The change curve of drag coefficient with the angle of attack

2.2 凹坑对流场分布的影响

图7、图8 和图9 分别为攻角为12°、25°和30°时Case2、Case6 和Case9 与原型流场分布对比图，图10 为攻角为12°各方案的翼型尾迹流线图，从图7和图10中可以看出，在攻角为12°时翼型上翼缘发生了轻微流动分离，与原型相比三种方案产生了更大的分离涡，小攻角分离稍微小一些，加上凹坑扰动会导致涡的强度变大，分离增加。并随着凹坑位置向尾缘移动、凹坑排数的增加，分离区增加，升力系数降低。从图8 和图9 可以看出，与原型叶片相比三种方案都能使分离减小，大攻角分离很大，凹坑分离涡使得大涡发生耗散，分离减小。并且随着凹坑位置向尾缘移动、凹坑排数的增加，分离区减小，升力系数增加。

图7 攻角α=12°时翼型周围流速分布图Fig.7 Velocity profile around airfoil at α=12°

图8 攻角α=25°时翼型周围流速分布图Fig.8 Velocity profile around airfoil at α=25°

图9 攻角α=30°时翼型周围流速分布图Fig.9 Velocity profile around airfoil at α=30°

图10 攻角α=12°时翼型尾缘流线图Fig.10 Flow diagram at trailing edge of airfoil at α=12°

2.3 凹坑对压力系数分布的影响

将凹坑布置在风力机叶片上必然会改变叶片表面的压力系数，压力系数公式为：

式中，p为翼型表面某点的绝对压力；p∞为自由来流的绝对压力；ρ为大气密度；U为来流风速。

凹坑对叶片压力系数的影响如图11，曲线的包络面积表征翼型的加载能力[15]，吸力面的压力越小，压力面的压力越大，翼型的加载能力越好，升力系数越大，从图中可以看出，在攻角为12°时，Case2、Case6、Case9的压力面压力系数降低，吸力面压力系数增加，在0.75弦长后斜率变小，使得压力系数较原型降低，但其降低的程度不足以抵消0.75弦长前增加的程度，因此翼型的升力系数降低。当攻角大于25°时，三种方案吸力面压力系数都有降低，在0.05弦长附近变化较明显，且随着凹坑位置的向尾缘移动，凹坑半径、排数的增加，吸力面压力系数降低的越明显，翼型升力系数增加的越明显。

图11 压力系数分布曲线Fig.11 Pressure coefficient distribution curve

3 结论

本文将凹坑布置在NACA4412 风力机叶片上，在Re=6.8×105时通过改变凹坑位置大小等，分析其对叶片气动性能的影响，可以得出以下结论：

1）在风力机叶片上布置合适的凹坑，能减小分离，进而增加升力系数，风力机升力系数随攻角的增加先增加后减小。

2）大攻角下，合适的凹坑能够减小分离，将凹坑布置在叶片尾缘附近分离涡相对于原型更小，随着凹坑半径的增加，减小流动分离的效果先增加后减小，在半径为10mm 时控制效果最好。当攻角大于25°时，将半径为10mm 的凹坑布置在60%～84%弦长处，可使升力系数增加6.9%。

3）大攻角下，在叶片吸力面布置合适的凹坑能够使吸力面压力系数降低，从而使叶片升力系数升高。