大桥桥塔温度及温度效应分析

【摘 要】为研究研究混凝土桥塔在高原大温差、强日照环境下由温度应力引起的混凝土结构表面开裂问题，文章以规划中某大桥为背景进行分析。对于西藏地区极端气候（环境温度变化范围为-10～30 ℃）条件下的桥塔节段的受力特性进行了研究，模拟在24小时内历经降温-升温-降温过程，在日照辐射、热传递、对流的作用下，对比分析了不同边界条件、是否施加荷载和不同截面形式的桥塔结构混凝土层的温度场分析、应力场分析、拉伸损伤以等不同因素。结果表明：（1）改进截面方案中混凝土块倒角使混凝土块周围力线过渡平缓，有利于减少应力集中;（2）轴向荷载有利于减缓核心混凝土的开裂;（3）布置加劲肋有利于减缓核心混凝土的开裂;（4）此添加岩棉板有利于减缓核心混凝土的开裂。

【关键词】日照辐射; 热传递; 不同截面形式的桥塔结构; 高原大温差; 强日照

【中图分类号】

U441+.5【文献标志码】A

高原地区呈海拔高、环境湿度小、日温差及季节性温差大等特点。对西部高原地区的多个混凝土工程实地调研发现，部分结构在服役中后期开裂严重，而非在建成初期，并且其开裂规律与平原地区有较大差别[1]。高原特殊环境对混凝土结构的力学性能和耐久性具有显著的劣化效应。由于干燥、大风等因素，塔柱易在结构表面产生微裂缝，随后在温度变化、冻融循环、酸碱腐蚀、超重行车等外界作用下，裂缝进一步扩展贯通至失效。而周期性变化的大气温差，强烈日照等非线性温度荷载使结构体内产生的温度次应力，往往超过结构恒载、活载及其它作用产生的应力，是致使桥塔表面开裂的重要因素[2]。国内外均有因温度作用引起混凝土桥梁失效的相关报道[3-5]。当桥塔表层开裂部位积水并经历反复冻融，导致内部钢筋锈蚀，进一步加速开裂过程，显著降低结构的承载力、耐久性与服役质量，且加固困难，亟需研究防止高原环境下混凝土桥塔开裂的有效措施。

王鹏等[6]研究了某斜拉桥混凝土桥塔降温作用下的早期温度收缩裂缝特性，结果表明：当环境降温与水化热同时作用时，混凝土桥塔开裂的可能性会大大提高。黄维树等[7]对温度效应计算的方法进行介绍，然后以有限元分析方法，开展温度仿真分析以及热力耦合分析，最后分别对各塔节的开裂原因进行总结分析。向学建等[8]针对高原地区冬季条件下箱梁温度场的边界条件的确定进行了较为深入的研究。张宁等[9]对高原高寒地区四季典型气候特点下桥塔的温度场进行详尽分析，并对桥塔四季的温度效应进行精细化计算。

目前，国内外学者对高原地带下极端温差下混凝土的开裂的影响进行的还不够全面，对桥塔温度场研究不够多。此处主要研究混凝土桥塔在高原大温差、强日照环境下由温度应力引起的混凝土结构表面开裂问题。虽然桥塔锚固区受较大集中力影响，使塔柱锚固区成为裂缝的多发区域，但本次模拟主要考虑该桥塔处于特殊气候环境，荷载及施工技术对于混凝土开裂问题成为次要影响因素。本文以规划中某大桥为背景，基于有限元软件建立桥塔节段三维有限元模型，对不同截面形式的桥塔温度场及温度应力场进行研究。

1 工程背景

大桥桥长1 200 m，桥高610 m，为双线铁路桥，线间距为7.5 m。大桥为主跨1 000 m钢桁梁悬索桥方案，主梁孔跨布置为（120+1000+80） m。主缆矢跨比为1/9，全桥采用两根主缆，主缆孔跨布置为（260+1000+260） m。主梁采用钢桁梁，主塔暂定采用H型钢筋混凝土结构，基础采用群桩基础，锚碇采用隧道锚。全桥土建工期约72个月。

2 有限元模型和计算条件

2.1 有限元模型

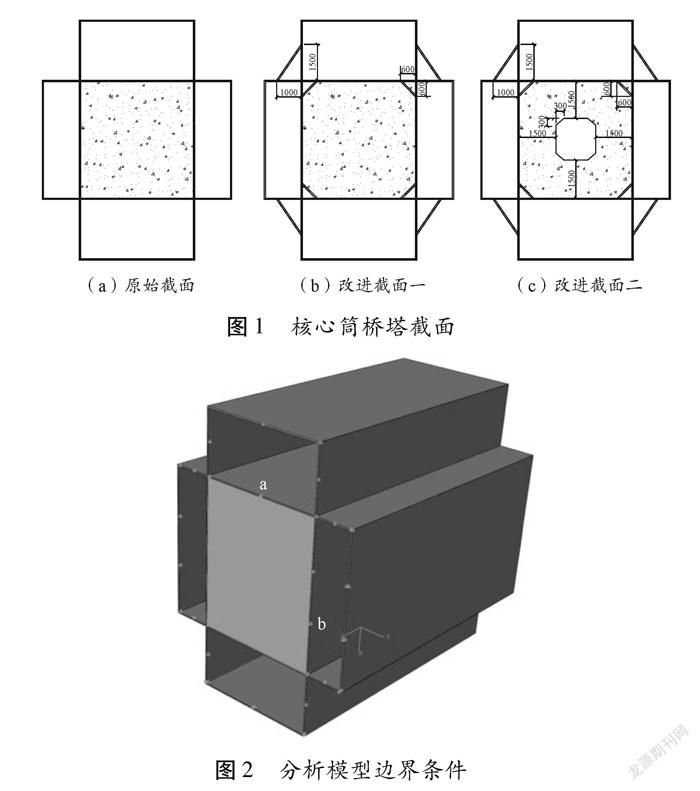
首先对桥塔节段进行三维瞬态温度场分析，再将温度场作为温度荷载加载于模型，以实现热力耦合分析。在ABAQUS软件中，三维瞬态温度场分析采用DCC3D8单元模拟。应力场分析中采用实体元C3D8R单元进行模拟，为提高计算效率，分析中暂不考虑组合结构各部分之间滑移的影响，接触面均采用绑定接触模拟。我们该次分析主要研究核心筒组合桥塔，核心筒桥塔三种不同截面（原始截面和两种改进截面）形式如图1所示。为使桥塔节段受力尽可能接近实际状态，限制桥塔节段底面x-y面的z方向位移，在边界a再施加y方向约束以及限制边界b的x方向位移，如图2所示。

2.2 温度边界条件

桥塔日照温度场数值模拟，其目的是得到混凝土结构温度场，从而分析出最不利的温度荷载。影响结构温度场的因素，从能量来源方面，可以分为三类，即太阳直接辐射，结构与空气的热对流以及结构本身与周围环境以长波辐射形式的热交换。

2.2.1 太阳直接辐射qs

太阳是地球能量的主要来源，同时也是结构温度场变化的源头。太阳辐射将使得大气温度在昼夜之间产生明显差异，呈现日周期性变化。因此模型中通常不能忽略日升温及降温过程中的太阳辐射值。根据文献选取太阳辐射日变化过程的近似函数[10]。

式中：q0为正午最大辐射，q0=0.131 mQ;m=12/c;Q为日太阳辐射总量，夏季取26×106 J/m2，冬季取20×106 J/m2;c为实际有效日照时间，夏季取12 h，冬季取9 h;夏季最大辐射取800 W/m2，冬季取400 W/m2，具体取值可根据实际插值选取。

2.2.2 辐射辐射换热qr

根据斯蒂芬-玻尔兹曼定律和基尔霍夫定律，可以得到结构辐射如下计算式[11-12]：

式中：Ta为环境温度，hr为辐射换热系数，Tv为物体表面温度，辐射换热系数hr可由下式计算[12]：

式中：ε为物体表面的热辐射率;Cb为黑体辐射系数，值为5.67 W/（m2·K）。

采用上式計算辐射换热系数较为复杂，本次数值模拟采用下式近似计算：

2.2.3 对流换热qc

对流换热通常指结构表面与周围空气的换热。当结构与空气温度不同时，结构表面与流体之间会发生热量交换，即对流换热。对流换热按照形成的原因，可以分为自然对流和受迫对流。在实际桥梁工程中，只涉及自然对流。

对流换热可由牛顿对流换热定理表示为[14]

式中，hc为对流换热系数，单位W/（m2·K）;Tv为桥塔表面温度;Ta为结构周围环境温度，考虑到实际情况，即为结构所在地大气温度。

2.2.4 环境温度

结构周围环境温度取值，可以根据实际情况，实际测量当地空气温度，也可以根据当地气象数据，通过每日最高气温Tmax，最低气温Tmin，进行拟合的气温曲线来取值，可表示为：

式中：Ta为t时刻环境的拟合气温，Tmax为日最高气温，Tmin为日最高气温，t为时间，0≤t<24。

根据怒江大桥实际所处桥址——西藏自治区昌都市八宿县气象观测显示。极端年最高高温为33.4 ℃，极端低温为-16.9 ℃，年均溫度为10.4 ℃。但鉴于缺乏最不利日气温观测资料，本次数值模拟采用每日最不利气温拟合的曲线来取值分析。采用Tmax=30℃，Tmin=-10℃。本次模拟环境温度按照日气温变化曲线设置，如图3所示。

本次分析根据拟合的温度曲线，模拟桥塔处于极端气候条件下在24 h内经历降温—升温—降温过程，日照辐射强度按照式（1）作为模型参数输入进行施加荷载。由于无法确切知道某一时刻结构所有部分的温度，本次模型模拟进行一定简化，在模型中假定某一合理初始状态，通过周期性热交换消除该初始状态对于温度场的影响，以桥塔外部边界温度变化模拟环境温度变化，从而能够较为准确地模拟实际情况。假设模型初始温度为最低气温0：00时刻的温度值2.35 ℃，设置模型外边界与环境温度共同变化，以此消除简单设置的初始温度边界对于模型温度场计算造成的误差。

3 计算结果和分析

3.1 线性计算

先不考虑混凝土的材料非线性和几何非线性，以此来对比不同截面在一天相同温差下的混凝土的温度场和应力场分布。

3.1.1 温度场分析

基于ABAQUS有限元模型计算了桥塔节段的节点温度场分布，截面形式节点温度场分布如图4所示。当结构处于模拟的条件下24 h之后，①原始截面：内外侧温差达到了9.89 ℃，截面最高温度位于核心筒四个倒角处，容易出现应力集中。最大温度为12.24 ℃; ②改进截面一：内外侧温差达到了9.69 ℃，截面最高温度位于核心筒四个倒角处，容易出现应力集中。最大温度为12.04 ℃;③改进截面二：内外侧温差达到了6.16 ℃，核心筒四周温度均较高。最大温度为8.51 ℃。

3.1.2 应力场分析

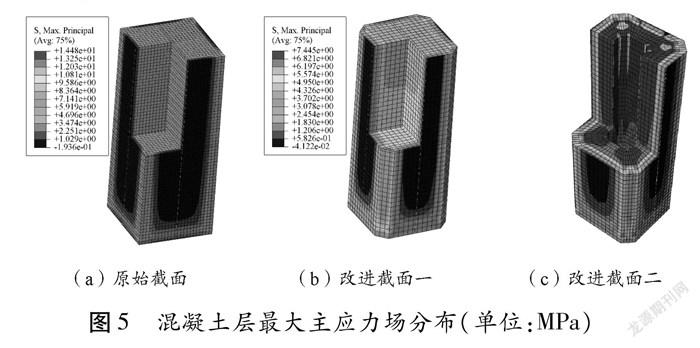
对于核心筒组合桥塔上横梁附近节段，截面形式节点应力场分布如图5所示。①原始截面：混凝土层最大主拉应力为14.48 MPa，位于核心混凝土截面四角;②改进截面一：混凝土层最大主拉应力为7.45 MPa，位于核心混凝土截面四角;③改进截面二：混凝土层最大主拉应力为6.53 MPa，位于核心混凝土截面四角。

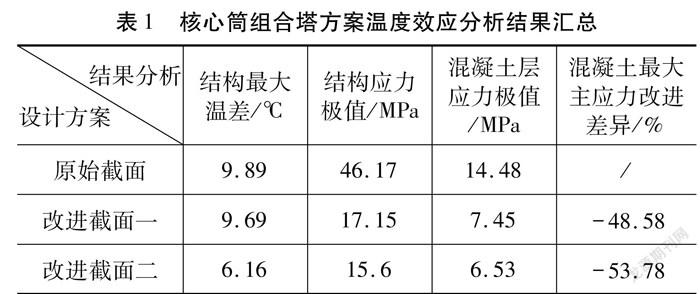
由表1可得，以上改进设计方案均有一定的改进效果，改进方案二的作用最显著，降低了53.78 %，但混凝土最大主应力仍然达到6.53 MPa，这是因为前面采用的是线性计算，未考虑混凝土的非线性，所以仍需进一步再设计方案或计算方法上改进。

3.2 非线性计算

接下来考虑混凝土的材料非线性和几何非线性，采用非线性计算进行分析。统一采用对改进截面一不同改进方案进行分析。

3.2.1 温度场分析

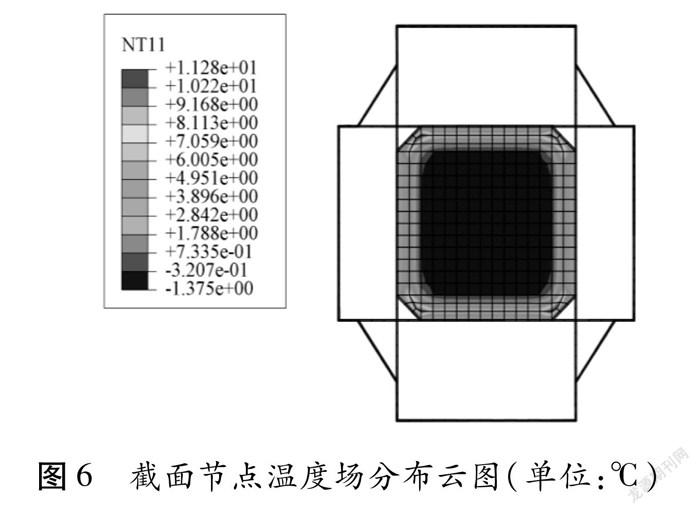
（1）对截面不采用任何改进措施基于ABAQUS有限元模型计算了桥塔节段的节点温度场分布，改进截面一形式节点温度场分布如图6所示。当结构处于模拟的条件下24 h之后，内外侧温差达到了12.66 ℃，截面最高温度位于核心筒四个倒角处，容易出现应力集中。最大温度为11.28 ℃，内部仍为负温。

（2）在竖向施加截面轴力，轴力大小采用恒载作用下的截面内力，大小F=366 866.59 kN ，荷载施加在竖向顶面。

基于ABAQUS有限元模型计算了桥塔节段的节点温度场分布，改进截面一形式节点温度场分布如图7所示。当结构处于模拟的条件下24 h之后，改进截面一：内外侧温差达到了9.70 ℃，截面最高温度位于核心筒四个倒角处，容易出现应力集中。最大温度为9.70 ℃。

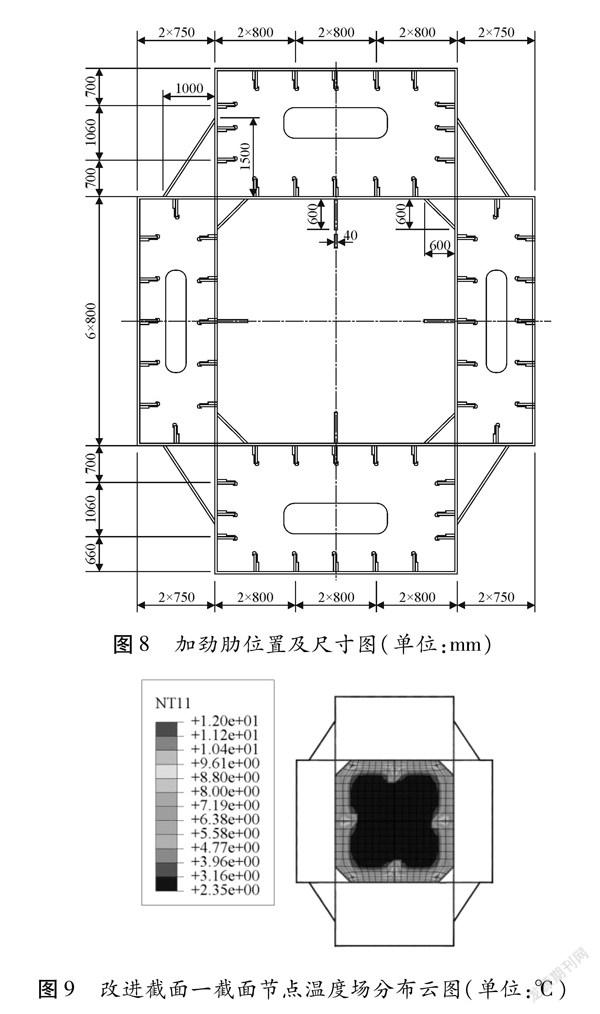
（3）设置加劲肋，在中间筒钢板中间位置设置一道加劲肋，加劲肋厚度40 mm，宽度取计算得温度效应在混凝土中的影响深度600 mm，加劲肋的尺寸和位置见图8。

于ABAQUS有限元模型计算了桥塔节段的节点温度场分布，改进截面一形式节点温度场分布如图9所示。当结构处于模拟的条件下24 h之后，内外侧温差达到9.65 ℃，截面最高温度位于核心筒四个倒角处，容易出现应力集中。最大温度为12 ℃。

（4）同时设置加劲肋和施加轴向荷载，参数同上述一致。

于ABAQUS有限元模型计算了桥塔节段的节点温度场分布，改进截面一形式节点温度场分布如图10所示。当结构处于模拟的条件下24 h之后，改进截面一：内外侧温差达到了9.65 ℃，截面最高温度位于核心筒四个倒角处，容易出现应力集中。最大温度为12 ℃。

（5）加设岩棉板。截面类型在改进方案一截面基础上改进加设岩棉板，因岩棉板纤维细长柔韧，渣球含量低，导热系数低，具有极佳的保温效果，有望减小温度效应的影响。岩棉厚度h分别取10 cm、15 cm、20 cm、25 cm。改进方案一和计算截面如图11所示。

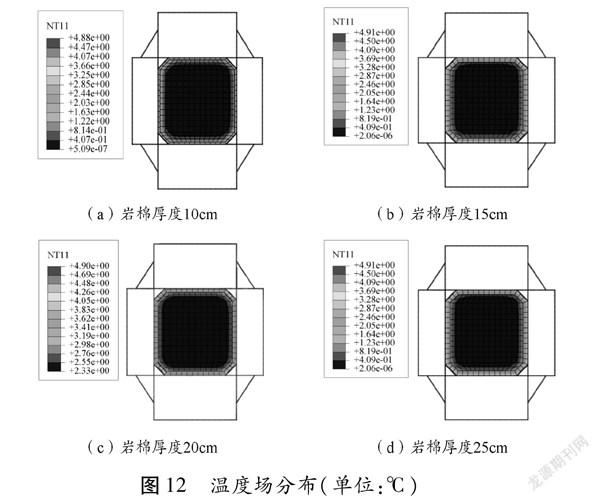
于ABAQUS有限元模型计算了桥塔节段的节点温度场分布，改进截面一在四种不同岩棉厚度下的节点温度场分布如图12所示。当结构处于模拟的条件下24 h之后，图12（a）岩棉厚度10 cm：截面最高温度位于核心筒四个倒角处，容易出现应力集中。最大温度为4.92 ℃;图12（b）岩棉厚度15 cm：截面最高温度位于核心筒四个倒角处，容易出现应力集中。最大温度为4.91 ℃;图12（c）岩棉厚度20 cm：截面最高温度位于核心筒四个倒角处，容易出现应力集中，最大温度为4.90 ℃;图12（d）岩棉厚度25 cm：截面最高温度位于核心筒四个倒角处，容易出现应力集中，最大温度为4.91 ℃。

由上述采取的不同措施对比可知，考虑在钢板和混凝土间添加岩棉板后，岩棉板保温效果极为显著，可作为考虑选项之一。

3.2.2 应力场分析

（1）对截面不采用任何改进措施。混凝土层最大主拉应力为2.89 MPa，位于核心混凝土截面四角（图13）。

（2）在竖向施加截面轴力，数值同上所述。混凝土层最大主拉应力为2.30 MPa，位于核心混凝土截面四角（图14）。

（3）设置加劲肋，尺寸如上所述。混凝土层最大主拉应力为2.69 MPa，位于核心混凝土截面四角（图15）。

（4）同时设置加劲肋和施加轴向荷载，参数同上述一致。混凝土层最大主拉应力为2.30MPa，位于核心混凝土截面四边中部（图16）。

（5）加设岩棉板。图17（a）岩棉厚度10 cm：混凝土层最大主拉应力为0.484 MPa，位于核心混凝土截面四个倒角处;图17（b）岩棉厚度15 cm：混凝土层最大主拉应力为0.919 MPa，位于核心混凝土截面四个倒角处;图17（c）岩棉厚度20 cm：混凝土层最大主拉应力为0.787 MPa，位于核心混凝土截面四个倒角处;图17（d）岩棉厚度25 cm：混凝土层最大主拉应力为0.683 MPa，位于核心混凝土截面四个倒角处。

由上述采取的不同措施对比可知，设置加劲肋、施加轴向荷载、加设岩棉板皆可降低混凝土的应力水平，但相比较而言加设岩棉板时混凝土应力水平时最低的，计算结果收敛。

3.2.3 混凝土拉伸损伤

（1）对截面不采用任何改进措施。混凝土最大拉伸损伤为0.946，位于核心混凝土中间部分（图18）。

（2）在竖向施加截面轴力，数值同上所述。混凝土最大拉伸损伤为0.991，位于核心混凝土截面四角（图19）。

（3）设置加劲肋，尺寸如上所述。混凝土最大拉伸损伤为0.998，位于核心混凝土截面四角（图20）。

（4）同时设置加劲肋和施加轴向荷载，参数同上述一致（图21）。

（5）加设岩棉板。加设岩棉板时，混凝土没有拉伸损伤。

由上述采取的不同措施对比可知，加设岩棉板没有混凝土损伤，加设加劲肋、施加轴向荷载皆会增大混凝土的拉伸损伤。混凝土最大拉伸损伤为0.998，位于核心混凝土截面四角。

4 结论

（1）改进截面方案中混凝土块倒角：节省材料，降低工程造价;倒角使混凝土块周围力线过渡平缓，有利于减少应力集中。

（2）考虑施加轴向荷载后，核心混凝土层最大主拉应力值由2.89 MPa减小为2.30 MPa，因此轴向荷载有利于减缓核心混凝土的开裂。

（3）考虑钢箱内部布置纵向加劲肋后，核心混凝土层最大主拉应力值由2.89 MPa减小为2.69 MPa，因此布置加劲肋有利于减缓核心混凝土的开裂。

（4）考虑在钢板和混凝土间添加岩棉板后，岩棉板保温效果显著，在只考虑混凝土非线性和几何非线性时，计算结果收敛，混凝土所受到的应力未达到C50混凝土轴心抗拉强度1.89 MPa，混凝土未产生损伤。核心混凝土层最大主拉应力值由2.89 MPa减小为0.683 MPa（岩棉厚度25 cm）。因此添加岩棉板有利于减缓核心混凝土的开裂。

参考文献

[1]葛昕，葛勇，杜渊博，等. 高原气候条件下混凝土力学性能的研究[J]. 混凝土， 2020（3）： 1-4+8.

[2]赵文斌，刘建勋，张戎令，等. 强风、干寒、大温差地区混凝土箱梁早期抗裂性分析[J]. 硅酸鹽通报， 2016， 35（10）： 3253-3257+3273.

[3]Kennedy J B， Soliman M H. Temperature distribution in composite bridges[J]. Journal of Structural Engineering， 1987， 113（3）： 475-482.

[4]董旭，邓振全，李树忱，等. 大跨波形钢腹板箱梁桥日照温度场及温差效应研究[J]. 工程力学， 2017， 34（9）： 230-238.

[5]Jiang L， Yongjian L， Chenyu Z， et al. Temperature action and effect of concrete-filled steel tubular bridges： A review[J]. Journal of Traffic and Transportation Engineering （English Edition）， 2020， 7（2）：174-191.

[6]王鹏，王福敏，李琦，等.环境降温对斜拉桥混凝土主塔早期开裂影响研究[J].特种结构，2010，27（2）：66-70.

[7]黄维树，宋军.桥塔水化温度效应及开裂原因分析[J].安徽建筑，2020，27（4）：185-186.

[8]向学建，董军，刘昊苏，等.高原冬季环境下桥梁温度场各参数的确定[J].公路交通科技，2012，29（3）：58-63+85.

[9]张宁，刘永健，刘江，等，STIEMER S F.高原高寒地区H形混凝土桥塔日照温度效应[J].交通运输工程学报，2017，17（4）：66-77.

[10]严作人. 层状路面体系的温度场分析[J]. 同济大学学报， 1984 （3）： 79-88.

[11]Branco F， Mendes P， Mirambell E. Heat of hydration effects in concrete structures[J]. ACI Materials Journal， 1992， 89（2）： 139-145.

[12]Dilger W， Ghali A， Chan M， et al. Temperature stresses in composite box girder bridges[J]. Journal of Structural Engineering， 1983， 109（6）： 1460-1478.

[13]Branco F， Mendes P. Thermal actions for concrete bridge design[J]. Journal of Structural Engineering， 1993， 119（8）： 2313-2331.

[14]Elbadry M， Ghali A. Temperature variations in concrete bridges[J]. Journal of Structural Engineering， 1983， 109（10）： 2355-2374.

[15]Fu H， Ng S， Cheung M. Thermal behavior of composite bridges[J]. Journal of Structural Engineering， 1990， 116（12）： 3302-3323.

[定稿日期]2021-01-28

[作者简介]李小拥（1996～），男，在读硕士，研究方向为高性能钢与组合结构桥梁。