空间缆悬索桥纵向粘滞阻尼器减震研究

宋松科　李军歌　熊伦　刘伟

【摘 要】越来越多的悬索桥采用粘滞阻尼器以降低纵向地震位移，为确保悬索桥地震安全性具有重要意义。文章分析了粘滞阻尼器参数对紫坪铺特大桥关键部位的纵桥向地震响应的影响，对粘滞阻尼器进行了参数优化。结果表明：粘滞阻尼器可以有效减小主梁位移、支座位移，一定程度减小桥塔塔顶位移、塔底弯矩及塔底剪力，这有利于该桥梁的抗震体系;随着阻尼系数C的不断增加，桥梁各地震响应均出现了先减小后增大的趋势，表明选取阻尼器型号时有必要进行计算分析以确保阻尼器参数处于合理范围内;桥塔桩基础所处的土层或场地特性会对悬索桥两岸塔柱的内力和位移均产生一定影响;粘滞阻尼器的减震效果由阻尼系数C及速度指数α共同决定，综合考虑减震效果及阻尼器自身特性，建议阻尼器参数C=2000 kN/（m/s）α，α=0.3。

【关键词】悬索桥; 减震研究; 粘滞阻尼器; 阻尼器参数

【中图分类号】U442.5+5【文献标志码】A

1 工程概况

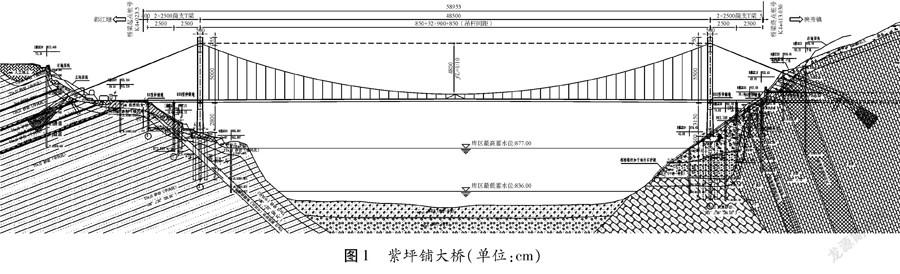
紫坪铺特大桥位于都江堰经映秀至汶川段公路上，为跨越紫坪铺水库而设。该工程区位于龙门山断裂带主中央断裂（北川—映秀断裂）与主山前断裂（江油—灌县断裂）之间，地质构造比较复杂。紫坪铺特大桥的抗震安全性成为其设计的关键问题之一。紫坪铺特大桥主桥为485 m双塔单跨钢板组合梁悬索桥，主缆分跨为125 m+485 m+125 m，两岸锚锭均为隧道锚。地震动峰值加速度0.2 g，抗震设防烈度八度，抗震设防类别为A类，抗震设防措施等级为9级。桥梁立面布置图见图1。

2 研究意义

悬索桥的主梁在纵向地震作用下并不会迫使主塔发生纵向弯曲，主塔的地震响应主要与其自身的刚度和质量分布相关，通常并不会控制结构设计。但悬索桥的主梁与主缆之间一般采用垂直吊索连接，为提高纵向约束刚度以满足抗风等纵向荷载作用下的结构性能需要，大跨度悬索桥有时会设置中央扣。这种连接构造也导致主梁的纵向地震惯性力主要由中央扣传递至主缆，若主梁在地震作用下产生较大纵向位移，也会加剧桥塔的纵向地震响应。因此，越来越多的懸索桥采用粘滞阻尼器以降低纵向地震位移。

本文以紫坪铺特大桥（空间缆大跨度悬索桥）为工程背景，分析桥梁结构特点及动力响应，在延性抗震设计的基础上，研究设置液体粘滞阻尼器后桥梁结构的地震响应，对阻尼器力学参数进行优化设计，以期为同类型桥梁的抗震设计提供有力参考。

3 粘滞阻尼器减震原理

粘滞阻尼器是由活塞、油缸、黏性液体及节流孔等组成，节流孔是比油缸截面面积小的流通通路，如图2所示。活塞具有小孔，油缸中的黏性液体一般为硅油，当活塞与油缸内往复运动时，液体从活塞一侧通过活塞上的小孔流向活塞另外一侧，从而产生阻尼力耗散结构能量。粘滞阻尼器在蠕变变形作用下，产生的阻尼力很小，接近于零;在地震作用下，活塞运动速度增大，粘滞阻尼器产生的阻尼力也会增大。粘滞阻尼器正常使用条件较严格，需要注意油压调整、漏油、灰尘侵入等问题，一旦上述问题发生，其功效可能完全失效，甚至威胁结构安全。

桥梁安装粘滞阻尼器后，粘滞阻尼器不会给结构提供刚度，因此不影响结构的基准周期，图3为粘滞阻尼器的滞回曲线示意图（速度指数为1），从中可以看到其滞回曲线非常饱满，具有较强的耗能能力，同时阻尼器在最大位移状态时阻尼力为零，在最大受力状态时位移为零，这种性能有利于减小结构的受力响应。

液体粘滞阻尼器通常采用Maxwell模型（图4）进行模拟，该模型包括阻尼特性和连接刚度两个部分，弹簧与阻尼器相互串联，与实际液体阻尼器特性相符。粘滞阻尼器是与速度相联的阻尼器，其阻尼力与速度之间的理论关系可用下式表示：

F=Cv

式中：F为粘滞阻尼器的阻尼力kN;C为阻尼系数kN/（m/s）α;v为阻尼器活塞与缸体运动的相对运动速度m/s;α为阻尼器的速度指数，桥梁抗震领域中，常用值一般取0.3～1.0。

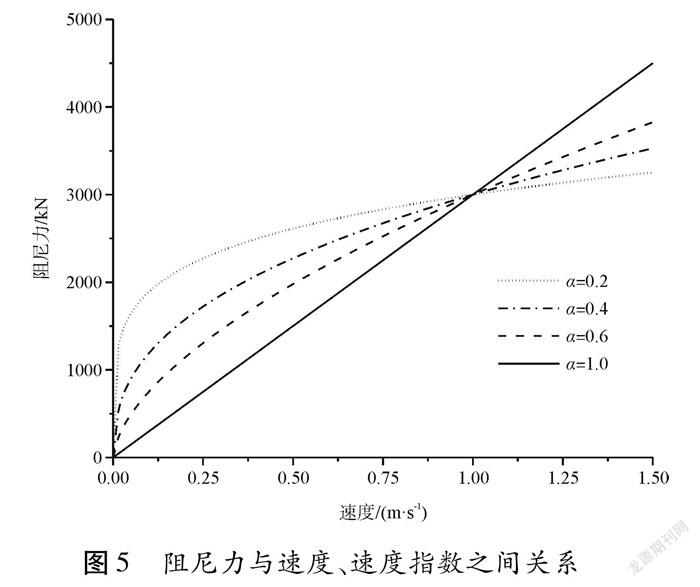
速度指数α体现粘滞阻尼器的非线性特性。当α=0时，阻尼器为纯摩擦阻尼器，当α=1时，阻尼器为线性阻尼器。图5显示了阻尼力F、速度v、速度指数α之间的关系，其中C取3 000，α≤1.0。从图中可以看出，当α<1.0时，阻尼力F随速度v增大而增大，且增速随速度增加而放缓;当速度v<1.0时，α越小，阻尼力越大;当速度v>1.0时，α越小，阻尼力越小。

粘滞阻尼器若要发挥耗能作用，需要一定的相对位移、相对速度。因此考虑将粘滞阻尼器布置在悬索桥主梁端部。当地震作用时，主梁与桥塔下横梁发生相对运动，阻尼器开始进入耗能阶段。在每个桥塔下横梁均设置一对阻尼器。

4 阻尼器优化计算工况

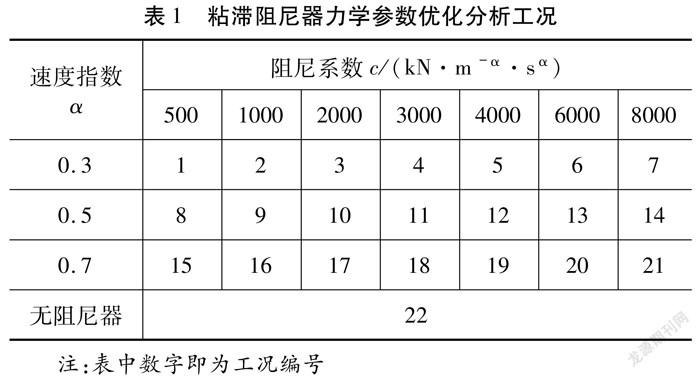
粘滞阻尼器主要力学参数为阻尼系数C和速度指数α，阻尼系数主要影响阻尼器的阻尼力，而速度指数则影响阻尼器的滞回特性。在桥梁抗震领域中，阻尼系数范围通常为500～8 000 kN/（m/s）α，α取值为0.2～1.0。因此，在对粘滞阻尼器进行参数分析时采用表1所示工况，共计22个工况。

5 地震响应规律及减震效果

5.1 位移响应比较

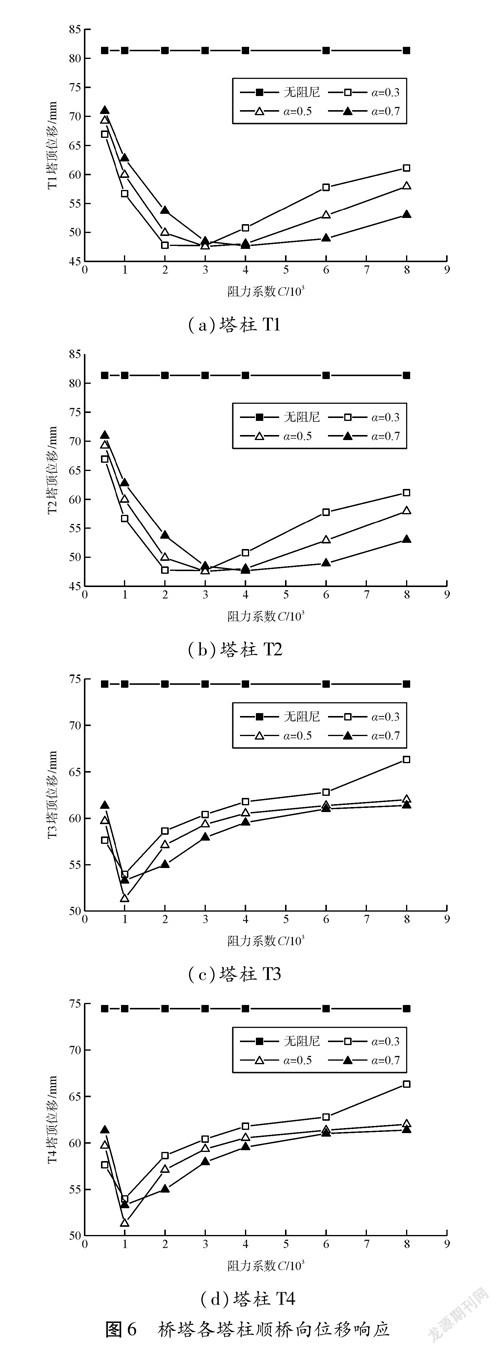
图6为桥塔各塔柱顺桥向位移响应规律，图7为左、右侧1号支座顺桥向位移响应规律，图8为左右侧梁体顺桥向梁端位移响应规律。

由上图分析可知：

（1）液体粘滞阻尼器对桥梁的桥塔、支座和梁体位移的减震效果非常显著。

（2）当阻尼器速度指数α一定时，桥塔各塔柱的塔顶纵向位移随阻尼系数C的增大出现先减小后增大的规律，表明α不宜过小或过大。

（3）阻尼器速度指数α一定时，支座和主梁纵向位移随阻尼系数C的增大而减小，当阻尼系数小于3 000时下降迅速，随后趋于稳定。

（4）当阻尼系数C小于3 000时，T1和T2塔柱顶部位移随α的减小而降低，但超过3 000后则呈相反的趋势，T3和T4塔柱则在C超过1 000后出现塔顶位移随α的减小而增大的趋势。

（5）在阻尼系数6 000范围内，梁体梁端的位移和支座位移响应均随α的减小而减小，但梁端位移在大于6 000后则呈相反的趋势。

5.2 弯矩响应比较

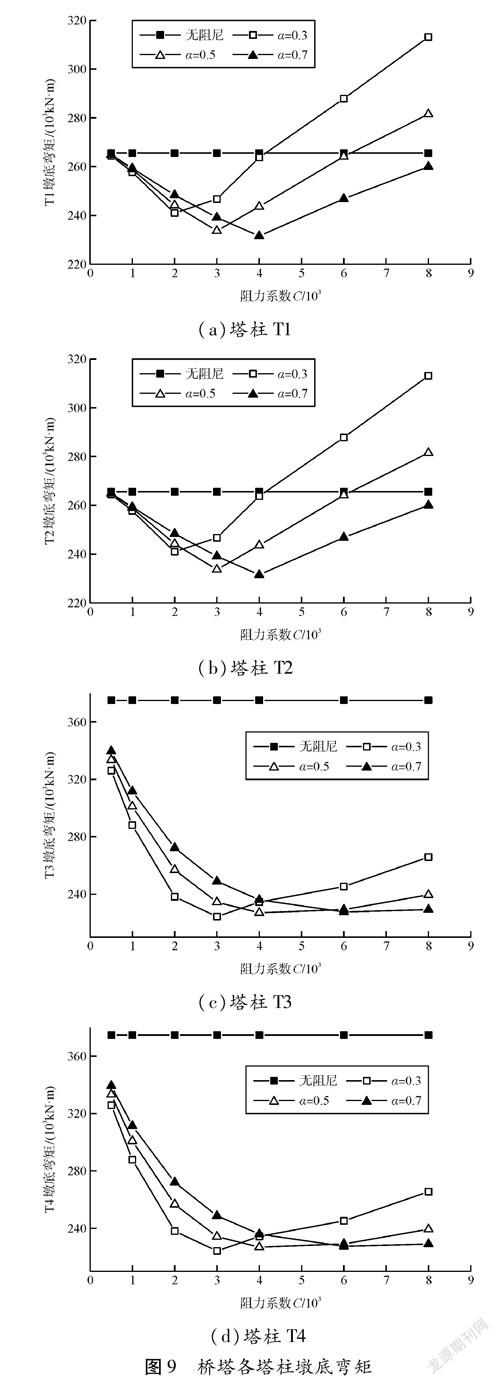
图9为桥塔各塔柱墩底弯矩圖。由图分析可知：

（1）当速度指数一定时，各塔柱的塔底弯矩随阻尼系数呈现出先减小后增大的趋势变化，在阻尼系数2 000～4 000范围内取得理想的效果。

（2）当阻尼系数超过一定值后，墩底弯矩随速度指数的增加而减小。

（3）在阻尼系数超过一定4 000，塔底的弯矩响应几乎为线性增加，表明阻尼系数过大会起到相反的作用。

5.3 剪力响应比较

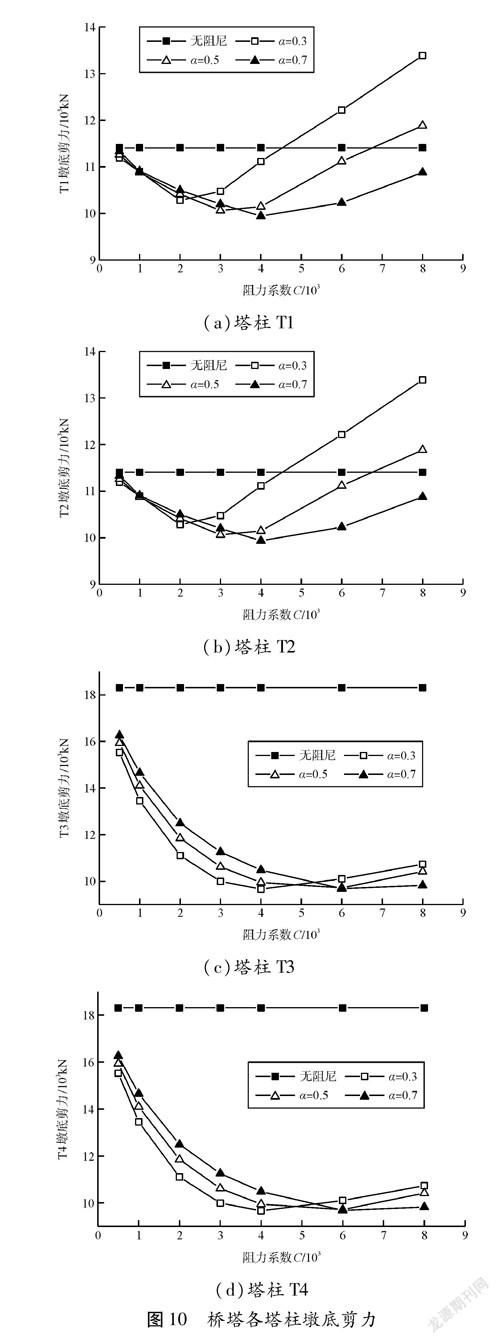
图10为桥塔各塔柱墩底剪力图，分析可知：

（1）当速度指数一定时，各塔柱的塔底剪力随阻尼系数呈现出先减小后增大的趋势变化，说明阻尼系数应取更合理的值。

（2）左侧塔柱T1、T2的最低剪力响应阻尼系数为2 000～3 000，右侧塔柱T3、T4的最低剪力响应阻尼系数为4 000～6 000，其可能的原因是两岸桩基础的土层存在较大差异，左侧为基岩场地，而右侧为覆盖土层。

（3）对于塔柱T1和T2，，阻尼系数超过3 000后，塔底的剪力随速度指数的增加而减小，而塔柱T3和T4的塔底剪力在1 000～6 000范围内随速度指数的增大而提高。

（4）阻尼系数超过一定数值后，部分工况塔底的剪力响应程线性增加，表明阻尼系数过大会起到相反的作用。

6 小结

本文分析了粘滞阻尼器参数对紫坪铺特大桥桥关键部位的纵桥向地震响应的影响，对粘滞阻尼器进行了参数优化。主要结论如下：

（1）粘滞阻尼器是一种有效的消能减震装置，可以有效减小主梁位移、支座位移，一定程度减小桥塔塔顶位移、塔底弯矩及塔底剪力，这有利于该桥梁的抗震体系。

（2）随着阻尼系数C的不断增加，桥梁各地震响应均出现了先减小后增大的趋势，表明选取阻尼器型号时有必要进行计算分析以确保阻尼器参数处于合理范围内。

（3）桥塔桩基础所处的土层或场地特性会对悬索桥两岸塔柱的内力和位移均产生一定影响。

（4）粘滞阻尼器的减震效果由阻尼系数C及速度指数α共同决定，综合考虑减震效果及阻尼器自身特性，建议阻尼器参数C=2 000 kN/（m/s）α，α=0.3。

参考文献

[1]JTG/T 2231-01-2020 公路桥梁抗震设计规范[S].

[2]叶爱君，范立础.附加阻尼器对超大跨度斜拉桥的减震效果[J].同济大学学报：自然科学版，2006（7）：859-863.

[3]鲁传安，胡世德，叶爱君.强震区大跨高墩连续梁桥抗震性能研究[J].结构工程师，2007（6）：56-61.

[4]张永亮，陈兴冲，吴海燕.基于粘滞液体阻尼器的铁路钢桁梁桥减震研究[J].世界地震工程，2009，25（4）：97-102.

[5]张常勇，王志英，王宏博.长联大跨连续钢桁梁桥减隔震设计研究[J].公路交通科技，2015，32（8）：80-88.

[6]李金铭.长联大跨连续钢桁梁抗震型式研究[J].铁道标准设计，2016，60（1）：55-58.

[7]毛玉东，李建中.大跨连续梁桥纵向减震机理和减震效果分析[J].同济大学学报：自然科学版，2016，44（2）：185-191.

[8]杨华平，钱永久，樊启武，等.大跨铁路钢桁连续梁桥减隔震方案比较研究[J].地震工程学报，2017，39（6）：1097-1104.

[定稿日期]2021-05-06

[作者简介]宋松科（1982～），男，硕士，高级工程师，从事桥梁设计与研究工作。