考虑扰动效应的透水管桩地基土固结效果有限元分析
牛 顺,肖 涛,冯健雪,4,阮志环,梅国雄
(1.广西大学 土木建筑工程学院,南宁 530004;2.广西大学 工程防灾与结构安全教育部重点实验室,南宁 530004;3.广西防灾减灾与工程安全重点实验室,南宁 530004;4.贵州民族大学 建筑工程学院,贵阳 550025)
1 研究背景
预制管桩由于具有质量稳定、造价低、振动小及承载力高等显著优点,在软土地区中得到了广泛的应用[1-2]。然而,由于软土通常具有高含水率、低渗透性等特征,预制管桩在沉桩过程中不可避免地会产生挤土效应,从而产生超静孔隙水压力。沉桩结束后,桩周土中的超静孔压逐渐消散,桩土接触边界的有效应力逐渐增加,预制管桩的承载力亦随之增长[3-4]。而缓慢消散的超静孔压直接影响桩的承载力时效性,从而导致施工进度缓慢和对相邻建筑物产生不利影响[5-9]。
针对沉桩产生超静孔隙水压力造成的不良影响,目前工程中,常采用的应对措施有:防渗防挤壁[5]、合理安排沉桩顺序[10]、先开挖基坑后沉桩[11]等方法,以减小挤土效应带来的影响。然而,上述方法均属于施加额外的施工条件和施工步骤来控制超静孔隙水压力,从而影响工程效率。透水管桩[12-13]技术通过在自身桩体开设排水通道,不仅可以很好地解决沉桩产生超静孔隙水压力这一问题,且无需添加额外的施工步骤。目前已有大量研究证明了透水管桩技术的可行性:数值模拟方面,周小鹏等[14-15]利用ABAQUS有限元模拟了透水管桩沉桩的过程,验证了透水管桩在固结效率方面优于普通桩;Dai等[16]对不同开孔大小及开孔数量下的PC管桩进行了承载性能的数值模拟,得到了相应工况下透水管桩的应力-应变规律。试验验证方面,黄勇等[17-18]通过室内模型试验,探究了透水管桩桩周土超静孔压随时间、空间的变化规律,并通过改变初始排水时刻,得出了透水管桩沉桩完成即刻排水会降低土体整体超静孔压水平的结论;Ni等[19-20]通过进行透水管桩单桩以及群桩模型试验,进一步验证了透水管桩加速超静孔压消散的特性,并通过透水管桩抗压、抗弯等力学试验,得出了保证桩身整体强度时的最优开孔率;雷金波等[21-22]对3种开孔方式的带帽有孔管桩复合地基进行模型试验,结果表明有孔管桩复合地基桩周土的承载力高于无孔管桩复合地基。然而,上述对透水管桩的研究中并未提及扰动效应对透水管桩桩周土固结产生的影响。
在桩的打设过程中,会对桩周土体产生扰动进而形成扰动区,在此扰动范围内土体的径向渗透性会降低,超静孔压的消散又与土体渗透性密切相关,进而影响桩的承载力时效。因此,扰动效应对桩周土超静孔压的影响范围及影响程度这一问题就显得尤为重要。目前关于沉桩产生扰动效应的研究主要是针对不透水桩,而对透水管桩扰动效应的相关研究甚少。
本文利用有限元分析软件对透水管桩沉桩后的桩周土固结进行建模计算,然后对模型进行退化验证,并与模型试验中的实测超静孔压径向变化进行对比验证;探究考虑扰动效应时透水管桩沉桩后桩周土的固结特性,并进一步探讨扰动效应下不同开孔率η、开孔半径r0、单层开孔数n等几何参数下桩周土超静孔压随时间、空间的分布规律。
2 计算模型及有限元建模
2.1 计算模型
2.1.1 模型的建立
图1为透水管桩地基土计算模型。其中,H为桩的贯入深度,rw为桩半径(外径),kr、kv分别为土体水平和竖向渗透系数。rd、rp、re分别表示扰动区半径、塑性区半径及影响区半径,u0(r,z)表示扰动区范围内产生的初始超静孔压。

图1 透水管桩地基土模型示意图Fig.1 Schematic diagram of soil foundation model of permeable pipe pile
2.1.2 固结控制方程
沉桩结束后,桩周土中的超静孔压会沿着径向和竖向消散,参考Randolph等[23]关于饱和软土沉桩问题的研究,桩周土体固结控制方程为
(1)
式中:u为土体中产生的超静孔压(Pa);mv为土体体积压缩系数(Pa-1);z为土体任一点距离土体表面的深度(m);r为土体径向任一点到桩中心点的距离(m);γw为水的重度(kN/m3);t为时间(s)。
2.1.3 初始条件
沉桩过程主要是桩身与桩侧土体发生置换,桩底部土体的应力变化类似球体膨胀问题,而沿着桩身竖向呈现圆柱形膨胀[2,23-25]。本文假定沉桩产生的初始孔压分布范围为扰动区,且沿水平方向对数衰减,沿深度方向线性增加,故桩周土体固结的初始条件为
式中p0为土体不排水剪切强度cu的相关参数,根据资料[1],p0取为4 000 Pa/m。
2.1.4 边界条件

2.2 有限元建模
结合前文的固结方程、初始条件以及边界条件,本文采用COMSOL多物理场数值模拟软件进行建模计算,图2为透水管桩地基土有限元计算模型。根据相关研究中常见的桩长径比大小[14-15],取桩的贯入深度H=10 m,桩半径(外径)rw=0.25 m。相关研究表明[26-29],挤土贯入桩超静孔压分布范围一般约为20倍桩径或5~10倍塑性区半径,故本文取影响区半径re=20rw=5 m,塑性区半径rp=1/5re=1 m。根据南宁市周边软黏土相关性质参数,地基土的模型参数如表1所示。透水管桩开孔几何参数见表2,其中土体径向与竖向的渗透、固结系数均相等。

表1 地基土模型参数Table 1 Parameters of soil foundation model

表2 透水管桩开孔几何参数Table 2 Geometric parameters of opening of permeable pipe pile
如图2所示,计算采用自由四面体网格单元对土体及桩进行分析,并设置相应的时间步以研究不同时刻桩周土的固结变化。图3为透水管桩开孔方式示意图。

图2 有限元计算模型及网格划分Fig.2 Finite element model and mesh division

图3 透水桩开孔方式示意图Fig.3 Schematic diagram of opening patterns on permeable pipe pile
3 模型退化及对比验证
3.1 模型退化
本文通过透水区域区分透水管桩和普通桩,为研究方便,定义透水管桩桩身开孔率η为
(3)
式中:r0为透水孔半径;n为单层透水孔数量;m为开孔层数;H为桩长。结合上式,为便于分析,下文采用η=0表示普通桩。
3.2 理论解对比验证
为验证前文数值建模的准确性,将透水管桩模型的退化为开孔率η=0的普通桩,并与高子坤等[30]的研究结果进行对比。本文参考文献[30]的桩土相关参数,利用数值分析软件计算退化后桩周土体的固结度,并给出了与文献[30]解析解的对比结果,如图4所示。由图4可知:透水管桩退化后的数值计算固结度曲线与文献理论解曲线的结果基本一致,较好地验证了数值模拟的准确性。

图4 退化数值解与文献[30]解析解的对比Fig.4 Comparison between calculation of this paper and the solutions of Gao Zikun[30]
3.3 试验对比验证
将本文的模拟结果与Ni等[19]的透水管桩加速超静孔压消散的单桩模型试验研究结果进行对比,以进一步验证透水桩建模计算结果的准确性。图5为该试验的单桩模型示意图,桩长900 mm,桩直径D为60 mm。桩身透水孔直径为6 mm,每层开孔数量为4个,对称分布,层间距为36 mm。桩周土体中共埋设9个孔隙水压力传感器,在竖向分3个高度埋设,分别距离土体表面200、450、700 mm;在水平方向,分别距离桩侧60 mm(1D)、180 mm(3D)、300 mm(5D)。

图5 透水桩模型试验单桩示意图Fig.5 Sketch of model-scale laboratory test for single permeable pile
本文参考文献[19]中土体物理参数及透水管桩几何参数取值,通过有限元模拟计算,得到透水管桩沉桩结束时桩周土超静孔压的计算云图,如图6所示。并模拟出了沉桩后时间分别为t=1、5、10 h时不同深度处超静孔压沿径向的变化,将计算值与实测值进行对比,如图7所示。由图可知,本文通过数值模拟得到的超静孔压消散变化规律与实测结果基本一致,进一步验证了数值模拟的准确性。

图6 超静孔压计算云图Fig.6 Contours of calculated excess pore water pressure

图7 不同深度处超静孔压实测值[18]与计算值对比Fig.7 Comparison of excess pore water pressure at different depths between measurement[18] and calculation
4 扰动效应及桩周土固结分析
4.1 扰动效应影响因素分析
类似于砂井地基固结问题,相对于未扰动土,扰动区内土体主要是在水平方向的渗透系数有所降低[31],而透水管桩是通过在桩身设置径向排水路径,对径向的孔压消散起到了很好的加速作用,因此,本文主要考虑扰动效应对土体水平渗透系数产生的影响,而忽略其对土体竖向渗透系数的影响。
对于普通不透水管桩对土体产生的扰动规律已有许多研究,且对沉桩产生超静孔压大小及其分布规律进行了详细分析。根据Bozouk等[26]、Hwang等[29]及贾志刚等[8]对沉桩后桩周土体孔压变化的监测结果分析可知,土体受到扰动后的扰动范围通常大于或等于塑性区半径,即rd≥rp,故将表示扰动区范围s取为4、6、8。参考等应变砂井地基固结理论[32],扰动程度系数α取为5、10、15。其中:s=rd/rw,α=kr/ks。kr、ks分别为未扰动土和扰动土的水平渗透系数,α越大表明沉桩对地基土的扰动程度越大。为研究方便,下文中用α=1表示未考虑扰动效应。
4.1.1s对桩侧孔压的影响
桩周土体受到扰动导致桩周土体径向渗透系数降低,桩周土超静孔压的消散速度随之变慢,而超静孔压的消散情况直接影响桩基承载力时效性发挥,故下文主要研究桩周土体超静孔压的变化情况。
如图8所示,给出了不同s情况下,桩侧土体的平均孔压随时间的变化曲线。从图8中可知,当开孔率η、单层开孔数n保持一定时,考虑扰动效应比不考虑扰动效应(α=1)的孔压消散速度明显要慢。尤其孔压消散前期,扰动效应造成的孔压消散差距约为10 kPa,而随着孔压消散的进行这一差距逐渐减小,说明α的变化仅对孔压消散前期的影响显著。此外,还可以看出,当α不变时,桩侧平均孔压随着s的变化并不明显。

图8 s对桩侧平均孔压的影响Fig.8 Influence of parameter s on average excess pore water pressure of pile side
4.1.2α对桩侧孔压的影响
为探究不同扰动程度对桩侧孔压的影响,取α分别为5、10、15,并给出如图9所示不同α情况下桩侧平均孔压的变化曲线。由图可知,当s保持不变时,随着α的增大,桩侧平均孔压曲线也随之上升,说明扰动程度的增大使得孔压消散的速度逐渐下降。此外,随着α的增大,桩侧孔压增加的幅度有所减少,说明α的增大对于桩侧孔压的增长幅度是有限的,桩侧孔压的变化还受其他因素的影响。

图9 α对桩侧平均孔压的影响Fig.9 Influence of parameter α on average excess pore water pressure of pile side
综上所述,扰动范围的增大对于孔压消散速度影响并不显著,相对于扰动范围s,桩侧孔压的消散速度对于扰动程度α的变化更为敏感。
4.2 扰动效应下固结特性分析
由于考虑扰动效应与未考虑扰动效应时桩侧孔压差异较大,而孔压的消散不仅与桩周土的性质密切相关,与桩的几何形状也有一定关联。因此,结合透水管桩的开孔几何参数与扰动效应,进一步讨论桩周土的超静孔压的分布情况。
国企海外形象塑造与中国的国家形象塑造密切相关,涉及到政治、外交、经济、军事等各方面,对企业来说,还涉及到与东道国的政府关系、合作模式、与NGO(非政府组织)及社区打交道的方式、与公众传播媒体的关系,以及如何利用互联网和出版物、如何参与国际会议、如何做好社会责任及公益事业等,是一个较为庞大的系统工程。中国国企要想在“一带一路”征程中继续领跑,对海外形象的塑造必须成为国企海外发展的重要环节,并需要在以下几个方面持续发力:
4.2.1 超静孔压随时间的变化
桩周土体受到扰动后,桩周土体径向渗透系数降低,而透水管桩是在桩侧即径向初始超静孔压最大处设置透水孔,以达到改善管桩透水性能、加速超静孔隙水压力消散的目的。
图10给出了不同开孔方式时,考虑扰动效应的桩周土体竖向平均孔压在不同径向位置上随时间的变化。从图10可以看出,随着径向距离的减小,竖向孔压明显增大,其中,在r=1D(D为桩直径)处,竖向平均孔压为最大,随着时间的推移,竖向孔压整体呈逐渐减小的趋势。对于两种不同开孔方式,竖向孔压的变化仅在r=1D处较为明显,具体体现为在孔压消散初期,交叉开孔的孔压曲线位于均布开孔的孔压曲线之上,而在r=3D及r=5D处,两种开孔方式的孔压变化几乎一致,这说明开孔方式对于土体中整体孔压的影响并不明显。值得注意的是,在r=5D处的竖向孔压呈现先逐渐增大后减小的趋势,这是因为孔压具有滞后传递的特性,随着土体径向距离的增大,孔压传递到相应位置后再随时间逐渐消散。
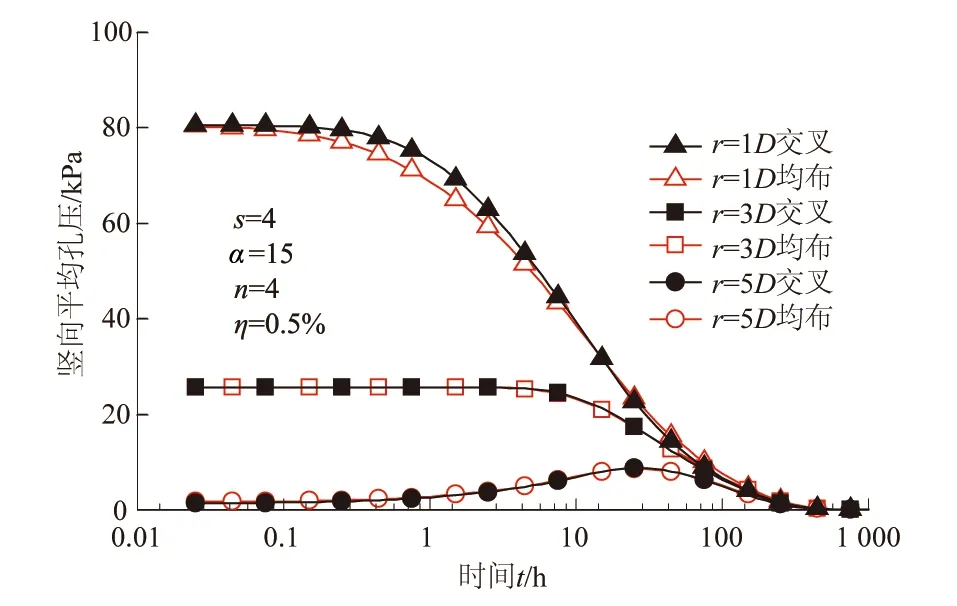
图10 不同开孔方式下竖向平均孔压随时间的变化Fig.10 Dissipation of vertical average excess pore water pressure under different patterns of opening
上述研究表明,不同开孔方式对于桩周土超静孔压的影响并不明显,因此,研究透水桩桩周孔压消散情况时,对于不同开孔方式造成的影响可以忽略。然而,已有研究表明[20],交叉开孔方式对于透水桩的结构性会造成影响(如抗压、抗弯),同时也会对桩的预制工艺带来困难,故下文均采用均布的开孔方式。
参考Ni等[20]进行的透水管桩力学性能试验,当桩身开孔率控制在0.5%以下时透水桩强度的仍有普通桩的80%以上,故本文分别取桩身开孔率为0.1%、0.3%、0.5%。
图11为桩身设置不同开孔率η时,桩侧平均孔压随时间的变化情况,研究表明:随着η的增大,孔压曲线逐渐向下移动,到达相同孔压时所需要的时间逐渐减少,孔压的消散速度随之提高,这是由于随着开孔率的增大,桩身水平方向排水路径随之增多,加速了桩侧的孔压消散。同时,由图11还可以看出,在不同开孔率下,考虑扰动效应的孔压曲线均位于未考虑扰动效应曲线之上,两者之间的差异较为明显。

图11 不同开孔率时桩侧平均孔压随时间的变化Fig.11 Dissipation of average excess pore water pressure on pile side under different ratios of opening
对于桩身均布开孔,由式(3)可知:当开孔率η、孔径r0保持不变时,单层开孔数n与开孔层数m呈反比。图12分别为n=2、4、6时桩侧平均孔压的变化曲线。从图12可以看出:当开孔率η及孔径r0不变时,随着单层开孔数的增加,桩侧孔压逐渐增大,具体表现为孔压曲线上移。这说明随着桩身单层开孔数的减少,即桩身开孔层数的增加,使得桩身竖向的开孔层之间变得密集,此时桩侧孔压的消散速度随之提高。此外,与不同开孔率η时桩侧平均孔压变化类似,不同单层开孔个数n时,考虑扰动效应的孔压曲线均位于未考虑扰动效应曲线之上,两者之间的差异同样较为明显。
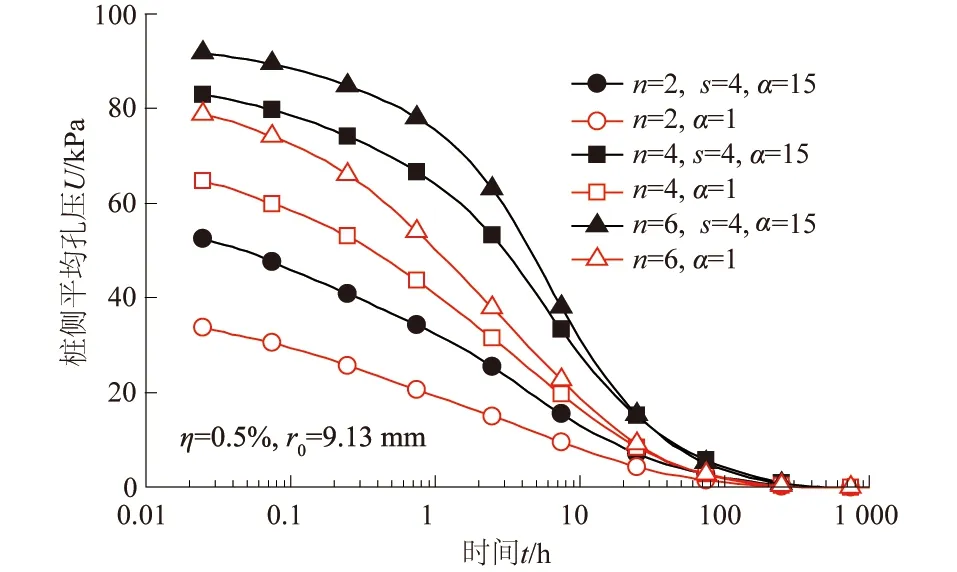
图12 不同单层开孔数n时桩侧平均孔压随时间的变化Fig.12 Dissipation of average excess pore water pressure on pile side under different numbers of drainage holes in a single layer
图13为不同孔径r0对桩侧孔压的影响,r0分别为4.08、7.07、9.13 mm(r0/rw=1.6%、2.8%、3.6%)。可以看出,当开孔率η及单层开孔数n不变时,孔径较小的桩侧孔压小于孔径较大时的桩侧孔压,说明细而密的透水孔使得孔压的消散更快。从图13还可以看出,扰动效应的存在使得桩侧孔压也会发生变化,表现为桩侧孔压明显增大。

图13 不同孔径r0时桩侧平均孔压随时间的变化Fig.13 Dissipation of average excess pore water pressure on pile side under different radius r0 of drainage hole
4.2.2 超静孔压随空间的变化
综合上述结论,将透水桩设置为桩身均布开孔,开孔率η=0.5%,单层开孔数量n=4,开孔孔径r0=9.13 mm的桩型,以探究考虑扰动效应时桩周土超静孔压随空间的变化规律。
如图14(a)所示,为考虑扰动效应时,沉桩结束时在土体深度分别为z=1、5、10 m处的超静孔压沿径向距离r的变化。由图14(a)可知,超静孔压主要分布在距离桩中心2.5 m的范围内,在此区域内的超静孔压随径向距离的增大消散速度较快;同一深度处,超静孔压在距离桩中心越近的位置,其值越大;在靠近桩侧的相同径向距离处,超静孔压最大值随深度的加深而急剧增大,图中z=10 m最大超静孔压达到160 kPa,远大于z=1 m位置处。
如图14(b)所示,为考虑扰动效应下沉桩结束后t=200 h时,超静孔压在不同径向位置r=1.5D、2D、3D处随深度z的变化情况。图中超静孔压大小沿着径向衰减,越靠近桩身,超静孔压越大;图中可见z=10 m 处超静孔压位于峰值状态,从整体上看,随深度增加超静孔压呈线性增大的趋势,最后趋于一定值,这是由于模拟计算的边界条件是土体底部不排水,桩端以下的土体中的超静孔压无法消散导致。
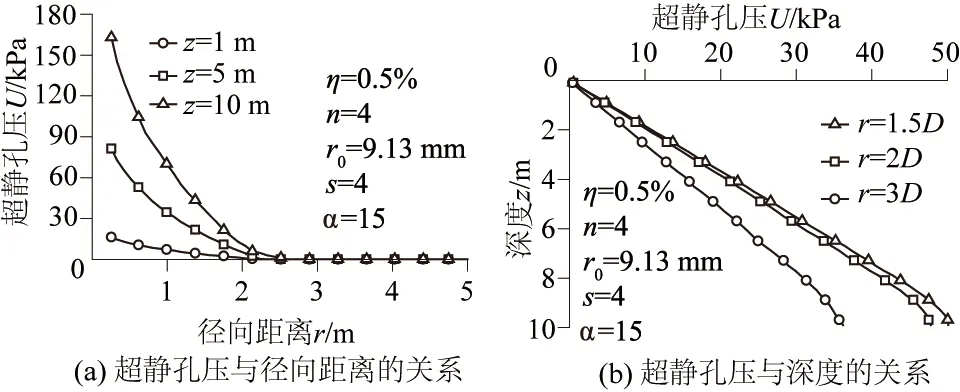
图14 超静孔压与径向距离及深度的关系Fig.14 Relation of excess pore water pressure against radial distance and depth
5 结 论
本文利用有限元分析软件建立了透水管桩地基土三维计算模型,探究了考虑扰动效应时地基土固结变化,并结合透水桩开孔几何参数进一步探讨了扰动效应下透水桩桩周土固结变化,得出以下结论:
(1)透水管桩退化后的数值计算固结度曲线与文献理论解曲线基本一致,较好地验证了数值模拟的准确性。
(2)通过数值模拟得到的超静孔隙水压力变化规律与实测结果基本一致,进一步验证了数值模拟的准确性。
(3)扰动程度系数α的变化仅对孔压消散前期的影响显著,并造成一定程度的孔压消散差,而这一差距随着孔压消散的进行逐渐减小。
(4)扰动范围s的增大对于孔压消散速度影响并不明显,相对于扰动范围s,桩侧孔压的消散速度对于扰动程度系数α的变化更为敏感。
(5)不同开孔率η、开孔半径r0、单层开孔数n下桩周土中超静孔压随时间、空间的变化规律均表明了扰动效应对超静孔压消散速度的影响较为明显,这对实际工程中透水管桩地基固结分析具有一定参考价值。

