江湖系统显式与隐式二维水动力模型比较

周 立,吴 琼,姚仕明，胡德超

(1.华中科技大学 水电与数字化工程学院，武汉 430074；2.长江科学院 河流研究所，武汉 430010)

1 研究背景

对大型江湖河网耦合系统进行整体模拟，目前主要采用的数学模型方法(水动力模型)包括一维模型[1-3]、低分辨率二维模型[4-5]和它们的嵌套模型[6-10]。大型江湖系统高维水动力数值模拟的难点源于“计算区域大”和“整体模拟”。一方面，基于低分辨率计算网格的模型难以准确描述河流、湖泊地形与河势，导致计算精度不足；另一方面，高分辨模型计算量巨大。“计算精度与效率矛盾”使得一维模型统治江湖河网耦合系统水动力研究领域已长达近40 a[1-3]。2009年李琳琳[4]进行了荆江-洞庭湖整体二维水动力数值模拟的首次尝试，她采用低分辨率计算网格(2.6万个尺度为0.6～3 km的三角形单元)剖分计算区域，并使用了商业软件MIKE21显式求解器。然而，她对自己所建立的江湖系统二维模型给出了如下评价：低分辨率计算网格二维模型(由于不能准确描述江湖区域广泛存在的滩槽形态与河势(图1))的精度反而低于一维或一二维嵌套模型。Xia等[11]针对平面二维水动力模型，开展了计算网格尺度对计算结果影响的敏感性分析，结果表明：低分辨率计算网格不能准确描述河道形态、地物等，导致洪水预测结果失真。水动力计算中，精度的优先级高于计算效率。当以高分辨率计算网格作为前提时，大型江湖系统高维水动力模型“计算精度与效率”的矛盾即转化为模型的计算效率瓶颈问题。

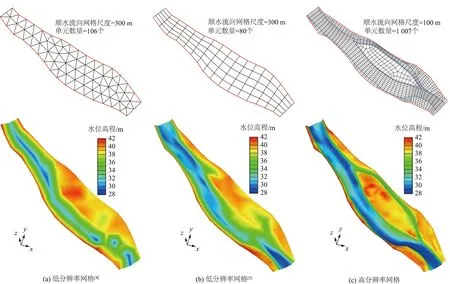
图1 低分辨率计算网格描述河势的失真(以荆南河网某河段为例)Fig.1 Distortion of river regime described by low-resolution computational grid (example of the Jingnan River Network)

根据时间离散方式，水动力模型可分为显式、隐式两大类，它们在稳定性、可并行性等方面差异很大。稳定性直接决定模型可使用的最大时间步长，可并行性直接影响程序对现代多核心计算机等技术的充分利用程度，它们共同决定了水动力模型的计算效率。

显式水动力模型一般是条件稳定的，其计算时间步长受到Courant-Friedrichs-Lewy(CFL)稳定条件的严格限制。传统的欧拉类方法显式水动力模型，在常规计算网格下通常只能使用几秒甚至更小的计算时间步长；优点是具有良好的可并行性。Echeverribar等[12]采用一阶显式有限体积法二维模型和尺度为5～150 m的高分辨率网格(共86.77万个三角形单元)，模拟非恒定流耗时21 d(12核并行)。Xia等[11]基于Godunov型有限体积法二维模型和5～10 m高分辨率网格(约1亿计算单元)，采用GPU并行，模型运行速度约为实际水流运动时间的2.5倍。

隐式模型允许的时间步长可以很大。但是，由于各个单元的计算是耦合在一起的，隐式模型一般是难以并行求解的。区域分解并行是并行化隐式模型的常规方法，例如Sawdey等[13]、Cai等[14]。Cai等[14]使用局部方法并行化求解各子区域所代表的子代数系统，在67.2万计算单元、20核心的算例测试中，并行化模型是串行模型速度的17.1倍。

从稳定性、可并行性的角度讲，显式模型与隐式模型各有优、缺点，显式模型允许的时间步长小但可并行性良好，隐式模型可使用很大的时间步长但并行性较差。在进行大型江湖系统整体平面二维水动力模拟时，显式、隐式模型究竟哪一种更快、更有优势？目前尚不清楚，需进一步研究阐明。本文以荆江-洞庭湖系统为背景，选用MIKE21模型[15]和一种半隐式欧拉-拉格朗日模型[16-17]，开展大型江湖系统整体高分辨显式、隐式水动力模型的计算效率比较研究，来回答这一问题。

2 研究区域

研究区域为荆江-洞庭湖(JDT)系统是一个大型的、强耦合的浅水系统(图2)。整个系统水域面积达3 900 km2，包括荆江、洞庭湖和荆南河网三大子域。洞庭湖位于荆江南岸，同时承纳由荆江松滋、太平、藕池三口分泄入湖的水量和洞庭湖水系湘、资、沅、澧四水的汇入。三口和四水的入流经由洞庭湖调蓄后，在城陵矶处重新汇入长江。JDT系统具有滩槽复式过流断面，导致不同季节江湖区域出现不同流态。例如，洞庭湖在汛期被完全淹没时形成一个湖泊，但在旱季只有类似河流的水流通过狭窄的河道。

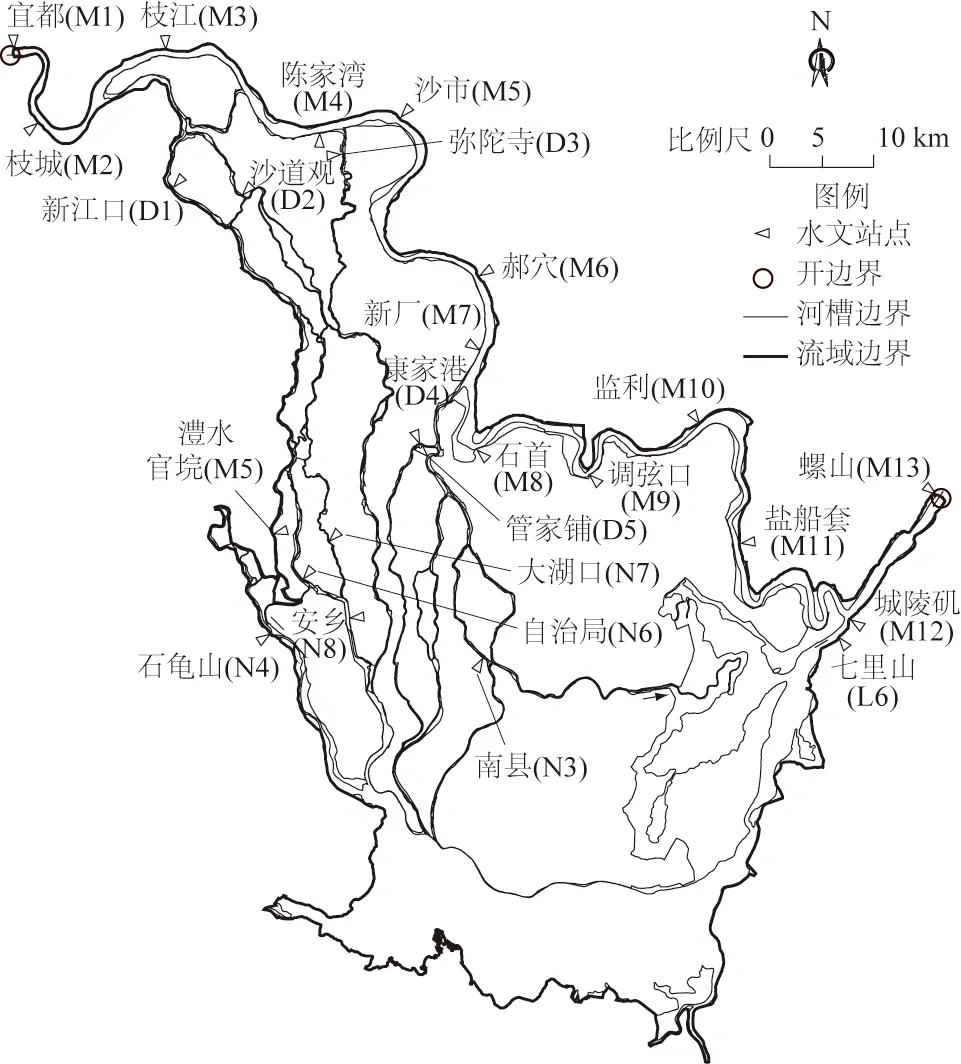
图2 荆江-洞庭湖计算区域Fig.2 Computational domain of Jingjiang-Dongting river-lake system

收集到的JDT系统地形测图分辨率以及测点之间纵向、横向距离，如表1所示。

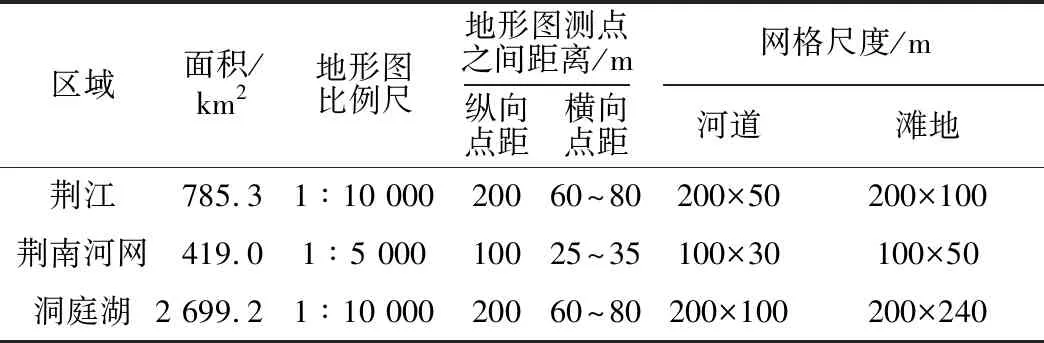
表1 JDT系统地形测图分辨率与计算网格尺度Table 1 Resolution of the bathymetry graph and the com-putational grid scale of Jingjiang-Dongting(JDT)system

根据笔者多年的工程计算经验，当计算网格尺度约等于地形测图测点间距时，所建立的计算网格通常可以较好地描述河道的非规则边界、滩槽形态及河势，图1(c)就是一个例子。此时，水动力模型已可反映各种中尺度的水流结构，获取很高的计算精度。在工程附近，可辅以局部计算网格加密技术，以提高对工程建筑物的刻画，并获得较好地水动力模型应用效果。如果将计算网格尺度减小到地形测图测点间距以下，水动力模型计算精度的增加并不显著。当计算网格尺度大于地形测图测点间距时，此时水动力模型将不再能准确描述河道的非规则边界、滩槽形态及河势，如图1中的(a)、(b)。本研究采用非滩槽优化的非结构网格，在各个分区根据其测图测点间距分区进行剖分的方式布置计算网格，计算网格分辨率与地形分辨率一致(见表1)。使用较精细的结构化网格剖分河流、湖泊和河网中的河槽，以获得较高的分辨率；滩地、江心洲由相对较大的非结构化网格覆盖，以节约计算单元。然后通过综合网格索引，将2种类型的网格统一起来，计算网格共计包含32.8万个四边形单元。使用上述计算网格，可以用较少的单元准确地刻画滩槽地形与河势形态。

3 模型基本原理

显式模型采用目前应用较为广泛的MIKE21 FM水动力模型[15]，隐式模型采用近期发表的半隐式欧拉-拉格朗日模型[16-18]。下面首先介绍这2种模型的基本架构和数值离散方法。

MIKE21 FM采用守恒形式的平面二维浅水方程、非结构网格、Godunov类型的有限体积法和黎曼近似解求解器，守恒性好，具有模拟急流、间断问题的能力[15]。根据界面左右变量的构造方式不同，Godunov类型的黎曼求解器可分为一阶和二阶精度两种。源项数值离散，使用特征分解迎风方法，以满足静水和谐条件。时间离散，MIKE21提供了低阶的Euler方法和高阶的Runge Kuta方法。MIKE21采用Open Multi-Processing(OpenMP)处理并行，适用于共享内存计算机。显式差分格式计算步长受到Courant-Friedrichs-Lewy(CFL)数稳定条件限制，要求CFL<1，导致模型允许时间步长较小。根据MIKE21软件手册[15]，对于笛卡尔坐标系下的浅水方程，CFL数定义为

式中：Δx、Δy分别为x方向和y方向的增量；Δt为时间步长；u、v分别为x方向和y方向的速度；g为重力加速度；h为总水深。

半隐式欧拉-拉格朗日模型[16-18]采用非守恒形式的二维浅水方程，并使用算子分裂法将动量方程拆成若干亚方程进行求解。为消除快速重力波的稳定性限制，采用θ半隐法将水位梯度项分为显式和隐式两部分进行离散求解[16]；采用欧拉-拉格朗日法(ELM)求解对流项；显式中心差分法离散水平扩散项。为保证质量守恒，使用有限体积法离散连续性方程。θ半隐法方法消除了快速表面重力波运动对时间步长的限制，ELM消除了对流作用对时间步长的限制。θ半隐法方法、ELM的联合使用，使得上述隐式模型的计算时间步长不受CFL条件限制，所以模型具有良好的数值稳定性。对于隐式水动力模型而言，源于u-p耦合产生的大型代数方程组的并行求解，一般是较困难的。本文采用文献[16]报道的预测-校正分块并行计算方法，进行隐式水动力模型u-p耦合的并行求解。与MIKE21相对应，仍然采用OpenMP技术实现隐式模型在共享内存的多核计算机上的并行计算。

4 水动力模型参数率定

在使用荆江-洞庭湖平面二维水动力模型之前，需要确定计算区域河床糙率nm。一般而言，平滩流量是最具有代表性的水流条件，根据余文畴的研究即荆江枝城水文站平滩流量为30 000 m3/s[19]。本文参照2005年8月1—3日发生在荆江-洞庭湖系统中的实际水流条件，进行平均处理，作为系统的平滩水流条件，用于模型糙率参数率定。在平滩流量水流条件下，采用分块率定的方法确定江湖河网系统曼宁糙率系数nm取值，具体方法见文献[16]及文献[17]。选取半隐式欧拉-拉格朗日模型，开展河床阻力参数率定及模型计算精度的验证，作为后文效率测试的基础。在平滩流量水流条件下，经过水位、流量双重率定计算，最终得到：荆江、荆南河网和洞庭湖的率定值从上游到下游分别为0.026～0.018、0.026～0.020和0.019～0.018。在使用上述糙率进行水流模拟时，计算得到的水文站点的水位值、流量值与实测值符合良好。

以上述率定的nm分布为基础，选取2012年作为典型年，开展数学模型计算精度的验证。计算得到的水文站点流量过程、水位过程与实测资料的比较如图3所示。然后，对2012年JDT系统中的非定常流过程进行了数值模拟，验证了准确性，流量的计算误差一般在5%以内，水位的计算误差一般在0.15 m以内。上述数学模型计算得到的流量、水位年变化过程均与实测资料符合较好，该率定验证结果表明：所使用的平面二维水动力模型能较好模拟JDT系统水流运动，数学模型计算方法是可行的，参系数取值合理，满足工程实践应用的精度要求。

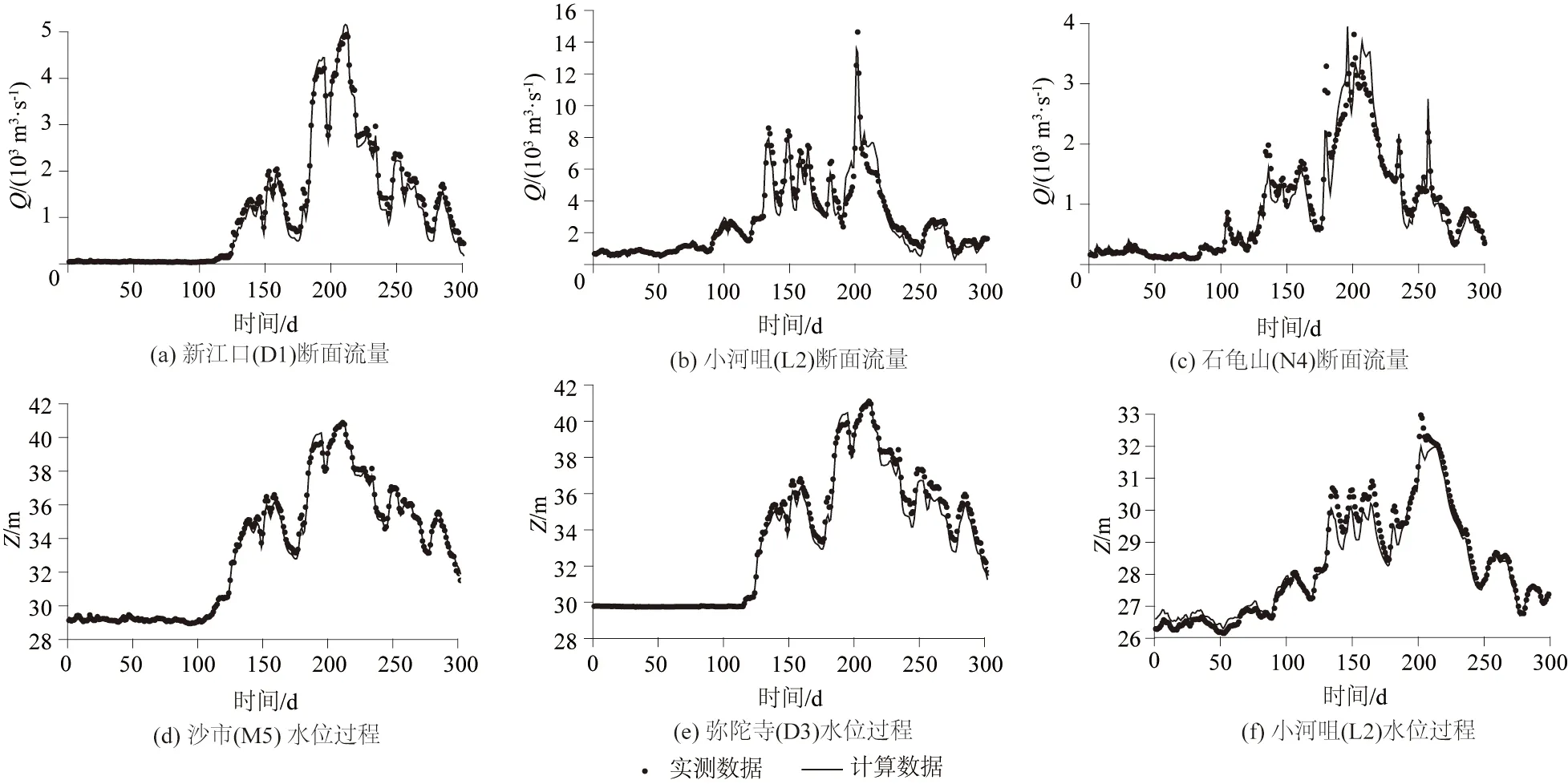
图3 计算的断面流量、水位过程与实测资料的比较Fig.3 Comparison of discharge and water level process between calculation and measurement

5 模型稳定性与计算效率测试

5.1 测试条件

硬件环境为具有16核处理器的共享内存计算机(Intel Xeon E5-2697a v4,clock speed:2.6 GHz)，关闭超线程技术。采用Microsoft Windows 7作为软件运行环境。MIKE21软件使用MIKE ZERO 2014版本。半隐式模型程序运行环境为Microsoft Windows 7 and C++ 14.0。

加速比(Sp)定义为串行运行时间与并行运行时间之比，即

Sp=T1/Tnc。

(2)

式中：T1为使用1个核心运行(串行)一个计算程序所消耗的时间；Tnc为使用nc个核心运行(并行)一个计算程序所消耗的时间。

使用JDT系统对MIKE21与半隐式欧拉-拉格朗日模型进行测试，以阐明显式、隐式模型在模拟大型江湖系统水流运动时稳定性和效率的差异。选取2种典型的水流条件进行测试，分别为恒定流和非恒定流条件。恒定流流动条件选择最具有代表性的平滩流量，非恒定流条件采用JDT系统2012年非恒定流过程。

5.2 数值稳定性测试

在测试中，当时间步长(Δt)达到90 s，仍可保证良好的数值稳定性和取得精确的模拟结果。所选用的显式模型(MIKE21水动力模型)时间步长需严格满足CFL稳定条件。以荆江干流为例，最大水深约50～60 m，最大流速可达4 m/s，最小计算网格尺度取50 m，代入式(2)计算，可知CFL<1稳定条件理论上所允许的最大时间步长为2 s。在模拟天然实际河道时，由于局部河道地形变化剧烈、干湿动边界频繁转换等原因，MIKE21水动力模型允许的最大的Δt下降至0.8 s。

5.3 计算效率测试

其一，在平滩流量水流测试条件下，分别使用nc=1、2、4、8、16，测试隐式和显式数学模型的计算效率。为了保证每种测试条件下，所运行的计算程序占用CPU缓存基本接近，在nc≤8的测试条件下，相应地增加同时运行的程序的数量，以近似平分CPU的缓存。显式模型(MIKE21模型)和隐式模型(半隐式欧拉-拉格朗日模型)完成1 d的水流模拟所需要的时间如表2所示。由表2可知，显式模型在nc=16测试条件下的加速比Sp=15.8，与此同时，隐式模型的加速比Sp=11.1。随着nc数量的增加，显式模型由于各个单元或节点计算的独立性，保持着良好的加速性能；隐式模型由于使用了预测-校正分块并行计算方法，在nc=16时仍保持着很大的加速比。在平滩流量水流测试条件下，显式模型的计算耗时是隐式模型的35.4～50.8倍。

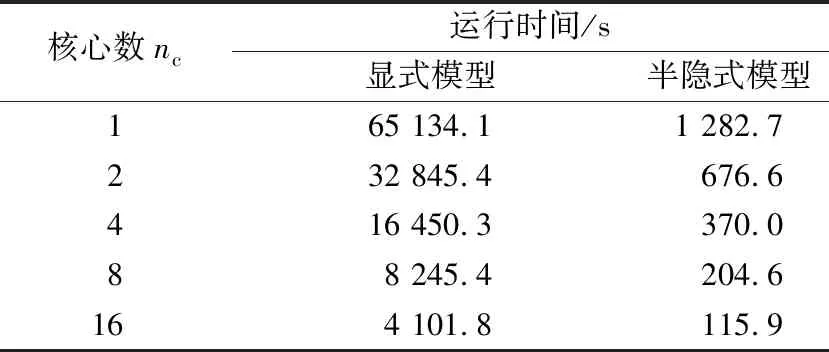
表2 显式、隐式1 d水流模拟所需要的时间Table 2 Time of explicit and implicit models for simulating one-day flow process

其二，在2012年实测水流边界条件下，使用nc=16测试隐式和显式数学模型的计算效率。根据模型运行中的时间记录，显式模型模拟1 a的非恒定流过程需要411 h，半隐式模型需要10.76 h。在非恒定流测试条件下，隐式模型的计算效率是显式模型的38.2倍。

6 讨 论

本文以荆江-洞庭湖系统为背景，建立基于高分辨率计算网格的平面二维显式与隐式水动力模型，开展模型性能的比较研究，探讨将高分辨率高维水动力模型用于模拟大规模浅水系统的可能性。以下将围绕“分辨率与计算精度”“显式与隐式模型特点”“高分辨模型实际意义”3个方面展开讨论。

6.1 高分辨率与低分辨率计算网格的显式模型

低分辨率与高分辨率显式模型，在计算精度、稳定性、计算效率方面的差别如下。

(1)计算精度。一维数学模型由于控制方程简化无法完全反映水流运动物理特性，因而精度不高。李义天[19]曾对国家“九五”期间长江科学院、中国水利水电科学研究院等多家单位的三峡水库下游一维江湖模型计算成果进行比较，发现它们的水位计算误差可达-1.412～1.932 m。低分辨率计算网格(图1中的(a)[4]、(b)[5])不能准确描述平原江湖系统中广泛存在的滩槽分布与复杂河势。根据文献[4]，基于低分辨率计算网格的平面二维水流模型在中小流量条件下的计算精度甚至低于一维模型或一二维嵌套模型。本文采用包含32.78万个四边形的高分辨率网格(图1(c))改善模型计算精度，水位、流量计算误差一般分别在0.15 m、5%以内，较以往的江湖河网数学模型(一维模型、低分辨率二维模型及它们的嵌套模型)[2-4]计算精度提高约1个数量级。

(2)数值稳定性。文献[4]在进行荆江-洞庭湖平面二维水动力模型建模时，采用粗尺度计算网格(2.6万个尺度为0.6～3 km的三角形单元)剖分计算区域。根据CFL条件估算，她使用的MIKE21显式水动力模型的时间步长在理论上不能>12 s，在真实江湖复杂地形、干湿动边界频繁转换等的扰动下，实际能达到的时间步长还需减小数倍。本文采用包含32.78万个四边形的高分辨率网格，最小网格尺度缩小约为50 m。在同样使用MIKE21显式求解器时，测试表明能够保证稳定计算的最大时间步长仅为0.8 s。

(3)计算效率。文献[4]采用仅含有2.6万个三角形的低分辨率网格和MIKE21模型，模拟荆江-洞庭湖1 a水流过程需140 h。若改用高分辨率计算网格，考虑到计算网格数量增加、CFL稳定条件对时间步长的限制，模型耗时将呈数量级的增加。本文采用包含32.78万个四边形的高分辨率网格MIKE21模型进行测试，在16核心并行的计算机条件下，模拟1 a非恒定流过程耗时约411 h，换算为串行运行计算时间约为6 526 h。由此可见，在使用高分辨计算网格代替低分辨计算网格后，计算耗时将增加约47倍。从大型江湖系统整体平面二维水动力模拟的效率来看，显式模型尚难以满足实用速度的要求。

低分辨率模型难以准确模拟河势演变，高分辨模型存在计算效率严重不足、难以实用的瓶颈，正是由于这些不利情况，使得一维数学模型的使用率在江湖河网耦合系统水动力研究领域领先多年[20-22]。

6.2 高分辨率计算网格的显式模型与隐式模型

在相同的高分辨率计算网格与河床糙率取值条件下，荆江-洞庭湖平面二维显式与隐式平面二维水动力模型所取得的计算结果基本一致。下面重点比较两类模型的数值稳定性和计算效率。

(1)计算的时间步长。本文所使用的半隐式欧拉-拉格朗日平面二维水动力模型的时间步长不受快速表面重力波运动、对流作用等的限制，在时间步长为45、60和90 s时，都可保证良好的数值稳定性并取得精确的模拟结果，本文在测试时使用Δt=60 s。与此同时，MIKE21的计算时间步长由于受Courant数稳定条件限制，理论上要求CFL<1,经过实际测试，在JDT高分辨计算网格条件下，其Δt最大只能取至0.8 s。相比之下，隐式水动力模型的时间步长可达到显式模型的75倍以上。

(2)计算效率。显式模型的加速比随核心数量基本呈现线性变化，隐式模型在使用了预测—校正分块并行计算方法时，亦可取得非常大的加速比，加速比随核心数量呈现为亚线性变化。在串行计算条件下，模拟1 d恒定流过程的测试中，显式模型耗时近18.1 h，隐式模型耗时约0.36 h，后者计算效率为前者的50.8倍。在16核并行计算条件下，模拟1 a非恒定流过程，显式模型耗时411 h，隐式模型耗时10.76 h，后者计算效率是前者的38.2倍。

7 结 论

本文以荆江-洞庭湖系统为背景，选用MIKE21模型和一种半隐式欧拉-拉格朗日模型，开展大型江湖系统整体高分辨(32.8万个四边形单元,最小网格尺度约50 m)显式、隐式水动力模型性能的比较研究。结论如下：

(1)模型率定验证结果表明：高分辨率计算网格平面二维水动力模型流量的计算误差一般在5%以内，水位的计算误差一般在0.15 m以内，较以往的江湖河网数学模型(一维模型、低分辨率平面二维模型及它们的嵌套模型)计算精度提高约1个数量级。

(2)在基于高分辨计算网格模拟JDT水流运动时，显式模型稳定性较差，时间步长一般不能超过0.8 s；隐式模型稳定性好，时间步长可达60 s以上。隐式模型时间步长可达到显式模型的75倍以上。

(3)典型水流条件下的模型并行加速性能测试结果表明，显式模型具有良好的可并行性，加速比随核心数量基本呈现为线性变化；隐式模型在使用了预测-校正分块并行计算方法时，亦可取得非常大的加速比，例如，隐式模型在nc=16测试条件下的加速比Sp可达11.1。

(4)在整年非恒定水动力过程的模拟测试中(使用16核心并行计算)，显式、隐式模型的耗时分别为411、10.76 h。从数学模型的绝对计算效率来看，隐式模型的计算效率是显式模型的38.2倍。在基于高分辨率计算网格开展大规模浅水系统整体水动力模拟时，隐式模型计算效率是显式模型的数十倍，可极大地提高大型江湖系统整体高维数学模型的实用价值。