耗散响应理论及其在开放系统中的应用*

陈宇

(中国工程物理研究院研究生院,北京 100193)

近些年来,随着实验技术的进步,对量子多体系统的耗散控制能力得到了增强,同时耗散动力学过程表征技术方面的实验也有了较大进展.实验上的进展驱使我们在理论上建立量子多体系统的耗散动力学计算体系.最近我们发现,通过把系统和环境之间的相互作用看成对系统的一个微扰,可以得到一般性的耗散响应理论.通过这一响应理论,可以回答物理可观测量以及熵在耗散下一定时间尺度内的动力学演化的问题.本文建立了非Markov 环境下的一般理论,并讨论了何时可以取到 Markov 近似,同时综述了这种方法在计算强关联体系的耗散动力学、强相互作用开放体系的熵的动力学演化等方面的应用.

1 引言

线性响应理论是物理学中各种测量的基础[1].线性响应的基本精神是通过探测物理量在一个微小驱动后的含时演化来研究物理体系的性质.在凝聚态物理的实验中,有许多实验是以线性响应作为基础的,如角分辨光电子谱实验(APRES)、电导测量、中子散射等.这些实验都采用外场来耦合系统中的某些物理量,最终测量物理量之间的推迟关联性质.

线性响应的精神主要体现在外场为弱场时,对复杂的非平衡动力学演化行为的研究可以被约化为对初始时刻平衡态系统性质的研究.仔细考察线性响应理论与实验的真实设置之间的差别时可以发现,其中一个重要的近似在于使用的外场是环境中算子的期待值,而外场的涨落所造成的效应被完全归零了.真实的线性响应实验总是一次环境和系统突然耦合的过程,而在有些时候外场涨落引起的效果是无法被忽略的.特别是在外场的期待值为零的情况下,体系的动力学行为是完全被外场涨落驱动的[2].

本文将主要研究这种外场期待值为零时体系的耗散动力学行为.第2节首先给出耗散响应理论的一般性理论.这里的一般性理论主要是指一般的非Markov 环境.耗散响应理论包括对物理可观测量的耗散响应和熵的耗散响应两个方面.同时,给出Markov 极限的条件以及在这个极限下的非厄米线性响应理论[3].第3节介绍非厄米线性响应理论在Bose-Hubbard 模型的耗散动力学中的应用[2].第4节介绍如何把熵的耗散响应理论用于具有全息对偶映射的开放Sachdev-Ye-Kitaev 模型中,从费米子热化的角度来看引力侧黑洞蒸发问题中的Page 曲线[3].最后对耗散响应理论进行总结和展望.

2 耗散响应理论

考虑一个物理体系在某一时刻突然和环境发生耦合.在耦合前,系统和环境的哈密顿量可以写为

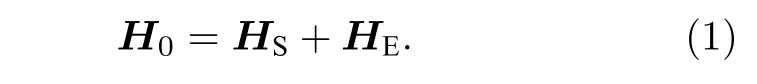
在与环境耦合以后,其总的哈密顿量变为

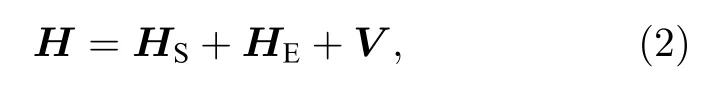
其中

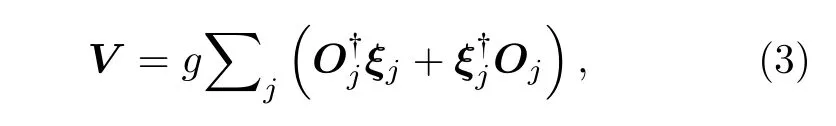
这里Oj是作用在系统的Hilbert 空间上的算子,ξj是作用在环境Hilbert 空间上的算子.j是模式指标,也可以看作类似空间指标的连续指标.总系统的演化服从下面的动力学方程:

其中ρ0和ρE是系统和环境的初始密度矩阵.由于体系的含时演化是一个幺正的过程,因此系统的密度矩阵以及环境的密度矩阵的迹都不随时间变化.这一点是非常重要的,一个密度矩阵的含时演化是保持迹不变的,与幺正性是互相等价的,这是量子力学的基本要求.然而在近来许多有关非厄米演化的研究中,并不能保证一个密度矩阵在演化过程中保持迹不变.因此,这种非厄米哈密顿量的近似在量子开放系统中的有效程度和适用范围是值得进一步清晰化的.因为迹不变,所以可以把TrE(ρE(t))替换为初始热态的配分函数ZE=TrE(ρE).为了简单起见,后文用 Tr取代 TrS来表示对系统的 Hilbert空间求迹.

根据(4)式,得到在相互作用表象下的系统密度矩阵为

这里θ12=θ(t1-t2),是阶梯函数的简写,当t1＞t2时θ12=1,当t1＜t2时θ12=0,t1=t2时θ12=1/2.

微扰公式(10)式可以用一系列图形来表示(如图1和图2).图形规则如下:所有沿径向向内侧走的实线表示在实时上的正方向演化,向外侧走是向时间的反方向演化;其中蓝色的线表示按照环境的哈密顿量进行演化,黑色的实线表示按照系统的哈密顿量进行演化;沿角向走的实线表示虚时间演化(黑色是系统的虚时演化,蓝色是环境的虚时演化),如果闭合表示求迹;虚线表示相互作用强度g;箭头表示演化的方向,算子按照箭头的方向依次作用;红色的点表示在系统中的产生算子O†,红色的叉表示系统的湮灭算子O;相应地,蓝色的点表示在环境中的产生算子ξ†,蓝色的叉表示在环境中的湮灭算子ξ;黑色算子在右侧多一个 —i因子,在左侧多一个i 因子.

图1 耗散费曼图图形规则演示图Fig.1.Illustrations of the diagram rules of the dissipative Feynman diagrams.

相互作用表象下的密度矩阵微扰结果可以用上述图形方法画出,如图2所示.

图2 (10)式的图形表达.这一图形法则可以用于高阶图的展开Fig.2.Diagram expressions of Eq.(10).

2.1 物理可观测量的线性响应理论

下面考虑一个系统的物理可观测量W,那么在零时刻系统与环境突然接触以后,物理可观测量随时间的动力学变化是后者正好可以用前面引入的图形规则表示.

在展示结果之前,让我们回到更为熟知的线性响应理论的出发点.假设

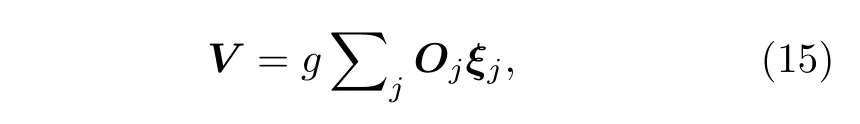
这里的Oj和ξj都是厄米算子,即更为一般地不假设〈ξj〉=0.

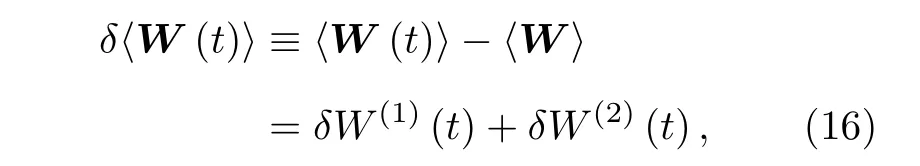
其中δW(1)(t)和δW(2)(t) 是按照g的阶数来定义的.显式的定义如下:

当外场的平均值非零,且被测量的物理量正好是O时,有

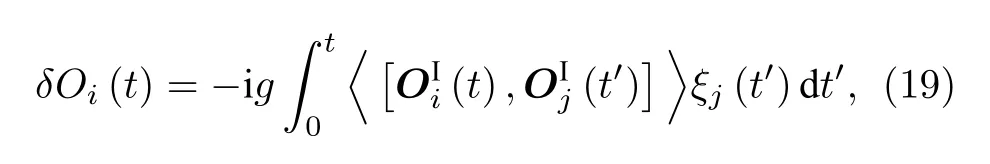
其中重复的j指标代表求和,这正是我们所熟知的线性响应理论.同时根据推导就不难发现,在更高阶的贡献中,既包括关于外场的非线性响应的部分,也包括由于外场的涨落引起的响应部分.接下来将证明在考虑外场均值为0 时,涨落引起的耗散响应在马尔可夫极限下正好是之前发现的非厄米线性响应理论.

我们也发现,一般而言,除了在一些极限情况下,增益都会有自己的记忆效应.只有耗散是可以完全没有记忆效应的.也可以注意到,量子噪声的条件和经典噪声的条件对于环境来说差别是非常大的.同时也看到,在马尔可夫极限下存在增益本身已经把量子系统放在了高温环境中,相干性消失,可以将系统看成一个经典系统来处理.需要注意的是我们现在的处理方法与最早的Feynman-Vernon 影响泛函[4],以及在Caldeira-Leggett 理论中使用的Schwinger-Keldysh 方法[5]略有不同,走了不同的路线.我们所建立的理论的优点在于比较容易计算短时间弱耗散、强相互作用的系统.而仅仅这一优点已经可以回答大量从前在开放系统动力学中难以回答的问题.

2.2 熵的线性响应理论

下面计算系统的熵在突然与环境耦合以后发生的变化.为了简单起见,首先来计算第二 Renyi熵的变化.根据第二Renyi 熵的定义:

以上是玻色子环境与玻色子耦合的情况.

图3 第二Renyi 熵的指数的耗散费曼图Fig.3.Dissipative diagrams of the exponential of the second Renyi entropy.

如果ξ和O是费米场,那么相应地,Renyi 熵响应公式需要修改为

其中的统计核函数为

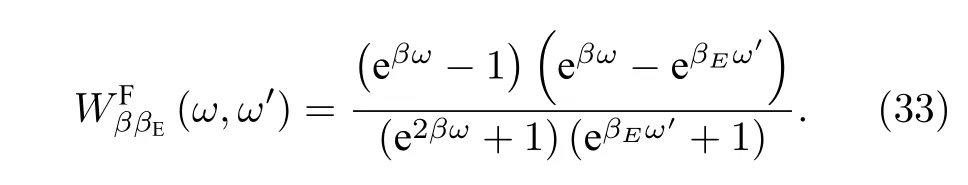
由此得到了熵响应的一般表达式.可以发现在这个表达式中熵的变化仅仅和系统、环境的谱函数、初态温度、以及统计性质有关.(32)式和(33)式也大大简化了对熵的动力学演化的计算[3].

3 耗散Bose-Hubbard 模型中的动力学

近些年来,随着冷原子调控技术的突破,陆续出现了一些有关控制冷原子体系中的耗散的实验研究[6-12].

2019 年巴黎高等师范学院的实验工作中,他们在二维的Bose-Bubbard 模型中引入了耗散[6].实验中他们测量了在0 动量上的粒子占据随时间的改变,以及动量分布的峰宽随时间的变化.他们发现0 动量上的粒子占据数并不是按照指数规律衰减的,同时他们发现动量的峰宽变化比典型的扩散行为要慢一些.过去,在一些近似下,有一些针对Bose-Hubbard 模型的耗散动力学的计算[13,14].

根据 Wick 定理,同时忽略掉高阶的连通图,

下面考虑两种特别的情况.

1)系统有良好定义的准粒子:

容易发现,这样的谱函数会使得f(k,t)=1,故而F(k,t)=t.由此可以发现:

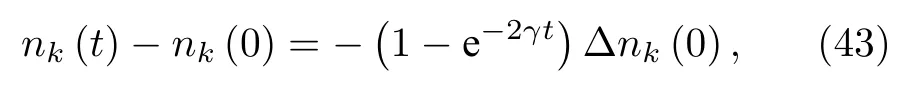
也就是说粒子数的变化是指数衰减的.

2)系统在量子临界点附近.系统没有良好定义的准粒子[15],其谱函数有如下特征:

由此可以计算得到f(k,t)=t2η-2,F(k,t)=t2η-1.这里需要说明的是尽管谱函数和动量有关,但是f(k,t)与动量无关.这时,

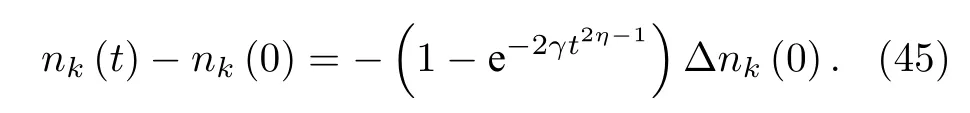
与此同时,

注意后面动量扩散的规律和0 动量粒子数衰变的规律完全相同.而这一结果并不仅仅是粒子数守恒造成的,而是严重依赖于f(k,t) 与动量无关这一事实.因此,这一规律如果在实验上被观测到并非是一个寻常的现象.下面展示一下由本文给出的公式拟合实验原始数据的结果,如图4(a)所示.可以发现动量扩散的数据和粒子数衰变的数据在一定的放缩后完全重合.

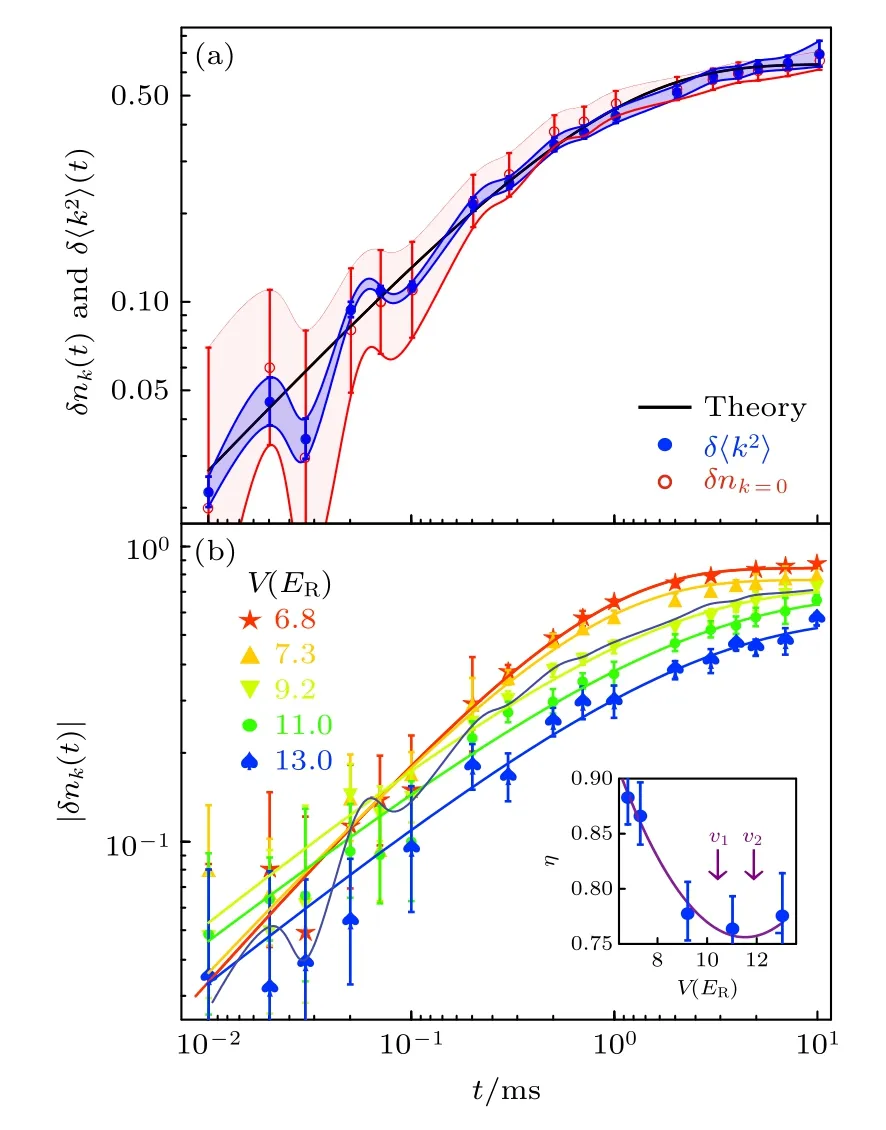
图4 (a)红色为0 动量粒子数衰变的数据,蓝色为动量空间中的粒子数宽度随时间变化的曲线;(b)拟合的不同晶格强度下的Bose-Hubbard 模型中的0 动量粒子数衰变曲线中的参数 .这里的反常维度应该在量子临界点处最小.图(b)的小图里两个箭头所在的晶格强度就是量子临界点所在的位置[2]Fig.4.(a) Red curve shows the decay of zero momentum particle occupation.The blue curve shows how the width of particle momentum distribution evolutes over time.The solid line is our theoretical prediction.(b) Theoretical curve with experimental data for zero momentum particle decay for different parameters.In the inset figure,we shows the anomalous dimension eta extracted from experimental data and we can see its minimal being around quantum critical region[2].

4 非马尔科夫环境中的熵变与Page曲线

第2节中得到了一个系统和环境在突然耦合后熵的变化公式.这里用这个公式以及猜测的引力全息对偶来探讨一下黑洞的信息丢失佯谬.首先回顾黑洞信息丢失佯谬.文献[16-23]中的研究发现,黑洞的表面积和总质量、总角动量满足如下简单的关系:

其中GN是牛顿万有引力常数,Area 是黑洞的表面积,M是黑洞的质量,J是黑洞的角动量,Ω是黑洞视界的角速度,κ是视界表面的引力.后来有人发现这一表达式和热力学基本方程十分相似.其中κ正比于温度,M相当于内能,Area 正比于熵,J相当于体积,Ω相当于压强.因此提出视界的表面积正比于黑洞的熵.

之后霍金考虑在黑洞视界的表面由于量子涨落的原因形成一对纠缠光子对,其中一个光子在视界之内而另一个在视界的外面.其中视界内部的光子掉落向黑洞的奇点,而黑洞外部的光子向无穷远逃逸.在无穷远的观测者于是看到了被辐射出的光子.这些光子被称为霍金辐射.霍金在计算霍金辐射的熵时发现辐射光子的熵随着时间单调上升.但另一方面,随着黑洞因为辐射光子而蒸发,质量减小以后,表面积缩小.因此一定会出现黑洞的熵比辐射出的光子的熵更小的情况.然而,如果假定黑洞的所有动力学过程(包括塌缩和蒸发)都是一个幺正过程的话,体系的细致熵(及部分的冯诺依曼熵)一定满足黑洞细致熵等于霍金辐射的细致熵.另一方面,细致熵一定小于粗粒化的熵(粗粒化熵是指从某些物理可观测量来看,某些等效的分布如正则分布,也可以得到相同的结果时,这些等效密度矩阵的冯诺依曼熵.一般而言在经典的热力学中,热力学分布都取到了系统和环境最大程度退相干的混合态,因此经典熵是粗粒化熵的代表.自然地,我们之前类比黑洞熵和经典热力学熵即是说黑洞的粗粒化熵).这是因为粗粒化过程本身意味着信息的丢失,因此人为造成熵增加.然而根据刚才的论述可以看出,黑洞视界面积的收缩导致的粗粒化熵减小也限制了黑洞的细致熵的大小.而当霍金辐射的熵大于黑洞粗粒化熵时自然就无法继续满足黑洞细致熵等于霍金辐射熵这一条件.这就导致一个问题,黑洞蒸发的过程中是否存在信息丢失?这就是霍金提出的黑洞蒸发的信息丢失佯谬[24].

20 世纪90 年代,霍金的学生 Page[25]提出为了解决这一信息丢失佯谬,霍金辐射的熵会在某个时刻开始减小.这条非单调变化的霍金辐射熵变曲线因此得名.在后来的研究中,有一系列弦理论的计算中支持Page 曲线,暗示黑洞蒸发的过程确实是一个幺正的过程[26-30].1999 年Maldacena[30]发现SU(N)的超对称Yang-Mills 场和引力理论之间存在对偶关系.这里所谓的对偶猜想是指在两个不同的理论下通过某种映射联系起来的场有等价关系,表现为配分函数相同,即所有关联函数都相同.这种对偶映射虽然没有得到严格证明,但在不少理论中得到了一定程度的验证.自然地,如果一个引力理论可以对偶为一个量子力学体系,其动力学演化的过程一定是幺正的,故而满足最初的基本假设.于是不少研究者试图从具有全息对偶性质的引力理论出发,试图从引力侧和量子力学侧同时对Page 曲线进行研究和理解.在全息对偶理论提出以后,很长时间内并没有一个有明确哈密顿量的体系可验证具有全息对偶性质,直到2015 年Kitaev[31,32]、Ye和Sachdev[33]提出 Sachdev-Ye-Kitaev(SYK) 模型,SYK 模型是一个具有哈密顿量的全息对偶模型[34-36].SYK模型被证明和1+1 维的 Jackiw-Teitelboim (JT) 引力[37,38]存在对偶关系[39].由于在大N 极限下,类似SYK 模型是可解的,因此最近有不少工作对这些类SYK 模型的熵变进行了计算[40-48].在引力侧,通过推广的Ryu-Takanagi 公式,最近不少研究也在 Page曲线问题上取得了关键性的进展[49-51].

这里我们试图在一个有全息对偶的SYK 模型上外加一个量子场作为环境,来计算系统的熵的变化.通过前面通过微扰理论给出的公式可以非常一般地计算出环境比系统温度高或者低(环境温度低对应于黑洞蒸发的过程)的熵变.首先写出体系的哈密顿量:

其中j,k,l,m可以取从 1 到 N 的整数,是Majorana费米子的模式数,χj是Majorana 费米子.Jjklm满足:

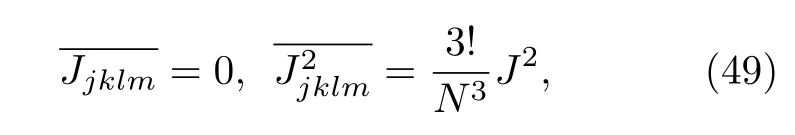
其中上横线表示无序平均,J是一个实数参数,表示费米子之间的耦合强度.这里为了满足大 N 极限以及强耦合极限,需要要求N ≫βJ ≫1.接下来假设环境是无序的自由费米子,

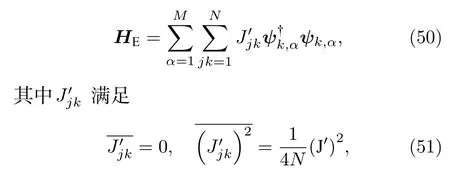
其中上横线表示无序平均,J′是一个实数参数.ψk,α是复费米场.系统和环境之间的相互作用为

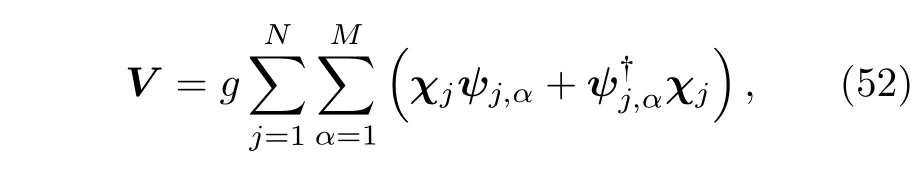
其中g是耦合常数.在上面的假设下,发现有关的谱函数可以给出,为

因此,根据之前建立的熵变的一般公式得到:

由此发现,在短时间的极限下:

注意这个因子是可正可负的.在较长时间里,线性的规律比较接近热传导.接下来展示环境温度较高和环境温度较低时,进入SYK 模型非微扰区的现象.

首先在图5中考虑环境初始温度比较高的情况.可以发现在初始时刻的平方增长以后变为线性增长.

图5 当环境比SYK 系统温度高时系统的熵随时间的变化 (a)环境和系统的谱函数;(b)系统的熵随时间的演化,可以看到经过初期的平方增长后变为线性增大.系统的温度 β=10,相互作用强度 J=4;环境温度 βE=2,相互作用强度 J′=8.该图引用自文献[3]Fig.5.(a)Spectral functions of the environment and the system;(b) entropy dynamics after the quench interaction between the system and the environment.Here the temperature of the environment is higher than the system’s initial temperature.The entropy dynamics shows a typical thermalization case.Cited from Ref.[3].

接下来考虑环境温度比较低的情况,这正好对应于类似黑洞蒸发的过程(如图6所示).从图6可以看出,由于最终的λ ＜0,而初始时刻的熵是平方增加的,因此一定存在一个熵变反转的时刻.由于直接计算的是SYK 模型的细致熵,也就是说对应于黑洞的细致熵.其变化应和霍金辐射的熵相同,因此我们也预期熵的变化服从Page 曲线.这正是我们的微扰理论给出的结果.

图6 (a)系统的谱和环境的谱;(b)“黑洞蒸发”的熵的变化图.系统的温度 β=2,相互作用强度 J=2;环境的温度 βE=20,相互作用强度 J′=2.该图引自文献[3]Fig.6.(a) Spectral functions of the environment and the system;(b) entropy dynamics after the quench interaction between the system and the environment.Here the temperature of the environment is lower than the system’s initial temperature.The entropy dynamics shows a typical cooling case.Here it can be compared with“Black Hole Evaporation”and the entropy dynamics looks like a Page curve.Cited from Ref.[3].

以下问题值得注意:1)首先现在的计算对于相当一大类相互作用费米子体系都是正确的,即类似Page 曲线的熵变规律并非是有引力对偶的模型的特有特征,而很有可能是非常一般性的普适规律;2)初步理论测试的成功让我们可以更加细致地研究在不同时间点上量子力学侧发生的物理现象,同时通过引力对偶的假说映射回引力体系来看在黑洞蒸发问题中的一些物理细节,甚至包括在黑洞内部的物质状态的细节;3)微扰的更高阶效应所产生的物理效应也是非常值得关注的.

值得一提的是,同时间Dadras和Kitaev[52]也创始了这种一般性的对熵的微扰线性响应方法,并计算了一些高阶的微扰效应.后来苏凯翔等[53]也计算了SYK4和SYK2 之间的耦合造成的熵变.他们的计算利用了SYK4 的可解性质和replica 技术,能给出长时间的熵变结果,因此对于环境和系统的耦合强度没有限制.

5 总结与展望

本文综述了可以用于一般相互作用系统与一般环境在弱耦合情况下的线性响应理论,这一理论包括了原来没有被计入的耗散造成响应动力学.文中给出了系统性的展开和用图形学方法来计算的技术.回顾了这种方法在用于非厄米线性响应动力学中与量子临界现象的研究,以及利用线性响应的技术如何来计算熵的变化.为了展示计算效果,在有引力对偶的模型中模拟“黑洞蒸发”的过程,发现了类似Page 曲线的熵变曲线.值得一提的是,由于本文的方法可以绕过对密度矩阵在耗散动力学过程中的直接计算,而仅仅和初态下的关联函数有关,因此大大简化了耗散动力学的计算,同时让我们可以有能力去计算一些强相互作用的开放系统的动力学.这些计算在过去都是比较困难的.同时还发现,在本文微扰方法的高阶贡献中有超越原先主方程的贡献,可能对于理解多体耗散动力学等有新的帮助.