基于平面相控阵的轨道角动量涡旋电磁波扫描特性*

蒋基恒 余世星 寇娜 丁召 张正平

1) (贵州大学大数据与信息工程学院,贵阳 550025)

2) (贵州大学,贵州省微纳电子与软件技术重点实验室,贵阳 550025)

3) (贵州大学,半导体功率器件可靠性教育部工程研究中心,贵阳 550025)

轨道角动量涡旋电磁波可以在物理层面为信息的调制提供新的维度,这在无线通信和雷达成像领域中拥有很大的应用前景.将相控阵波束扫描技术应用于涡旋电磁波,可用于增加涡旋电磁通信的覆盖范围,也可用于扩大涡旋雷达的探测空域.首先,本文讨论了涡旋电磁波束偏转的实现原理,并给出了实现波束扫描时平面相控阵口径上所需的相位分布公式.其次,考虑到相控阵天线在波束扫描以及轨道角动量模式可重构方面的独特优势,设计并制作了一款阵面规模为8× 8 的平面相控阵,并在10 GHz 频率下实验验证了轨道角动量涡旋电磁波的波束扫描和模式可重构效果.最后,本文讨论并分析了涡旋电磁波束偏转后的性能变化.仿真和实验结果显示,平面相控阵在大角度波束扫描时会发生方向图畸变的问题.同时,本文还研究了涡旋电磁波的模式纯度关于波束偏转角度和模式数的变化情况.本文的研究结果表明,使用平面相控阵天线在一定空域内可以有效地实现涡旋电磁波束扫描,并可为涡旋电磁波通信和涡旋雷达提供参考借鉴.

1 引言

随着无线通信技术的飞速发展,大数据和云计算等领域的数据传输速率呈指数级增长,如何提高无线通信系统容量和无线频谱利用效率已成为当务之急.携带轨道角动量(orbital angular momentum,OAM)的涡旋电磁波的提出被认为有望解决这一问题,它可以在不增加频带带宽的前提下,在同一频率、同一信道中同时传输多个互不干扰的正交模式,这为信息的调制提供了新的维度[1].OAM涡旋电磁波的特征在于有一个形如exp(ilφ)的波前相位因子,其中φ是极坐标下的方位角,l是OAM模式数[2].与传统电磁波不同的是,OAM 模式数l可以任意取值,且不同模式具有相互正交的特性,因此利用OAM 模式数进行编码和复用,相比于传统通信技术,能极大提高频谱利用率[3].与此同时,有研究显示OAM 涡旋电磁波可以提高雷达成像的分辨率,因而OAM 在雷达领域也具有重要的应用前景[4-6].近年来,关于OAM 涡旋电磁波的相关研究发展十分迅速,特别是在微波频段方面的研究已成为热点话题.如何才能高效地产生OAM涡旋电磁波是研究者们广泛关注的一个关键问题.目前,研究者们已提出了多种天线用于产生OAM波束,如螺旋相位板[7]、螺旋反射面[8]、环形天线阵[9,10]、行波天线[11,12]、介质谐振天线[13]、平面透射阵[14,15]、平面反射阵[16-18]、以及人工电磁超表面[19-22]等.然而,现有文献报道的涡旋电磁波天线,产生的大多为法向波束,以及偏转方向固定的波束[23].随着涡旋电磁通信和涡旋雷达技术的发展,将实时动态的波束扫描技术引入OAM 涡旋电磁波是发展的必然趋势[24,25].平面相控阵天线[26]作为一种较为成熟的技术,具有结构简易、剖面低、波束相位调控灵活等特点,已广泛应用于雷达和无线通信系统中,因此将其用于涡旋电磁波束的扫描具有一定的可行性.本文基于8×8 规模的平面相控阵天线,对涡旋波束偏转进行了定性分析,研究了平面阵列在偏转角度以及模式数变化时所产生的涡旋波束特性,相关研究结果可为未来涡旋雷达和涡旋电磁通信提供理论支持.

2 涡旋波束扫描原理以及OAM 模式纯度计算

2.1 涡旋波束扫描原理

如图1所示,当OAM 涡旋电磁波束的指向为任意角度(θ,φ)时,可以通过坐标旋转变换设置一个相对直角坐标系X′Y′Z′,使得波矢k的方向与Z′轴重合.在此条件下,用平面阵天线生成OAM 波束,平面阵上各单元的相位Φ可表示为

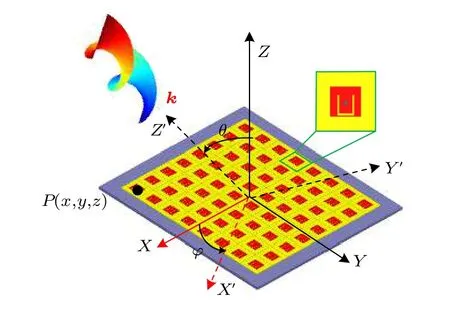
图1 用于产生涡旋电磁波的平面阵列天线示意图Fig.1.Schematic diagram of the planar array for generating vortex waves.

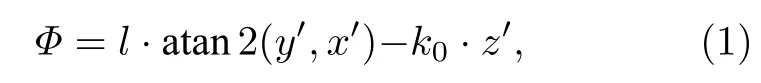
其中atan2(y,x)是四象限反正切函数,值域为[0,2π];l是OAM 模式数;(x′,y′,z′) 为天线单元在相对坐标系中的坐标位置.(x′,y′,z′) 与(x,y,z) 之间的关系可以通过坐标系旋转建立,具体表示为

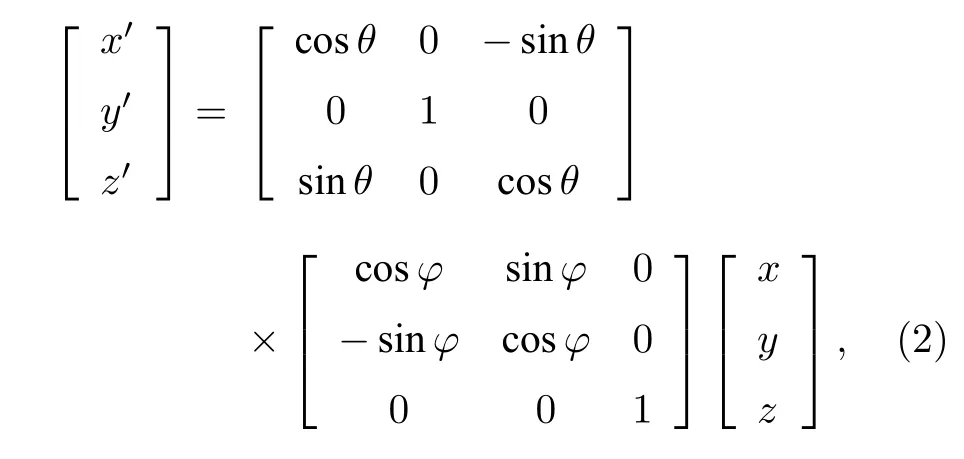
其中全局坐标系XYZ先围绕Z轴旋转角φ,然后围绕Y′轴旋转角θ.最后,可以得到:

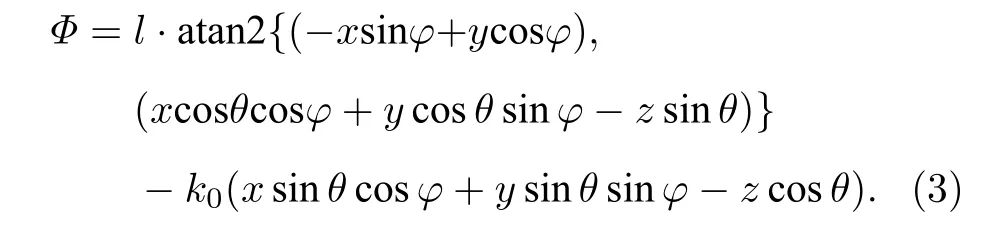
2.2 OAM 模式纯度计算

我们可以利用傅里叶变换进行模式分解,分别以涡旋波束的相位奇点为圆心,沿主波束选取一个环形电场数据,并对其进行傅里叶变换即可得到该波束对应的OAM 谱[27].其计算公式为

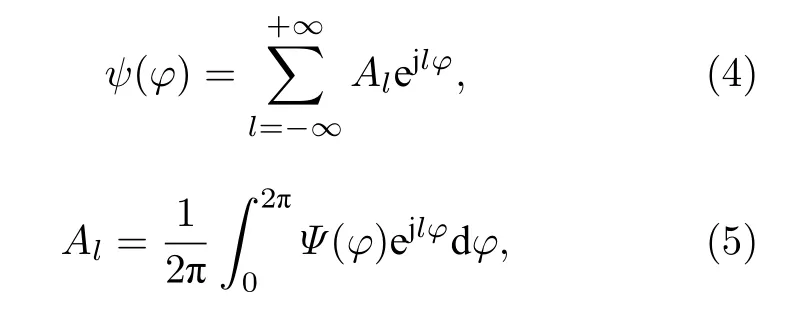
其中其中ψ(φ) 是以Z轴为轴线的圆周上的相位,模式l的模式纯度为[28]

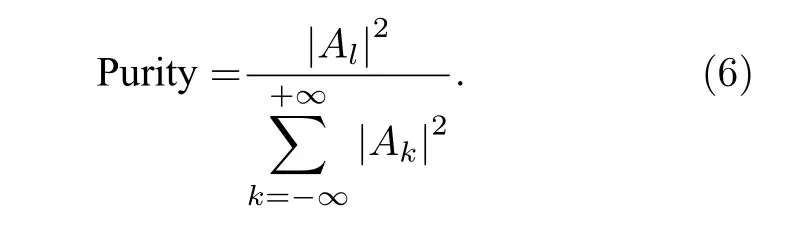
通过电场观测面测量出的OAM 波前电场的幅度和相位信息,运用以上公式计算出模式数l下的纯度.

3 仿真与实测分析

为了验证所提出的理论方法,通过三维电磁场仿真软件对8×8 平面阵列产生OAM 涡旋电磁波的情况进行了定性分析.选定φ=0°,θ从0°扫描到75°,模式数为l=1,2,3.通过模拟仿真,取出各偏转角度和各模式数下的相位分布和幅度分布,算出轨道角动量涡旋波的模式纯度,如图2所示.在扫描角度θ≤40°时l=1,2,3 模式均能保持较高的模式纯度,当扫描角度大于40°时随着模式数的增加模式纯度的衰减速率也随之变大,在θ从0°变化至75°的过程中模式纯度最低为55%以上,模式l=2 在θ从0°变化至70°的过程中模式纯度最低为60%以上,另外模式l=3 在θ从0°变化至60°的过程中模式纯度最低为50%以上.图3显示了在固定OAM 模数l=1 的情况下,当θ=0°,30°,45°,60°和75°时所产生的OAM 涡旋波束的3D 方向图.由图3可以分析出,在l=1 模式时,当扫描角度大于60°时,方向图会出现很明显的畸变和增益降低等问题.

图2 模式数为l=1,2,3 时各OAM 模式的纯度随偏转角度变化的情况Fig.2.OAM purity vary withangle of deflection with l=1,2,3.

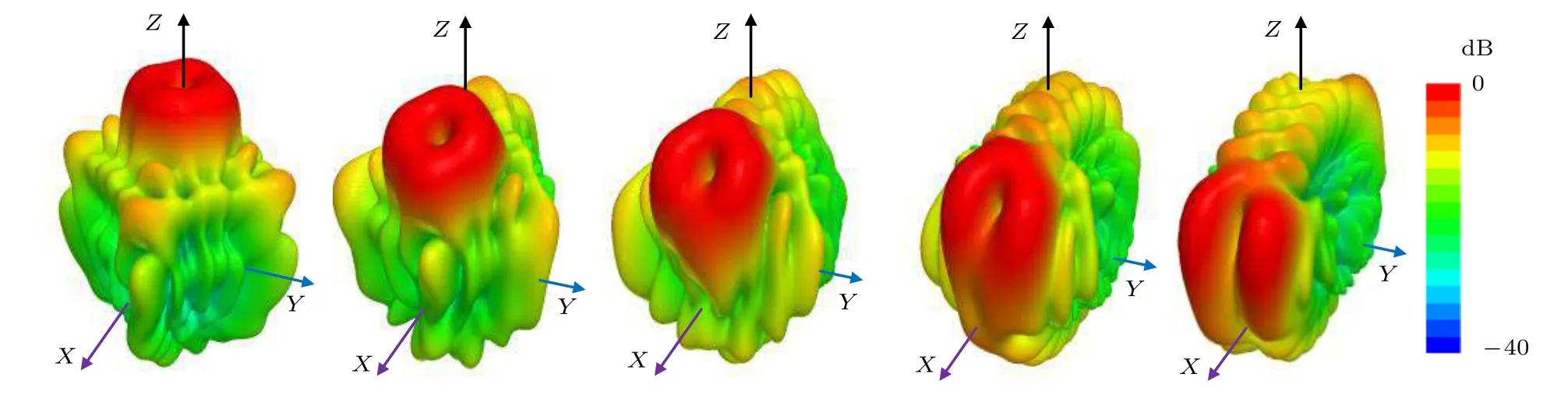
图3 仿真三维远场方向图 (l=1),(θ,φ)=(0°,0°),(30°,0°),(45°,0°),(60°,0°) (75°,0°)Fig.3.Simulated 3-D far-field radiation patterns,(l=1),(θ,φ)=(0°,0°),(30°,0°),(45°,0°),(60°,0°) (75°,0°).

为了进一步验证所提出的理论分析方法,制作尺寸大小为160 mm×160 mm×15 mm 的平面天线阵列.天线单元印刷在旺灵的F4B 基板上(εr=2.65,tanδ=0.001),并组装在3D 打印的聚乳酸(PLA)材质支撑结构上.天线单元连接至馈电网络,所需的相位通过馈电网络中的数字移相器芯片(Qorvo TGP2109-SM)控制.利用近场平面扫描技术测量了OAM 涡旋波束的波前相位,测量系统的工作频率为10 GHz.实验装置如图4所示.

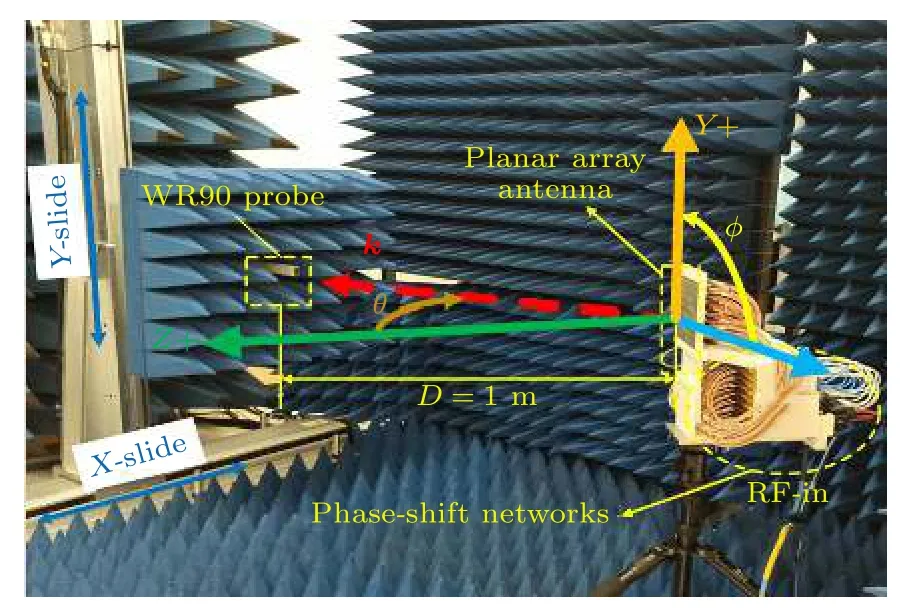
图4 利用近场扫描技术测量OAM 涡旋电磁波的实验装置Fig.4.Experimental setup for OAM wave measurement with near-field scanning technique.

首先,固定天线,将矢量网络分析仪(VNA)的端口1 通过射频同轴线连接至天线阵的射频总输入端(RF-in),采样平面距天线1 m,采样面的尺寸为0.8 m× 0.8 m(56× 56 个采样点),在测量装置的采样面上使用开口波导探头(WR90)通过射频同轴线连接至矢量网络分析仪的端口2 采集待测天线的数据,其数据包括电场幅度和相位数据.通过测试系统中内置的近远场变换算法,还可得到待测天线远场辐射特性.

通过计算机控制移相网络,调节每个单元的所需的相位.依次给天线单元馈电,生成θ=0°,30°,40°,50°,60°方向的OAM 涡旋波束.这里选择了OAM 的三种模式l=1,2,3 来验证设计.仿真和实测下的电场强度和相位分布如图5所示.

值得注意的是,考虑到近场扫描测试系统是固定的,这里通过旋转天线来匹配波束切换.在图5展示的仿真和实测的电场强度和相位分布中,整体上可以看出所激励的OAM 模式的电场的幅度只能在一定的θ角上保持较高幅度值.从测量和仿真的结果可以看出,在θ=0°,30°时,所测模式数的OAM 波束的电场相位和幅度分布是完整的环形.当扫描角θ大于30°时,测出OAM 波束的电场分布逐渐出现波纹,尤其是当偏转角θ变大时.而随着偏转角度增加和模式数增加波前相位和幅度分布出现畸变.从图5(a)—(d)可以清晰地识别模数为l=1,l=2 仿真与实测符合较好.在模式数l=2时,从相位分布也看出中心处也出现相位混乱,随着偏转角度的增加混乱情况越来越明显.在模式数l=3 时的相位分布来看,其有多个相位奇点,但是OAM 波束的中心区域为零深区域,也就是说其电场分布很弱,对通信系统来说并不会有影响.其实OAM 波束的辐射作用主要集中在电场幅度很强的区域.因此在提取OAM 涡旋电磁波的模式纯度时,是根据幅度大的区域为整个OAM 涡旋电磁波主导作用的原则提取.如下文图7中当模式数l=3时,在提取出的模式纯度中占比最高的模式恰好是l=3.随着偏转角度的增加,相位图的中心区域变得越来越混乱,另外从电场幅度变化情况看出,随着模数的增加,OAM 束的散射更大;随着偏转角度的增加,OAM 波束的散射也更大.确切说,零深区域的面积随着模式数和偏转角度的增加而增大.

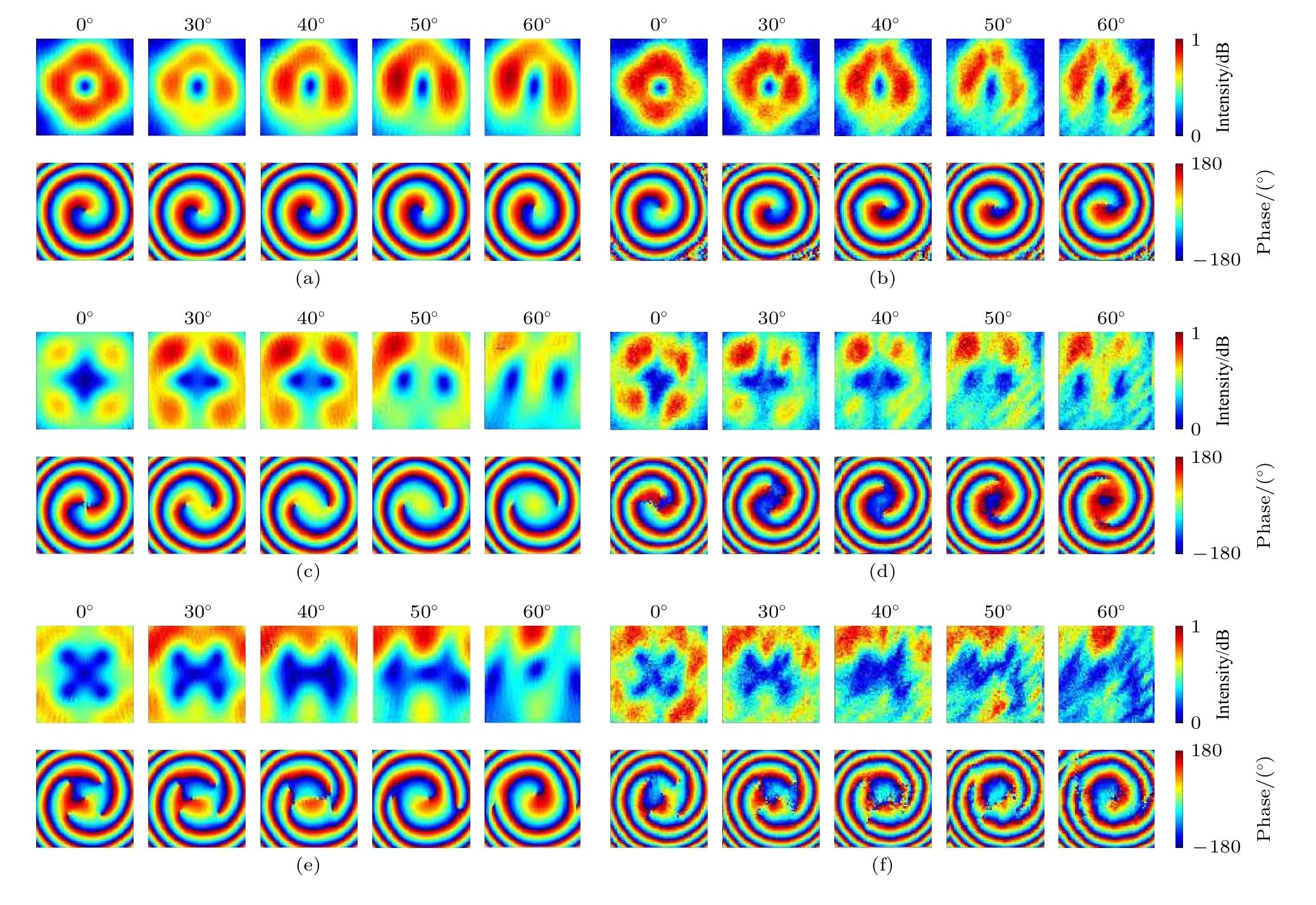
图5 幅度和相位分布 (a) 仿真l=1;(b) 实测l=1;(c) 仿真l=2;(d) 实测l=2;(e) 仿真l=3;(f) 实测l=3Fig.5.Phase and amplitude distributions:(a) Simulated l=1;(b) measured l=1;(c) simulated l=2;(d) measured l=2;(e) simulated l=3;(f) measured l=3.

为了更好地探索主波束畸变的情况,仿真与测量各模式数下的远场辐射方向图对比如图6所示.测量的方向图是通过平面近远场反演变换得到的,从仿真与实测结果看出低模式数时实测与仿真的方向图比较吻合.在OAM 波束的远场方向图中,中心场点处的场强为零,出现零深现象.随着模式数增加和偏转角度增大方向图的零深区域逐渐变大,零深深度逐渐减小,其原因是采用平面阵列天线在偏转角度变大时产生OAM 波束,其有效口径也会逐渐变小,相当于用于产生OAM 波束的天线单元数也会变少.由于一定天线单元数量的阵列可以产生的最大OAM 模式数是有限的,所以随着扫描角度的增大,有效口径的减小,其所能产生的最大OAM 模式数越来越小.因此,随着偏转角度的增加,当产生的一定模式数的OAM 波束均突破有效口径所能产生的最大模式数,就会造成模式纯度下降和波束畸变等问题.另外实测出现较明显的波纹是由于安装误差和环境噪声影响造成的.

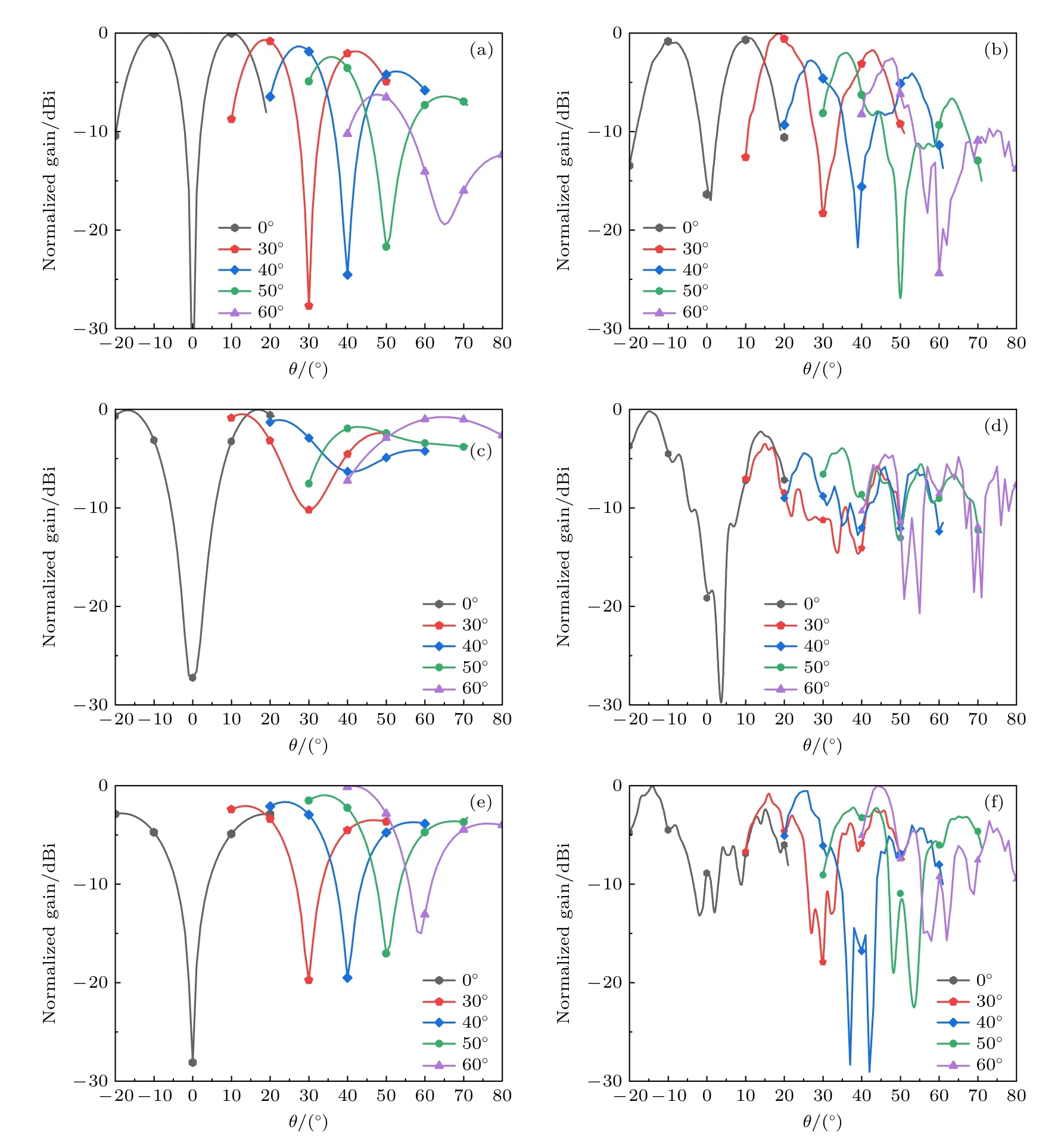
图6 XOZ-平面上的远场仿真与实测结果 (a) 仿真l=1;(b) 实测l=1;(c) 仿真l=2;(d)实测l=2;(e)仿真l=3;(f) 实测l=3Fig.6.The simulated and measured radiation patterns ofthearray in XOZ-plane:(a) Simulated l=1;(b) measured l=1;(c) simulated l=2;(d) measured l=2;(e) simulated l=3;(f) measured l=3.

最后,从仿真和实测出的场数据中提取相位和幅度数据,运用(6)式计算出各模式的纯度大小,将OAM 涡旋电磁波仿真与实测的模式纯度进行对比如图7所示.在l=1,2,3 时波束偏转从0°到60°模式纯度仿真与实测趋势基本一致,实测的模式纯度略低于仿真.其中模式l=1,2 偏转到60°时纯度接近50%,模式3 偏转到50°时纯度接近50%.仿真与实测结果表明随着模式数增加OAM波束逐渐发散,随着扫描角度增加进一步促使OAM波束加速发散.

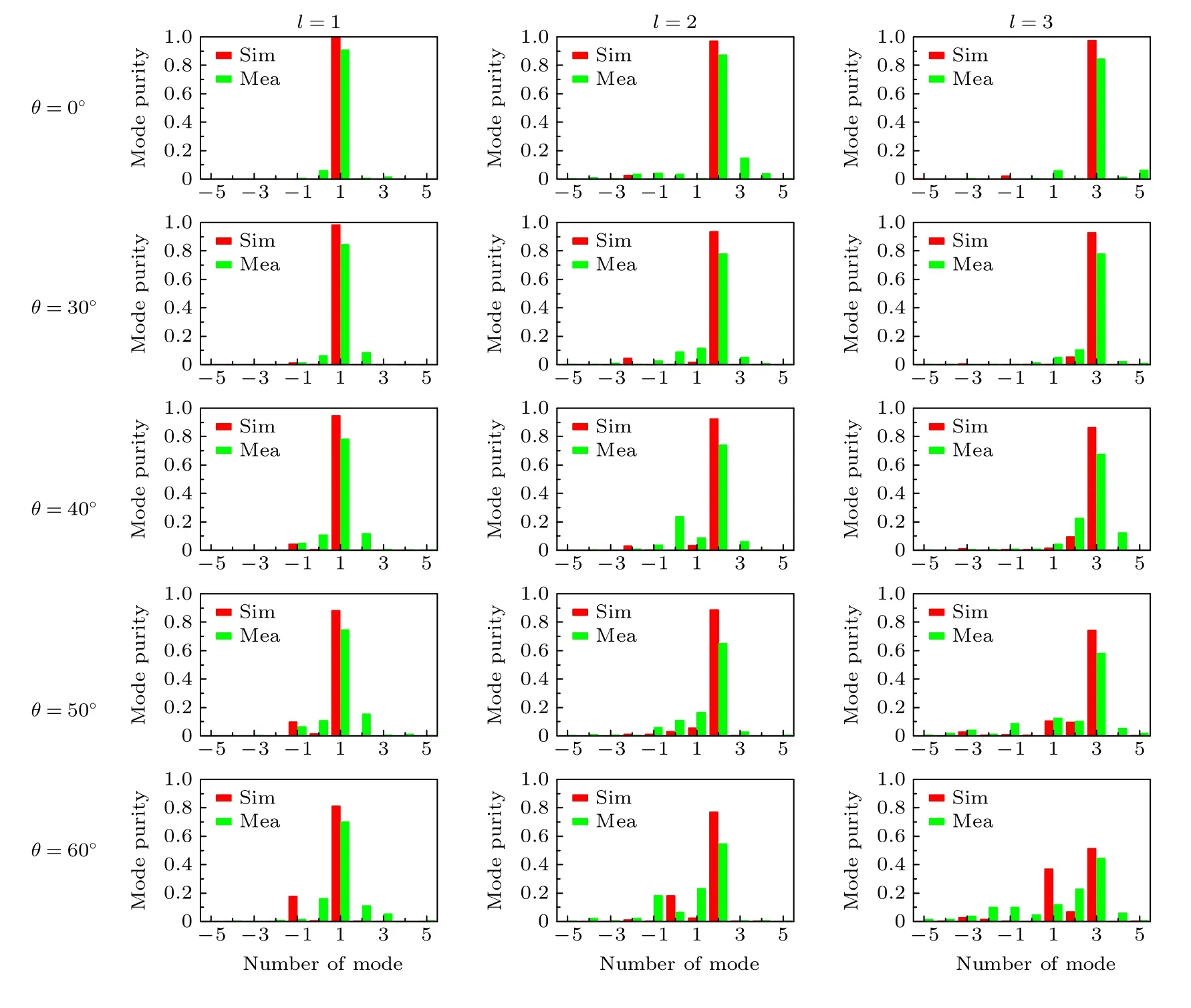
图7 各模式数下随扫描角度变化的仿真与实测模式纯度对比Fig.7.OAM purities of different modes and scanning angles.

4 结论

本文讨论了使用平面相控阵天线进行OAM涡旋电磁波波束扫描的实现方法,通过仿真和实验研究了10 GHz 频率8× 8 规模的平面相控阵天线,在不同OAM 模式在不同角度偏转时的性能变化问题.OAM 涡旋电磁波在偏转时,随着模式数的增加其电场能量会发生一定的横向扩散,电场中心的空洞会逐渐扩张,导致模式纯度逐渐降低,同时随着扫描角度增加进一步促使涡旋波束加速发散.本文验证了平面相控阵天线可以在一定角域范围内产生较高OAM 模式纯度的涡旋电磁波,相关结果可为未来涡旋雷达和涡旋电磁通信提供参考借鉴.