基于SKUA的浅层三维地质建模方法与实例研究

杜 睿，杨歧焱

DU Rui, YANG Qi-yan

河北地质大学 京津冀城市群地下空间智能探测与装备自然资源部重点实验室 河北省战略性关键矿产资源重点实验室，河北 石家庄 050031

Hebei GEO University, Shijiazhuang 050031, China

0 引言

传统的勘察技术及数据处理手段单一，得到的二维矢量图（平面图、剖面图）不能直观、准确、清晰地表达地下地质情况。三维地质建模是在三维环境中，利用计算机软硬件系统，对空间中的地质数据进行采集、处理、解释并与地学统计、空间分析、地质地层预测、三维可视化等相关工具结合起来，并用于地质方面分析的一门技术[1]。20世纪80年代，已有学者开始对三维地质建模进行研究，Haldorson提出了随机模拟储层建模[2]方法和Calson E地下结构有关的三维概念模型[3]，A.B.Ekoule解决了三维物体非凸轮廓线的重建问题[4]；Bak、Smith等提出了一些三维模型和地学信息的三维表示[5]。直到90年代初“三维地质建模”的概念才被加拿大学者Simon W.Houlding正式提出[6]；之后，针对地质数据本身具有的不确定性和不连续性的特点，Mallet提出了“离散光滑插值”算法[7,8]，使得构造建模技术的地质曲面技术得到了突破，美国T-surf公司设计基于离散光滑插值算法研发了GOCAD（Geological Object Computer Aided Design）三维地质建模软件；随后，Carl Youngman（1990），Molenaar Marien（1991），Fritsch D，AaperJ.F（1992），Molenaar M，TurnerA.K（1992），Thomas R.Fisher（1993），Rongxingli（1994），Lattuada R（1995），DekempE.A（1999；2003），HerbertM J（2001），Saini-Eidukat B（2002）等人又进行了大量的研究，主要包括三维数据的可视化、数据的空间模型与空间结构、矢量化地图的三维数据结构等方面[9-11]；2006年GOCAD被加拿大Paradigm公司收购；2007年Paradigm公司推出SKUA-GOCAD，也称为SKUA（Subsurface Knowledge Unified Approach，SKUA）软件；2011年Paradigm公司进行二次开发，将SKUA集成到Epos数据库平台上（Paradigm公司内部资料），推出了可以建立任何复杂地质模型（地层、尖灭、断裂等）的SKUA软件，为三维地质建模理论的发展做出了贡献。

1 空间插值拟合

由于工程钻孔价格昂贵，能获得的有用钻孔较少。因此通常需要对原始采样数据进行插值拟合。所谓插值就是指满足某种变异函数的前提下，寻找有限区域已知离散数据附近的拟合点，从而在整个研究区范围内生成足够多的连续、分布均匀的数据点[12]。由于不同的插值方法有不同的适应条件，本文考虑到样本点和待估点之间的位置关系，还考虑到待估点之间具有的空间相关性，拟采用普通克里金插值和离散光滑插值。

1.1 克里金插值

克里金（Kriging）计算权值的方式是通过引入一个以距离为自变量的半变差函数来实现，确定权值后即可确定待测值点的位置，从而确定待测点处的最佳线性估计值[13]。克里金插值考虑了所有观测点的空间分布结构特点，与传统插值方法相比，其插值结果更接近实际情况[14,15]。

其算法如下：设xi（i=1，2，…，n）为空间数据点的坐标，zi（i=1，2，…，n）表示其对应的观测值。对于某点x0处的值记为Z（x0），则Z*（x0）可用克里金插值公式

权重λi由方差最小和无偏性估计来唯一确定一组λi值：

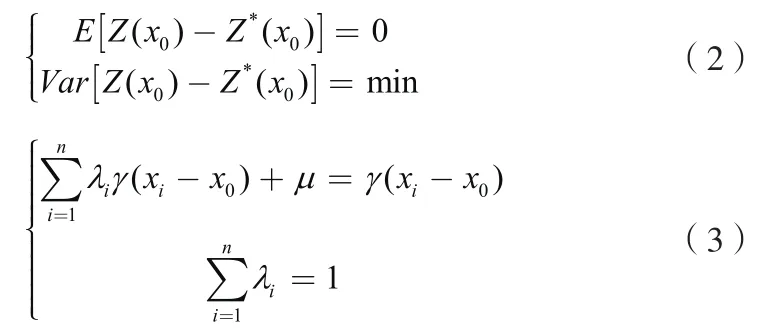
本文利用确定出的权值进行克里金插值计算，多次试验后发现普通克里金插值能够很好地拟合研究区地质信息的变化规律，并对准确估计未知点变量。

1.2 离散光滑插值

离散光滑插值（Discrete Smooth Interpolation，简称DSI）是Mallet教授针对CAD平面制图软件在地质构造数据内插上的不足提出的，其基本内容是：首先建立一个相互联系的自然体网格，然后利用网格结点的邻接关系，完成从已知结点函数值到未知结点函数值的估算[16]。离散光滑插值作为SKUA的特色插值技术，在SKUA软件的构造建模和速度建模中得到了成熟的应用。

现将DSI算法的理论基础简述如下：

假设G=G（S）为曲线多边形，Ω=Ω（S）为曲线多边形上的顶点集合，N=|Ω|为在Ω上的点，φ（k）为定义在k∈Ω上的函数，只在Ω的子集上φ（k）为已知的，φ为一个n维列矩阵φ=[φ（1），（2），…，φ（n）]T。

为了方便讨论，将φ矩阵分为矩阵φI和φL（其中φI为已知矩阵，φL为未知矩阵）。

首先，要找出R*(ϕ) =R(ϕ) +ρ(ϕ) = min的φ（k）函数（其中，R（φ）为全局粗糙度，ρ（φ）为线性约束），并利用φ（k）函数对曲面进行估计。

a.粗糙度

R（φ|k）是局部粗糙度，R（φ）为全局粗糙度

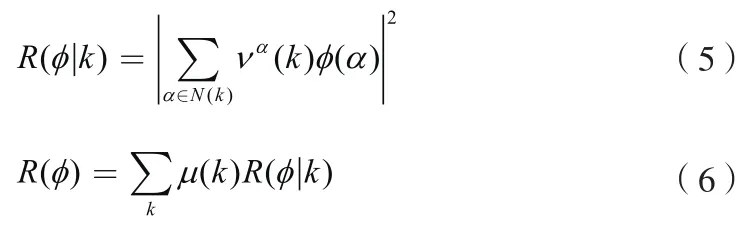
式中，{να(k)}为给定的权系数，其值为整数；

N（k）为节点k的邻域；

μ（k）在Ω上给定的非负权函数。

从上述式中可以得到R（φ）是根据{να(k)}和μ（k）确定的。

b.最小平方的线性约束ρ（φ）

对于n维矩阵Ai和一个常数bi，定义有：

c.问题解决

由φ（k）函数（k∈Ω）插值所组成的值域中确定出使R*(ϕ) =R(ϕ) +ρ(ϕ)值最小的一个数，然后将R*(ϕ)展开有：

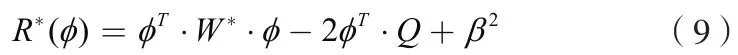
式中，W*为对称半正定矩阵，Q为列矩阵，β2为非负系数。

其中，

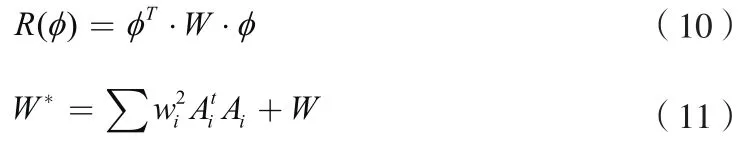
依据上述分析把φ矩阵划分为φI和φL两个矩阵，能够得到矩阵W*和矩阵Q两个矩阵。

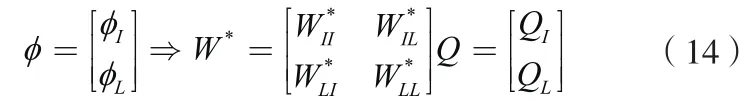
综合分析上面的数学求解过程，可以知道离散光滑插值（DSI）的基本思想是找出一个φ（k）函数使R*（φ）达到最小值，其值完全依赖于权函数{να(k)}和μ（k）的取值，其中II方阵秩的唯一性决定了DSI插值法解的唯一性。

2 建模思路

三维地质建模主要分为两类：一类是构造和地层（Structure & Stratigraphy modeling）建模，适用于钻孔数据较为丰富的区域，构造和地层模型能够表达地层面和断层面的位置和相互关系，能够直接观测到地表的跌宕起伏；另一类是三维储层栅格结构[17]（3D Reservoir Grid Building）建模，适用于高光谱遥感图像、数字高程图像等方法的区域性建模。储层建模能反映地质体的物性参数，如岩石的渗透率、孔隙度等。其中构造建模是储层建模的基础，本文采用SKUA软件和构造建模为主阐述快速三维地质建模基本流程。

2.1 建模原始资料

本文在沧州市高新区某工程区10.2 km2的范围内，根据工程的实际需要，收集的数据情况如下（表1）。理论上讲，钻孔的间距越小数量越多、工程地质剖面图越详细、对区域地质的认识越深入，越有利于地质建模工作的开展[18]。

表1 沧州市某工区建模数据一览表Table 1 List of modeling data for a work area in Cangzhou city

2.2 钻孔数据库的建立与导入

本文以60张钻孔柱状图，10张工程地质剖面图为原始数据，依据地震反射同相轴分层的原则将地层分为4层。首先将图、表等数据导入EXCEL整理后导入ArcGIS，进行坐标转换，转换成功后导出坐标系并保存为SKUA-GOCAD能够直接导入的TXT格式。SKUA-GOCAD软件对钻孔数据的录入格式如下：井轨迹包含钻孔编号（WellName）、测深（MD）及坐标（X，Y，Z）等5列数据；钻孔测斜表包括钻孔编号（WellName）、倾角（Dip）、方位角（Azimuth）、测深（MD）、分层名称（Markername）等5列数据[19]。数据导入之前最好对数据进行全面排查，尤其是小数位数，正负号等，避免建模过程产生各种意想不到的误差。

钻孔数据导入SKUA过程如下：（1）导入井轨迹数据：Import→Well Data→Paths→column-Based File→选择Wellpath数据→Next→选中X-Y-TVDSSMD→选中Meter→选中Use a column→Next→为每列匹配相应的参数；（2）导入钻孔测斜表：Import→Well Data→Markers→column-Based File→选择Markers数据→Next→选中By column→Next→选择有无MD和Dip and Azimuth→Next→选中Overwrite it→Next→为每列匹配对应的参数。

2.3 建立点模型

原始点模型的建立可以直接用井分层文件来建立。也可以用各个地层面的点数据来建立，过程如下：PointsSet→New→From Well Markers→Locations→选中所有的井文件→选择相应的Marker’s feature→Name。由于钻孔信息提供的原始数据点较少，为了快速准确的进行建模需要进行空间插值，本文分别对每一层的原始数据点进行克里金插值，以A3层为例，插值前后效果如下图1所示

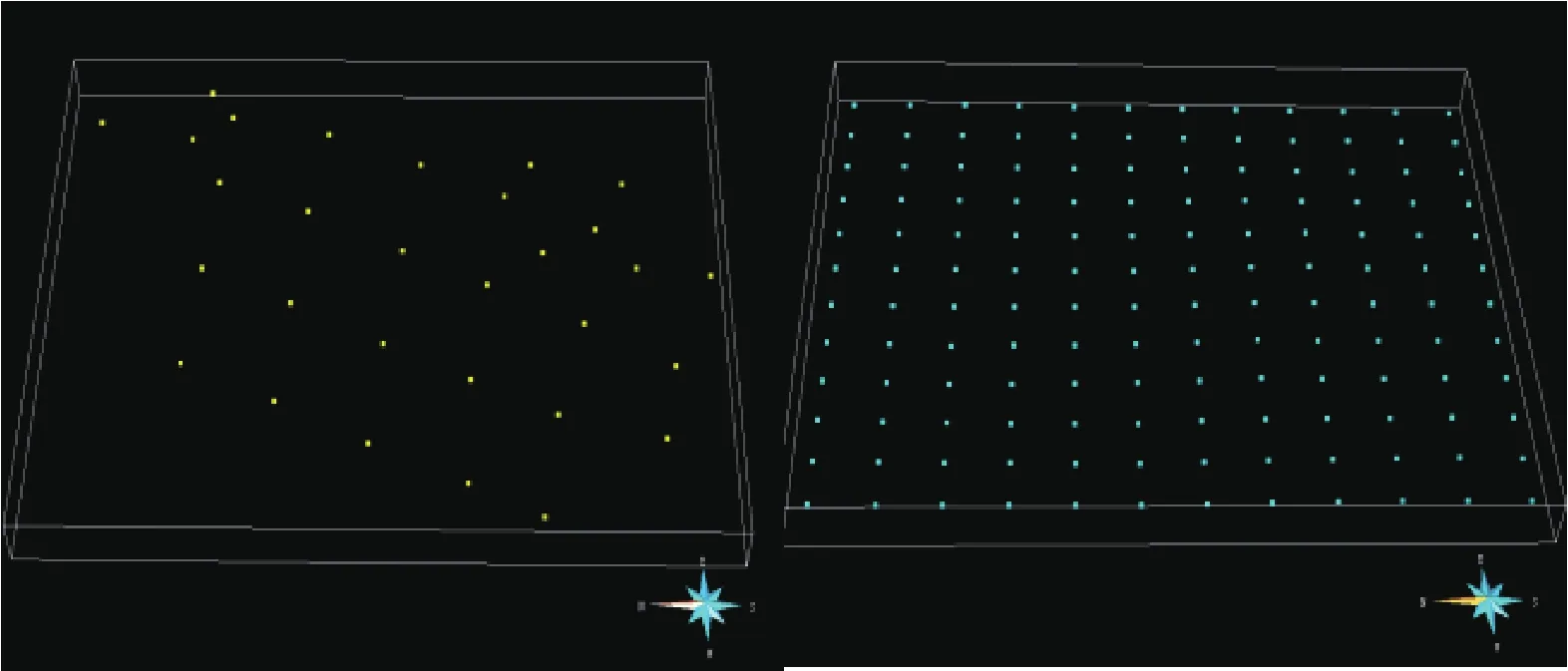
图1 （a） 原始数据点； （b）克里金插值后数据点Fig.1 （a）Original data points；（b）Data points after kriging interpolation

2.4 建立面模型

面模型是由点模型生成的，面模型不仅可以表现层面的高低起伏，还可以展现地质体结构和地质体形态，是构造建模中的核心部分[20]。过程如下：Surface→New→From PointsSets→PointsSet→选择相应的点文件，SKUA会自动给Surface命名与点文件同名的名字，点击apply生成面模型（图2（a））。

从图3中的面模型可以看出，部分插值点与地层面存在不一致的情况，尽管克里金插值优于其他算法，但它们都有一个共同的缺点，插值数据生成的曲面与原始控制点并不完全一致[21]。为此，SKUA软件在DSI理论的基础上提供了一种几何适应（fit geometry）的功能，它可以将插值曲面与不在曲面上的控制点进行重新匹配，从而不断修正几何畸变，得到更加符合实际的曲面。操作过程如下：Surface→Constraints→Control Points→Set Control Points→选择相应的地层面和控制点→点击Fit Geometry，多次重复，直到控制点完全落在层面上（图2（b））。

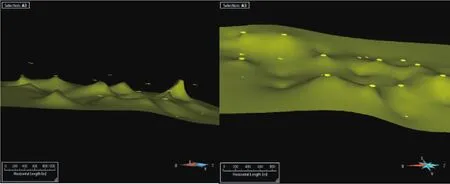
图2 （a）由插值数据生成的面模型； （b）几何适应后的面模型Fig.2 （a）Surface model generatedby the interpolation data；（b）Surface model after fit geometry.

2.5 建立构造模型

点击Structure & Stratigraphy→选择深度域→选中所有的地层→然后建立地层柱→选中所有的well→Check Data Consistency→Next→定义感兴趣的区域（感兴趣的应大于最顶层和最底层的高度）→Next→选中所有的地层→Preview。建立地层之前先预览各层面，预览地层面时可以进行如下操作：1）逐层建立层面，忽略不一致的数据点；2）检测是否存在交叉层面；3）根据剖面图对层面局部区域进行微调。预览后再Build All建立各地层→Compute Paleo-coordinates→Next→Building the Geologic Grid→Compute Unit Areal Extension→Compute Unit Thickness，最小单元不同和厚度不同均会影响计算效率，本文根据推荐采用的Cell size为39.822 m，Set Number of Cells为10。Build Geologic Grid建立地质格网如图3。

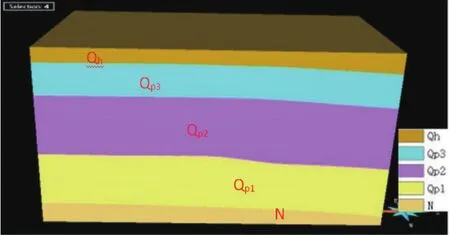
图3 研究区三维地质构造模型Fig.3 3D geological structure model of the study area

2.6 地质剖面与解释剖面做对比

地质剖面是地质图件的一种。它是沿地球表面某一方向的假想垂直面与地形相切得到的剖面图，称为地质剖面图[22]。它能直观地反映出剖面方向、地形及地层的厚度、岩性、断层和倾角等信息。其操作如下：General→Cross Section→选择构造模型→New→From Digitized Polyline→从左往右任意画一条线，生成的剖面如图4（a）。

图4 （a）地质构造模型剖面图； （b）某测线地震反射时间剖面Fig.4 （a）Geological structure model profile view ；（b）Seismic reflection timeprofile of a seismic line

随机从该工程区三条地震测线中取出一条，其测线剖面如图4（b），从地震勘探地质解释剖面上可以看出，该测线有多组较强的反射层位，比较明显的反射层在90 m、150 m、260～300 m、400～420 m的深度，推测其分别为T1、T2、T3、T4。将图4（a）与图4（b）对比可知，构造模型剖面与任意一条测线的剖面大致相吻合，构造模型较好。

3 总结

本文提出了在地层情况较为简单，但钻孔数据不足的情况下，结合空间插值拟合技术进行快速建模的方法。针对沧州某工区插值后的控制点进行几何适应，去除离群值，几乎都能落在层面上，插值效果较好，建模方法简便快捷，可以广泛应用于工程地质、油气开发、地质灾害治理、地球物理勘探等领域，与二维平面图相比能提供一种更直观的表现形式。但是，三维地质建模相关理论和软件在国内地质领域应用还较少，有不少复杂问题还需进一步研究。