基于MATLAB的液压伺服系统位置控制仿真分析

刘　锐

基于MATLAB的液压伺服系统位置控制仿真分析

刘锐

(湖南信息职业技术学院，湖南 长沙 410200)

在分析IGV系统的组成和原理的基础上，搭建了IGV系统液压模拟试验台。根据液压模拟试验台相关部件的参数，在Simhydraulics中搭建了仿真模型。用最小二乘参数辨识方法对所搭建的仿真模型进行系统辨识，得出系统的传递函数。根据系统传递函数的特性，设计了优化的PI控制器，并利用MATLAB进行仿真分析。结果表明，所设计的控制器能够保证液压伺服系统具有良好的位置跟随性，并且具有一定的抗干扰性能，满足实际工作条件。

液压伺服系统；位置控制；PI控制器；IGV

1　引言

随着现代工业的迅速发展，电液比例控制已经广泛应用于能源电力、机械制造和冶金工业中精度要求较高的工程实践里。在上述这些行业中应用的很多液压设备都能实现较高的位置控制精度。例如，在用于燃气—蒸汽联合循环的重型燃气轮机中，为了扩大压气机的稳定工作范围，提高联合循环效率，常常在压气机的第一级动叶之前设计一列进口可转导叶(Inlet Guide Vane, IGV)。液压伺服系统位置控制的快速、准确和稳定是IGV系统正常工作的必要条件。由于采用由电液比例阀控制液压缸组成的闭环控制系统能够实现精度要求较高的位置控制，因此对其进行研究有着重要的现实意义。

针对GE公司PG9351FA型和三菱公司M701F4型燃气轮机中的IGV液压调节系统，在Simhydraulics仿真平台上搭建了物理模型。利用参数辨识的方法对物理模型进行系统辨识，得到系统的传递函数，利用MATLAB/Simulink进行仿真分析，研究优化的PI控制器，并对系统进行校正。

2　系统的组成和原理

在PG9351FA的IGV系统中，每一个IGV叶片的顶部都安装了一个小齿轮。这些小齿轮的转动由两个半圆的齿条带动；齿条的动作由油动机HM3-1来操纵。这样，就可以通过油动机的动作来改变IGV的安装角。

如图1所示，燃机启动时，来自OH-4的高压液压油经过滤器FH6-1后流向伺服阀90TV-1和进口可转导叶遮断阀VH3-1。由于跳闸油在启动转速继电器14HT动作前(>15%转速动作)是无压状态，所以遮断阀VH3-1在左边弹簧力的作用下处于左位。液压油经VH3-1进入油动机HM3-1的油缸活塞下腔室。活塞上腔室经VH3-1接通回油管路OD。此时，油动机活塞移到顶部，使IGV处于初始状态的最小开度，即28.5°。

图1　压气机IGV系统图

当机组在变频启动装置的牵引下启动并使14HT动作时，形成跳闸油压，推动VH3-1阀向左移动并使该阀处于右位。这时，将液压油OH-4接通伺服阀90TV-1和油动机之间的液压油路，使IGV处于可调整状态。位置信号LVDT(96TV-1，-2)用于IGV开度的调节反馈[1]。

将阀控液压缸简化，所设计的IGV液压调节系统模拟平台如图2所示。图2中，IGV位置调节系统包括IGV系统液压源、三位四通伺服阀、工作液压缸和油箱等，系统工作液压缸油压为3～4MPa。液压负载输出系统包括负载系统液压源、三位四通伺服阀、负载液压缸、油箱、力传感器和位移传感器等，系统负载液压缸油压为1～2 MPa。

图2　IGV液压调节系统模拟平台

3　基于Simhydraulics建立系统物理模型

3.1　系统的主要参数

将工作油泵的油压设定为3MPa；双作用液压缸的行程是200mm；弹簧质量阻尼系统中：kg，1000N/m，N/(m/s)。

3.2　系统的物理模型

通过对图2的分析，在Simhydraulics中建立IGV液压调节系统模拟平台的仿真模型，如图3所示。

图3　IGV液压调节系统模拟平台仿真模型

整个物理模型由输入部分、控制部分、执行部分、数据采集和显示部分组成。其中，输入部分模拟的是IGV系统实际工作过程中的指令信号；控制部分采用的是PI控制器，通过三位四通换向阀控制双作用液压缸的行程位置；执行部分是一个双作用液压缸，液压缸的负载由一个弹簧质量阻尼系统来模拟；数据采集和显示部分使用位移传感器，对双作用液压缸的位置进行测量，采用示波器显示数据，可分别显示指令位置、实际位置以及实际位置与指令位置的误差三项内容。

3.3　阀控液压缸的系统辨识

为了分析系统的行为特性、理解系统的运动规律、设计系统的控制策略，通常需要了解系统的数学模型。多数情况下，系统的数学模型并不可知，或者数学模型的参数会随着系统运行环境的变化而变化。通过测取系统在某些输入信号作用下的输出响应，或者是记录正常运行的输入输出数据，经过必要的数据处理和数学计算，估计出系统的数学模型。利用系统辨识的方法建立的数学模型一般是系统输入输出特性在某种准则意义下的一种近似，近似的程度取决于人们对系统先验知识的认识和对数据集合性质的了解以及选用的辨识方法[5]。

对系统辨识的方法有很多，其中应用最广泛、辨识效果良好的是最小二乘辨识法。应用最小二乘法对系统模型参数进行辨识的方法有离线辨识和在线辨识两种。离线辨识是在采集到系统模型所需全部输入输出数据后，用最小二乘法对数据进行集中处理，从而获得模型参数的估计值。根据式(2)搭建物理仿真模型，可以采集到系统的输入输出数据，采用最小二乘法进行离线辨识，得到系统的传递函数，如图4所示。

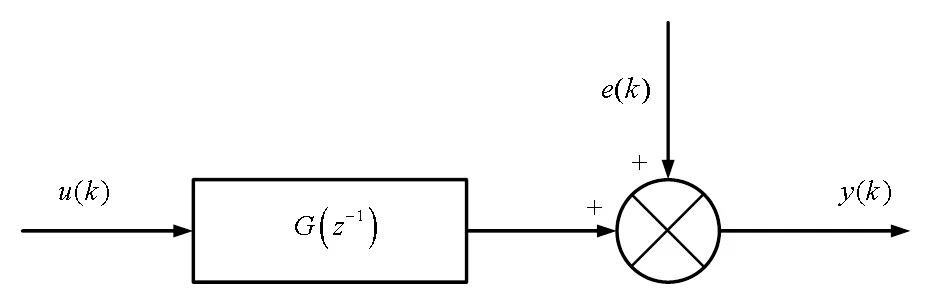
图4　SISO系统结构图

系统的离散传递函数为：

系统输入输出的关系为：

结合(1)式和(2)式可以得到：

其中：

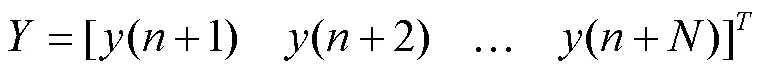
那么，由此得到最小二乘估计为：

根据最小二乘参数辨识法，系统的传递函数为：

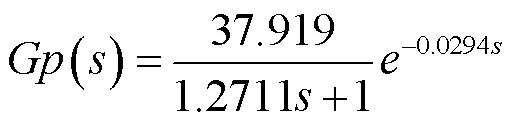
4　优化PI控制器及系统仿真分析

4.1　设计优化PI控制器

系统控制结构如图5所示。

图5　系统控制结构图

在普通PI控制系统中加入内层反馈，根据自动控制原理相关知识，等效系统传递函数为：

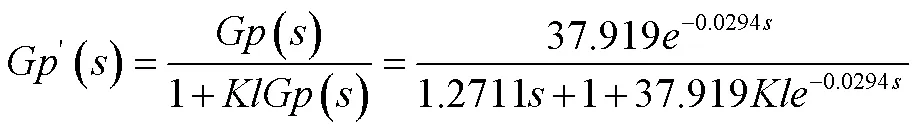
分母用泰勒级数展开：

结合以上的分析，所设计的PI控制器为：

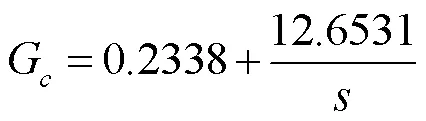
将图5变简化为图6所示的结构：

4.2　系统仿真分析

设定仿真时间为20 s，选择求解器ode14x。

仿真结果显示：当IGV系统的指令位置如图8所示的时候，根据图7所示的误差曲线可以看出，系统的超调量为0，误差小于3%，满足系统的要求。

图7 IGV系统模拟工况下的误差

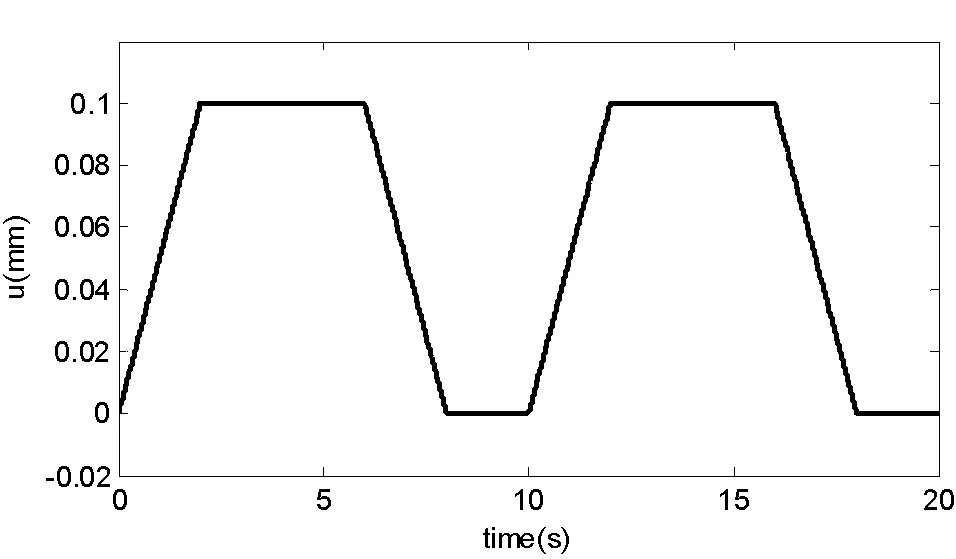
图8　IGV系统模拟工况

系统的阶跃响应表示系统的抗干扰性能。当系统输入为幅值0.1的阶跃信号时，相应误差曲线的和响应曲线如图9和图10所示。

从图9和图10可以看出，系统具有相对较好的抗干扰特性。系统在受到突发扰动时能够快速地回到稳态，并且稳态误差为0。

图9　IGV系统仿真模型阶跃响应误差

图10　IGV系统仿真模型阶跃响应

5　结论

在分析GE公司PG9351FA型和三菱公司M701F4型燃气轮机中的IGV液压调节系统的基础上，搭建了IGV系统液压模拟实验台。目的是设计一个优化的PI控制器，从而提高液压伺服系统的位置指令跟随性。搭建了基于Simhydraulics的物理仿真模型，并利用最小二乘参数辨识的方法求得系统的传递函数。在此基础上，设计了优化PI控制器。从仿真结果可以看出：在IGV系统工作指令的情况下，最大相对误差不到3%；系统在干扰存在的情况下(采用阶跃信号模拟系统的干扰)，稳态误差为0，超调量为0，上升时间为0.1270 s。系统的性能完全符合实际工作要求。

[1] 孙益科. PG9351FA型燃气轮机进口可转导叶的控制[J]. 制冷空调与电力机械,2008,29(5):78-82,85.

[2] 赵士杭.燃气轮机结构[M].北京:清华大学出版社, 1983.

[3] 王春行.液压控制系统[M].北京:机械工业出版社, 2011.

[4] 清华大学热能工程系.燃气轮机与燃气:蒸汽联合循环装置(上)[M].北京:中国电力出版社, 2007:56-95.

[5] 萧德云.系统辨识理论及应用[M].北京:清华大学出版社,2014.

[6] ZHAO Y G, JIA L, CAI W J. The system identification and PID auto-tuning for unstable processes[C]//2008 3rd IEEE Conference on Industrial Electronics and Applications. June 3-5, 2008, Singapore. IEEE, 2008: 176–180.

[7] SKOCZOWSKI S, DOMEK S, PIETRUSEWICZ K, et al. A method for improving the robustness of PID control[J]. IEEE Transactions on Industrial Electronics, 2005, 52(6): 1669–1676.

[8] WANG Y G, SHAO H H. Optimal tuning for PI controller[J]. Automatica, 2000, 36(1): 147-152.

Simulation analysis of hydraulic servo system's position control based on MATLAB

LIU Rui

(Hunan College of Information, Changsha, Hunan 410200, China)

Based on analyzing the composition and principle of the IGV (Inlet Guide Vane) system, in this paper, an IGV system's hydraulic simulator stand is built. According to the parameters of the relevant units in the hydraulic simulator stand, a simulation model was built in Simhydraulics. To estimate the unknown parameters of the system, the least square parameters estimation method was employed. As a result, we can get the transfer function of the plant. According to the characteristics of the system transfer function, the optimization of the PI controller is designed and simulated analysis with MATLAB. Results show that the optimized PI controller can help the hydraulicservosystem following the instruction very well. And with the optimized PI controller, this system has certain anti-interference performance, and can meet the actual working conditions.

hydraulicservosystem; position control; PI controller; IGV

TP273

A

2096–8736(2021)03–0028–05

刘锐(1992—)，男，江西赣州人，硕士研究生，工程师，主要研究方向为机电液一体化技术、机械设计及仿真分析。

责任编辑：阳湘晖

英文编辑：唐琦军