斜坡桩-土动力p-y曲线的简化计算方法——以西南地区某典型碎石土场为例

陈 峰

(1.福州市建筑科学研究院有限公司 福建福州 350000；2.福州市建筑工程检测中心有限公司 福建福州 350000)

0 引言

线路工程往往需穿越山地、丘陵等斜坡场地，其坡度普遍较陡，2008年汶川8.0级和2013年芦山7.0级地震，给地区的线路工程造成一定程度的损坏。这其中，80%以上为地基基础(桩基础)的地震震害所导致。

地震作用下桩基础的计算，主要采用时程分析法和振型分解反应谱法。振型分解反应谱法适用于大多数地震作用下桩基础计算分析，采用时程分析法更适用于需精确计算或高烈度地震工况[1-3]。一直以来，国内外学者对于承受水平作用的桩基础研究较少，多数研究往往偏重于竖向作用下桩土的工作特性。研究主要集中在动力方程的求解、动力响应试验、动力特性参数等方面[4-6]。Boulanger[7]基于理论分析、室内离心机试验、数值模拟实现了可用于液化场地桩-土动力相互作用的p-y单元。Knappett[8-9]将p-y曲线关系式嵌入ABAQUS数值平台，开展了桩基动力响应研究。Zheng[10]为了探究桥梁工程中场地液化如何影响桩基础力学性能，创造性地给出了地震作用下，桩-土-结构相互耦合方法。Wu[11]基于quasi-3D FEM方法结合PILE3D、PILE-PY对砂土中桩基动力响应进行了分析并计算动力p-y曲线。Liu[12]、Wilson[13]均在离心机试验基础上提出砂土动力p-y曲线，并发现其动力p-y曲线与砂土初始密度的相关关系。总之，动力p-y曲线的建立需反映桩-土的耦合作用，往往采用较为复杂的土的本构模型，计算中参数选取难度大，且需要通过较为精密的室内试验得到相关计算参数，难免缺乏实用价值。动力p-y曲线法实为一种折衷方法，介于简化分析方法与复杂分析方法之间，具有计算精度高、易与数值手段结合等优势，还能准确反映桩和土的材料非线性、桩-土耦合作用。该方法能很好地分析地震作用下桩-土动力相互作用问题。

本文以某一线路工程为例，采用有限元软件FLAC3D建立三维边坡模型，详细分析4种边坡坡度条件下，斜坡桩基地震过程中桩身位移y与桩侧土体水平抗力的相关关系。然后结合API曲线理论，推导斜坡场地碎石土p-y曲线简易计算公式。

1 工程概况

该线路工程位于Ⅷ度地震烈度区，穿越地形坡度为30°，如图1所示。场地下伏第三系层状砂岩，节理发育。上覆第四系坡残坡积碎石土，粒径一般为3 cm～8 cm，棱角状，磨圆度差，块石之间充填少量黏性土，厚3 m～5 m。

该线路工程所用基础为混凝土人工挖孔桩基础。桩径1.0 m，桩长10.5 m，出露0.6 m。混凝土等级C25。

图1 线路工程所穿越的斜坡地形图

2 模拟方案

根据场地、地基条件，以及桩基础方案，采用FLAC3D建立计算模型。模型长(y方向)357 m，宽290 m(x方向)，最大高度150 m，最小高度17 m，所建立的模型，如图2所示。为了分析边坡坡度对桩基础地震响应的影响，坡度考虑为0°、15°、30°、45°。

图2 计算模型

(1)计算参数选取：建模过程中，桩基础实际尺寸采用柱型网格(即六面体网格)进行建模。通过网格节点，连接上部结构和桩周土体。上部结构采用空间梁单元模拟[14]。表1给出了岩土体详细取值参数。

表1 物理力学参数表

(1)边界条件确定：模型顶部为自由边界、底部为固定约束、地震作用下四周为自由边界；

(2)动力计算中材料阻尼的设定，本文采用瑞雷阻尼，可由刚度矩阵K和质量矩阵M表示：C=αM+βK。式中：α、β为瑞雷阻尼系数。

其中：ωi、ωj分别为结构的第i和第j振型的固有频率，ξi、ξj为相应的阻尼比。一般情况下，i、j分别取1和2[15]。

(3)地震荷载选取芦山地震名山科技，强震动台数据，仅考虑水平地震作用。通过SeismoSignal进行人工滤波，处理后的地震波时长30 s，计算步长0.005 s，历时8 s～18 s左右为振动峰值区，地震主震频率为10 Hz。波形图如图3所示。计算时，将加速度时程从基底输入，相当于施加于研究对象所有单元上，从相对运动角度来看，认为是对象不动而是基岩作反向运动。

图3 地震加速度时程曲线

3 计算结果分析

3.1 动力p-y曲线

图4为基准模型不同桩深桩-土体系动力p-y曲线图。地震作用下土的应力-应变关系呈现显著的非线性。选取所经过的拐点或极值点作为该滞回圈的顶点，并假定此点为骨架线上的点。

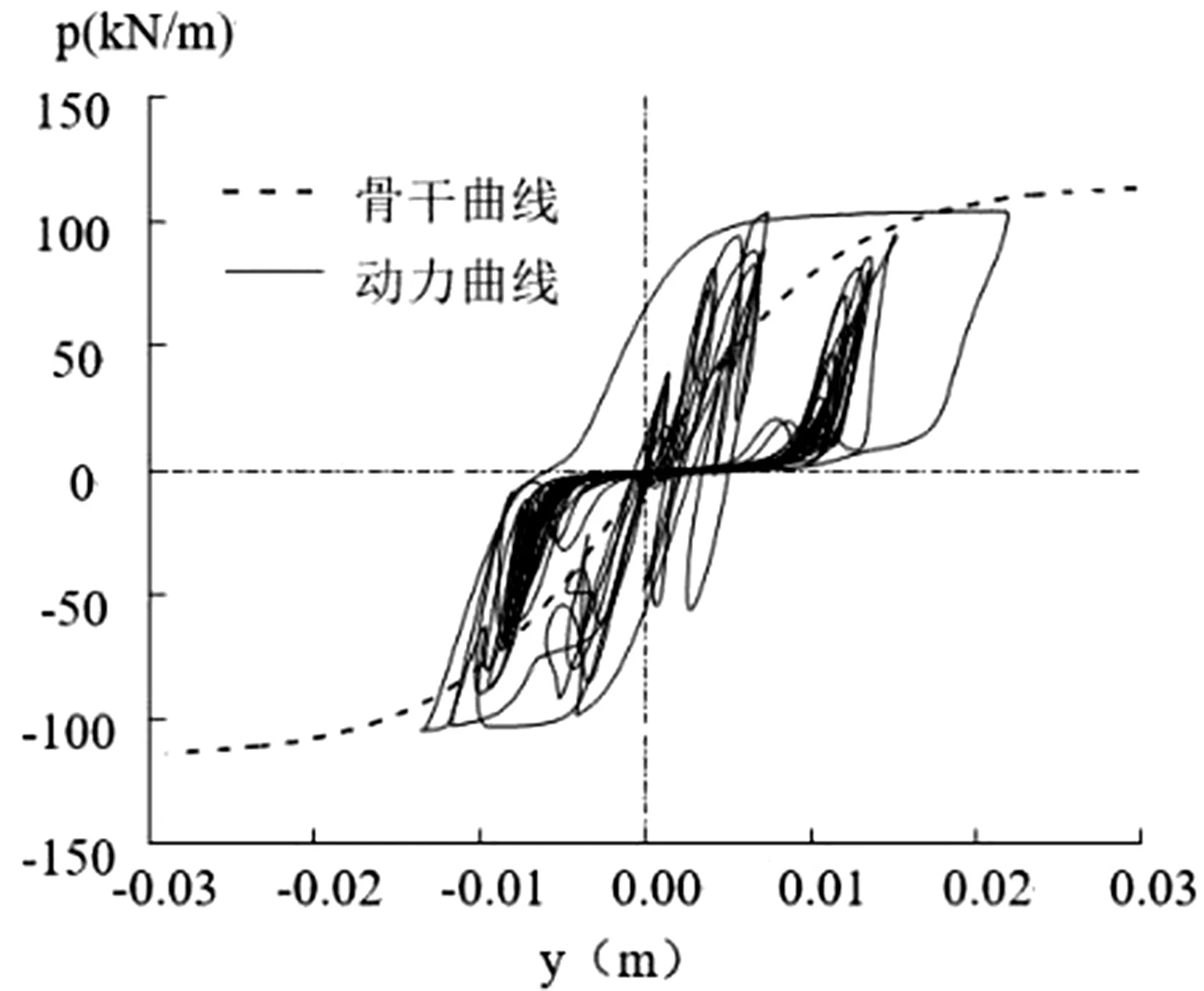
(a)桩深1 m

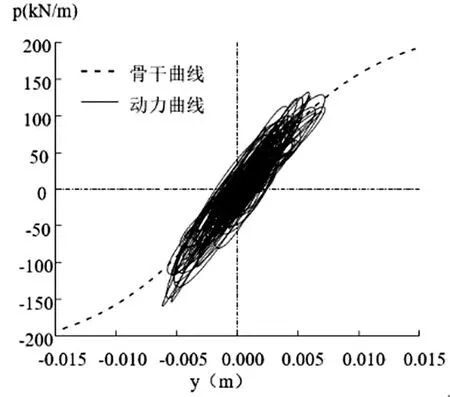
(b)桩深3 m

(c)桩深5 m

(d)桩深7 m图4 不同桩深桩-土体系动力p-y曲线

从图4中可见，碎石土动力p-y骨干曲线的形状为上“凸”型。从振动初期至振动结束过程中，p和y从成正比例变化，逐渐呈现步调不一致，尤其对于浅表层土体两者不一致性表现得十分明显。这一现象说明，斜坡场地桩身上部土体易出现大变形而丧失抵抗强度。另外，p-y曲线随着埋深的增加，土体刚度(kini)逐渐变大，土反力(pu)增大，滞回圈面积(S)却在减小，说明桩-土相互作用动力耗能作用，随深度增加而逐渐增大，但滞回圈形式近似相似。

3.2 斜坡坡度对动力p-y曲线影响

进一步整理不同坡度下，桩-土体系动力p-y骨干曲线初始模量(kini)、极限土抗力(pu)与坡度(β)关系，其中初始模量(kini)为最大土体抗力与之相对应的位移之比。图5、图6分别为坡度β对地基土体初始模量kini影响曲线、坡度β对桩侧土体抗力pu的影响曲线。

图6 坡度β对桩侧土体抗力pu的影响

如图5所示，针对模拟所得的结果，获得了四种不同坡度时p-y曲线地基土体初始模量，分别为0°、15°、30° 和45°(模型中桩径1 m，桩长10.5 m)。结果显示，坡度β与地基土体初始模量kini的关系如式(1)。当桩埋深超过7 m后，坡度对地基土体初始模量kini无显著影响，不同坡度下的计算结果与0°坡度计算结果一致。在坡面至7 m范围内，kiniβ/ki0比值随深度近似线性递减。

(1)

式中：δ为kiniβ/ki0比值，其中kiniβ为坡度β时地基土体初始模量，ki0为水平场地地基土体初始模量；z为计算深度；d为桩径。

图6给出了坡度β对桩侧土体抗力的影响规律。结果显示，每一坡度下的puβ与水平场地下pu比值近似为常数，斜坡坡度对puβ/pu值有影响，桩深对其影响不明显，坡度0°，15°， 30° 和 45°时，其比值分别为1，0.789，0.634和0.5。其关系如式(2)：

(2)

式中：puβ为坡度β时桩侧土体极限抗力，pu为水平场地地基桩侧土体极限抗力。

4 动力p-y曲线简化计算方法

4.1 API曲线理论

p-y曲线可以很好地考虑土体的非线性、各项异性，适用各类土体，能够描述静力非线性对桩基水平向承载力的作用。前面已经提到了各种经验公式，其中以API(American Petroleum Institute)[16]提出的公式应用最广。API曲线基本计算公式如式(3)-式(5)。

pus=(C1z+C2d)×r×z

(3)

pud=C3×r×z×d

(4)

(5)

式中：pu-地基极限承载力，取公式3和4两者最小值(pus为浅基础，pud为深基础)；γ-土体有效重度；z-计算深度；Φ-土体内摩擦角；C1，C2，C3-与土体内摩擦角有关系数，如图7所示；kini-地基土体初始模量；y，d-z深度内桩身位移及桩径。

图7 C1、C2、C3与土体内摩擦角关系

4.2 简化计算方法构建

斜坡动力p-y曲线的建立，不仅要反映出土体在线弹性阶段力与位移之间的相互关系，同时还要能体现塑性阶段土的变形特征。结合数值模拟获得的地震荷载条件下，碎石土动力p-y曲线，以保持主要特征和曲线形式一定的前提下，忽略加载路径的影响，考虑斜坡坡度与p-y骨干曲线关键参量之间的相互关系，满足建立的动力p-y曲线简化模型的数值，易于体现、数学表达式尽可能简易、特别关注场地斜坡坡度、桩入土深度对p-y曲线的影响。将式(1)、式(2)引入API经典曲线，从而建立动力p-y曲线的经验公式。

(6)

其中，kini如公式1计算，则忽略了土体阻尼对运动的影响。因其计算方法为最大土体抗力与之相对应的位移之比。为了描述阻尼造成桩-土体系地震能量损失情况，Novak[17-18]通过一系列的原型和室内试验，获得一个衡量阻尼和能量耗损的表征指标，基于动力条件下，不同深度单位桩基极限土体抗力pmax与桩身位移y之间的关系，建立以频率为基本变量的阻抗函数用来表征静动p-y曲线斜率两者关系，其假定动力p-y骨干曲线斜率与桩-土体系阻尼效应造成的能量损失之和，即为静载条件曲线斜率，关系式如式(7)所示。

(7)

如前所述，滞回圈面积S可以明确反映震动过程中由于阻尼作用使桩-土体系产生能量的损耗情况，故将滞回圈面积S作为表述阻尼系数的主要参数，初步表示成式(8)。即每一级循环荷载下p-y曲线的滞回环的面积(S)，可代表这一级荷载下能量变化情况。其可表述为：

(8)

动参照图4，动力荷载滞回圈面积，按照椭圆形面积的计算方法进行整理：S=πab。可进一步建立S-ymax之间的关系，参考Emmanouil Rovithis[19]推导得出的体系阻尼系数与曲线滞回圈面积之间的关系，最终动力p-y曲线骨干曲线的地基土体初始模量kd：

(9)

式中：pmax—桩侧地基土体反力最大值；ymax—桩侧地基土体反力最大值对应的土体位移最大值；ω为激振频率。

故碎石土斜坡桩-土动力p-y曲线的简化计算方法可按公式(10)计算。

(10)

5 结论

本文针对斜坡桩基动力p-y曲线法分析地震大变形与大变位问题方面的缺失。以西南地区典型碎石土场地为例，采用FLAC3D有限元软件建立4种边坡坡度条件下的桩-土体系分析模型，详细分析不同斜坡坡度种桩基地震过程中桩身位移y与桩侧土体水平抗力的相关关系，结论如下：

(1)地震输入下非线性碎石土动力p-y曲线，相对规则、对称。随着埋深的增加，土体刚度逐渐变大，土反力增大，滞回圈面积减小；

(2)归纳出不同坡度下桩-土体系动力p-y骨干曲线初始模量(kini)、极限土抗力(pu)与坡度(β)关系表达式，从其引入API理论曲线中，推导了碎石土斜坡桩-土动力p-y曲线的简化计算公式；

(3)同时为阻尼造成桩-土体系地震能量损失的情况，建立以频率为基本变量的阻抗函数，以使所述的简化计算公式更合理。