基于计算思维能力培养的算法与程序设计教学策略

黄尚伟

在当今的信息社会中，培养和提高信息素养是对初中生的基本要求，而信息素养表现为个人对信息工具的应用以及处理信息和解决问题的能力，计算思维则包含了信息工具的使用和解决问题能力，所以计算思维的培养是初中生信息素养的一种体现。

● 利用算法和图形，落实学生的计算思维

1.借助流程图，直观表达解决问题思路

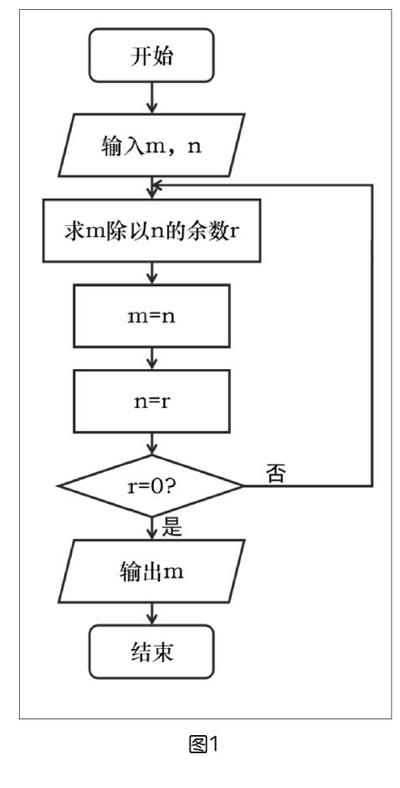
流程图是使用图形表示算法思路的一种直观方法。例如，面对求两个正整数m、n的最大公约数的问题，学生可以采用辗转相除法即欧几里德算法：对于任意两个自然数m和n，用m、n、r分别表示被除数、除数、余数，那么m和n的最大公约数等于n和r的最大公约数。即第一步求m除以n的余数r;第二步若r不等于0，执行第三步，若r等于0，则n为最大公约数，算法结束;第三步将n的值赋给m，将r的值赋给n，再求m除以n的余数r;第四步转到第二步。而利用流程图（如图1），能减少繁杂的文字，更加明确问题关键，提取问题特征，快速直观地表达学生解决问题的思路，最后借助编写程序解决问题。

2.培养学生算法思想，高效解决问题

计算思维是人的思维，是人求解问题的一条途径。针对需要大量计算的问题，引导学生在提出解决问题的方法后，理解计算思维涵盖的计算概念和方法，落实学生的计算思维。例如，递推问题“Fibonacci数列”：有雌雄一对兔子，假定过两个月便可繁殖雌雄各一的一对小兔子，过n个月后共有多少对兔子？“兔子繁殖问题”看似复杂，其实只需要清楚第x-2个月的所有兔子到第x个月都有繁殖能力就能解决问题。设满x个月共有兔子F（x）对，其中当月新生的兔子数目为N（x）对。第x-1个月留下的兔子数目设为F（x-1）对，则F（x）=N（x）+F（x-1），N（x）=F（x-2），那么F（x）=F（x-1）+F（x-2）。所以，由上面的递推关系可依次得到F（2）=F（1）+F（0）=1，F（3）=F（2）+F（1）=2，……。当n=90时，F（n）已经达到2880067194370816120。这样的问题如果没有计算机很难得知结果，所以，在培养学生算法思想的过程中，借助计算机有效落实计算思维，能够解决很多计算规模超大的问题。

3.使用思维导图，概括解决问题的算法

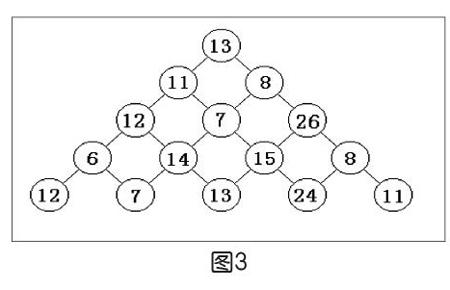
学生细化提出的问题解决方法，通过思维导图的使用（如下页图2），呈现出细化的方案，这种方法往往应用于难度系数较大的复杂题目。例如，设计五子棋的程序，其功能包括绘制棋盘、交替出现黑白棋、移动棋子、判断胜负等。学生利用思维导图能概括其学习的知识要点，清晰明了地组建知识网络，训练计算思维。

● 借助多种学习技巧，强化学生的计算思维

1.一题多解，多面思考

一题多解是指针对一道习题，能从不同角度去思考问题，寻找到不同的解题方法，并对这些不同解题方法进行总结和归纳。

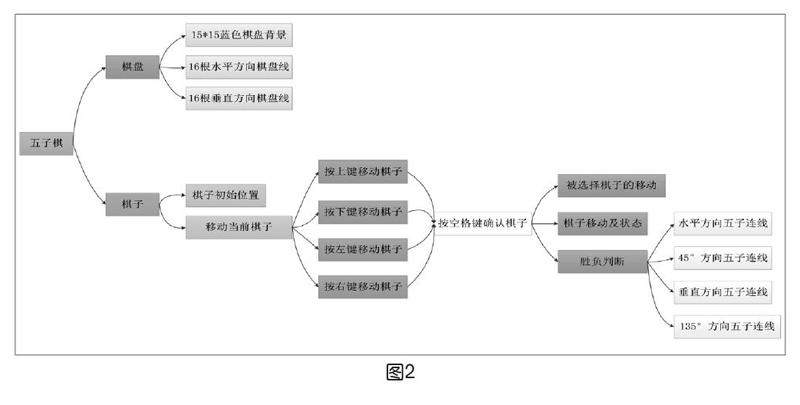
例题1：观察下面的数字金字塔（如图3）。写一个程序查找从最高点到底部任意处结束的路径，使路径经过数字的和最大。每一步都可以从当前点走到左下方的点，也可以到达右下方的点。

在上面的样例中，从13到8到26到15到24的路径产生了最大的和86。

输入：第一行包含R（1≤R≤1000），表示行的数目。后面每行为这个数字金字塔特定行包含的整数。所有的被供应的整数是非负的且不大于100。

输出：单独的一行，包含可能得到的最大的和。

样例输入：

5 //数塔层数

13

11   8

12   7    26

6   14    15    8

12   7    13   24    11

样例输出：86。

①方法一：搜索。问题要求从最高点按照规则走到最低点的路径的最大权值和，路径起点终点固定，走法规则明确，可以考虑用搜索来解决。

定义递归函数void Dfs（int x，int y，int Curr），其中x，y表示当前已从（1，1）走到（x，y），目前已走路径上的权值和为Curr。

当x=N时，如果Curr比Ans大，则把Ans更新为Curr;否则向下一行两个位置行走，即递归执行Dfs（x+1，y，Curr+A[x+1][y]）和Dfs（x+1，y+1，Curr+A[x+1][y+1]）（如下页图4）。

该方法实际上是把所有路径都走了一遍，由于每一条路径都是由N-1步组成，每一步有“左”“右”两种选择，因此路径总数为2N-1，所以该方法的时间复杂度为O（2N-1），超时。

②方法二：记忆化搜索。方法一之所以会超时，是因为进行了重复搜索。记忆化搜索需要对方法一中的搜索进行改装，需要记录從一个点开始到终点的路径的最大权值和，因此重新定义递归函数Dfs。

定义Dfs（x，y）表示从（x，y）出发到终点的路径的最大权值和，答案就是Dfs（1，1）。在计算Dfs（x，y）时考虑第一步是向左还是向右，笔者把所有路径分成两大类：第一步向左、第一步向右。

为避免重复搜索，笔者开设全局数组F[x][y]记录从（x，y）出发到终点路径的最大权值和，一开始全部初始化为-1，表示未被计算过。在计算Dfs（x，y）时，首先查询F[x][y]，如果F[x][y]不等于-1，说明Dfs（x，y）之前已经被计算过，直接返回F[x][y]即可，否则计算出Dfs（x，y）的值并存储在F[x][y]中（如下页图5）。

由于F[x][y]对每个合法的（x，y）都只计算过一次，而且计算是在O（1）内完成的，因此时间复杂度为O（N2），可以通过本题。

③方法三：动态规划（逆推法）。动态规划求解问题的过程归纳为：自顶向下的分析，自底向上计算。其基本方法是：划分阶段——按三角形的行划分阶段，若有n行，则有n-1个阶段。

图形转化：直角三角形，便于搜索——向下、向右。

用三维数组表示数塔：a[x][y][1]表示行、列及结点本身数据，a[x][y][2]能够取得最大值，a[x][y][3]表示前进的方向——0向下，1向右（如下页图6）。

2.一题多变，发散思维

一题多变，是指通过对一道习题，改变题目中的数据、所求的问题或题目中的条件，从而得到新的题目。一题多变的解题思路有利于学生思维的发散，并且能够使学生更加熟练地掌握多种解题思路和方法。

例题2：利用for循環，计算输出1+2+…+100的和。

例题3：利用for循环，分别计算1～100中奇数的和、偶数的和。

例题4：利用for循环计算n！=1*2*3…*n的值。

通过上述例题，可以让学生更好地理解和掌握这一题型。在学习过程中，学生运用一题多变的解题思路进行学习，从简单的题目入手，进行深入分析和研究。

3.一题多思，把握本质

一题多思，是指在“一题多变和一题多解”的基础上，面对同一种类型的题目，把握题目本质，从而快速解决问题。一题多思有利于学生思维的高度概括，并且能够更加有效地强化学生的计算思维。

例题5：成绩排序。给出班里某门课程的成绩单，请你按成绩从高到低对成绩单排序输出，如果有相同的分数，则名字字典序小的在前。

例题6：病人排队。病人看病需要登记，编写一个程序，将登记的病人按照以下原则排出看病的先后顺序：老年人（年龄≥60岁）比非老年人优先看病;老年人按年龄从大到小的顺序看病，年龄相同的按登记的先后顺序排序;非老年人按登记的先后顺序看病。

通过上述例题，可以让学生将算法思想从书本问题应用到实际生活问题的解决。

● 依托翻转课堂教学实践，渗透学生的计算思维

算法与程序设计教学的目的是培养学生的解决问题和计算思维能力。根据此教学目标，依托翻转课堂的教学形式，笔者在辅导学生的过程中设计了翻转课堂教学的三个基础环节，渗透计算思维。下面，以“结构体”教学为例谈谈具体过程。

1.课前推送信息，自主学习

教师根据知识点的难易程度，制作短小精悍的教学视频以及设计针对性的问题，并将其推送给学生，让学生进行提前学习，引导学生结合教学视频进行思考和解决，加强学生的自主学习能力。

例题7：成绩统计。输入N个学生的姓名和语文、数学的得分，按总分从高到低输出，分数相同的按输入先后输出。

输入格式：第一行有一个整数N（N≤100），下面有N行，每行一个姓名，两个整数。姓名由不超过10个的小写字母组成，整数范围为0～100。

输出格式：总分排序后的名单，共N行，每行格式——姓名  语文  数学  总分。

针对习题样例，设计了层层递进的针对性的问题（如表1）。

2.课堂内化知识，深度学习

在课堂中，教师需要结合课前的问题，通过讲授和演示、问题驱动教学方法促使学生深度学习，内化知识，完成教师的课堂教学目标和任务。通过小组讨论的教学方法，学生碰撞出对知识点更多的疑难问题，然后教师在课堂中进行解答和梳理，加强学生的深度学习。具体做法如表2所示。

3.课后巩固提高，归纳共性

课后要求学生完成课后习题来巩固所学的知识点，并让学生分析课后习题的共性，在分析的基础上，让学生尝试设计同类型的实际生活问题，将算法应用于生活，解决生活实际问题。

以上教学策略在实际教学中取得了一定的成效，但还远远不够。因此，在教学中如何更有效地培养和提高学生的计算思维能力，仍然是一个需要不断探讨的问题。