流程图中的抽象与建模

陈凯

查阅文献资料，可以发现“计算思维”这一名词时常和“抽象”“建模”等名词有密切的联系，或许相当多的老师认可这种说法：“运用计算思维来解决问题的过程中可能涉及到抽象、建模等方法。”但若反过来说“当解决某问题过程中用到了抽象、建模的方法，则体现出了计算思维的运用”，这样的观点就很值得怀疑了。那么问题是，在什么样的情况下，我们在解决问题的过程中用到了抽象、建模的方法，并且也能同时说，问题解决方案的产生运用到了计算思维？

● 用数学模型模拟日常事件

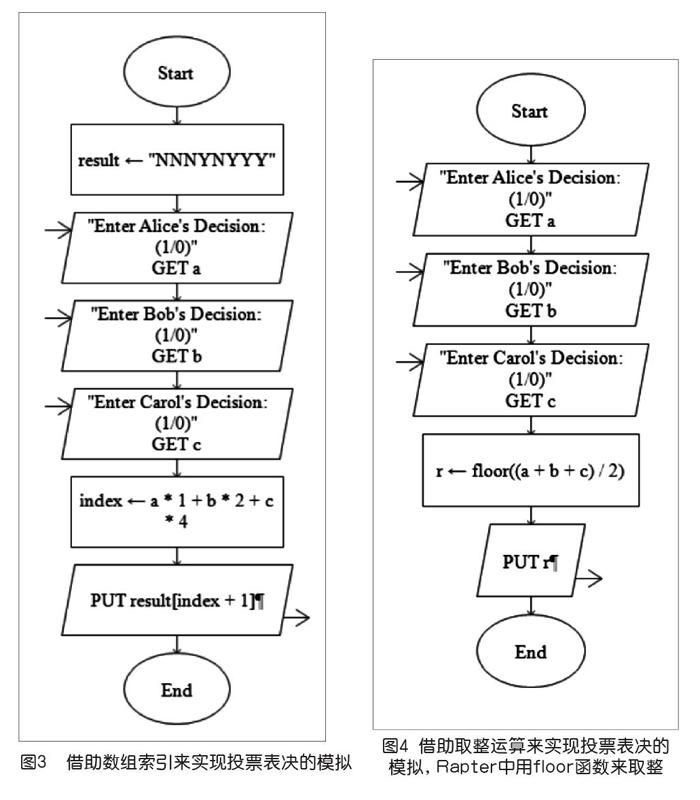
考虑现实中这样一个常见的简单问题：假设有三人通过举手投票来做出某个决定（如決定是玩还是学习？），每人1票，当多数人投赞成票，即有两人或两人以上举手时，某决定（那就去玩吧！）被通过。要求学生们设计一个算法：根据三人举手投票情况，判断某决定是否被通过。图1是使用Raptor软件制作的既可用于算法描述又可直接按流程执行的流程图。当学生们学习了分支结构的流程后，针对该任务所绘制出来的流程图有不少与图1类似。

不妨在头脑中想象一下投票的场景：如果您不是这三位投票者中的一位，那么您究竟是如何知道这项表决是否通过呢？如果投票人数非常多，或许就不得不去做加1计数的工作;然而，如果仅仅只有三位投票者，大部分人并不会真的去做加1的数学运算，而只是简单地看一下是否有两位或三位举手。这也说明，对于三人投票的场景，算法中的方法不一定如实地反映人头脑中的方法，之所以大部分学生在算法中用到了数学上的加法，是因为他们将普遍的涉及数字、符号以及相关数学运算的模型，很自然地应用到了这一特定场景中。

当人们提到“抽象”的时候，一般是指从一组事物中抽取共相的过程。那么，通过数学加法结合不等式判断来确定表决结果，与人头脑通过直观观察来确定表决结果，两者是否存在可抽取的共相？仅就三人投票的事件而言，如果共相存在，那应该只是存在于系统（将人的头脑和计算装置都视作系统）输入值和输出值的对应关系上，也就是说，就表决过程的外在效果而言，现实场景和模拟场景这两者的过程是一致的，但具体的内在判断过程却是不同的。对整个事件输入和输出过程的模拟，借助数学抽象和建模，完美模拟出系统表象上的功能，而流程图只是将用数学已经完成了的模型给描绘出来。那么问题是，学生将简单的数学模型运用在模拟表决过程中，这虽然可以说是数学思维的运用，但计算思维的运用又从何体现？

● 与计算思维相关的抽象与建模，和数学中的抽象与建模不同

接着考虑另一种情况，假设投票问题场景中的投票者人数有很大程度的增加，在现实中，这样的情况是难以用直观的方法来判断投票结果的。如果让一个没有学习过算法的学生来试着用流程图模拟此过程，很有可能会绘制出如图2所示的模样;或者，也会有学生绘制出一个类似循环结构的流程，但这个流程没有控制进出循环语句块的条件，而是直接标注有“问询所有人”的语句。虽然人的头脑很容易把握这些非标准的流程图的实质过程，但计算机并不具有直观地理解这些非标准的流程图中所要表达的“要向所有人搜集投票结果”这一意图的智慧。

从数学的角度看，“对集合中的所有元素进行某种一致的操作”是一个相当合理的要求。然而将这个要求转换为标准的流程图，却不得不增加许多细节。一个学习过算法的学生能比较像模像样地绘制出模拟投票场景的循环结构的标准流程图来，如使用某个变量来控制循环次数;使用诸如i=i+1这种通过将增加的值来覆盖变量自身值的方法来计数;在循环结构外对某个变量清零，在循环结构中用累加的方法统计投赞成票的数量。如果追问一下，这位学生是如何知道应当这样去做的，答案大概率是因为在学习时被告知要如此，或者是被软件（如Raptor）所限定而只能如此。

规范的流程图绘制方法有着相当统一的模式，但这种模式之所以是现在人们所看到的样子，其背后隐藏了模式形成的原因，而这个原因和机器实施计算的能力和方式是密切相关的。笔者认为，这些流程结构实际上是对机器底层的计算过程的封装和抽象，而并非是对某个现实事件的抽象。尽管可以将绘制流程图本身视作抽象和建模，但学生在学习用流程图描绘算法时，在将数学语言转化为规范的流程图时，只是运用了与计算思维有关的抽象和建模的已有成果，而并没有运用到计算思维本身;如果说学生们在问题解决过程中的确运用到了抽象与建模，那也仅仅是数学方法上的抽象和建模，其中不涉及计算机科学特有的方法。关于怎样的抽象和建模的过程运用到了计算思维，这个问题的答案恐怕非常复杂，可能涉及如何排除人脑的直观，更是涉及了关于可计算性问题的讨论。笔者考虑用一种简单的方法来判别计算思维运用与否的必要条件：解决问题的过程应当与日常头脑用数学方法直接进行计算并得出结果的过程是有所不同的。否则，便可以认为其运用了数学思维而非计算思维来解决了问题。

以上讨论是笔者设计下面这些流程图绘制任务的原因。任务是这样的：让学生们试着不用分支结构来完成原本需要用到分支结构的判断的功能。仍然以模拟三人投票为例，可行的方法不止一种，下页图3所示的是用序号加调用数组元素的方法，将总共8种投票情况按二进制方式计数，并转换为相应十进制数的索引，便能从数组中取出对应索引值的表决结果。而下页图4所示的是另一种方法，通过取整运算，将1设置为阈值，凡是大于等于1的情况，最后都显示1作为表决通过，小于1的情况，最后都显示0作为表决不通过，当然，同样可以借助数组的方法，将0和1作为索引值，调取文字显示的表决结果。在其他设计环境中，有更多的方法可以使用，如在Python中可以采用限定打印次数的方法，在逻辑电路中可以结合与门和或门形成组合逻辑的方法，等等。而不同的计算模型也有其各自颇具特色的方法，如用马尔可夫算法、标签系统、图灵机等都能够实现该任务，这里就不展开了。

本文接下来重点围绕图4所示的方法展开讨论，这种方法实际上揭示了一种可能性：在算法中，所谓的分支结构、循环结构都不是理所当然存在着的，在程序流程分支判断的时候，实际上是进行了某个运算，这个运算的结果就匹配了后续的某个动作。如果考察某个通用计算机底层的工作过程，就可以看出所谓的判断和分支，实际上是经历了对后续所要调用指令的地址的匹配过程。当学生们面对分支结构本身的时候，就已经是面对着一个现成的模型。虽然说基础教育阶段的学生一般不会学习到通用计算机底层实现相关的知识，但通过不用分支结构来完成原本需要用到分支结构的判断的任务，学生们能够直观地感知到，可以用数学的方法建立一个模型，来模拟出判断的过程，而不是直接用分支结构的语句来完成判断。这里必须区分“用分支结构完成数学判断”和“用数学方法完成分支结构的判断”两者的区别，后者的过程与日常头脑中用数学方法直接进行计算并得出结果的过程是不同的。如果用笔者提出的判别计算思维运用与否的必要条件，对于“用分支结构完成数学判断”这一过程是否运用了计算思维的结论是否定的，后者“用数学方法完成分支结构的判断”这一过程作为候选项存活了下来，但若说后者的过程确实运用到了计算思维，论据仍然是不充分的。

● 设计活动体现出为计算装置的能行而进行抽象和建模的过程

那么，何种情况下的抽象和建模，可以认为与计算思维的运用有关？对于这个问题，笔者遍查文献资料而未得，甚至很少有人将其作为问题来提出。笔者认为，是否考虑到一个计算装置的能行，是判断计算思维运用与否的一个充分条件。

关于三人投票表决的例子，除了通过对三人投赞成票总数除以2再取整的数学方法来实现模拟，还有另一种方法（大概是更接近现实的方法），即观察是否存在a和b同时举手，或a和c同时举手，或b和c同时举手，或a、b和c同时举手的任意一种情况。但因为a、b和c同时举手的情况已经包含了前三种情况，所以并不需要单独加以判断。如果写成逻辑运算式，就是r=a*b+a*c+b*c，其中所有变量都是布尔值的，若计算结果r为True，则当作表决通过，若计算结果r为False，则当作表决不通过。这样一来，算法流程也变得非常简单，只要输入三个投票数据（用1代表举手，0代表不舉手）后，计算并输出r值就可以了。

十分遗憾的是，或者说很幸运的是，Raptor这个流程图模拟软件只支持在判断框中进行逻辑运算，而不支持在处理语句框中进行逻辑运算。之所以说遗憾，是因为在教学中不得不放弃Raptor而改用其他工具来描绘通过逻辑运算模拟投票表决过程的算法。之所以说幸运，是因为Raptor软件能力的不足，恰恰提供了讨论计算装置“能行”问题的入口。

怎样让Raptor逻辑运算能力的“不可行”变为“能行”？考虑到Raptor中数学运算的能力是比较充分，所以可以试着用数学运算来模拟逻辑运算（计算机的真实运行过程恰恰反过来：用逻辑运算模拟数学运算，而计算机自身的逻辑运算是依靠硬件电路实现的）。可以发现，逻辑的与运算可以简单地用乘法来模拟，但逻辑的或运算却不能简单地用数学中的加法来替代。因此，希望能创设某个数学公式，当两个输入均为0的时候运算结果也为0，当两个输入有一个1，或两个都是1的时候，运算结果都为1。

有没有这样的公式呢？人工智能中的感知器概念提供了解决思路，那就是为输入值设置权重和偏置。在Raptor软件中可使用以下公式：

r=floor（a*0.8+b*0.8+0.2）

当a和b变量的输入值限定为0或1的时候，计算r值的过程就模拟了逻辑或门的运算过程。在该公式中，0.8是权重，而0.2是偏置。如果在Python环境中，使用公式r=int（a*0.8+b*0.8+0.2） 也能实现同样的效果。虽然说Python具备了完整的逻辑运算功能，并不需要用这样的办法来进行模拟，但也可以在教学中故意限制逻辑运算符的使用，让学生思考如何找到替代逻辑运算的方法。

当前，计算机底层的逻辑运算是依靠晶体管或场效应管来实现的，但人的头脑中神经元的运作方式，相对而言却与设置权重和偏置的方法更为接近。这让人联想到在关于计算思维内涵的讨论中，认为计算思维包含了运用计算机科学的基础概念对人类行为进行理解的思维活动的观点。

根据用数学方法模拟出的或门，再结合用乘法模拟的与门，可以将Raptor的流程图描绘成图5所示的样子。

该算法首先通过某种特定的数学计算来模拟逻辑门的功能，使得数学模型的输入和输出与逻辑运算的输入和输出具有一致性，然后再利用模型的功能来实现更高层次上的功能。这就体现出了为计算装置的能行而进行抽象和建模的过程。