基于J-C 模型的11MnNiMo 钢本构参数标定及验证

何沐阳，韦家祥，尹佳静，隆霞，周琛

哈尔滨工程大学 航天与建筑工程学院，黑龙江 哈尔滨 150001

由于动态载荷的瞬态特性，动态断裂与准静态断裂有很大的不同[1-4]。自20 世纪70 年代以来，材料动态断裂力学与相关的断裂问题逐渐被学者关注。在金属材料受到冲击、爆炸、碰撞等高速撞击载荷作用时，应变速率达到102～104s-1，此时金属材料会产生巨大的塑性变形。在高应变率加载下，材料的力学性能呈现明显的率相关性。针对冲击载荷，材料瞬态响应的本构模型常见的有Johnson-Cook(J-C)模型[5]、Steinberg 模型[6]和Zerilli-Armstrong 模型[7]等。

在高应变率下延性金属材料的断裂模拟中，由于J-C 模型各项物理意义明确，且相对容易获得，得到了广泛的应用。Gambirasio 等[8]评估了5 种可用于校准J-C 强度模型参数的方法。Banerjee等[9]通过实验确定了典型装甲钢材料的J-C 模型的模型参数，利用实测参数模拟了装甲钢试件的冲击试验，得到了可靠的结果。文献[10-11]基于J-C 模型分别成功地实现了马氏体时效钢300 和6061 铝合金的夏比冲击试验建模与仿真。

本文通过试验方法研究了支承结构常用的11MnNiMo 钢在不同加载条件下的性能，通过试件的准静态单轴拉伸试验和霍普金森压杆试验确定了J-C 本构关系的模型参数，最后通过夏比冲击实验和有限元模拟对比验证了参数的准确性，为支承结构材料的动态断裂分析和安全设计提供了参考。

1 J-C 参数标定

MnNiMo 合金钢广泛应用于压力容器及其支承结构等关键部位，本实验选用11MnNiMo 钢对支承结构断裂性能进行探究，所涉及材料均由同一钢板制备而成。

1.1 准静态材料拉伸实验

本实验依据《金属材料 拉伸实验 第1 部分：室温实验方法》[12]标准进行测试。

试件尺寸如图1 所示，为保证准确性，每组实验重复3 次。实验仪器采用INSTRON-5500R 万能实验机，设置加载速率为2.4 mm/min，应变率为0.001 s-1。

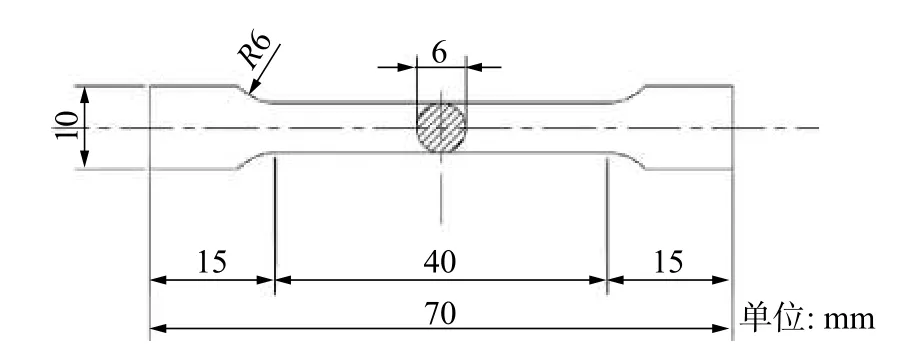
图1 拉伸试件尺寸示意

根据实验得到常温下11MnNiMo 钢的工程应力-应变曲线如图2 所示。

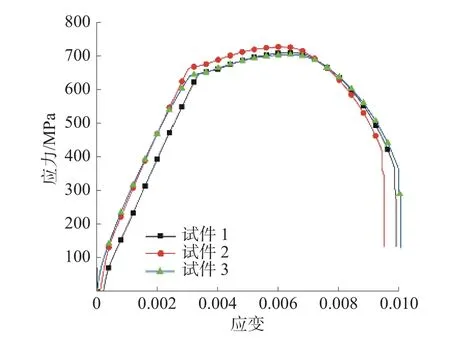
图2 11MnNiMo 钢拉伸应力-应变曲线

结合材料的出厂报告，整理得到11MnNiMo钢的各项材料力学性能：密度ρ为8 144 kg/m3，弹性模量为195 GPa，泊松比为0.28，屈服强度为644 MPa，极限强度为728 MPa，伸长率为20%。

1.2 霍普金森压缩实验

压缩试样选取截面为7 mm×7 mm 正方形、高为3.5 mm 的长方体试件。所测试的应变率分别为486、1 012、1 456 s-1，相对应的测试试件编号分别为D1、D2、D3、E1、E2、E3、F1、F2 和F3，如图3 所示。

图3 霍普金森压缩实验试件

霍普金森压杆实验中导杆参数如表1 所示，实验装置如图4 所示。在入射杆和投射杆上分别粘贴一个应变计用于采集波导杆上应变情况，入射杆上应变计与试样端部的距离为a1=1 200 mm，透射杆上应变计与试样端部的距离为a2=600mm。动态应变仪应变标定值1V对应500×10-6应变，采样间隔时间为0.8 μs。

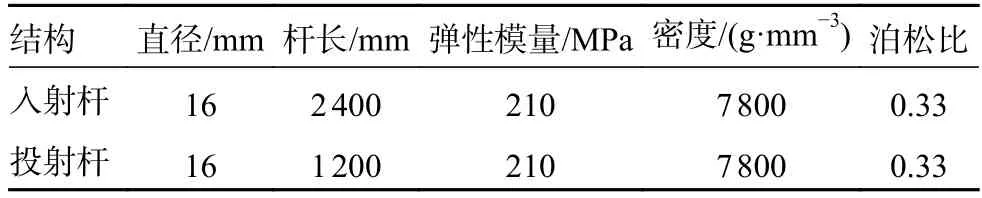
表1 霍普金森杆结构尺寸与材料性能

图4 霍普金森实验装置

实验中通过改变撞击子弹的长度实现输入载荷的调整。同时每次实验结束后应记录间隔测速仪的时间读数，计算撞击速度。实验数据如表2所示。

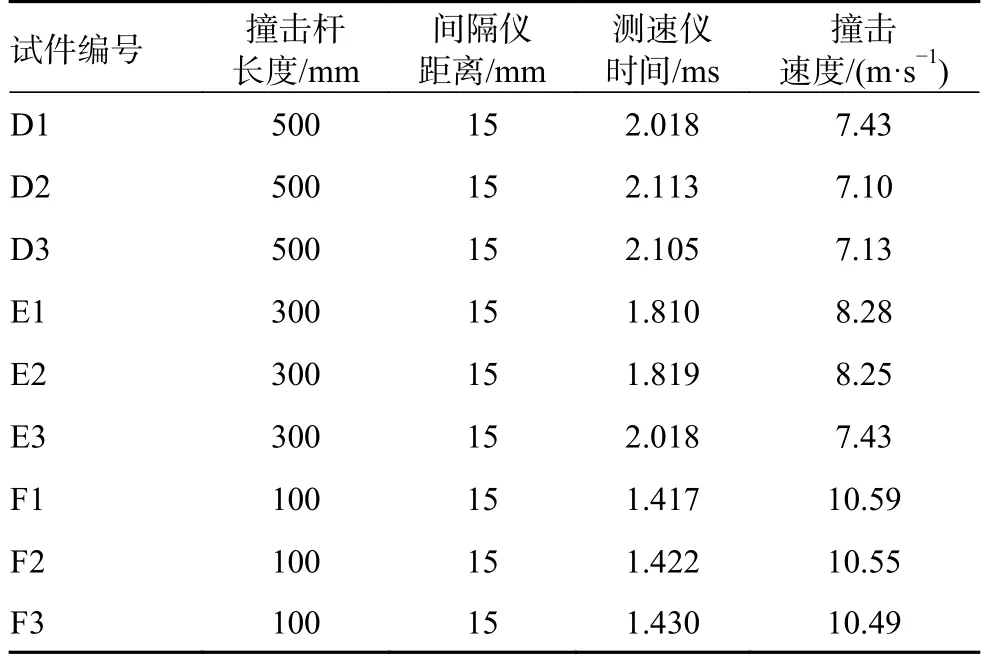
表2 实验数据记录表

为使实验过程中试件可以保持在恒定应变率，应选用塑性较好的材料置于入射杆与子弹撞击的一端，以便对波形进行一定程度的整形优化。

由于霍普金森实验的数据曲线震荡明显，为便于计算应对曲线进行平滑处理，通过霍普金森压缩实验获得常温下486、1 012、1 456 s-1这3 种不同应变率情况工程应力-应变曲线，如图5 所示。

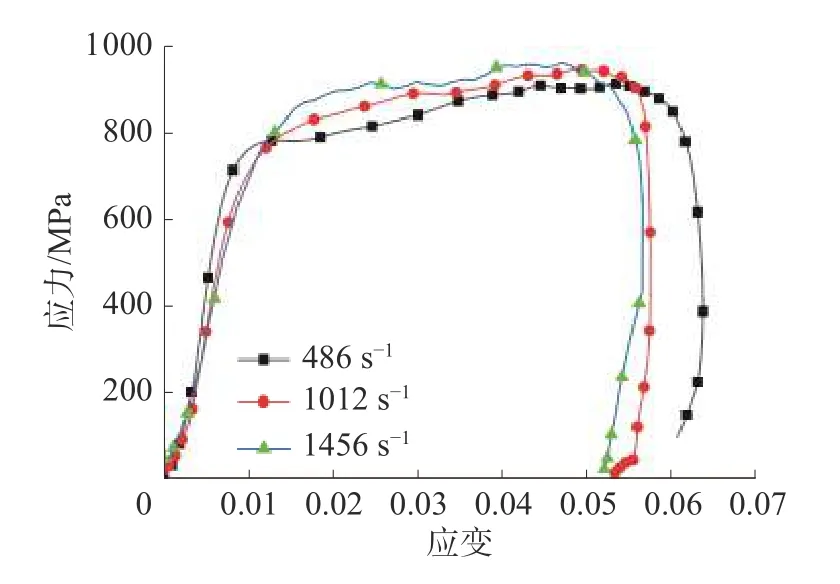
图5 不同速率下11MnNiMo 钢的压缩应力-应变曲线

1.3 J-C 模型参数计算

上述拉伸实验与霍普金森压缩实验所获得的工程应力-应变曲线并没有考虑到拉伸过程中截面会随长度增加不断缩小，试件受力面积时刻发生变化。在对J-C 表达推导中应使用材料的真实应力-应变曲线，即对瞬时的截面面积与长度进行求解。假设材料体积不变，真实应力为

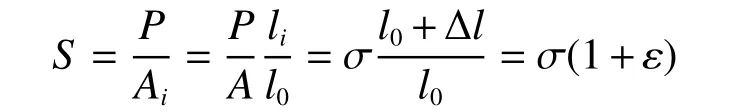
式中：S为真应力，l0为试件原始长度，li为瞬时长度，P为外载荷，A为原始面积，Ai为瞬时面积，σ为工程应力，ε为工程应变。

真实应变为

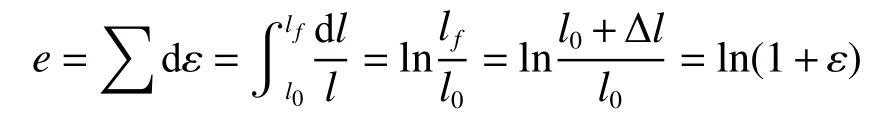
式中：e为真应变，dl为长度微增量，lf为最终变形长度。

通过工程应力应变转换得到的准静态拉伸与霍普金森压缩的真实应力-应变曲线分别如图6和图7 所示。

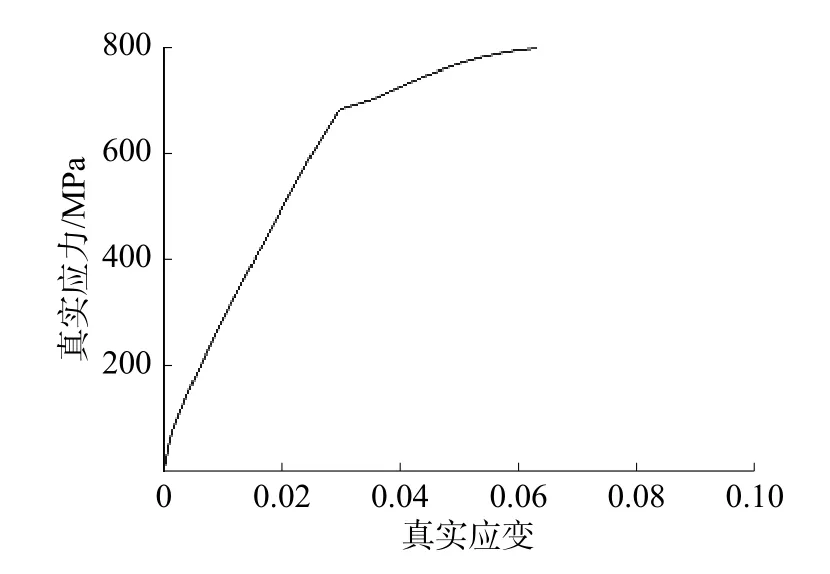
图6 准静态真实应力-应变曲线

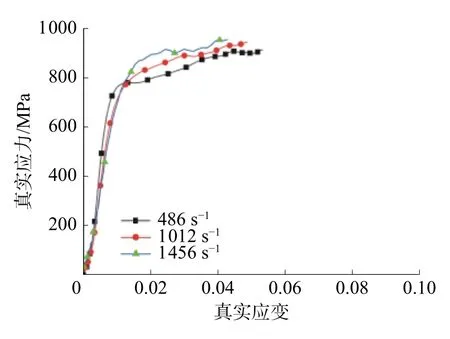
图7 霍普金森压缩实验的真实应力-应变曲线

由图7可以明显看到，11MnNiMo钢在应变率为1 456s-1时，动态屈服应力为原来的1.16倍。在高应变速率下材料出现一定程度的应力强化效应。由准静态拉伸实验与霍普金森压缩实验得到的不同应变率下的应力应变曲线，可以根据逐步估计法确定J-C 模型参数，即将硬化效应与应变率效应解耦，分为2 步进行参数求解。

1)通过准静态拉伸实验估计参数a、b和n。

式中a为准静态屈服强度，其大小为644 MPa。

对式(1)进行转换：

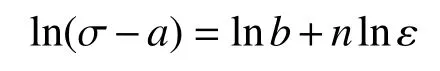
由真应力-应变曲线，将应变减去屈服前的弹性应变得到真实应力-塑性应变关系，利用最小二乘法进行拟合，可推出：n=0.64，b=1391 MPa。

2)通过霍普金森压缩实验确定参数C。

选取应变为0.04 时对应的各应变率下的应力值，采用式(2)进行拟合。

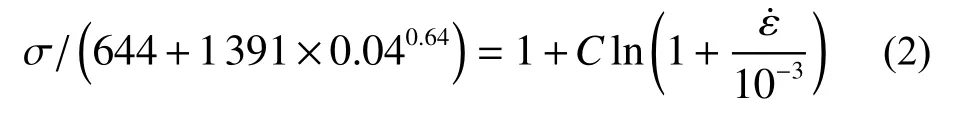
综上可以确定，11MnNiMo 钢忽略温度项的J-C 本构模型为

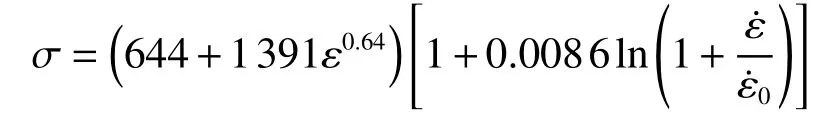
式中参考应变率

2 J-C 参数验证

2.1 夏比冲击实验

本实验依据《金属材料 夏比摆锤冲击实验方法》[13]标准进行测试。

夏比V 型缺口试件(Charpy V-Notched)尺寸为：长度l=55 mm，高度h=10 mm，宽度w=10 mm；在长方体中间预制2.0 mm 的V 型缺口。为确保动态断裂实验的准确性，共选取5 个试样进行实验，编号为1—5。试件尺寸示意图与测试试件分别如图8 和图9 所示。

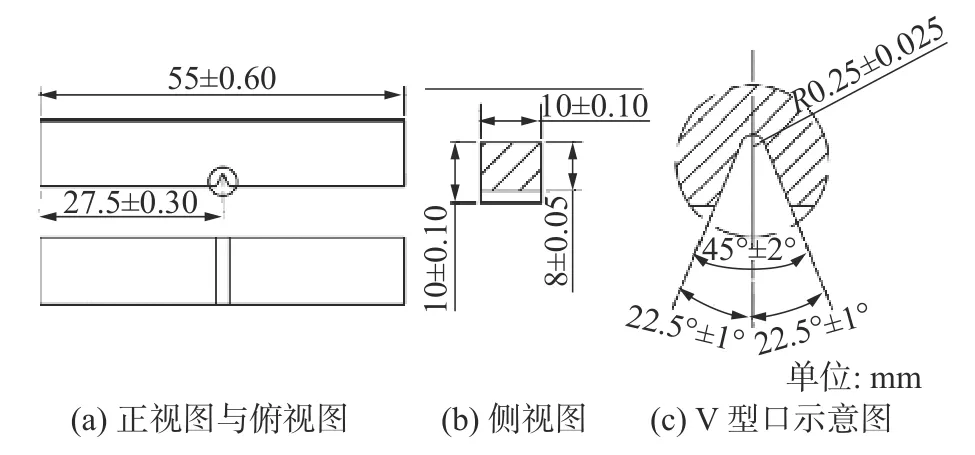
图8 夏比冲击试件尺寸示意

图9 冲击前后试件照片

本实验使用的摆锤实验机最大冲击能量为300 J，最大冲击速度为5.23 m/s。整理数据后发现4 号试件实验结果与其他相差较大，这是由于实验过程种试件摆放位置有偏差，因此本研究仅列出4 个较统一的试件结果进行分析。11MiNiMo钢夏比冲击试件的载荷-位移示波曲线如图10 所示。

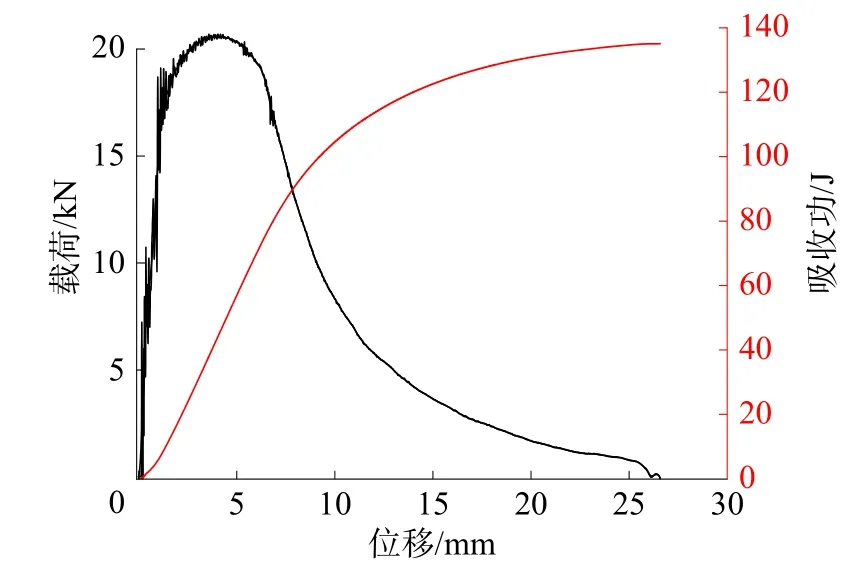
图10 夏比试件实验示波曲线图(1 号试件)

夏比冲击特征值实验数据如表3 所示。

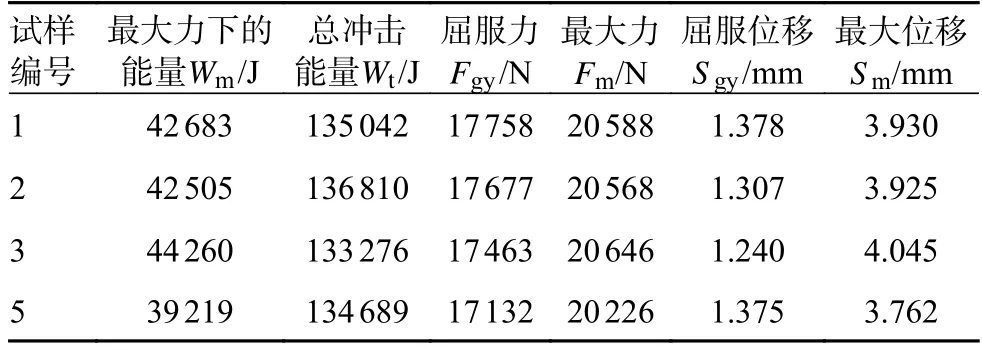
表3 11MnNiMo 夏比冲击特征值实验数据

夏比冲击实验通常是为了获得材料在动态冲击下的断裂韧性。对于动态断裂韧性的计算，最为重要的便是起裂时间的确定。本研究利用柔度法[14]确定试件的起裂时间。

柔度法表达式为

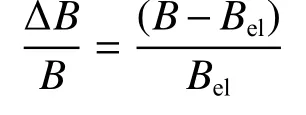
式中：B=Δd/ΔP为割线柔度；Bel为切线柔度，Bel=d/P；d为当前点位移；P为载荷。

当试件开始起裂时，ΔB/B的斜率会发生改变，此拐点可以认为是起裂点。采用柔度变化率法对本实验进行处理，得到曲线如图11 所示，柔度变化率的拐点发生在3.55 mm 位移处，由曲线积分至该点，此时的吸收功为38 023 mJ。根据实验结果，柔度拐点处载荷为20 444 N，可知在最大载荷处之前已形成裂纹。根据柔度变化率法对应的裂纹形成处，该点力占最大力值的99%，该点能量值占最大力点能量值的89%，与文献[15]中的结论一致。由柔度法测得的起裂时间为0.69 ms。

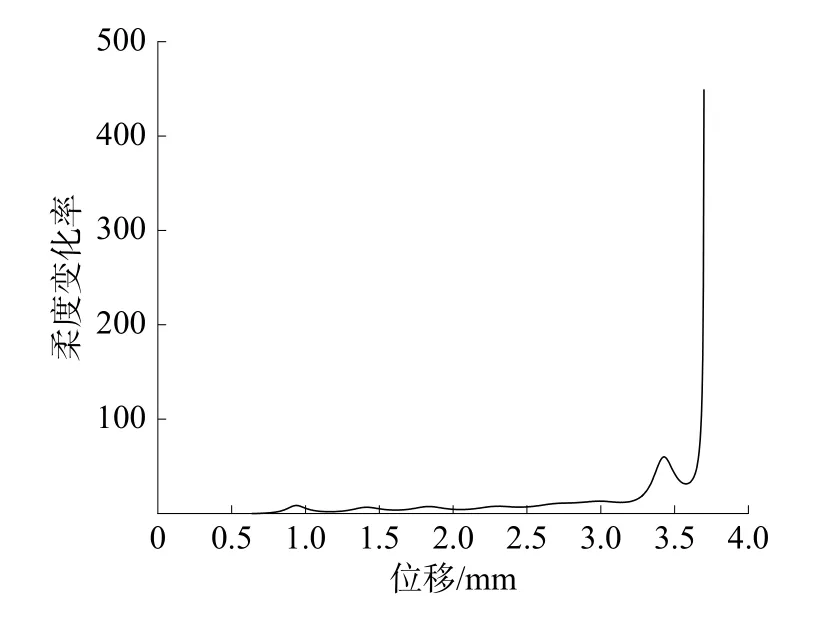
图11 柔度变化率曲线

2.2 有限元模拟

在ABAQUS 软件中建立夏比冲击有限元模型，如图12 所示。材料参数与实验获得相关参数一致。分析步长设置为8 ms，分析类型为显式动力分析。锤头非加载方向位移为0 mm，锤头转角为0°，在锤头打击方向设置预定义速度场5.23 m/s，左右两支座完全固支。定义各接触面为切向接触，考虑为接触约束，摩擦设置为罚函数，系数设为0.2[16]。

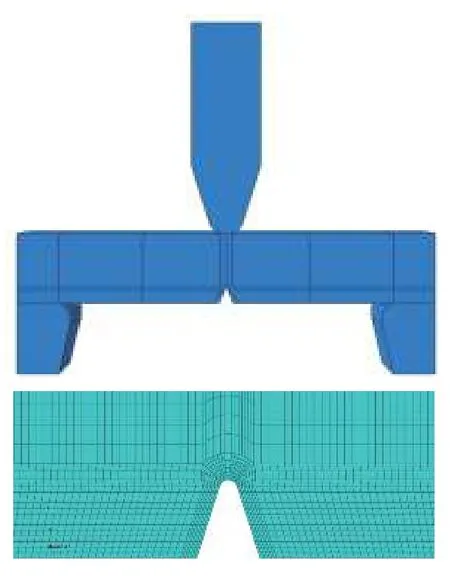
图12 夏比冲击有限元模型示意

实验获得的起裂时间为0.69 ms，此时刻锤头位移为3.55 mm。根据有限元模型的输出结果，提取0.69 ms 时的变形与应力云图，分别如图13和图14 所示。

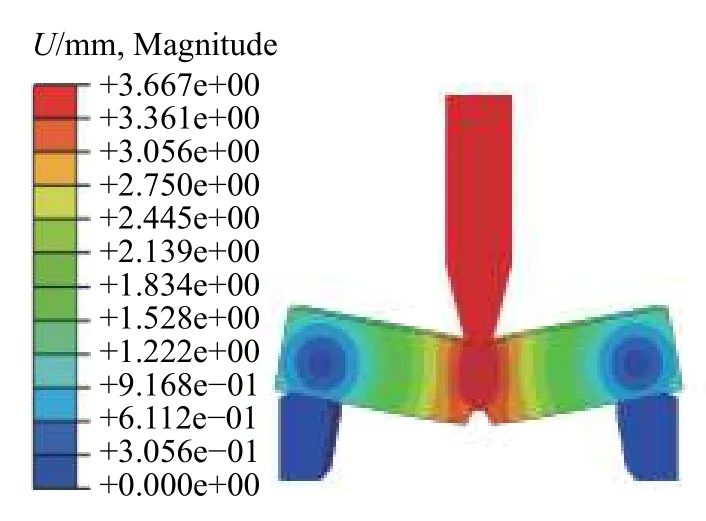
图13 夏比试件0.69 ms 时的变形云图

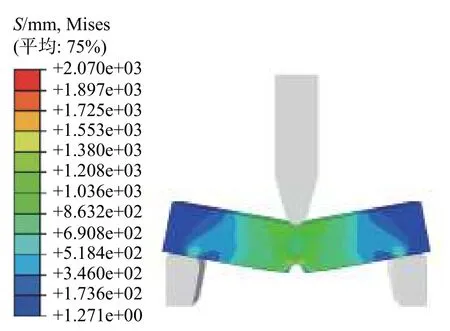
图14 夏比试件0.69 ms 时的应力云图

与实验结果进行对比可知，在裂纹起裂前，试件对锤头速度的影响不大，试件的裂尖最大位移与锤头位移一致，位移变形与实验情况相同。在0.69 ms 时锤头位移为3.667 mm，实验与有限元锤头位移结果的误差为3.3%，故在试件起裂前，有限元模型能够较好地模拟试件的变形状态。

3 结论

通过准静态单轴拉伸实验和霍普金森压杆实验确定了11MnNiMo 钢的Johnson-Cook 本构模型参数，并通过夏比冲击实验以及有限元模拟验证了实验测得的参数的准确性。具体结论如下：

1)通过准静态拉伸实验和霍普金森杆压缩实验确定了11MnNiMo 钢忽略温度项的J-C 本构参数：a=644 MPa，b=1 391 MPa，n=0.64，C=0.008 6。

2)夏比冲击实验中的起裂时间为0.69 ms，所对应的位移为3.55 mm。而有限元模拟过程中，0.69 ms 时所对应的位移为3.667 mm，误差为3.3%，证明了本文所测得的J-C 参数能够较准确地预测11MnNiMo 钢材的冲击特性。