Analysis of Cavity SGEMP of Cylindrical Cavity at Pulsed Power Facility
CHEN Jinghui, ZENG Chao,*, WANG Kunlun, ZHOU Kaiming
(1.Institute of Electronic Engineering, China Academy of Engineering Physics, Mianyang 621900, China; 2.Institute of Fluid Physics, China Academy of Engineering Physics, Mianyang 621900, China)
Abstract: Cavity system-generated electromagnetic pulses (cavity SGEMP) were experimentally studied by exposing a cylindrical cavity to the X-ray environment of a pulsed power facility at Institute of Fluid Physics, China Academy of Engineering Physics. The electric fields in the cylindrical cavity were measured using a netlike antenna, and a finite difference-time domain (FDTD) particle-in-cell (PIC) code was applied to simulate the cavity SGEMP in the cylindrical cavity. The gas in the enclosure could reduce the electric fields, which could be enhanced by increasing the dose rate.
Key words:cavity system-generated electromagnetic pulse; pulsed power facility; X-ray
1 Introduction
An X-ray environment enhanced by extreme conditions can produce system-generated electromagnetic pulses (SGEMP) in electronic systems or devices[1-5]. Photoelectrons knocked out by photons excite a high SGEMP electromagnetic field and may reach several MV/m close to the emission surface. As the high-fluence X-ray environment cannot be accessed, researchers have studied SGEMP via pulsed power facilities in laboratories.
In 1973, a dielectrical-filled cylindrical cavity exposed end-on to the Hermes Ⅱ by Brumley et al. to examine the SGEMP response, in this research, a dipole grid sensor was employed to acquire axial electric field[6], and William et al. researched the parametric data and develop criteria needed in the design of dipole grid sensor in 1974[7]. The scaling laws for the nonlinear SGEMP problem were explored through theory and experiments by Woods et al. in 1974[8]. In 1977, Murphy et al. developed a thin-film sensor to measure the space current of SGEMP in radiation environment[9]. From these researches, we can summarize the characteristics of cavity SGEMP: First, space charge limited effect exists at high dose rate; Second, the ionization of air will reduce the effect of space charge limited; Third, the ionization of air will turn the air into the lossy medium of electromagnetic wave, and reduce the electromagnetic field.
In this paper, the pulsed power facility of the Institute of Fluid Physics, one of the highest dose rate X-ray sources of China is applied to study the cavity SGEMP in a cylindrical cavity. The influences of air pressure and dose rate on cavity SGEMP are studied. In addition, by establishing the model of cavity SGEMP, this paper compares the results of calculations and measurements. The research in this paper is the first time to study cavity SGEMP at this pulsed power facility, and the experimental results with high signal-to-noise ratio at this high dose rate are obtained for the first time in China. Section 2 introduces the X-ray environment of the pulsed power facility, and the experimental configuration, test system of the experiments. Section 3 introduces the theory of cavity SGEMP. Section 4 introduces the experimental results and the predictions of calculations. Section 5 summarizes this article.
2 Experiment at pulsed power facility
The experimental investigation involved exposing an aluminum cylindrical cavity to the radiation pulse of the pulsed power facility.
2.1 X-ray environment of pulsed power facility
High-current electron beams driven by pulsed power can produce intense pulsed X-ray with appreciable efficiency. The pulsed power facility constructed at the Institute of Fluid Physics can produce intense pulsed X-ray by using a reflex triode, series diode, or ring diode. The photon energy is in the range of tens to hundreds of kilo-electron volts (keV) in the case of a reflex triode or series diode, or in the range of 100 keV-2 MeV in the case of a ring diode. Generally, the radiation area is over 400 cm2(2∶1), with a peak dose rate over 109Gy(Si)/s and a duration of 20-60 ns.

Fig.1 Energy spectrum of X-ray produced by reflex triode and diode
The energy spectrum of X-ray produced by the reflex triode and ring diode are shown in Fig.1, and the spatial distribution of photons was dominated by two terms. The first term was corresponded to the sight of view of the source. It contributed about 80% of the spatial distribution. The second term was corresponded to Compton scattering of photons by an X-ray window and nearby structures, which can be described by the Compton scattering equation:
(1)
whereI0is the radiant intensity produced by the source,R1is the distance between the source and a small volume,R2is the distance between the small volume and sampling point,neis the number of electrons,Iis the X-ray intensity,Vis the material volume,σis the X-ray diffraction cross section, andΩis the diffraction solid angle. A Monte Carlo code was applied to solve the equation, with randomly generated points as shown as in Fig.2. It involved those photons came from the source cone which was about 88% of the total, where the cone angle was about 32 degrees.
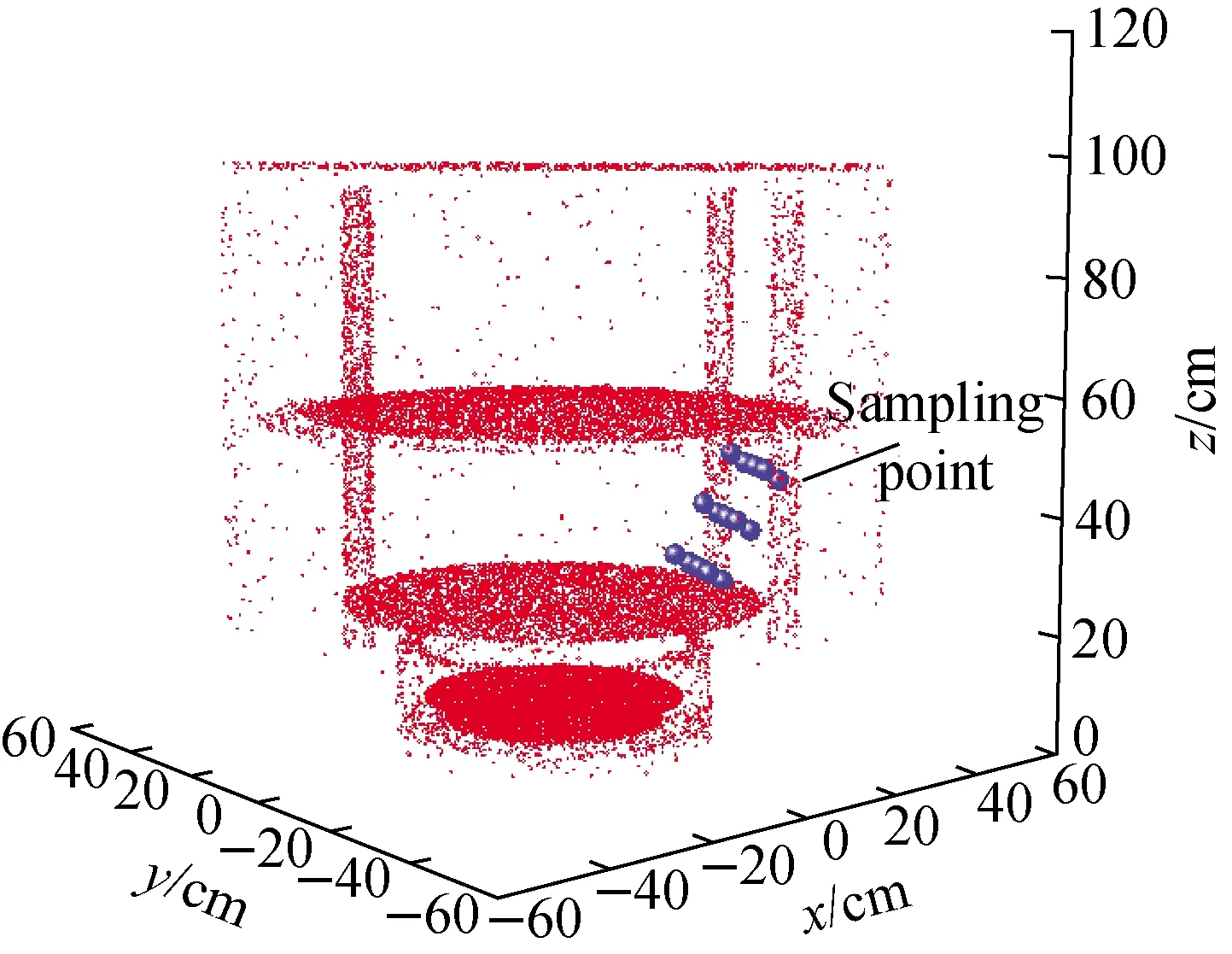
Fig.2 Spatial distribution of photon in pulsed power facility
2.2 Cavity construction
The cavity geometry is shown in Fig.3, the two end plates are made of 2 mm thick aluminum, and the side wall of the cavity is made of 1 mm thick aluminum.
2.3 Sensor
In order to measure the electric fields implicitly within the cavity, a dipole grid sensor was used to record an axial electric field related signal. The sensor consists of two 0.1 mm thick grids, and 1 mm space between these two grids, the grids are made of aluminum to reduce the electron yield of grids themselves. The two grids are connected to the inner conductors of two coaxial cables.

Fig.3 Experimental cavity geometry
The location of the sensor within the cavity is shown in Fig.4.

Fig.4 Location of dipole grid sensor within cavity
2.4 Experimental setup
The experimental setup is shown in Fig.5. The cavity was placed at a polymer board, and one side of the cavity was uplifted a little degree to make dose more uniform. Some TLDs were placed near the cavity to obtain the dose of X-ray. The electric signal was changed to optical signal through an electric-to-optical module to reduce the interrupt of EMP[10].
Three operation modes were applied to produce different X-ray environments, they were ring diode mode, ring diode mode with vacuum and reflex triode mode.
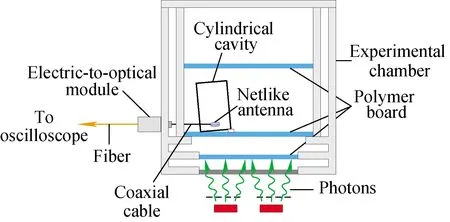
Fig.5 Schematic of experimental setup
3 Theoretical model
The theoretical model considered in this investigation has, in part, been reported previously[4]. The geometry is the same as it in experiment and is shown in Fig.3 and Fig.4. The characteristics of X-ray are simplified to reduce the difficulty of calculation, the spectra of X-ray are replaced by the central energy,and the doses of X-ray are replaced by the doses at the center of the end plate. A Monte Carlo program is applied to obtain the spectra of electron emitting from the end plate. The central energy of X-ray of ring diode mode and reflex triode mode is 500 keV and 100 keV respectively, and spectra of emitting electron of these two modes are shown in Fig.6. We simplify the spectra to discrete-spectra containing 10 energy points.
The method to calculate the cavity SGEMP is to solve the Maxwell equation and the Newton-Lorentz equation. So, we develop a finite difference-time domain (FDTD) particle-in-cell (PIC) code to simulate the cavity SGEMP in the cylindrical cavity.

a—Ring diode mode; b—Reflex triodeFig.6 Spectrum of emitting electron in different modes
4 Comparison between experiment and theory
The experimental results are shown and the theoretical predictions are applied to explain the characteristics or the laws of these waveforms in this section.
4.1 Ring diode mode
Two types of air pressure are tested in the ring diode mode, one is normal pressure, and the other is vacuum. The typical waveforms of these two cases are shown in Fig.7, and the X-ray parameters of these two cases are listed in Table 1. As the X-ray environments are similar for these two cases, the significant difference in the electric fields may be the result of air ionization in the cavity. This ionization occurred during the period of radiation, which resulted in the enhancement of air conductivity and led to the decline of electric fields.
Adding the model of air conductivity to cavity SGEMP theory can predict this phenomenon. Air conductivityσis defined as[11]:
σ=ρe(μeNe+μi(N++N-))
(2)
WhereNeis the number density of secondary electrons,N+andN-are the number densities of positive and negative ions respectively,μeandμiare the electron and ion mobilities respectively, andρeis the absolute value of electron charge.

a—Normal pressure; b—VacuumFig.7 Waveform of electric field in cylindrical cavity

Table 1 Parameter of X-ray of two cases
Considering a fixed position and for a constant air density, the equation representing the generation of conduction electron density is written as:
(3)
whereQis the electron source function,αeis the attachment rate of electrons to O2,Gis the electron avalanching of “breakdown” eff-ect rate, andtis the time.
With the calculation of the secondary electron density, only the electron mobility remains to be considered[11]. Thus, the air conductivity can be applied to the FDTD-PIC code to simulate electromagnetic fields under normal pressure. The waveforms of the electric fields are shown in Fig.8, where the red curves are the experimental results and the blue curves are the simulation results, which are approximately equal to the experimental results.
4.2 Reflex triode mode
A series of dose rates are set to study the influence of dose rate in the reflex triode mode. Two typical waveforms are shown in Fig.9, and the X-ray parameters of these two cases are listed in Table 2. The predictions of theory are also shown for comparison.

a—Normal pressure; b—VacuumFig.8 Waveform of electric field of calculation for different gas pressures
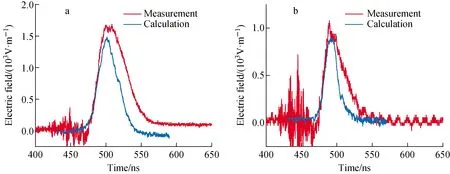
a—5.1×108 Gy(Si)/s;b—2.4×108 Gy(Si)/sFig.9 Comparison of measurement and calculation waveforms for different dose rates

Table 2 Parameter of X-ray of two cases
The calculation results are approximate to the experimental results, and the relative differences are shown in Table 3. The relative difference of half-width and peak value may be due to the simplification of calculation model. Furthermore, the Compton interactions on the two grids of sensor may also induce the error of measurement signals.

Table 3 Relative difference of measurement and calculation results
Although existing some relative differences between the experiment and calculation results, the theory gives relatively well predictions for the cavity SGEMP versus dose rate and the change of peak value versus dose rate are shown in Fig.10. The dose rates of these experiments are not high enough to produce obvious space charge limited effect, which lead to the linear change of peak value (The calculation results also prove this phenomenon).

Fig.10 Change of peak value versus dose rate
5 Conclusion
The X-ray environment produced by a pulsed power facility can generate cavity SGEMP in a cylindrical cavity. The parameters of X-ray, such as energy spectrum, dose rate and pulse width, can be changed using a reflex triode mode, series diode mode, or ring diode mode to study the influence of these parameters on cavity SGEMP.
From the results of experiments, the change in the gas pressure within the cavity could bring to the change of cavity SGEMP, and the theory of air conductivity could predict the phenomenon well. Those charged particles in cavity act as the lossy medium of electromagnetic wave, which attenuates the cavity SGEMP. The experiment results show that the peak values of electric field change linearly with dose rates when space charge limited effect is not significant.
The results of this article could provide help for studying the law of cavity SGEMP.
- 原子能科学技术的其它文章
- H-1NF仿星器标准磁场位形分析与高能量离子运动轨道模拟
- 铀转化生产线含氟废水处理工艺设计
- 在线进样ICP-MS用于239Pu气溶胶活度浓度连续监测技术研究
- Degradation Characteristic of Proton Irradiated 8T CMOS Image Sensor
- Comparative Experimental Study on Space Electrostatic Discharge Effect and Single Event Effect of 130 nm SOI D Flip-flop Chains
- Effects of Electron Irradiation at Different Energy and Fluences on Electrical Properties of InP HEMT Structure

