(2+1)维AKNS方程的初值扰动波及动力学行为

康晓蓉鲜大权鲜骊珠

(1. 西南科技大学理学院 四川绵阳 621010； 2. 成都理工大学中英合作办学 成都 610059)

1980年代由Ablowitz 等导出的如下形式的(2+1)维非线性演化模型[1]：

suxt+uxxxy+2suxyux+suyuxx=0,s∈R-{0}

(1)

被称为Ablowinz-Kaup-Newell-Segur方程(简称AKNS方程)。该模型描述了不同背景下的许多物理、化学现象，在一定条件下可约化为著名的Korteweg-De Vries方程、Sine-Gonden方程族和非线性薛定谔方程族等，科学内涵丰富，受到学术界广泛关注，诸多学者从不同方面对它展开了研究，近年来获得了一系列研究成果[2-10]。作为高维非线性模型，AKNS方程具有复杂的动力学特性，可用于研究AKNS方程的方法有很多[11-13]，本文应用初值扰动行波变换，结合相平面分析和椭圆函数展开法，探索(2+1)维AKNS方程的精确解在初始解扰动下的动力学行为特征及其局域激发结构。

1 方程初值扰动行波约化

取方程初值扰动波变换：

u=v(ξ)+a1x+a2y+a3(t),ξ=kx+ly-ct

(2)

其中a1x+a2y+a3(t)为方程(1)的一个初始解,a1，a2∈R,a3(t)为t的任意函数，k,l,c为非零行波参数。

将变换(2)代入方程(1)，对ξ积分一次取积分常数为B，得如下非线性常微分方程：

(3)

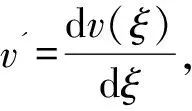
v'=w=w(ξ)

(4)

则有：

(5)

令2a1l+a2k-c=μ,方程(5)化简为如下形式：

2sμw+2k2lw"+3sklw2-B=0

(6)

(7)

取积分常数B=0，则动力系统(7)的两个平衡点为：

在平衡点处，系统(7)的Jacobi矩阵为：

其特征根分别为：

当sμl<0时,λ1为两不等实根,λ2为两共轭纯虚根；当sμl>0时,λ1为两共轭纯虚根,λ2为两不等实根。因此，系统(7)两平衡点或为中心点或为鞍点,故存在闭轨、同宿轨和异宿轨。

2 方程(6)的闭轨及同异宿轨解析表达

依潘勒卫分析思想[14]，对方程(6)作如下的椭圆正弦函数展开：

w=b0+b1SN+b2SN2

(8)

其中b0,b1,b2为待定常数，SN=SN(λξ,m)是模为m的Jacobi椭圆正弦函数，m∈[0,1]。

将(8)式代入方程(6)，得关于SN的四次多项式，取各项系数为零，得待定参数满足的非线性超定代数方程组如下：

(9)

当b1=0，m≠0,B=0,s,k,l,λ,μ,m满足关系

16k4l2λ4(m4-m2+1)=s2μ2

(10)

方程组(9)有唯一精确解：

因此得到方程(6)的Jacobi椭圆正、余弦波解及其初值扰动结构如以下3种情况：

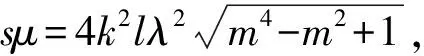
应用关系SN2(λξ,m)+CN2(λξ,m)=1,得：

其中CN(λξ,m)是模为m的Jacobi椭圆余弦函数，m∈(0,1]。当m≠1时，w1(ξ)和w2(ξ)均为闭轨。

(2)当ksλ≠0,m→1时,sμ=4k2lλ2,SN(λξ,m)→tanh(λξ),CN(λξ,m)→sech(λξ),则有:

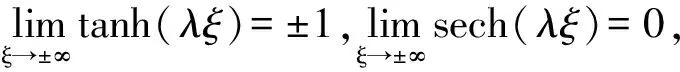
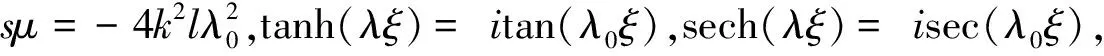
w5(ξ)和w6(ξ)均为闭轨。

3 方程(3)的精确行波解结构

将w1(ξ)-w6(ξ)式代入变换(4),取积分常数为零，则得方程(3)相应的扰动波精确结构如下:

以上结果v1(ξ)-v6(ξ)的结构包含两个扰动特征,v1(ξ)，v2(ξ)，v5(ξ)和v6(ξ)或为周期波，或为准周期波；v3(ξ)，v4(ξ)或为扭结波，或为准扭结波。

4 AKNS方程(1)的初值扰动波分析

4.1 方程(1)的行波初值扰动结构

将v1(ξ)-v6(ξ)代入式(2)得方程(1)的行波初值扰动解析结构分别如下：

(11)

(12)

(13)

(14)

(15)

(16)

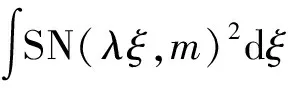
4.2 方程(1)的行波解初值扰动动力学特征分析

限于篇幅，仅以(14)式u4为例对方程的初值扰动动力学特征进行分析。

因为当m=1时，约束关系(10)化为4k2lλ2=sμ，将μ=2a1l+a2k-c代入可得到4k2lλ2=s(2a1l+a2k-c)，取l=s，则有：c=2a1s+a2k-4k2λ2。

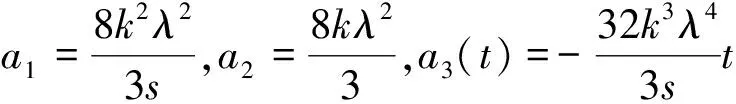
(17)

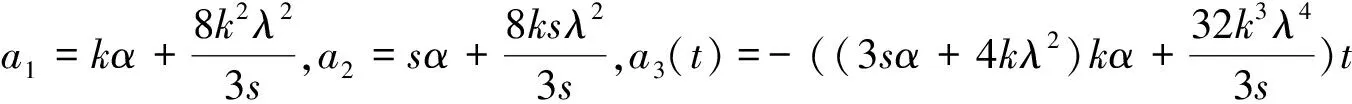
(18)

其中α为非零实数。特别地，当α=0时，u4b退化为扭结波解u4a。

(3)当(3sa1-3ksα-8k2λ2)(3sa2-3s2α-8ksλ2)(3sa3(t)+(3s(3sα+4kλ2)kα-32k3λ4)t)≠0时，得到广义初值扰动波解：

(19)

其中α为任意实数。

同理，上述u1，u2，u5和u6在初值扰动下的演化特征分别为周期波、准周期波与广义非周期波；u3在初值扰动下的演化特征分别为扭结波、准扭结波和广义非扭结波。

4.3 方程(1)的行波初值扰动解局域结构

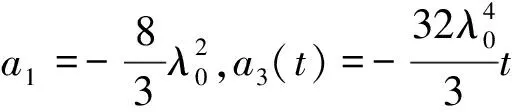
(20)

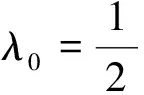
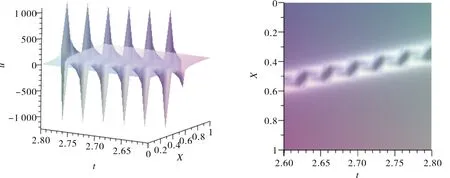
图1 u5a 的结构及投影Fig.1 Structure and projection of u5a

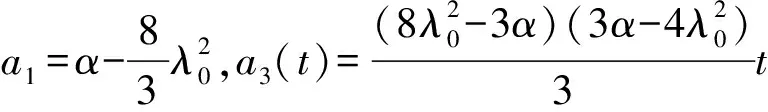
(21)

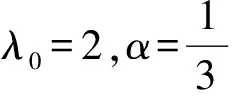
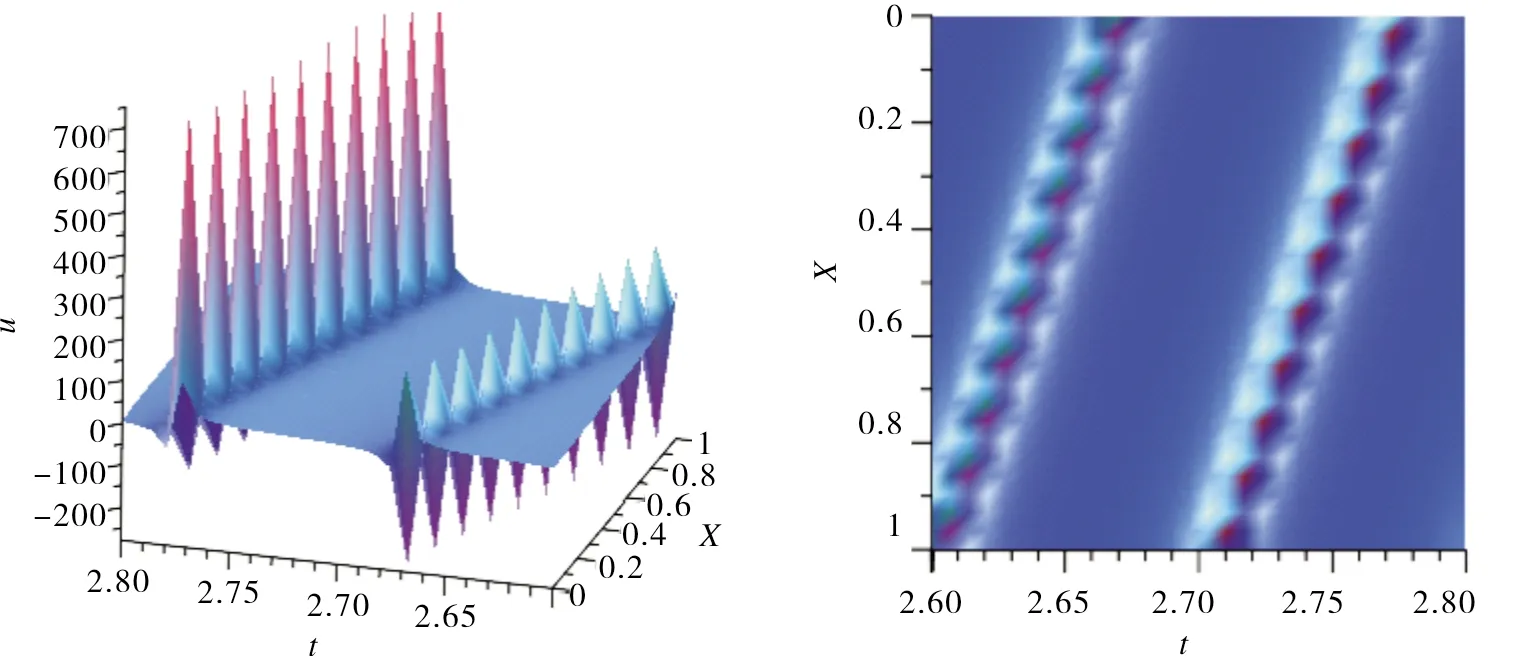
图2 u5b 的结构及投影Fig.2 Structure and projection of u5b

(22)

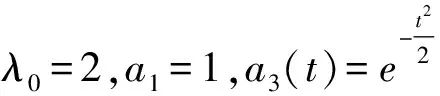
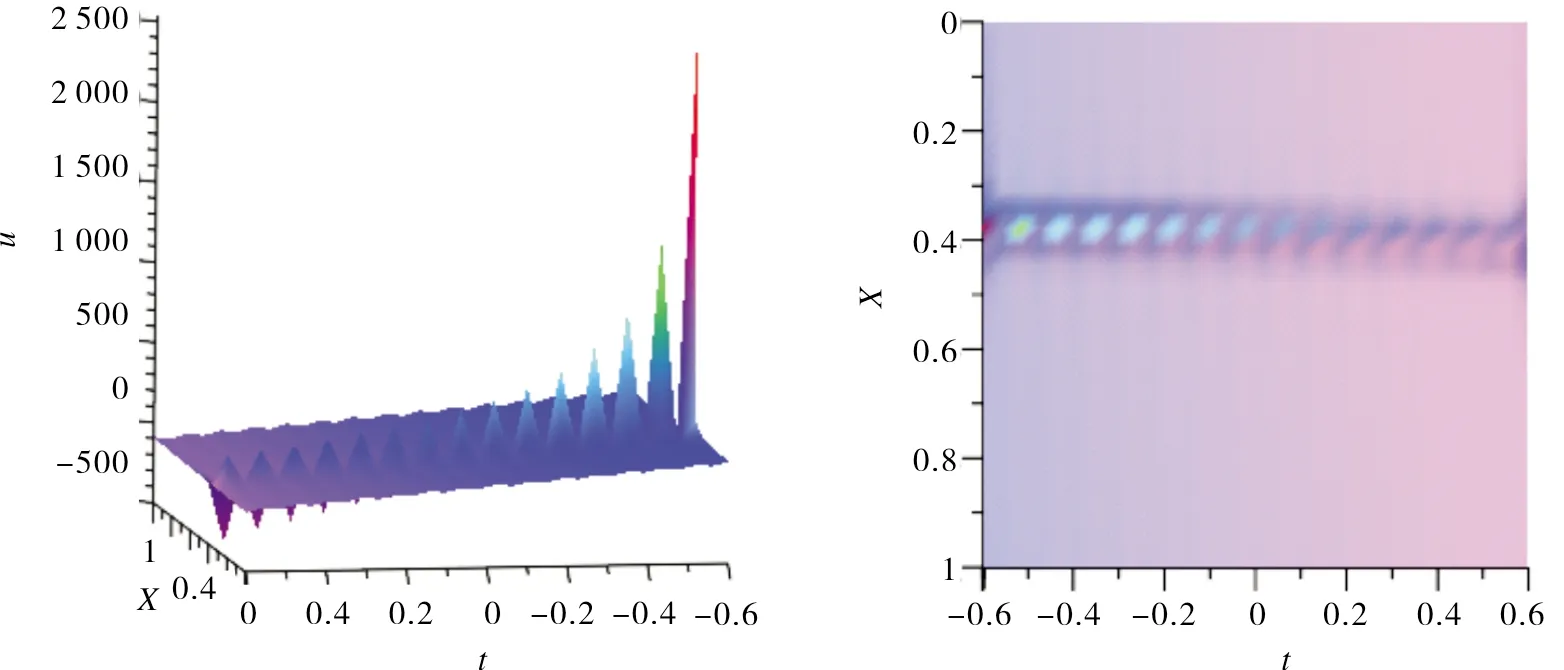
图3 u5c的结构及投影Fig.3 Structure and projection of u5c

5 结论

利用相平面分析法定性讨论了(2+1)维AKNS方程的行波闭轨和同异宿轨存在性，应用初值扰动行波变换和椭圆正弦函数展开法获得了方程的带时间任意函数初始解扰动的扭结波和周期波精确解结构。分析了方程的行波在初值扰动下呈现的三类特征，讨论了初值扰动精确解的局域几何结构。 本文所用的综合性研究思路和所获结果，既拓展了AKNS方程的研究方法，也进一步丰富了该方程的动力学内涵。