基于调节算子的多目标人工蜂群算法

赵新秋, 段思雨, 马学敏

(燕山大学,河北秦皇岛 066004)

1 引 言

随着工业生产能力的进步以及科学工艺的发展,在优化此类问题中往往需要多目标优化算法对多个冲突的目标同时进行优化,来获得一组权衡的解集.目前,多目标进化算法(MOEAs)[1−4]相继提出去解决复杂的非线性多目标优化问题,现已应用于参数优化[5−8]、车间调度[9]和数据挖掘[10,11]等领域,并取得了良好的效果.

人工蜂群算法(artificial bee colony algorithm)是一种仿生学群智能算法,该算法通过模拟蜜蜂采蜜的一系列过程,来解决现实中的复杂优化问题[12,13].由于其结构简单、易于实现且拥有较快的收敛速度,最初广泛应用于数值优化问题.目前,国内外学者对人工蜂群算法的改进主要包括加快算法收敛速度以及提高算法的多样性和分布性.

1)提高算法多样性和分布性.

单娴等[14]通过种群个体在搜索过程中自适应选择最佳搜索方式,提出一种复数编码的多策略人工蜂群算法,改善了种群的多样性;Akay[15]利用支配关系和非支配排序方法提出S-MOABC算法,结果表明算法能够获得一组分布性良好的解集;Yi 等[16]利用多重模型和动态信息交换策略,提出了一种动态多群体多目标人工蜂群算法.在此基础上提出一种基于分解的人工蜂群算法[17],将分解的思想引入蜂群算法中,对比其他算法能够取得一组分布性更好的解集;Luo 等[18]提出了一种基于评价指标的多目标人工蜂群算法,利用支配关系和偏好信息将每一代产生的非支配解加入到外部档案,在处理复杂多目标问题时可以保证良好的分布性;Zhang 等[19]提出一种基于多种群和区间可信度的多目标优化方法,在外部档案中利用精英学习策略,获得一组分布性优越的解集;Beheshti[20]将二进制编码方式引入算法,提出一种二进制邻域蜂群算法,改善算法的开发能力.

2)加快算法收敛速度.

Gao 等[21]根据差分进化算法的启发,通过混沌算子和反向学习方法对种群初始化,使用两种不同的搜索方式来解决但目标问题,提出IABC 算法;Akbari 等[22]提出的多目标蜂群算法,具有里程碑的意义,该算法采用自适应网格的方法对外部档案进行维护, 并利用精英蜂引导种群进化, 加快算法收敛速度; Xiang等[23]引入一种新的搜索方式,加入参数扰动平衡算法搜索和开发能力的同时,加快了算法的收敛速度;Liu等[24]将knee points 的概念引入蜂群算法,提高收敛速度的同时,保持了良好的分布性.

基于以上分析,本文提出了一种基于调节算子的多目标人工蜂群算法(multi-objective artificial bee colony algorithm based on regulation operators,RMOABC).为了改善算法开发能力弱的问题,在引领蜂阶段,根据蜜源动态的调节进化方向,平衡了算法的局部搜索和全局搜索能力;在跟随蜂阶段,提出了一种根据种群分布的概率计算方式,合理利用多样性个体对种群进行更新;在外部档案维护阶段,算法将外部档案中的解进行维度融合,保证外部档案的多样性,并将其作为最后的输出结果.通过与其他4种算法在基准测试函数进行仿真比较,验证了本文算法的在收敛速度以及分布性上有一定提升.

2 标准人工蜂群算法

人工蜂群(artificial of bee colony,ABC)算法是一种新兴的群体智能模型,是通过模拟自然界中蜂群寻找蜜源过程的仿生智能算法.在整个过程中,每个蜜源代表寻优过程中的可行解,并且根据不同的分工,蜂群被分为三类: 引领蜂(employed foragers)、跟随蜂(onlookers)和侦查蜂(scouts).三类蜜蜂在整个过程中,相互分享信息,促进整个群体进化,完成整个寻优的过程.

使用ABC 算法求解问题时,首先,需要对种群进行初始化操作

其次,对引领蜂位置进行更新进化

其中k=1,2,...,N/2 且,j=1,2,...,D,rij ∈(−1,+1),vij为新产生的候选解的第j维分量.

在整个搜索过程中,跟随蜂通过引领蜂分享的信息,根据蜜源质量使用轮盘赌策略选择一个合适的蜜源进行开采,蜜源选择概率为pi=其中Fi为适应度值.

以最小化问题为例

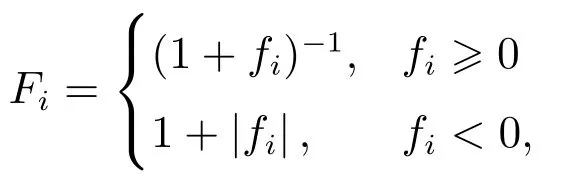
其中fi为第i个解的优化目标函数值.

选择优异的蜜源后,跟随蜂按照式(2)对蜜源进行深度开发.在引领蜂和跟随蜂完成更新过程后,通过对适应度进行贪婪选择,确定是否保留新产生的解.最后,若某个个体循环更新次数达到阈值(Limit),其解的质量还没有得到改善,则放弃该蜜源,引领蜂转化为侦查蜂,按照式(1)对蜜源进行重新初始化,产生一个新个体替代原有个体.

3 基于调节算子的多目标人工蜂群算法

3.1 基于个体阈值的更新公式

标准人工蜂群算法存在精于搜索,疏于开发的问题.在通过ABC 算法求解多目标优化问题时,由于同时存在多个互不支配的解,种群中个体通过信息交流搜索新蜜源,整个过程随机性大,ABC 算法虽然具有较强的全局搜索能力,但并没有通过充足的开发来找到一组最优解,算法局部搜索能力较差,当逐步接近Pareto前沿时开发效率明显降低,导致算法整体搜索能力强开发能力弱.在蜜源开发末期,如果继续使用式(2)对蜜源进行开发,蜜源质量基本得不到改善,整体多样性缺失.在搜索过程中,为了进一步控制搜索进度,以平衡人工蜂群算法中全局“搜索”和局部“开发”的能力,引入了两种调节算子: 局部调节算子和全局调节算子.针对蜂群算法在进化前期,在精英个体的引导下易陷入局部最优,通过加强当前食物源与邻域内食物源进行信息交流共享,提高算法的寻优特性.针对人工蜂群算法收敛速度慢的缺陷,通过在进化中期加强精英解对种群的引导作用,使种群能够快速收敛到近似Pareto 前沿.在进化后期,为避免丢失种群多样性,通过与邻域内个体充分交流,以保证在收敛到Pareto 前沿时具有良好的分布性.将引领蜂阶段新的位置进行更新,即

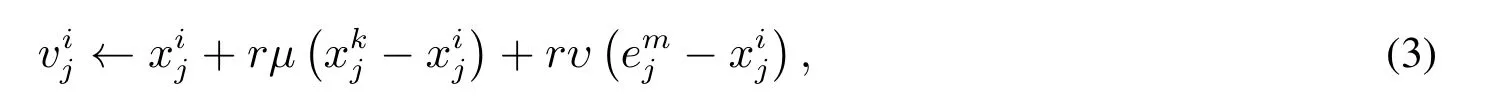
其中k= 1,2,...,N/2 且k=i,j= 1,2,...,D,µ ∈[−Φ,+Φ],υ ∈[−Ψ,+Ψ],Ψ= sin(πti/Limit),Φ=|cos(πti/Limit)|,r ∈[1,1.75](通过设计重复性实验确定最优取值范围,由于篇幅所限,没有列出详细的实验过程),e是外部档案中随机选择的一个解,ti是蜜源i当前开发的阈值,Limit 是蜜源开采最大阈值.

调节算子和阈值曲线如图1 所示.

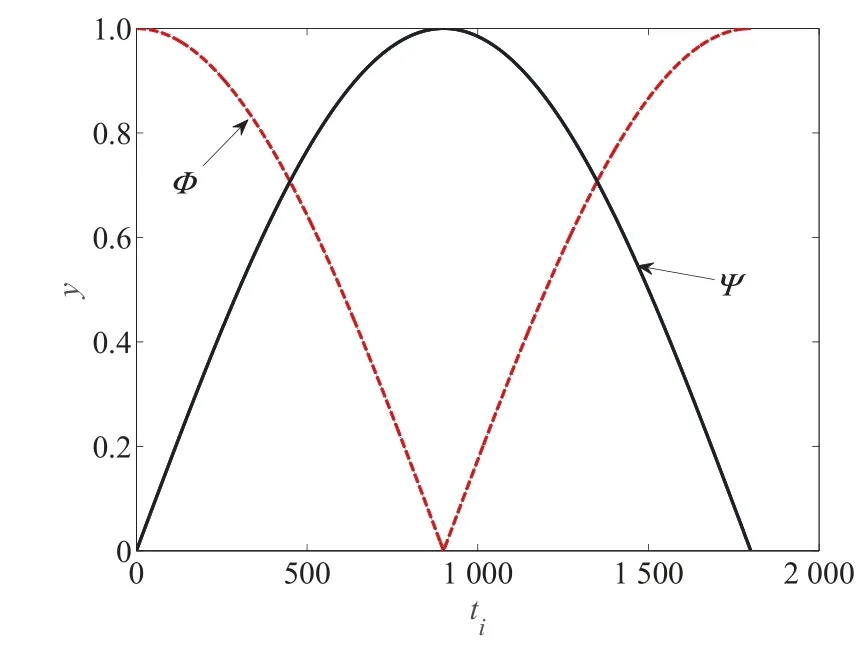
图1 调节算子和阈值曲线图Fig.1 The curve of regulation operators and limit

由图1 可以看出,在算法前期优化过程中,局部调节算子Φ大于全局搜索算子Ψ,蜜源更注重于局部开发;但在个体蜜源进化过程中,随着蜜源自身阈值的增加,全局搜索算子Ψ变大,精英解对蜜源的影响变大,加速收敛进程;最后,算法重新侧重于对局部开发的能力,保证在进化后期种群具有良好的分布性,以达到整个进化过程中局部搜索和全局开发能力的平衡.

3.2 基于个体分布的概率选择公式

在单目标优化问题中,在跟随蜂阶段只需要根据个体的函数值就可以计算蜜源的适应度值.但在多目标问题中,仅仅考虑个体的函数值,在一定程度上很难判断解的优异性,在进化过程中难以保证种群的分布性和收敛性.从图2 可以看出,由于A 点不支配任何个体,一旦蜜源A 在开发过程中被淘汰或因达到自身开发阈值被重新初始化时,种群的多样性将被破坏,将这种具有保障种群整体分布性的蜜源称为多样性个体.因此,本文提出一种基于种群个体分布的概率选择公式,通过充分考虑种群中个体的分布性,赋予多样性个体更高的适应度值,最后利用轮盘赌选择解引导种群进化,以获得一组收敛性和分布性良好的Pareto 最优解集.改进后的蜜源i的选择概率

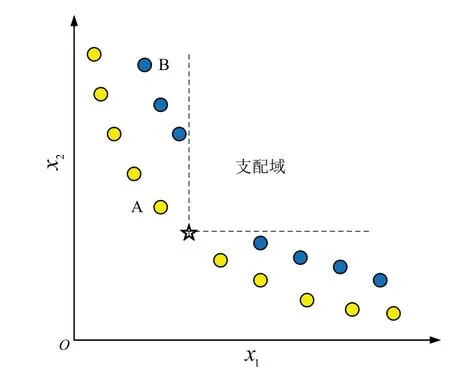
图2 多样性点示意图Fig.2 The picture of diversity point

其中F(i)为蜜源i的的适应度值,F(i) = (Riexp(2mi/N))−1,Ri表示蜜源i的支配等级,mi为蜜源i支配蜜源的数量,N为蜜源总数.

为了保持算法中种群的多样性,在式中将蜜源支配解的数量考虑到蜜源适应度的计算中.由式(4)可以看出,蜜源A 为非支配个体且mi为0 时,蜜源的适应度值为1.对于非支配个体,当蜜源支配解得数量越多时,其被赋予的适应度值越小,则其被选择引导进化的概率也就越小.而对于支配个体,由于其蜜源本身是被支配的,导致其具有先天性的劣势,其适应度值被限制在(0,1/Ri].通过考虑蜜源的分布性和支配等级分配蜜源适应度值的方式,在跟随蜂阶段多样性个体会有更高的概率被选择去引导蜜源进化,以保证整体算法的分布性,有利于改善算法的多样性和收敛性.

算法在跟随蜂阶段蜜源位置更新方法为

其中k=1,2,...,N/2 且k=i,j=1,2,...,D,r ∈[1,1.75],µ的计算方式同引领蜂阶段计算方式一致.

3.3 改进的外部档案维护策略

精英解即搜索过程中产生的非支配解,通过将精英解保存到外部档案中,并利用其信息引导种群进化,提高种群的收敛速度.一般条件下,外部档案具有固定大小(见图3).当外部档案为空时,将进化过程中产生的非支配解加入外部档案.当外部档案存储解的数量达到最大时,将个体的拥挤距离作为评判标准,将拥挤距离最小的个体删除,直到迭代结束获得一组满足数量的解(见图4).由图4 可以看出,根据传统的外部档案维护策略,E 点将会被删除,这样的做法将会造成D 点和G 点环境之间多样性的缺失,破坏了多样性.为了解决此问题,本文提出一种新的外部档案维护策略,当外部存档容量大于最大值时,将拥挤距离最小的E 点和距离其最近的F 点两者进行维度混合,重新生成一个新的个体,更新位置为xi= (xm+xn)/2,其中xm为将被删除的拥有最小拥挤距离的个体,xn为距离具有最小拥挤距离个体最近的点.

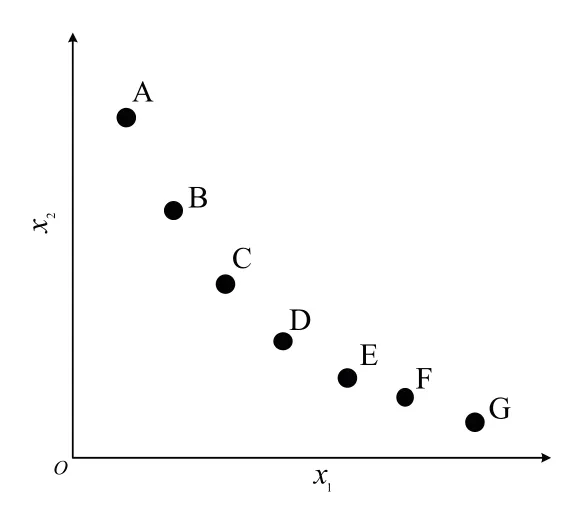
图3 外部档案Fig.3 External arhcive

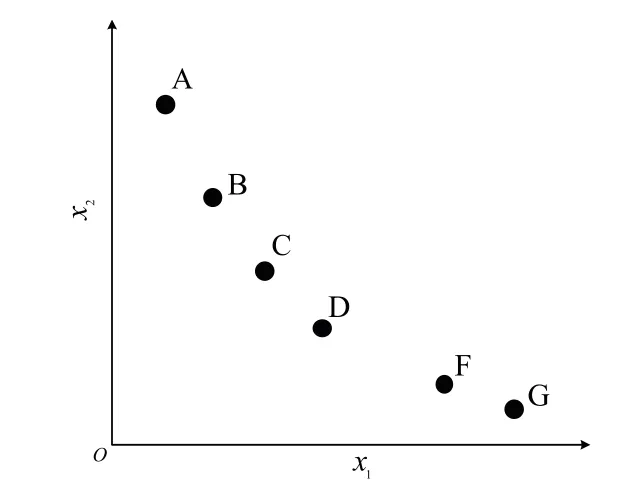
图4 截断后外部档案Fig.4 External arhcive after truncation

3.4 利用多样性点的重新初始化方式

为了充分利用多样性个体的信息,当蜜源达到开发阈值Limit 时,利用下式对蜜源进行初始化,

如果不存在多样性个体,则利用非支配个体的信息进行初始化,其中xi为重新初始化产生的新个体,xD为多样性个体,x为需要重新初始化个体.

3.5 算法步骤

本文提出的算法具体步骤如下:

步骤1初始化种群数量为N,外部档案最大存储量为N/2,设置最大评价次数Evaluation,侦查蜂的最大淘汰次数为Limit,并对蜜源进行初始化.

步骤2按照式(3)对引领蜂位置进行更新,更新后如果支配原始蜜源则被保留,且ti ←0,否则ti ←ti+1,并将新产生的解与外部档案中个体比较支配关系确定是否保留.

步骤3通过式(4)计算个体的适应度值和选择概率,并通过轮盘赌方法选择个体引导种群中个体进化,具体进化公式为式(5),并对其后代执行与引领蜂相同的保留策略.

步骤4判断当达到个体ti >Limit 时,通过式(6)重新初始化产生一个新蜜源来替换旧蜜源位置.

步骤5在每次迭代完成后,对外部档案进行维护,判断是否达到最大的评价次数Evaluation.若达到则结束循环并输出外部档案中的个体作为最终结果,否则转至步骤2.

4 实验仿真与分析

为验证本文算法的有效性, 与NSABC[17], S-MOABC/NS[15], MOABC[22]以及NSGAII算法[2]在10 个无约束多目标测试问题进行仿真.仿真采用Inter(R)Core(TM)i5-7500 CPU, 8G RAM 的PC 机, 实验环境为MATLAB R2017a.

4.1 测试函数及性能指标

本文针对两目标和三目标的优化问题进行测试,采用CEC09 测试集[25]中UF 系列测试函数,并将综合性指标inverted generational distance(IGD)[26]作为性能评价指标,即

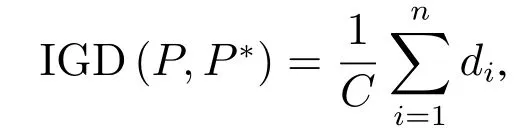
其中C为真实Pareto 前沿上解的个数,di为真实前沿PF 上第i个点到算法所求解集的最小欧氏距离.

IGD 指标通过计算真实Pareto 前沿与求得前沿之间的欧式距离,反映算法所求解集的分布性和收敛性.

4.2 仿真实验结果与分析

为了测试本文RMOABC 算法的性能, 选取了四个对比算法在UF1～UF10 上进行仿真, 算法的参数如表1 所示, 其余在算法中涉及参数全部参考原文献.表2 中统计了算法的IGD 最优值(best)、最差值(worse)、平均值(mean)和标准差(std),其中加粗项为同一测试函数中取得最优值.

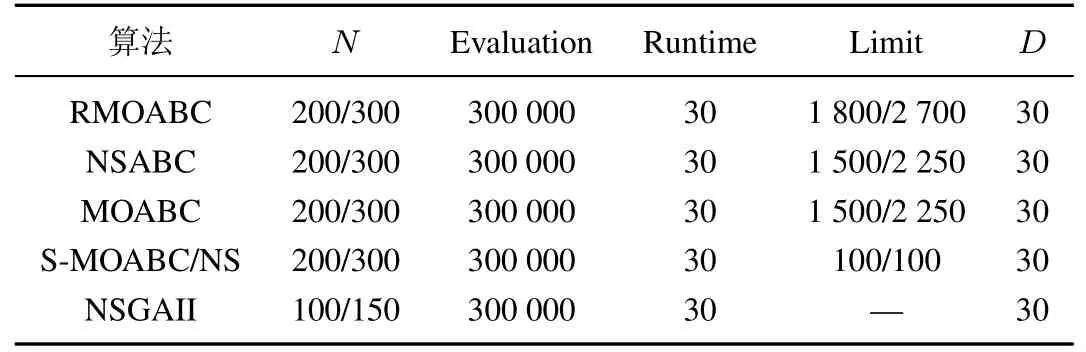
表1 参数设置Table 1 The parameter settings

从表2 中可以看出,本文所提出的算法无论在UF 系列的双目标还是三目标测试函数上,所提出的算法均可以获得良好的效果,且具有较小的标准差,说明RMOABC 算法在保证分布性和收敛性的同时,还可以保证良好的稳定性.

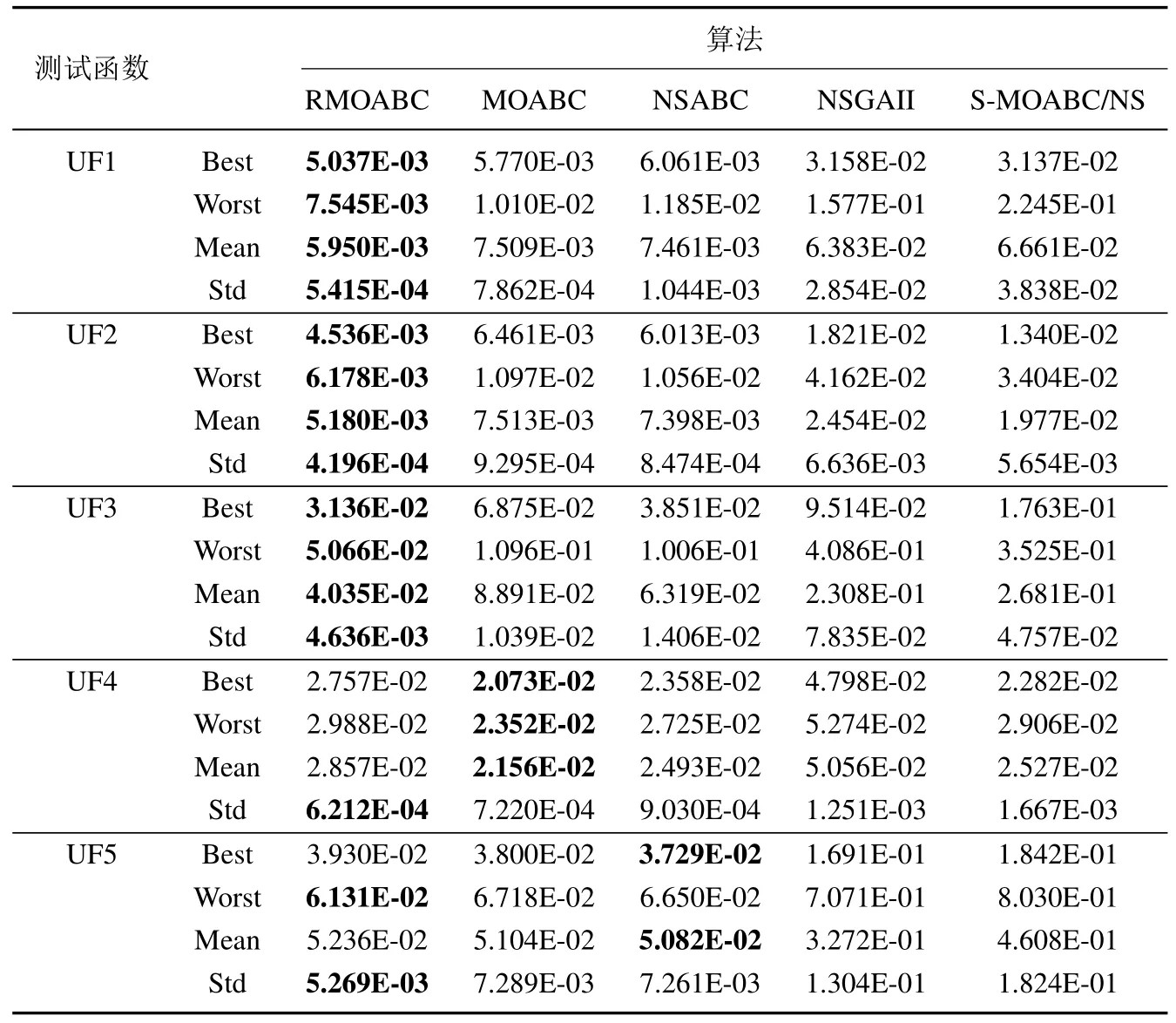
表2 算法IGD 值指标仿真结果比较Table 2 Comparison of algorithms via IGD-metric

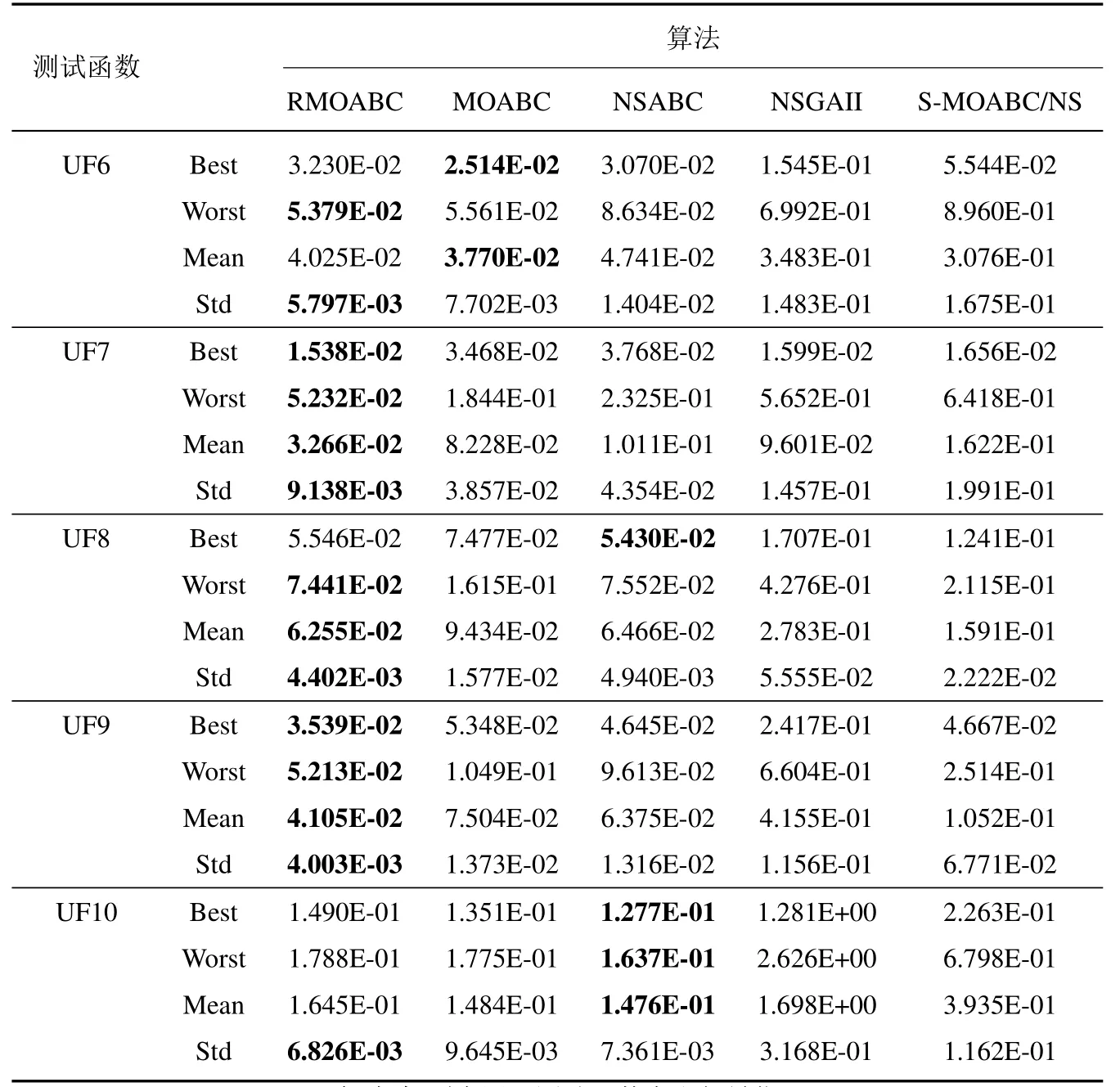
在双目标测试问题上(UF1～UF7),对于凸优化测试函数(UF1～UF3),RMOABC 算法均获得了较好的效果,说明RMOABC 算法在处理此类MOP 问题时相较于其他算更具有优势; 对于非凸测试函数UF4 以及具有非连续Pareto 面函数UF5,UF6 测试问题,虽然本文算法在IGD 平均值上落后于MOABC,NSABC 经典算法, 但RMOABC 在结果上与以上两种算法保持在同一数量级, 并且标准差优于以上两种算法, 说明在处理此类问题时具有良好的稳定性; 对于UF7 测试问题,虽然NSGAII 算法在分布性上优于RMOABC算法, 但是在收敛性上劣于RMOABC 算法, 说明RMOABC 算法具有较好的收敛性; 在三目标测试问题(UF8～UF10),除了在UF10 上劣于MOABC,NSABC 算法外,在其他两个测试问题无论是平均值还是标准差上,均取得了最好的结果,说明算法对比其余4种算法在处理三目标优化问题时具有良好的竞争力.

续表2Table 2 Continues

4.3 各策略IGD 值分析

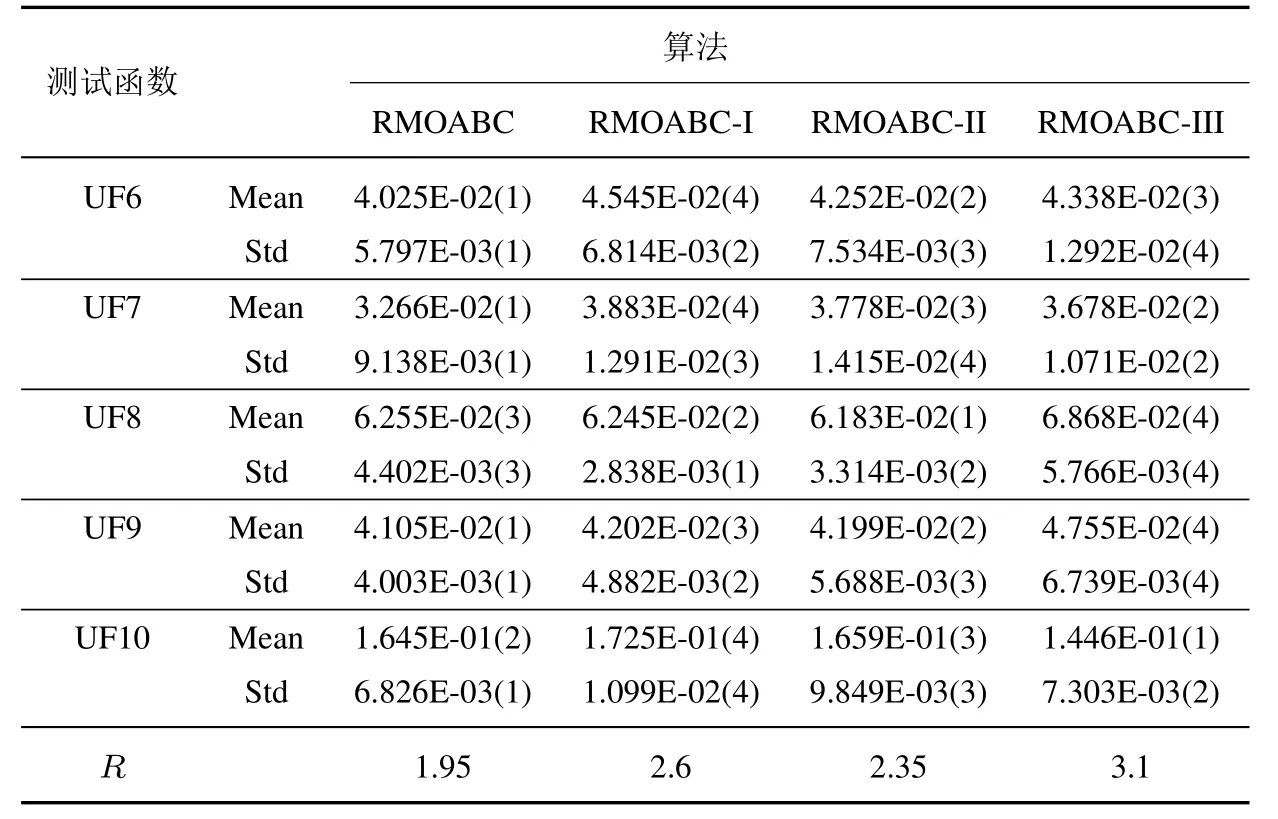
为了验证本文提出算法策略的有效性,本节设计3组对比实验,RMOABC-I 为标准蜂群算法适应度计算公式的算法,RMOABC-II 为采用一般的外部档案维护策略的算法,RMOABC-III 为采用标准人工蜂群算法搜索公式的算法.上述算法除部分策略不同,其余参数与4.1 节设置一致.

令R=其中n为测试函数的个数,ri表示算法在第i个测试函数上的排名.

表3 中给出四种算法的排名,其中R表示算法在10 个测试函数的平均排名,其值越小,表明算法表现的更优异.可以看出RMOABC 算法平均排名最小,表明基于3 种策略的RMOABC 算法性能更好.

由表2 和表3 可以看出本文提出的策略,无论是在收敛性和稳定性上都有较明显的提升.

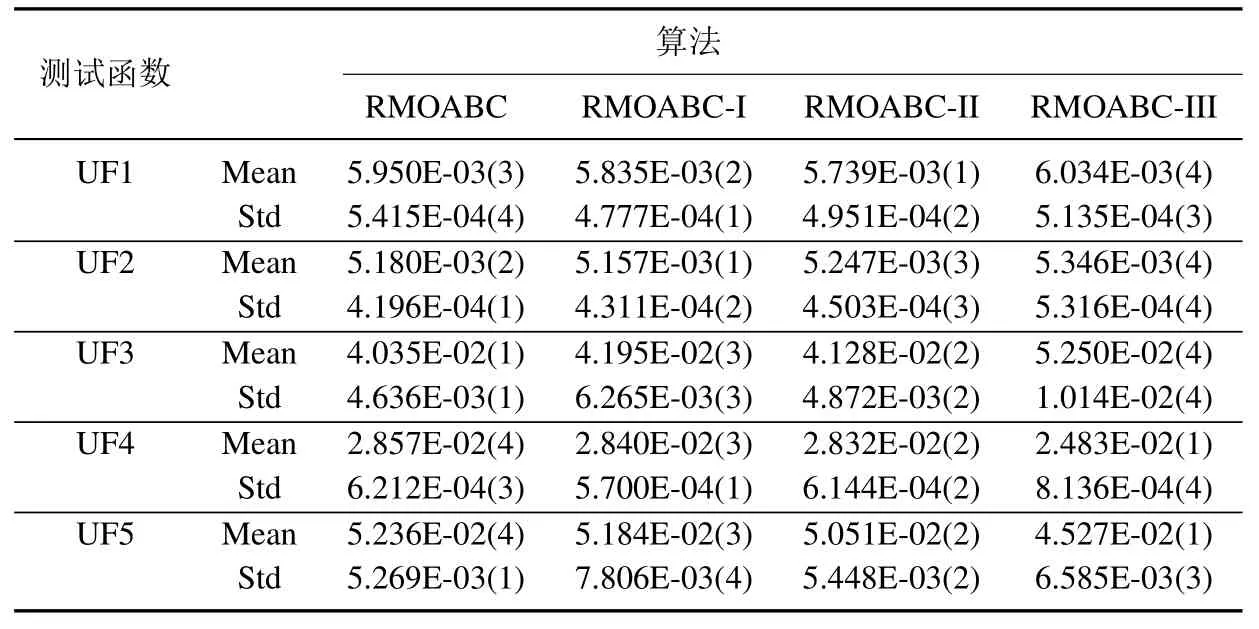
表3 不同策略算法IGD 比较Table 3 Comparison of algorithms based on different strategies via IGD-metric

续表3Table 3 Continues

4.4 算法收敛性分析

图5 中给出了RMOABC 和其余4种算法的IGD 下降趋势图,所选择的数据为UF 系列函数在30 次独立实验所获得的IGD 平均值.为了能够直观的看出下降趋势, 将IGD 对数作为纵坐标, 每评价105次记录一次数据,图中的虚线为5 种算法IGD 求和取平均值.对于双目标测试问题(UF1～UF7),在非凸测试函数UF4 和非连续测试函数UF6 中,RMOABC 算法分别排在第四位和第二位,除此之外相较于其它4 种算法,RMOABC算法都具有较快的收敛速度,且都比较稳定;对于三目标测试问题(UF8～UF10),在UF10 函数收敛速度劣于S-MOABC 以及NSABC,但另外两个测试函数上收敛速度和最终结果均优于其它4 种对比算法,说明RMOABC 算法在三目标问题上也能取得较好的结果.结合表2 和图5 的实验结果,RMOABC 算法在UF 测试问题相较于其他4种对比算法总体上具有显著的收敛性和分布性上的优势.

图5 算法收敛性能Fig.5 The convergence performance of algorithms

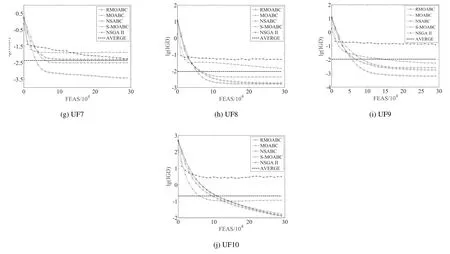
续图5Fig.5 Continues

5 结束语

为了达到加快算法收敛速度以及平衡全局搜索能力和局部开发能力的目的,本文提出了一种基于调节算子的多目标蜂群算法.首先,利用蜜源阈值生成的调节算子构成搜索公式,实现了对蜜源寻优方向的动态调节,根据蜜源自身情况精细控制,达到平衡全局搜索能力和局部开发能力的目的.其次算法在跟随蜂阶段计算概率时增加多样性蜜源被选择的概率,改善种群的分布性.最后算法采用新的外部档案维护策略,避免了多样性丢失的问题.通过RMOABC 算法与其它4 种代表性算法与10 个基准非约束多目标测试函数,在同一环境下进行仿真对比,结果表明本文的算法在分布性和收敛性方面有较好的提升.