基于应力和温度影响下沥青混合料蠕变模型*

安文静，盛冬发，张思成，刘邦剑，程家幸

(1. 西南林业大学 土木工程学院，昆明 650224； 2. 东南大学 土木工程学院，南京 211189)

0 引 言

沥青混合料是由沥青和骨料按照不同体积比混合而成。沥青混合料具有良好的热稳定性、耐磨性、耐腐性、可塑性等优点，已广泛地应用到路面铺设、材料绝缘、防腐和防水等领域。改革开放以来我国经济发展迅猛，要想富先修路的政策推动了交通行业的快速发展，作为路面主要铺设材料的沥青混合料得到了广泛应用[1-2]。近年来，随着物流行业迅猛发展特别是大型货车数量急剧增加，造成沥青路面松散、坑洼情况加剧[3]。研究表明，减小骨料平均粒径或者添加玄武岩纤维可以增强沥青混合料抵抗变形的能力[4-5]。众多学者利用Burgers模型、广义Maxwell模型或广义Kelvin等模型描述材料蠕变行为[6-8]。然而传统的Burgers模型不能很好地描述沥青混合料加速蠕变阶段[9]，将一个黏塑性元件与Burgers模型串联得到一个可以描述沥青混合料蠕变全过程的力学模型。随着Origin拟合软件不断完善，将蠕变实验数据与力学模型进行拟合可以较好地验证力学模型的适用性和有效性[10]。

开展沥青混合料蠕变行为的研究，可有效地揭示路面损坏的机理。国内外学者对沥青混合料蠕变行为进行了大量理论和试验研究。Lu[11]等通过Perzyno理论建立了沥青混合料本构方程，运用有限元软件编制有限元程序，计算结果显示该程序可以较好模拟沥青混合料永久变形发展过程。陈静云等[12]运用Matlab软件，将实验数据对模型进行拟合得到模型参数，利用Prony级数方法发现Burgers模型比广义Maxwell模型更能准确表达沥青混合料的本构关系。王游等[13]在Harris函数基础上建立一个非线性损伤黏性体，通过与Bingham模型串联得到一个非线性蠕变模型，利用1stOpt软件对模型拟合曲线与实验数据进行对比，结果表明该模型拟合曲线具有较高精度，可以用来拟合岩石蠕变全过程。张强勇等[14]基于不同应力、温度作用下的三轴压缩蠕变实验结果，建立了片麻状花岗岩热黏弹塑性损伤蠕变模型，分析了不同应力作用下温度对其蠕变的影响。通过正交实验，锁利军等[15]发现应力较温度对沥青混合料强度的影响更加明显。刘开云等[16]通过蠕变实验证明了改进的Bingham模型可以很好地反映岩石加速、减速蠕变阶段，为非线性蠕变模型提供了新的借鉴。董满生等[17]提出了一种考虑温度效应的力学模型，并将理论模型与实验结果进行拟合对比，结果表明该模型较传统的Burgers模型能更好地反映沥青混合料蠕变行为。Saboo[18]利用广义Burgers模型和实验数据对沥青混合料蠕变柔量进行预测。何兆益等[19]利用WLF方程，预测了沥青混合料的动态模量曲线。

作为一种经典黏弹塑性材料，应力和温度是影响沥青混合料蠕变行为的重要因素[20-22]。因此，开展不同应力或不同温度条件下沥青混合料蠕变性能的研究具有重要意义。为了探究应力和温度对沥青混合料蠕变性能的影响，本文首先构造了一个沥青混合料非线性黏弹塑性蠕变模型；然后分别进行不同应力和不同温度条件下沥青混合料单轴压缩蠕变实验；利用Origin软件，通过实验结果与蠕变模型拟合得到模型中待定力学参数；最后通过Origin软件中的多项式拟合功能，分别得到模型力学参数随应力或温度变化的关系式。该模型可以较好地预测沥青混合料在不同应力或不同温度作用下的蠕变行为。

1 沥青混合料蠕变模型及理论

1.1 Burgers模型

将Hooke体和Newton体串联得到Maxwell体(第I部分)。Hooke体和Newton体并联组成Kelvin体(第Ⅱ部分)。将Maxwell体和Kelvin体组合，可得到经典Burgers模型，如图1所示。

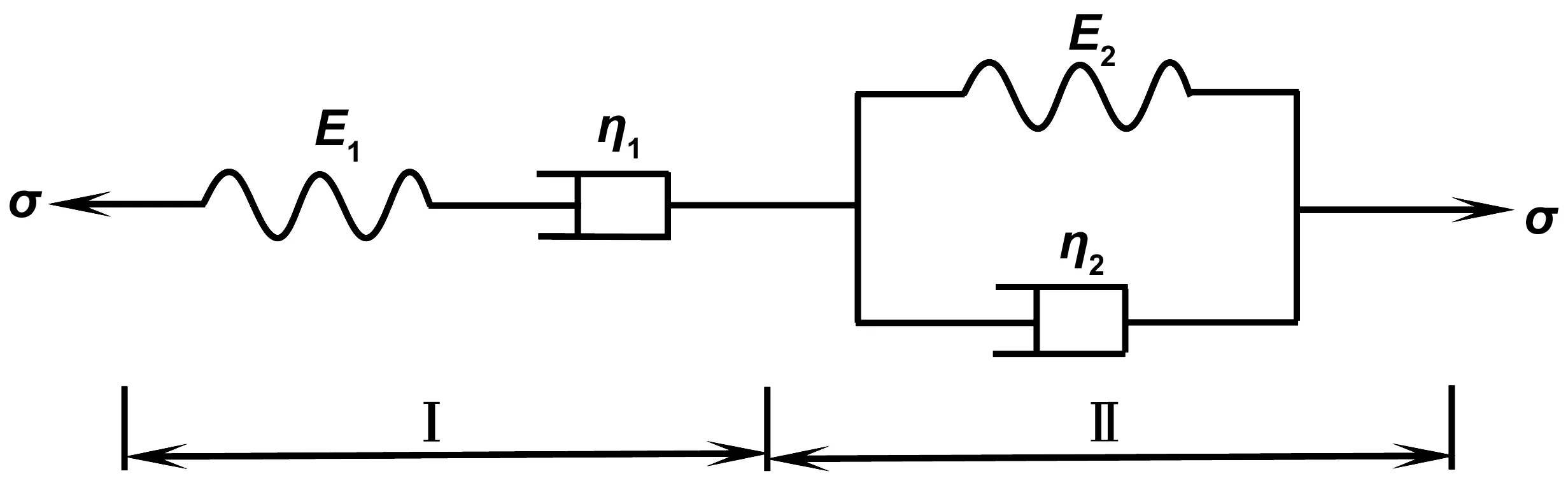
图1 Burgers模型Fig 1 Burgers model

沥青混合料作为一种黏弹塑性材料，受应力和温度作用蠕变特性明显。Burgers模型可以较好地反映沥青混合料的蠕变特性，其蠕变方程如下

(1)

式中E1、E2分别表示Maxwell模型和Kelvin模型中Hooke体对应的弹性模量，η1、η2分别表示Maxwell模型和Kelvin模型中Newton体对应的黏性系数，σ、ε表示Burgers模型的应力与应变。该模型的各个部分的应力相等，总应变是Ⅰ和Ⅱ两部分应变之和。

1.2 非线性黏弹塑性蠕变模型

Burgers模型可以较好地反映沥青混合料初期阶段和稳定阶段蠕变特性，但却不能很好地描述材料加速蠕变阶段。沥青混合料加速蠕变阶段是材料内部变形积累到一定程度后加速发展的结果，变形不断累积造成材料最终破坏。文献[23]、[24]通过将一个经典力学模型与黏塑性体串联，得到可以描述材料蠕变全过程的力学模型。为了更好地描述沥青混合料非定常蠕变阶段，本文在Burgers模型基础上串联一个黏塑性体组成一个六元件非线性黏弹塑性蠕变模型，如图2所示。

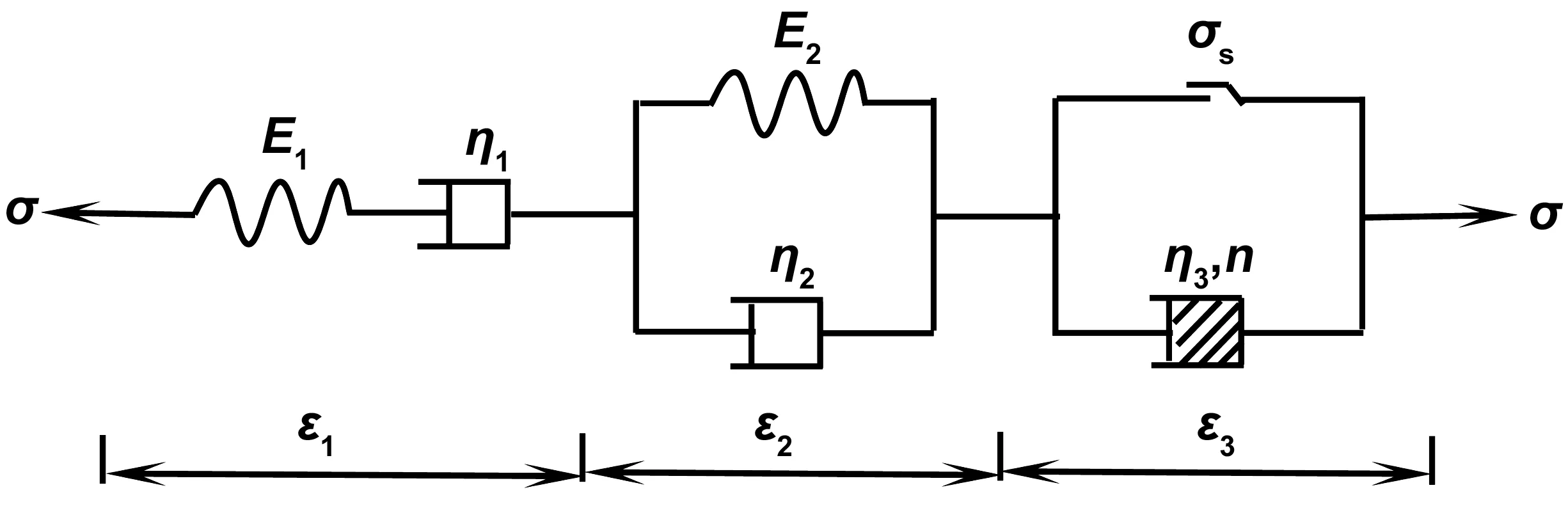
图2 六元件非线性黏弹塑性模型Fig 2 Six-element nonlinear viscoelastoplastic model

在此我们引入一个开关函数Γ

(2)

黏塑性元件的蠕变方程为

(3)

式中：σ是应力，σs是元件屈服应力(σ>σs时该等式成立)，η是元件黏性系数，n为蠕变指数(反映沥青混合料的加速蠕变速率)。

六元件模型的总应变为

ε=ε1+ε2+ε3

(4)

式中：ε1、ε2为

(5)

(6)

联立式(3)、(4)、(5)、(6)得到六元件非线性黏弹塑性模型的蠕变方程为

(7)

当σ0>σs，式(7)可以很好地描述沥青混合料的加速阶段蠕变行为。当σ0≤σs，式(7)将退化成Burgers模型。查阅文献[25]，可知沥青混合料应力极限σs在0.04～0.06 MPa之间。本文为了方便计算，取σs=0.05 MPa。

2 沥青混合料蠕变实验及模型参数计算

2.1 蠕变实验

将粒径在1.18～2.36 mm砂粒和型号为AH-70沥青按照62∶38比例制成沥青砂混合料。实验材料的不均匀性会导致实验结果出现偏差，为了减小实验误差，本次实验将试件压缩成高50 mm、半径25 mm的圆柱体。处理后试件表面没有明显突起、不均匀现象。将制好的试件分成2个批次，每批4组每组5个。将第一批试件放入40 ℃实验温度箱内1 h使试件整体温度尽量接近实验温度，并在型号为AG-Xplus50 kN带有环境温度控制箱的力学试验机上进行沥青混合料蠕变实验。4组试件加载应力分别为0.10、0.20、0.25、0.30 MPa。将第二批4组试件分别放置到5、15、25、40 ℃实验温度环境中，加载应力恒定在0.10 MPa。

将试件在40 ℃恒定温度条件下进行不同应力的单轴压缩蠕变实验，利用origin软件中自定义拟合功能，将实验数据与六元件非线性黏弹塑性模型进行拟合，拟合曲线如图3所示。从图3中可以看出，蠕变曲线呈现出明显非线性，且曲线斜率随加载应力的增大而增大。该模型曲线与实验数据吻合较好，表明该模型的正确性。

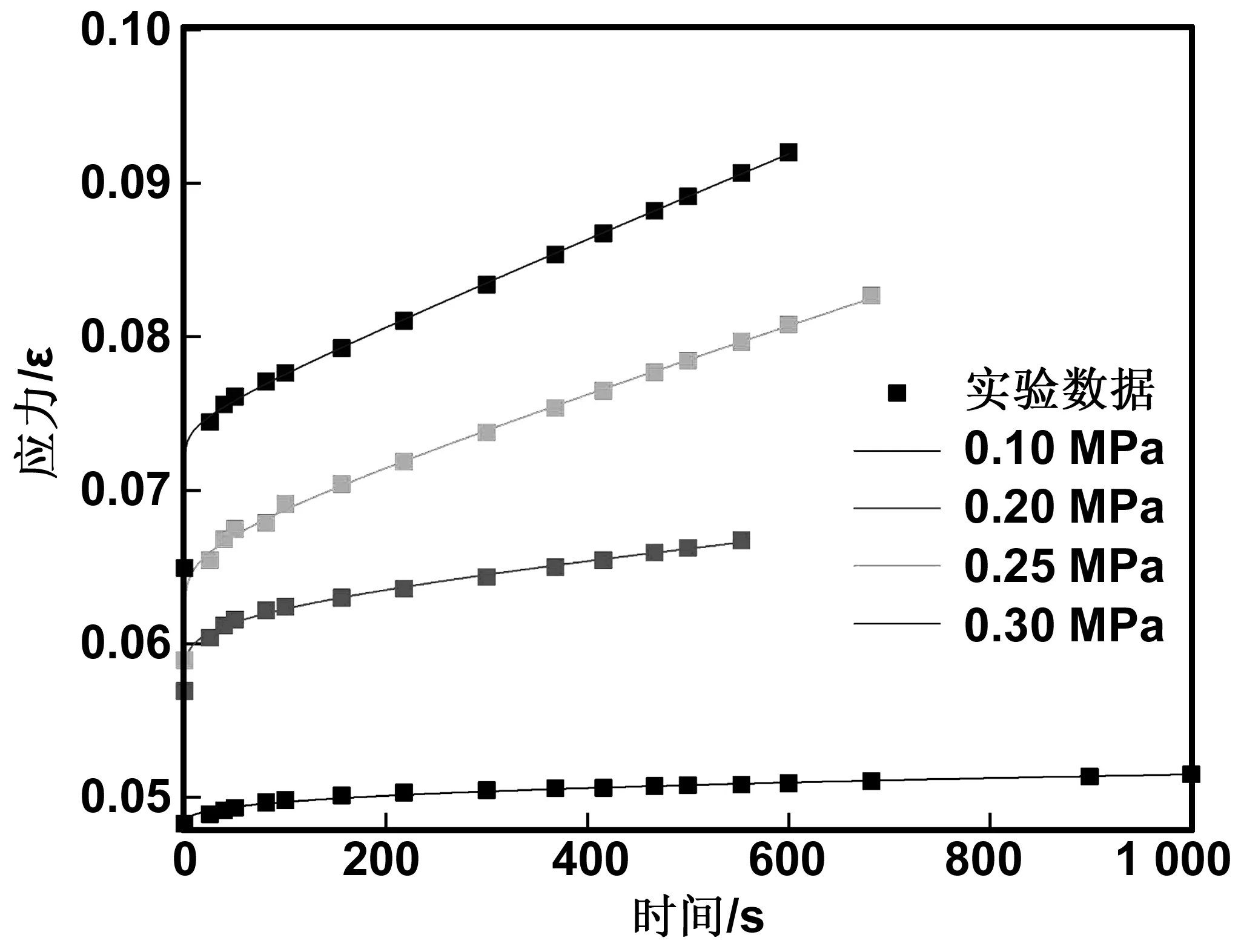
图3 不同应力下沥青混合料蠕变曲线Fig 3 Creep curve of asphalt mixtur under different stresses

将试件在0.10 MPa应力不变条件下进行不同温度单轴压缩蠕变实验，利用origin软件中自定义拟合功能，将实验数据与六元件非线性黏弹塑性模型进行拟合，拟合曲线如图4所示。从图4中可以看出，曲线显现出明显非线性，且蠕变速率随温度升高而增大。与不同应力作用下的蠕变曲线类似，说明沥青混合料蠕变性能受应力与温度的影响较明显。

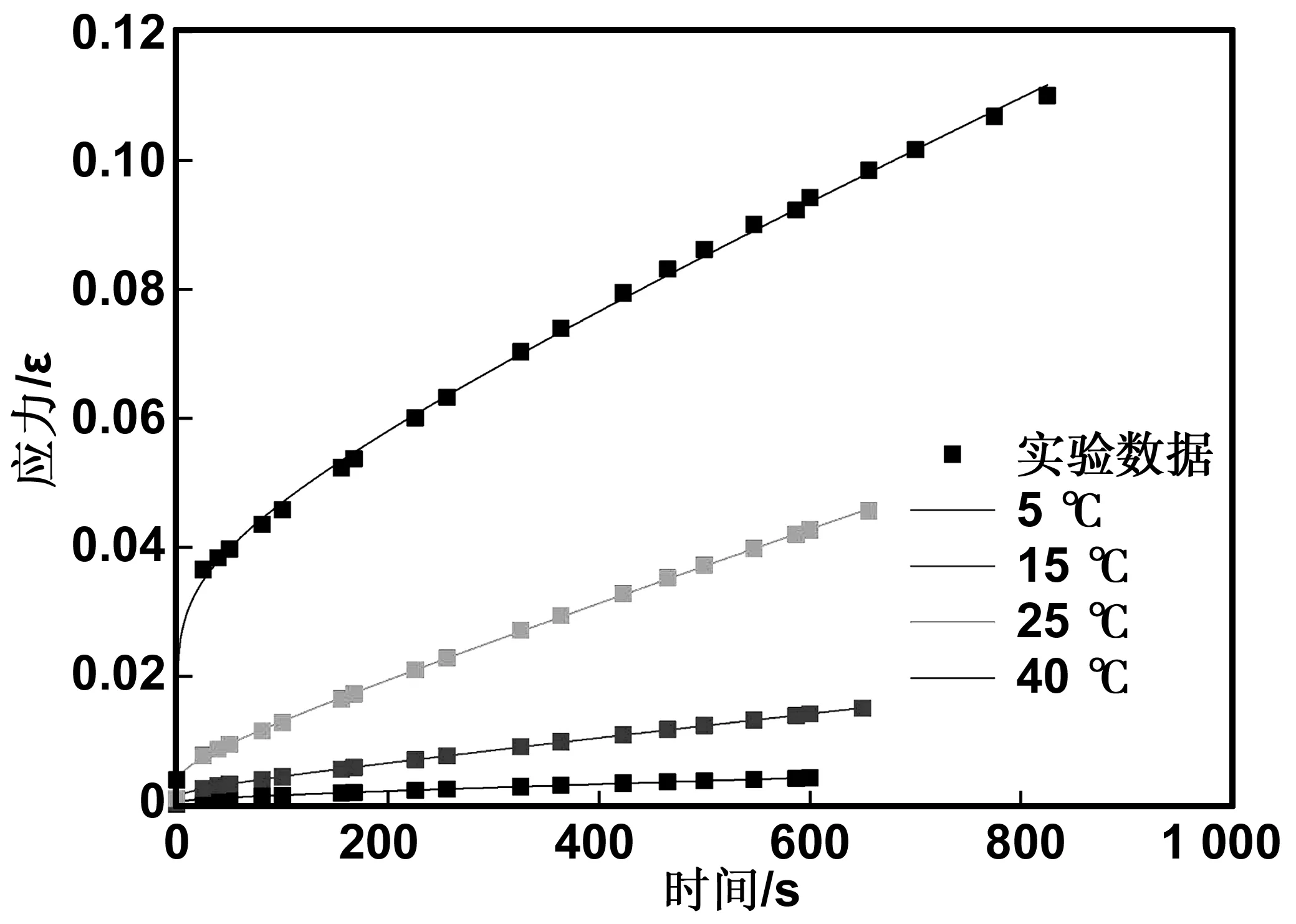
图4 不同温度下沥青混合料蠕变曲线Fig 4 Creep curve of asphalt mixture under different temperatures

2.2 模型参数拟合结果

该六元件非线性黏弹塑性模型有6个待定参数，它们分别为E1、E2、η1、η2、η3、n。通过对实验结果与模型进行拟合，可以得到沥青混合料在不同应力作用下和在不同温度条件下模型的待定参数，拟合结果如表1和表2所示。

表2 沥青混合料在不同温度条件下模型参数Table 2 Model parameters of asphalt mixture at different temperatures

3 考虑应力和温度效应的模型参数

3.1 考虑应力效应的模型参数

为了考虑应力效应，我们假设该非线性黏弹塑性蠕变模型的6个参数与应力存在着某种函数关系。利用Origin软件的多项式拟合功能，我们可以通过表1中的数据得到这些模型参数随应力变化的关系式，拟合结果如式(8)。

表1 沥青混合料在不同应力作用下模型参数Table 1 Model parameters of asphalt mixture under different stresses

(8)

利用上述关系式可以得到分别画出6个模型参数的拟合曲线，如图5所示。从图中可以看出，在温度恒定条件下，E1和η2随着应力的增加而总体上具有增大的趋势，E2、η1、η3、和n随着应力的增加而总体上具有减小的趋势。说明可以通过提高E1和η2两个模型参数，减小E2、η1、η3、和n4个模型参数，来提升沥青混合料的抗压能力。

图5 拟合参数与应力关系曲线Fig 5 The relationship curve between fitting parameters and stress

3.2 考虑温度效应的模型参数

为了考虑温度效应，我们假设该非线性黏弹塑性蠕变模型的6个参数与温度存在着某种函数关系。通过Origin软件的多项式拟合功能，我们可以通过表2中的数据得到这些模型参数随温度变化的关系式，拟合结果如式(9)。

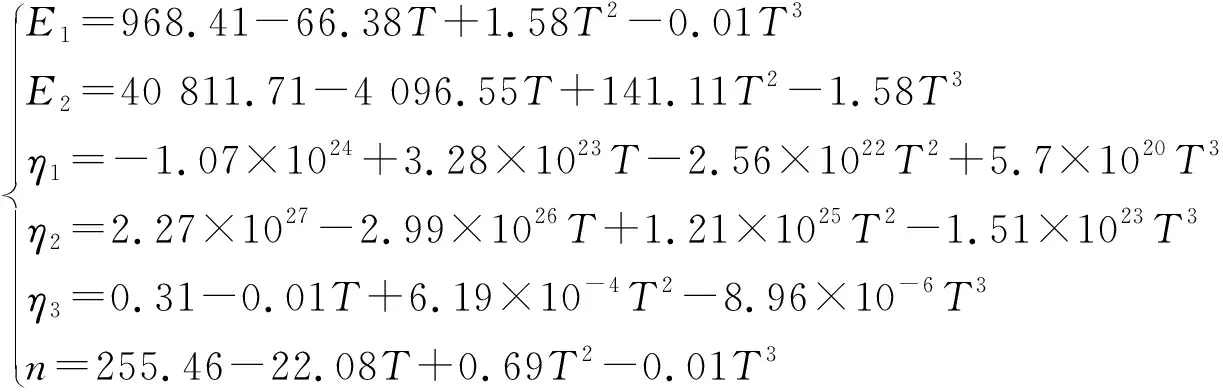
(9)

利用上述关系式可以分别画出6个模型参数的拟合曲线，如图6所示。从图中可以看出，在应力不变条件下，E1、E2、η2、η3和n随着温度的增加而减小，而η1随着温度的增加而增大。说明温度升高将使Maxwell体和Kelvin体的弹性模量均减小，Kelvin体和塑性体的黏性系数均减小，而Maxwell体的黏性系数将增大。说明温度的升高将使Maxwell体弹性变形增大，而Kelvin体和塑性体的黏性变形也将增大。在一定的载荷作用下，当温度升至较高时，引起材料的弹性形变主要由Maxwell体产生，而引起材料的黏塑性变形主要由Kelvin体和塑性体产生。

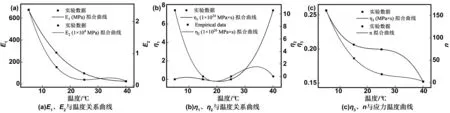
图6 拟合参数与温度关系曲线Fig 6 The relationship curve between fitting parameters and temperatures

观察式(8)和式(9)发现，非线性黏弹塑性蠕变模型中的力学参数与应力和温度存在着一定的函数关系。通过确定这些关系式可以预测不同应力和不同温度作用下的模型参数，进而预测沥青混合料的蠕变行为，从而节约实验成本，为沥青混合料的蠕变研究提供便利。

3.3 参数模型预测

为了验证模型的适用与正确性，我们对实验温度40 ℃，加载应力0.15 MPa时的蠕变曲线进行预测。将选取温度和应力代入式(8)，运用origin软件的绘图功能得到蠕变预测曲线如图7所示。图7可以看出，在相同温度条件下，预测曲线介于0.10和0.20 MPa之间，且蠕变曲线变化规律和由实验得到的0.10和0.20 MPa时的蠕变曲线的变化规律相同，说明预测结果较好。我们再对实验温度35 ℃，加载应力0.10 MPa时的蠕变曲线进行预测。将选取温度和应力代入式(9)，运用origin软件绘图功能得到蠕变预测曲线如图8所示。图8可以看出，在相同的应力作用下，预测曲线介于25和40 ℃之间，且蠕变曲线变化规律和由实验得到的25 ℃和40 ℃时的蠕变曲线的变化规律相同，表明预测结果较好。从图7和8可以看出，预测曲线符合沥青混合料的蠕变趋势，表明该蠕变模型可较好地预测沥青混合料的蠕变行为。

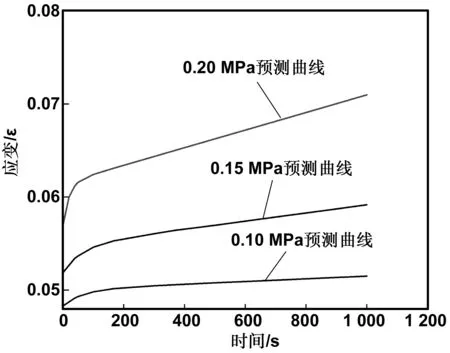
图7 40 ℃、0.15MPa条件下蠕变预测曲线Fig 7 Creep prediction curve at 40 ℃ and 0.15 MPa

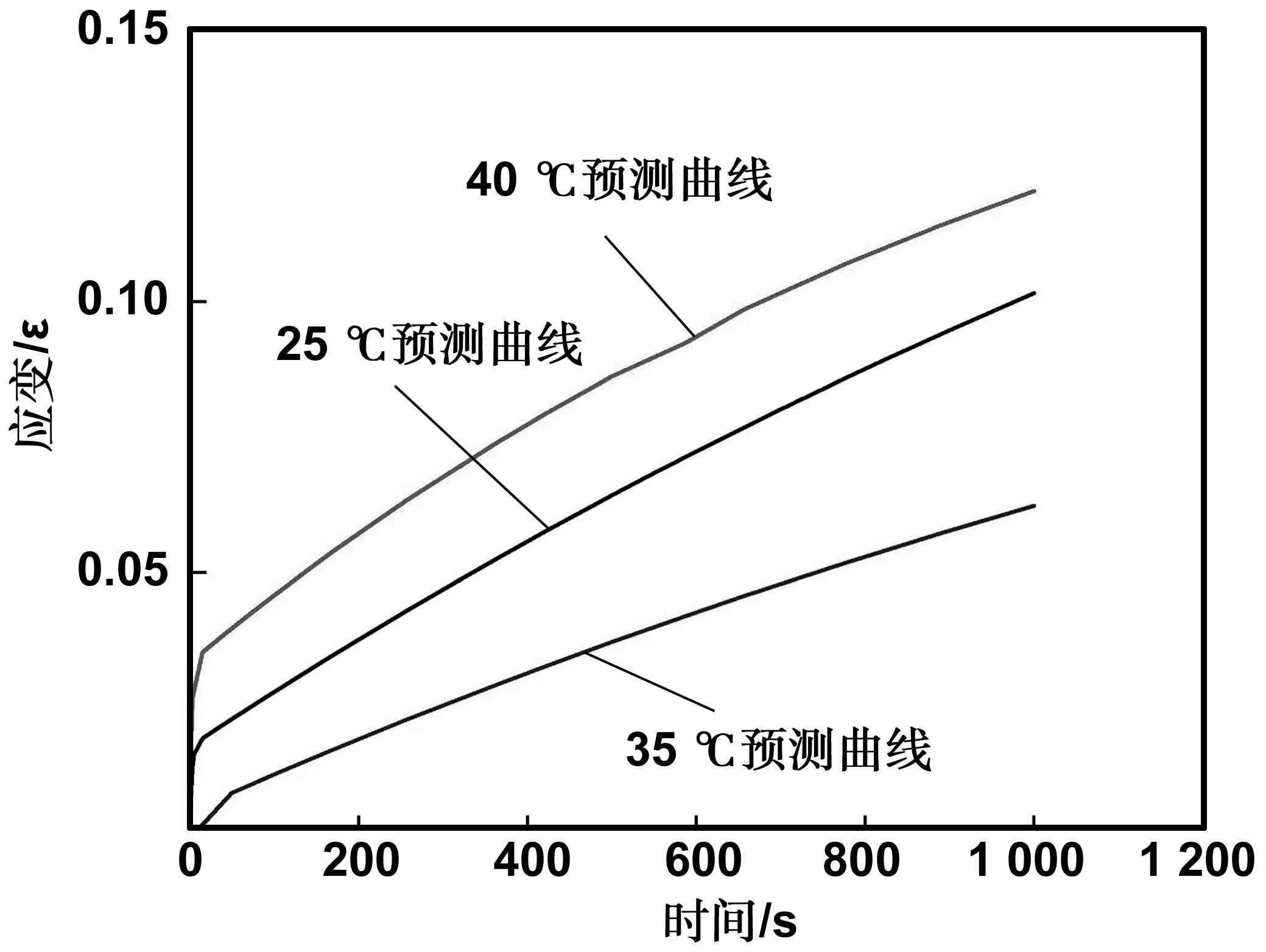
图8 0.10 MPa、35 ℃条件下蠕变预测曲线Fig 8 Creep prediction curve at 0.10 MPa and 35 ℃

4 结 论

(1)提出了一个可以描述沥青混合料蠕变全过程的六元件非线性黏弹塑性模型。通过不同应力和不同温度作用下的单轴压缩蠕变实验，利用origin软件拟合确定了E1、E2、η1、η2、η3、n6个模型参数。拟合相关系数大于0.98，表明沥青混合料蠕变模型具有较高的拟合精度和较强的适用性。

(2)通过origin软件多项式拟合功能，对不同应力和不同温度作用下蠕变模型参数进行拟合，得到这些模型参数随应力或温度变化的关系式。从拟合曲线可以看出，应力和温度对沥青混合料蠕变模型参数有明显影响。

(3)利用模型参数随应力或温度变化的关系式，可预测不同应力或不同温度作用下沥青混合料蠕变行为，进而为该材料蠕变行为的研究提供一定的理论基础。预测结果表明该模型可以较好地反映沥青混合料的蠕变规律，可对不同应力或不同温度条件下沥青混合料的蠕变行为进行较好地预测。