基于应力敏感的稠油油藏变启动压力梯度渗流模型与数值模拟研究

姜瑞忠，倪庆东，张春光，张凤博，郜益华，蔺靖淇

（1.中国石油大学（华东）石油工程学院，山东青岛 266580；2.中海石油（中国）有限公司上海分公司，上海 200335；3.中海油研究总院有限责任公司，北京 100028）

稠油油藏储量在未动用油藏中占比较大，具有较高的开发潜能［1-2］。基于稠油油藏黏度高、渗流阻力大的特点［3］，考虑变启动压力梯度的数值模拟研究用于稠油油藏开发［4］。张跃雷通过测量不同黏度稠油的流变性，对启动压力梯度与塑性黏度之间的关系做出了进一步的确定［5］。王泊等分别用数学模型以及实验的方法对非线性渗流启动压力梯度进行研究［6-7］。张芹月提出启动压力梯度与流度之间存在幂律关系［8］。张代燕等通过对实验数据进行回归，得到了有关启动压力梯度的经验公式［9］，并且提出稠油流动的非线性程度可用启动压力梯度来表征［10］。刘英宪等基于压敏效应得出启动压力梯度与生产井产量之间的关系［11-13］，同时严利咏等也提出启动压力梯度和压力敏感系数对地层压力的影响较为显著［14-15］。通过对特低渗透油藏的研究，李承龙等考虑压敏效应与启动压力梯度会对生产指标有显著影响［16-19］。目前稠油油藏非线性渗流数值模拟方法在模型求解过程中，未同时考虑储层的非均质性以及压敏效应和启动压力梯度变化［20-22］，一些简单的模型难以解决现场复杂区块的生产状况。

为此，笔者基于储层的非均质性以及稠油油藏在多孔介质中表现出非达西渗流的特点，应用启动压力梯度表征的油相视黏度与流动修正系数，描述稠油油藏黏度异常的现象，将压力梯度处理成与流度相关的变量并考虑其方向性，同时在考虑压敏效应的基础上建立全隐式数值模型。对模拟器进行相关测试并对典型稠油油藏区块进行数值模拟，探究启动压力梯度和压敏效应对稠油油藏开发生产指标的影响。

1 稠油油藏渗流实验规律

Y 油田是典型的高孔高渗透、高原油黏度的稠油油田。其渗透率为63.5～4 524.9 mD，原油黏度为13～424 mPa∙s，低黏度原油在总储量中所占比例较小。为了提高数值模拟的准确性，从Y 油田选取2个断块来研究不同储层条件下原油的临界黏度以及不同流度下的启动压力梯度。

通过岩心取样，在岩心渗透率和黏度随机的情况下测量了启动压力梯度。若不能测得启动压力梯度，则需增加其黏度，直到实验能测得启动压力梯度为止；若一开始就存在启动压力梯度，则其黏度应降低，直至启动压力梯度消失。通过对实验数据的回归分析，确定了不同黏度条件下原油的临界黏度［23］（图1）：不同渗透率的岩心启动压力梯度所对应的临界黏度不同，且临界黏度随岩心渗透率的增加而升高，增加范围趋于平缓。当临界黏度位于曲线的上方时，说明此时在稠油油藏中存在启动压力梯度，该启动压力梯度存在的临界黏度约为47～54 mPa∙s。

图1 临界黏度与渗透率的关系Fig.1 Relationship between critical viscosity and permeability

为了进一步确定启动压力梯度与稠油流动的关系，通过Y 油田2 个断块矿场试验中的启动压力梯度与流度的变化关系可得，稠油油藏渗流曲线的早期弧度不明显、过渡较快，当驱替压力梯度达到稠油油藏流动的临界值后原油即按拟线性渗流段流动，因此通常将启动压力梯度处理成流度的乘幂关系［24］。从图2 可以看出：启动压力梯度与流度之间有着明显的乘幂关系，且随着流度的减小，启动压力梯度先缓慢变大，当流度减小到临界流度时，启动压力梯度迅速增加，所以在评价稠油油藏流动时可用流度的乘幂关系处理启动压力梯度。

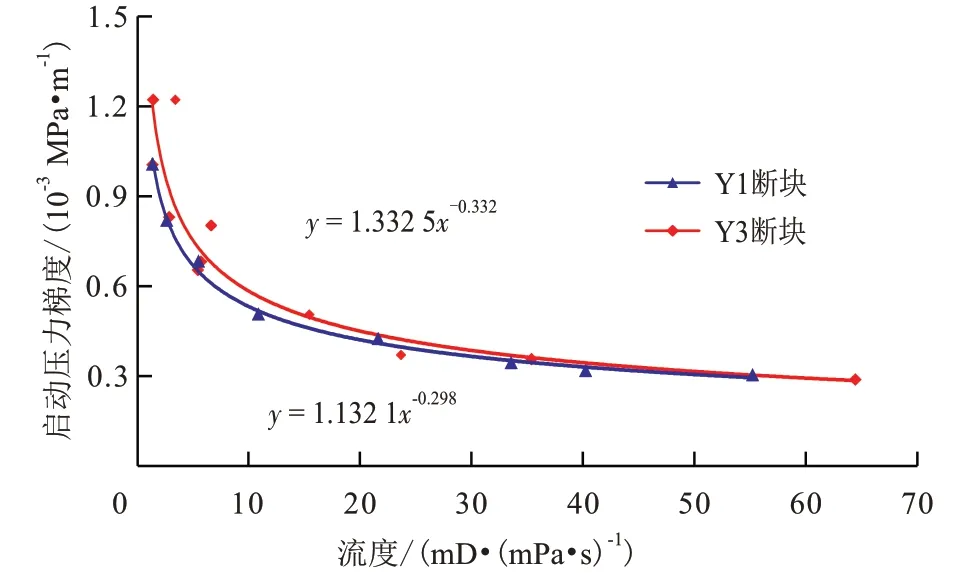
图2 启动压力梯度与流度的关系Fig.2 Relationship between starting pressure gradient and fluidity

2 渗流数学模型

2.1 模型建立

稠油油藏非线性渗流数值模拟的关键就是变启动压力梯度和压敏效应如何在模型中具体表征，建立数学模型的基本假设包括：①气体溶解于油水两相并且油水两相不互溶。②稠油油藏在渗流过程中为等温渗流。③考虑油相的启动压力梯度且气、水两相仍满足达西定律。④考虑毛管压力和重力。⑤考虑压敏效应的影响。

鉴于储层的非均质性，同时基于压敏效应将渗透率处理成与压力有关的函数，所以油、气、水相3组分的运动方程式分别为：

由于稠油油藏储层的启动压力梯度主要由黏度异常引起［25-26］，引入油相流动修正系数与油相视黏度来解释稠油油藏的黏度异常，在此基础上考虑了流动修正系数的方向性。根据实际情况，油相流动修正系数定义为：

油相视黏度可表示为：

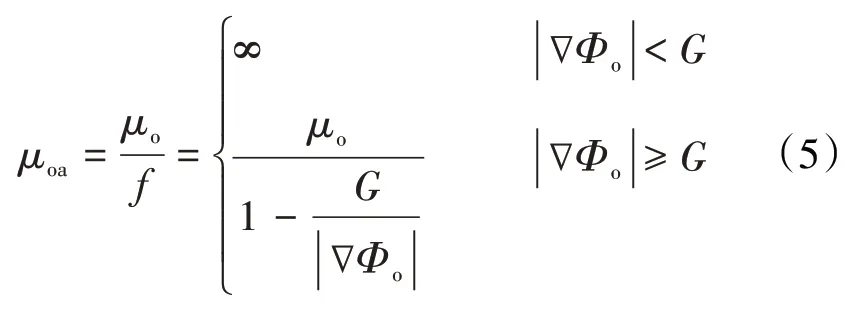
为了实现非均质油藏的客观模拟，基于油相的运动方程并结合启动压力梯度与流度的变化关系模型，得到稠油油藏启动压力梯度的表达式为：

2.2 模型求解

渗流方程 结合运动方程与连续性方程得到流动方程，通过转化形式并添加定解条件形成完整的油、水、气相组分的数学模型分别为：

辅助方程 饱和度与毛管压力方程分别为：

初始条件 初始压力和饱和度分别为：

边界条件 外边界条件（封闭）表达式为：

通过有限差分对已建立的三维三相数学模型进行油、气、水相3 组分的隐式差分，其表达式分别为：

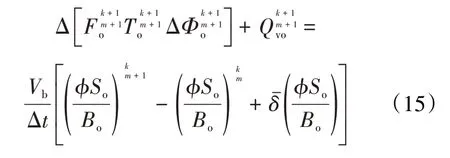
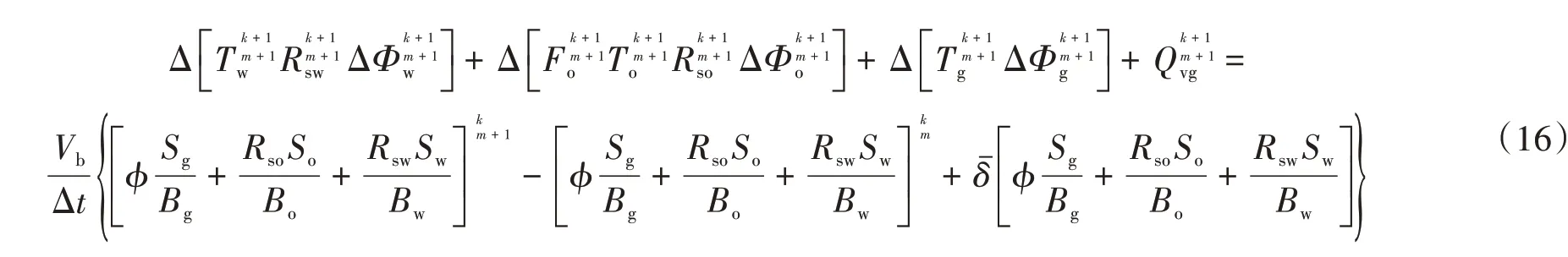
对油、气、水相3 组分的隐式差分方程展开，在m+1 个时间步长和k+1 个迭代步长的计算中，忽略Δ［（···）δSw］·Δ［（···）δpo］和Δ［（···）Δpo］·Δ［（···）δpo］等二阶小量，并整理上述方程式。将输出项代入模型，并求解未知数为δpo，δSw和δSo的块元素矩阵方程。通过以上步骤，建立了渗流微分方程的数值模型，并对流量校正系数等参数进行了处理，最终实现了全隐式解。

3 模拟器编制与测试

3.1 模拟器编制

稠油油藏变启动压力梯度数值模拟计算流程（图3）主要包括：①确定稠油油藏区块的物性参数并建立稠油油藏变启动压力梯度的数值模拟模型。②初始化压力和饱和度场。③采用全隐式迭代方法求解稠油油藏区块的压力和饱和度。④进行收敛条件与物质平衡检查。⑤检查是否达到模拟结束时刻，是则输出稠油油藏区块的启动压力梯度场、压力场以及饱和度场，否则重复上述步骤。

图3 数值模拟计算流程Fig.3 Flowchart of numerical simulation

3.2 模拟器测试

软件成功编译后，对软件进行黑油模型测试以及非线性和压力敏感模型测试，以满足软件在工程计算中的需求，无论是黑油还是非线性模型验证，均可通过对机理模型和实际模型进行多维测试来实现。

3.2.1 黑油模型测试

为了验证新开发模拟器的合理性和准确性，主要从对称性与ECLIPSE 开发指标的对比利用软件进行测试。建立了与稠油油藏油层特征相吻合的反五点机理模型A，用于模拟验证。该模型的主要参数包括：储层大小为310 m×310 m×15 m；网格大小分别为Δx=Δy=10 m，Δz=3 m；深度为1 500 m；机理模型共有5个小层，各层的渗透率在x，y，z方向上分别为：1-2 层为1 500 mD×1 500 mD×150 mD，3-4层为1 200 mD×1 200 mD×120 mD，5层为1 000 mD×1 000 mD×100 mD；孔隙度为0.34；水的密度为1.00 g/cm3，油的密度为0.93 g/cm3；水的黏度为0.50 mPa·s，油的黏度为100 mPa·s；水的体积系数为1.05，油的体积系数为1.15。井距为250 m，水井注入速度为160 m3/d，油井定产液量为40 m3/d，保持注采比为1∶1，模拟10 a，在均质模型中建立对称井网模式，设置每个井网的相同参数，并观察压力场和饱和度场是否对称。通过数值模拟研究，饱和度场和压力场随时间步的变化仍具有较好的对称性（图4），且生产井周围未波及区的形状也相同，证明了模拟器的计算结果可靠稳定。

图4 模型A饱和度场和压力场分布Fig.4 Distribution of saturation field and pressure field in Model A

当自研模拟器达到稳定性要求后，为了验证新开发模拟器的合理性与准确性，通过ECLIPSE 等商业软件和自研模拟器分别计算同一个模型，查看模拟结果的误差，判断自研软件的稳定性与精度。通过比较产油速度和含水率，可发现2 个模拟器的误差均较小，证明了自研模拟器具有合理性和准确性（图5，图6）。

图5 自研模拟器与ECLIPSE计算的区块日产油量对比Fig.5 Comparison between oil production rates calculated by self-developed simulator and ECLIPSE

图6 自研模拟器与ECLIPSE计算的区块含水率对比Fig.6 Comparison between water cuts calculated by selfdeveloped simulator and ECLIPSE

3.2.2 线性与非线性模型对比

自研模拟器的合理性与准确性达到要求后，为了测试软件的创新型，将Y3区块启动压力梯度与流度的关系曲线代入模型A 中，并且加入非线性关键字，通过压力场与饱和度场的变化体现变启动压力梯度的影响，压力场与饱和度场如图7所示。

图7 非线性模型的饱和度场和压力场分布Fig.7 Distribution of saturation field and pressure field in nonlinear model

压力场与饱和度场的变化表明，启动压力梯度的存在相当于稠油油藏驱替过程中的一个附加阻力，从而对累积产油量、含水率等指标产生巨大影响，导致开发效果变差。分别在考虑与不考虑启动压力梯度2 种情况下模拟，并将开采指标进行对比（图8）。启动压力梯度对生产指标影响显著：从含水率指标来看，启动压力梯度的存在会加剧水相的指进现象，加快生产井见水时间；同时考虑启动压力梯度会降低累积产油量，影响最终采收率，开发效果变差。

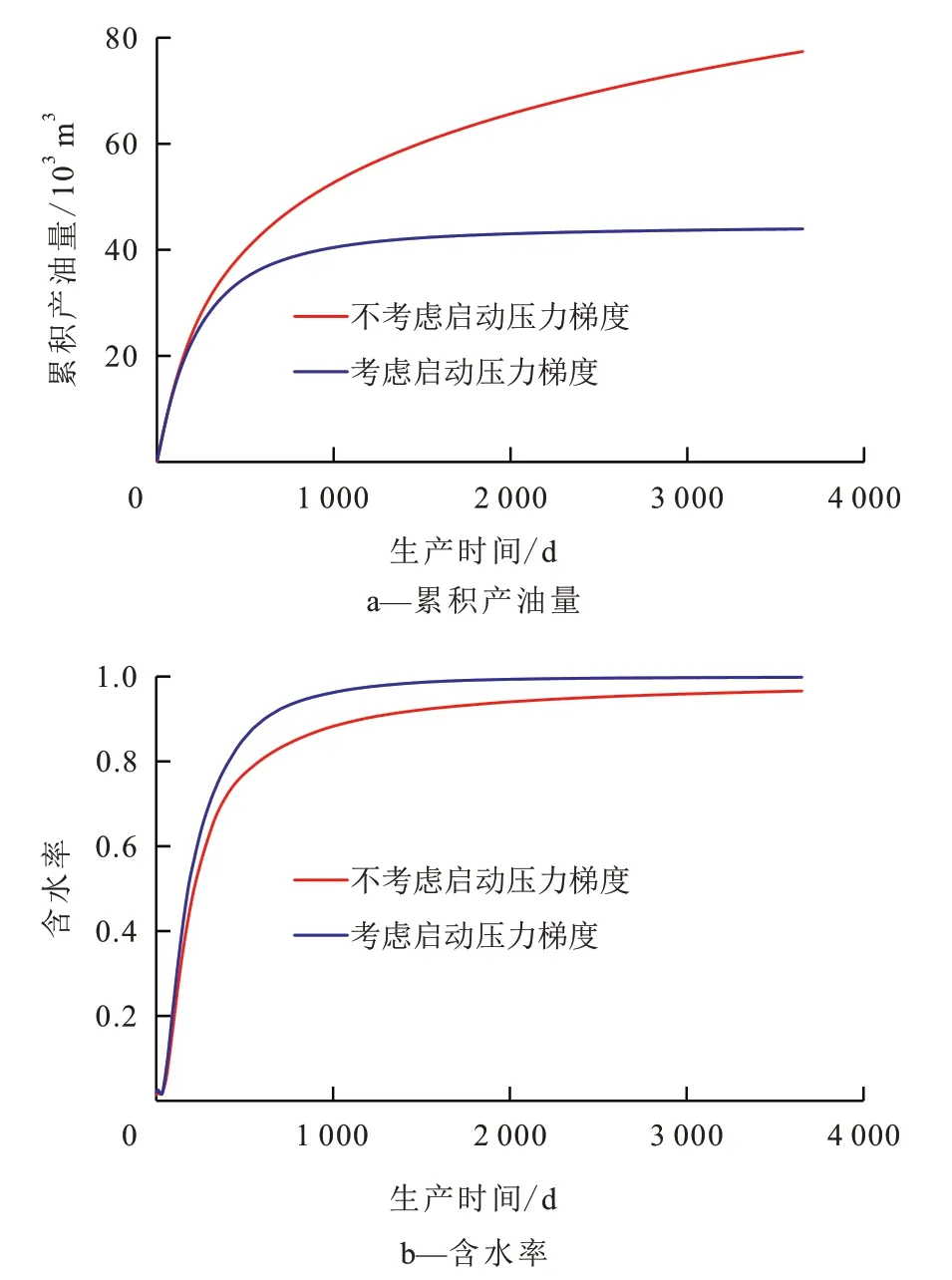
图8 启动压力梯度对生产指标的影响Fig.8 Influence of starting pressure gradient on production index

3.2.3 压敏效应的影响

自研模拟器的创新点不止在于考虑启动压力梯度对稠油油藏的影响，同时考虑了压敏效应对油井生产能力的影响。为了验证压敏效应对稠油油藏的具体影响，分别从累积产油量以及含水率2 个生产指标来验证。

考虑压敏效应会直接导致区块的早期含水率升高并且累积产油量降低，其原因在于考虑压敏效应会引起生产井井底的压力降低更快，间接导致渗透率下降幅度变大，从而引起井的传导阻力增大，导致开发效果变差［27］（图9）。

图9 应力敏感对生产指标的影响Fig.9 Influence of pressure sensitivity on production index

4 模拟器的应用与分析

由于目标区块属于典型的稠油油藏，因此仍使用ECLIPSE 软件来匹配整个区域的采油速度和含水率，而无需考虑稠油油藏的非线性渗流。根据采油速度和含水率的历史拟合效果可以看出，忽略启动压力梯度与压敏效应的存在，将对稠油生产指数产生重大影响，而拟合效果不如预期。

基于稠油油藏渗流机理和矿场试验，将自行研发的模拟器和新增的注水稠油关键词用于历史匹配。加入非线性渗流关键字并且考虑压敏效应后，开发曲线的拟合效果明显提高，这为客观地研究稠油油藏渗流场变化规律及优化调整提供了重要的指导作用（图10）。

图10 Y3区块含水率和日产油量拟合曲线对比Fig.10 Comparison of fitting curves of water cuts and oil production rates in Y3 block

通过引入有效驱替压力梯度（驱替压力梯度减去启动压力梯度）的概念，用数值模拟方法输出目标层位的有效驱替压力梯度场（图11）。当有效驱替压力梯度大于0，该网格的流体方可有效驱替，灰色区域代表有效驱替压力梯度小于0，即原油未得到有效驱动。该场图可以初步定位稠油油藏区块的弱驱替区，即当前时间步稠油油藏的滞留区，为剩余油的挖潜工作提供依据。

图11 油组有效驱替压力梯度场Fig.11 Effective displacement pressure gradient field of oil formations

5 结论

在实验基础上提出了基于应力敏感的稠油油藏变启动压力梯度模型，并且通过自研模拟器的编制及测试，得出无论是机理模型还是矿场实际模型，计算结果与ECLIPSE 基本一致。模拟器非线性模型以及压敏效应的测试结果也表明，启动压力梯度会加快最小渗流阻力通道的形成，减小水驱波及面积，加剧水相的指进现象；压敏效应会导致含水率快速上升，驱油效率大幅降低。将自研模拟器应用于矿场实际模型，可以客观地描述稠油油藏的非线性渗流情况，显著提高了历史拟合的准确性以及对油井生产指数的预测能力，模拟结果更加符合实际；同时模拟器输出的有效驱替压力梯度场为后续的稠油油藏开采提供了技术支持。

符号解释

a，b——渗流实验拟合参数；

A——网格面积，m2；

Bl——体积系数；

D——油藏埋深，km；

f——油相流动修正系数；

Fo——油相势梯度模大于启动压力时的修正系数；

g——重力加速度，m/s2；

G——启动压力梯度，MPa/m；

l——取o，w，g，分别代表油相、水相、气相；

L——网格x，y，z3个方向的长度，m；

k——迭代次数；

K——油藏的绝对渗透率，mD；

Ko——油相有效渗透率，mD；

Krl——油、气、水相相对渗透率；

m——时间步；

n——油藏外边界Γ的法线方向；

p——地层压力，MPa；

Δp——地层压力分别与油、气、水相压力的差值，MPa；

pl——油、气、水相压力，MPa；

pcow——油、水两相间的毛管压力，MPa；

pcog——油、气两相间的毛管压力，MPa；

p0(x,y,z)——初始条件下的原始地层压力分布，MPa；

qvo，qvg，qvw——标况下油、气、水相流体在单位时间下单位体积岩石中流入或采出的体积，m3/s；

Qvg——标况下气相流体在单位时间下网格块中流入或采出的体积，m3/s；

Qvo——标况下油相流体在单位时间下网格块中流入或采出的体积，m3/s；

Qvw——标况下水相流体在单位时间下网格块中流入或采出的体积，m3/s；

Rso，Rsw——溶解气在油相和水相的溶解气油比；

Sl——油、气、水相饱和度；

t——时间，s；

Tl——油、气、水相传导率，mD∙m；

vo，vg，vw——油、气、水相流体的渗流速度，m/s；

Vb——网格块的体积，m3；

x,y,z——地层坐标；

xw,yw,zw——井点坐标；

Γ——油藏外边界；

——m+1 时间步po，Sw等参数第k+1 次与第k次迭代的差值；

μl——油、气、水相黏度，mPa∙s；

μoa——油相视黏度，mPa∙s；

ρo，ρg，ρw——油、气、水相流体的密度，kg/m3；

φ——孔隙度；

Φo，Φg，Φw——油、气、水相流体的流动势，MPa。