基于多维度低位路灯的结构分析及优化

张 兵，崔朋杰，赵海天

(深圳大学，广东 深圳 518060)

引言

道路照明的作用在于夜间为驾驶员提供适宜的光环境，保证驾驶员的环境辨别能力与视觉舒适度。人体对于外界信息的接收80%以上都是通过视觉获得，所以驾驶员对于道路照明的路面亮度有着较高的要求[1]，而高标准的亮度要求则意味着大量的电力消耗，目前我国各类路灯有3000万盏以上，并且还在以每年约6.75%的速度增加，经统计道路照明每年的耗电量约占全社会耗电总量的3%，并且此比例还在持续上升。为了降低照明能耗，人们从光源、光学配光[2]、智能控制[3]、照明方式[4]以及视觉上[5]进行了研究。从节能优化空间上来看光源优化[6]、光学配光与智能控制短时间内不会有太大突破，而道路照明方式与视觉亮度的研究目前还不够充分。

本文的研究基于多维度照明体系，涉及到一种新的照明方式，多维度低位路灯的优势在于根据驾驶员的视觉需求设计了正逆向的低位照明方式，提高了路灯的照明效率，在武汉市青山大桥五车道20 m路宽的测试实验中使用亮度成像计对光度数据进行了测试，在能耗低于国家标准47%的情况下，亮度达到了国家标准3倍[7]，测试数据与国家标准对比如表1所示。但实验路面为水泥混凝土路面，亮度较柏油路面偏高，实际柏油路面的应用中亮度应为3～4 cd/m2，意味着在实际应用中功率密度可以降低至0.275 W/m2。

虽然此照明方式相比传统路灯可以极大地降低能耗，但多维度低位路灯为了提升路面亮度均匀度、消除眩光，灯具本身仍存在着出光效率较低的问题，经过测试其出光效率约为15%，经全空间分布式光度计测试后整灯能效仅为23.28 lm/W。这意味着如果可以从根本上提高灯具出光效率，那么道路照明的能耗可以降低至国家标准的1/10以下。

表1 多维度低位路灯与国家标准参数对比

1 多维度照明体系分析

1.1 道路照明效率模型分析

路灯的照明效率实际上是指经过路面反射射向驾驶员方向的光线与灯具发出的光线总数的比值，即路面反射效率，其涉及到了观察者的位置、观察者观察的位置、观察点的光线入射角度以及路面反射情况[8]。

在道路照明模型中，可以认为驾驶员的位置与观察点的位置是相对不变的，即视轴方向φ角(观察角)不变，而路面状况也是恒定的，则影响路面反射效率的唯一变量为光线入射角度。作为机动车驾驶员的观察者，其观察高度通常距离路面1.2～1.6 m；与观察点的距离为60～160 m；观察角φ的取值为0.5°～1.5°[9]，本文观察角取中间值为φ=1°。在道路照明中应以Er·e的分量作为路灯有效辐射效率的衡量标准，如图1所示。

图1 有效照明与无效照明分量分析图Fig.1 Analytical diagram of effective lighting and ineffective lighting components

图中Er为光源在路面上的反射照度矢量；Er·e为路面反射照度在驾驶员视轴方向的分量；α为光源的入射角，即路面法线与光源投光方向之间的夹角；φ为机动车驾驶员视线方向与路面之间的夹角，取φ=1°；θ为光源投光方向所在平面与驾驶员视线方向所在平面的夹角。

当路灯位于道路两侧，路面规则反射且不计光线空气传输中的能量损失时，竖向反射分量表达式为

Er·v=Er·cosα

(1)

横向反射分量表达式为

Er·t=Er·sin(α+φ)·sinθ

(2)

光源在驾驶员视轴方向的照度分量为视网膜分量，可表达为

Er·e=Er·sin(α+φ)·cosθ

(3)

根据前文关于路面反射效率的分析，可知对于驾驶员来讲Er·e是驾驶员分辨障碍物和观察路面的有效辐射分量[10]，而Er·v和Er·t则分别射向天空与路旁，属于无效分量，这一结果说明了现有高杆灯与低位路灯高能耗的原因[11]。

根据以上分析，当路面粗糙度较低的时候，应该将光源置于低位并采用逆向照射，如图 2所示，并使光源垂直角可以趋近于1°，这时道路照明模型中Er·e分量可取得最大值；在粗糙道路上则照明方向与驶员视线方向相同,即采用正向照明，如图 3所示。但在当前的应用中无法判断对于低位道路照明来讲路面是粗糙还是光滑，并且柏油路面还会经历一个从粗糙到光滑的过程，所以采用了正逆向结合的照明方式。

图2 正向照明Fig.2 Forward lighting

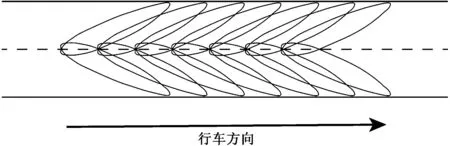
图3 逆向照明Fig.3 Reverse lighting

1.2 光学配光分析

正逆向的照明理论要求路灯的照射方向与道路方向相反或相同，而低位路灯安装于道路两侧1 m高度以下，这就要求出光必须与路边存在一水平角将光线投射到路中央，如图 2、图 3所示，而这个水平角越小则意味着照明效率越高，所以需要增加路灯的距高比，增加照射距离。本文中的距高比是指光斑最亮点与灯具的距离和灯具安装高度的比值，低位路灯高度较低，所以为了保证路面亮度均匀性就必须提升距高比。

多维度路灯为了提升距高比采用了大尺寸的TIR透镜(全内反射透镜)[12]，可以将LED光源发出的朗伯体分布的光线转化为近似准直的出光，让光线射得更远，为了增加光斑的覆盖面积在透镜出光面设计了波纹镜将准直出光横向扩散，既提升了距高比，又增加了照明范围，如图4所示。经过分布式光度计测试得到透镜出光水平方向配光角约为7.5°，竖直方向配光角约为5.7°。

图4 TIR透镜剖面结构示意图Fig.4 Schematic diagram of TIR lens cross-sectional structure

1.3 结构配光分析

多维度路灯简化结构如图 5所示，灯具结构主要由TIR透镜和截光板两个部分组成。透镜作用是将LED光源的朗伯体出光转化为近似准直出光并将其投射到地面上，根据驾驶员在行驶过程中的视野范围可以确定驾驶员视线在0.5°～1.5°之间，所以此灯具设置垂直角为1°。由于透镜出光面为准直出光，所以有很高的能量密度，在正逆向的照明方式下出光面会不可避免地进入驾驶员的视野造成非常强烈的眩光。为了消除眩光便加入了截光板，低位路灯的发光面高度位于驾驶员眼睛(1.2 m)以下，所以截光板的作用是将透镜出光面发出的水平以上可以进入驾驶员眼睛的光线遮挡，如图5所示，保证灯具的出光只能为路面提供照明。结构中为了保证完全消除眩光，要求透镜出光面的底部要与截光板的底部平齐，这就使得整个灯具的出光效率很低。

观察图 5，假设透镜出光完全准直，则透镜出光面在竖直方向上只有一定高度h的光线可以射出，若透镜垂直角为θ，透镜出光面与截光板距离为d，则有效出光面高度h的表达式为：

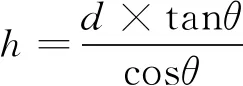
(4)

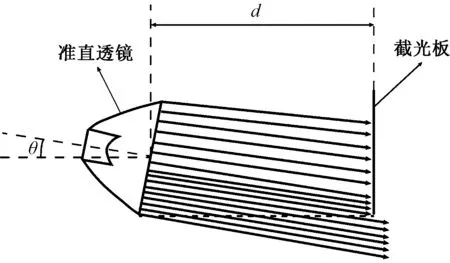
图5 多维度低位路灯简化图Fig.5 Simplified diagram of multi-dimensional low-level street lights

假设θ=1°，d=350 mm，计算可得h≈6.1 mm，此值远小于透镜的直径70 mm。但实际上的透镜出光为近似准直，所以实际上的h值大于6.1 mm，但可以确定h值一定是远小于70 mm，可以得出优化的途径为降低透镜的出光面高度。

2 灯具出光效率优化实验

切割透镜使H变为h，此做法与上述结构相似，不同之处在于需要在H中选择某一部分h，由于透镜出光面的能量分布是非均匀的，所以在透镜出光面上必然可以选择出一个h得到最大的出光效率，这种方式是目前多维度路灯使用的方式。

2.1 透镜出光面能量分析

透镜出光表面的能量密度曲线无法测量，所以由软件模拟获得，模拟思路为将透镜在竖直方向上分割为数十个宽度为2 mm的部分，再对其能量值一一测量得出光通量数据，然后计算每一部分的面积，最后相除得到每一部分的能量密度，最后画出能量密度曲线。

2.1.1 透镜出光面能量分析

透镜出光表面的能量分布曲线无法通过仪器测量，所以需要通过软件模拟获得，将透镜出光面在竖直方向上进行分割，每一部分高度为2 mm，然后以每一部分为出光口，其余部分遮挡，测试每2 mm的出光光通量。将获得的数据制成分布曲线如图6所示。

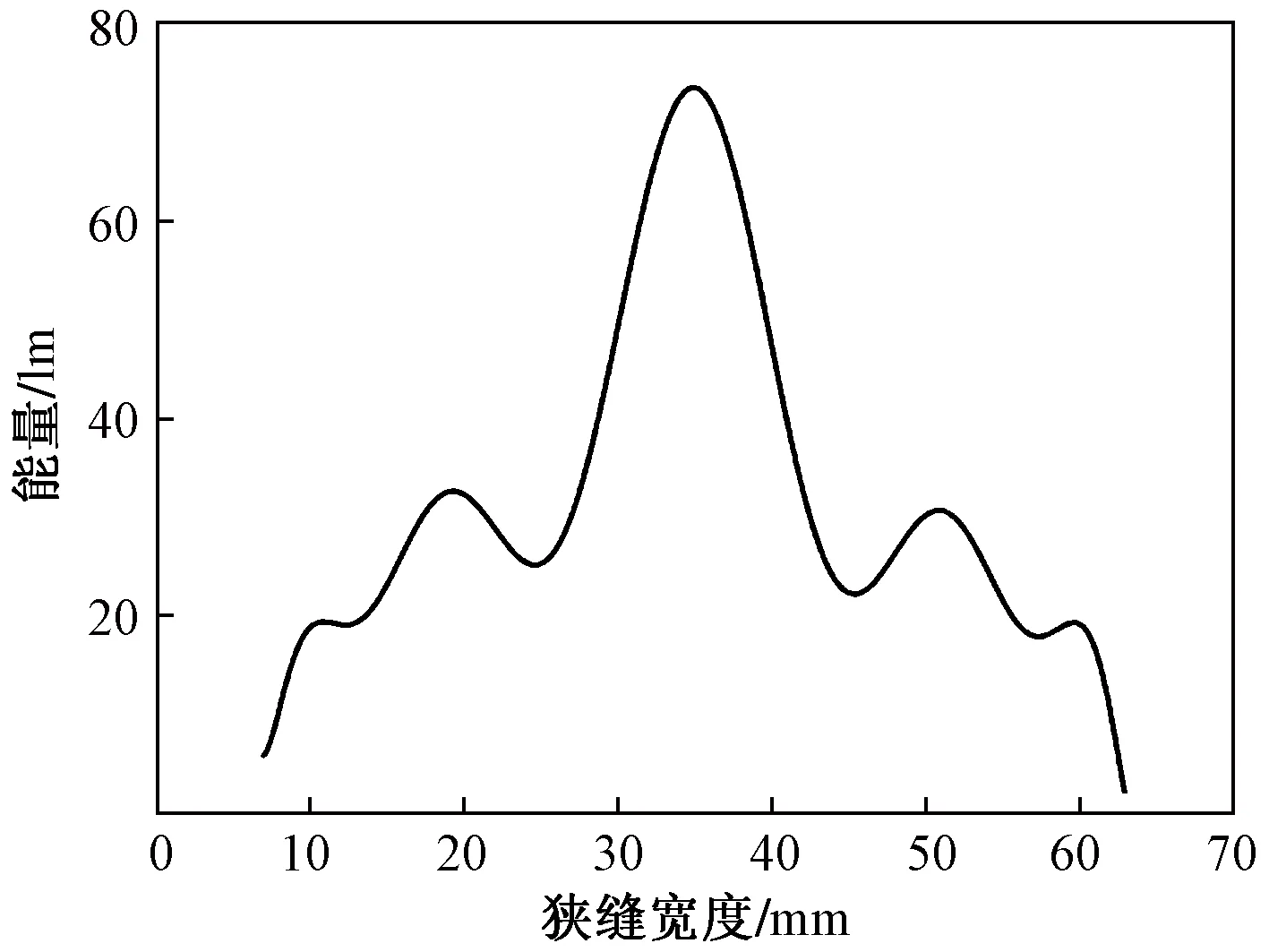
图6 透镜出光面竖直方向能量分布图Fig.6 Vertical energy distribution diagram of the light-emitting surface of the lens

2.1.2 能量密度分布

实验中所采用TIR透镜的出光面直径为70 mm，实际使用的透镜区域长度为56 mm，如图7所示。

图7 透镜面积计算示意图Fig.7 Schematic diagram of lens area calculation

沿透镜56 mm长的方向将出光面等长分割，透镜不同位置的面积满足公式：

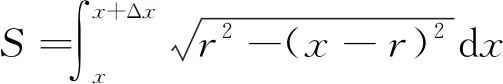
(5)

实验中，r=35 mm，x∈[7，63]， Δx=2 mm，将模拟所得各个位置光通量除以对应面积，得到透镜的能量密度分布。将得到的能量密度数据进行曲线插值和拟合，得到出光面竖直方向的能量密度曲线，如图 8所示，由图8可知透镜出光面的大部分能量集中在透镜中部25～45 mm，宽度约为20 mm的区域，若要在现有结构下提升出光效率，则需要得出具体透镜出光高度，然后选取出光面中部相应高度作为出光面。

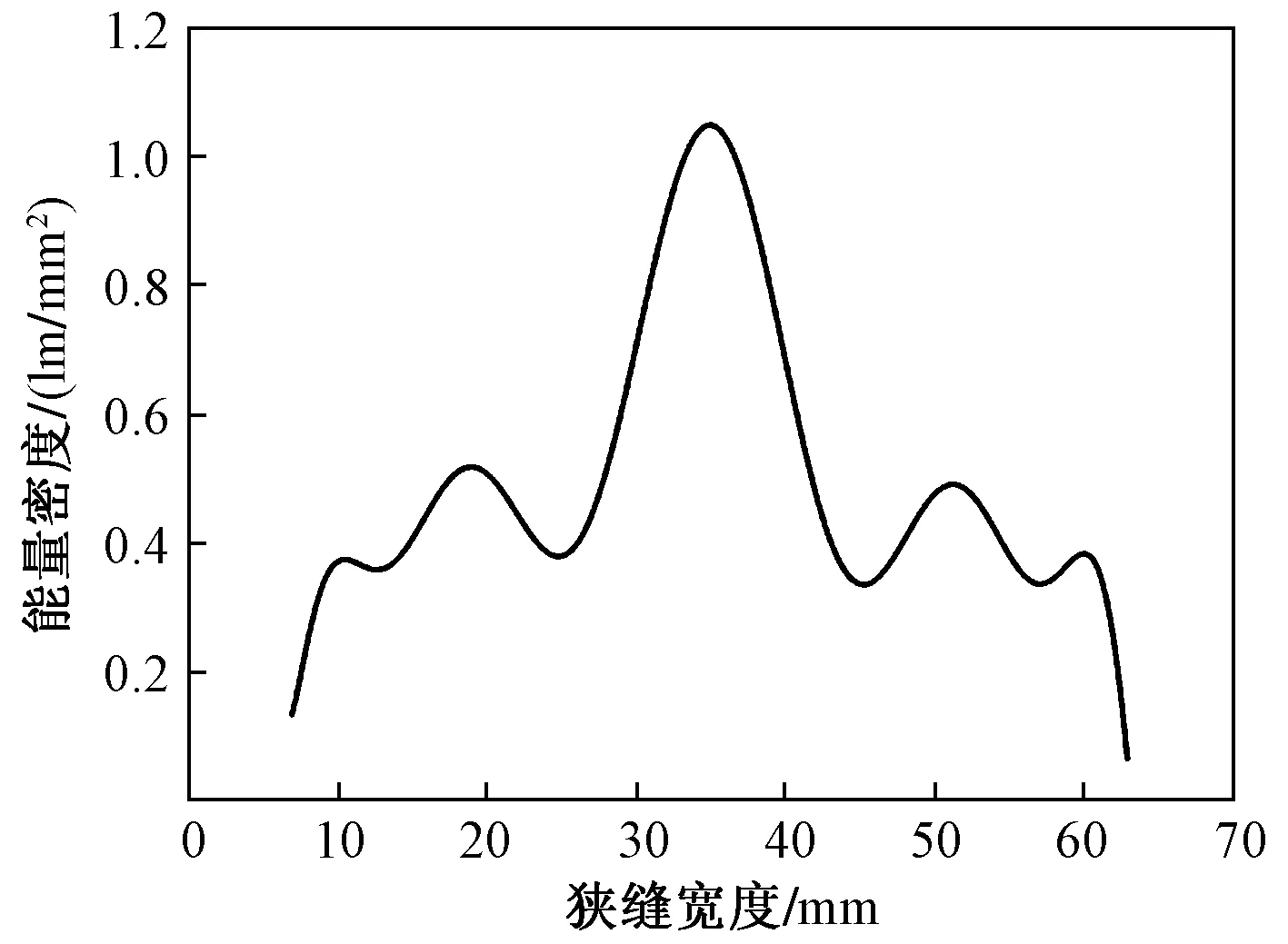
图8 能量密度曲线Fig.8 Energy density curve

2.2 透镜出光高度测试实验

根据灯具的结构分析可知透镜出光面只有一部分高度的光线可以照射到地面，所以需要模拟实验获得此出光高度，模拟步骤是将透镜出光面的有效出光高度h分别设置为2 mm、4 mm、6 mm……，出光高度h以外的出光面设置遮光板遮挡，如图9所示。然后进行光线追迹获得不同狭缝宽度的能量利用效率，能量利用效率会随着狭缝宽度h值的增大而增大，而在h增大到某一值时，总能量值停止增加，此时便为出光面的有效出光高度，测得数据如表2所示，制成二者关系图如图10所示。

图9 出光高度测试示意图Fig.9 Schematic diagram of light emission height test

表2 灯具出光光通量与出光高度关系

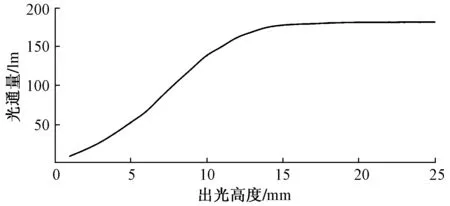
图10 灯具出光光通量与出光高度关系图Fig.10 The relationship between the luminous flux and the height of the luminaire

由表2可知，狭缝宽度在24 mm之后能量的使用效率便不再增加，这表明透镜的折射部分的极限狭缝宽度为24 mm；但观察图10可知光通量在15 mm之后几乎就没有增加，因此可以以15 mm作为此结构的有效出光高度。在透镜出光面能量分布图中找到能量分布最多的15 mm，即27.5～42.5 mm,再次进行软件模拟，结果表明灯具出光效率提升至为19%，相比原灯具的15%提升了27%。

3 透镜优化设计

3.1 设计思路

根据优化目标改变透镜形态，设计透镜出光口趋于长方形，即减小垂直方向的尺寸，增大水平方向的尺寸。由于设计存在一定的复杂性，垂直方向高度受到限制，所以透镜出光面初始目标尺寸设定为20 mm×80 mm。

设计采用了不同直径的TIR透镜拼接的形式，首先先设计直径分别为20、30、40、50、60、70、80 mm的透镜，然后将直径20 mm的透镜切割为55°，将直径30～70 mm的透镜切割为10°，将直径为80 mm的透镜切割为25°，最终将所有透镜进行拼合，得到的模型如图11所示，此模型出光口高度为20 mm，宽度为80 mm。

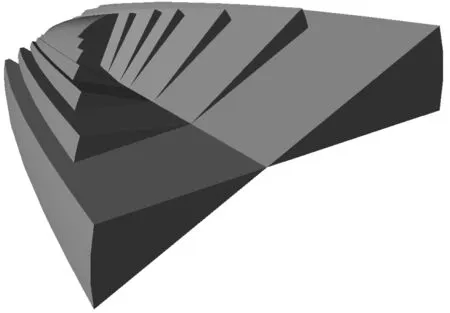
图11 异形透镜模型图Fig.11 Special-shaped lens model diagram

3.2 软件模拟对比分析

将异形透镜替换原TIR透镜进行光线追迹，得到照度图显示灯具的出光效率达到了约32%。相比原灯具效率提升了113%。

为了验证异形透镜的均匀性，使用软件Tracepro导出灯具的ies文件，然后将文件导入软件DIALux进行路段模拟。路面宽度为20 m，布灯方式与武汉市青山大桥测试相同，为双侧布灯，路灯间距3 m，高度为0.85 m，单灯功率为16 W。原灯具模拟结果如图12所示，异形透镜灯具模拟结果如图13所示。对于多维度低位照明，由于亮度计算公式中所涉及到的简化亮度系数与高位路灯完全不同，软件无法给出较为准确的亮度参数，因此采用了照度参数，各项照明参数如表3所示。

图12 原始灯具路段模拟图Fig.12 Simulated map of the original lighting section

图13 异形透镜灯具路段模拟图Fig.13 Simulated map of special-shaped lens lamp road section

表3 优化前后照明参数对比

观察图12与图13可知，路面纵向均匀度极高，但可以明显看到异形透镜的路段中间照度高于原始灯具，即横向均匀度与总均匀度优于原灯具。观察表3可知，灯具优化后在相同的功率密度下平均照度值提升了127%，总照度均匀度提升了约55.6%，因此可以认为异性透镜的出光效率与照明质量均有所提升。

4 结论

1)通过对多维度照明体系的照明方式进行分析得到了多维度照明体系相比传统路灯节能的原因，在于其从驾驶员视觉角度设计了灯具光束的照射方向，正向与逆向的照明方式极大的增加了驾驶员视角的路面反射效率。

2)通过对多维度低位路灯的光学配光和结构配光进行分析，指出了此照明方式高均匀性的原因在于采用了大直径的TIR透镜增大路灯距高比。但同时TIR透镜结合截光板造成了灯具出光效率极低，初始出光高度仅为15%，分析得到影响灯具出光效率的因素是透镜出光面高度。

3)透镜出光高度测试得到透镜出光面大约只有15 mm的出光高度，根据实验测试得到透镜出光面能量分布中间高两侧低，所以选取透镜中部15 mm作为出光面，最终将灯具出光效率提升至19%，相比原结构提升了27%。

4)分析得到增加灯具出光效率的途径为降低透镜出光面高度，所以设计了出光口约为20 mm×80 mm的异形透镜进行试验，实验结果表明异形透镜将灯具出光效率提升至32%，相比原结构提升了113%。