基于3×3相位解调的光纤地震检波器研究

刘 超，周 瑜，张健博，张乐意，王坤博，李 勤

（中国电子科技集团公司第三研究所，北京 100015）

0 引言

当前，地震勘探技术是地球物理勘探最重要的方法，主要是通过记录由人工震动引起的、经过岩层分界面反射或折射的地震信号，达到认识地下地质构造的目的，实现地质勘探，已被广泛应用于石油、天然气及金属矿等勘探领域[1]。地震检波器作为地震勘探系统的核心部件，其性能直接决定了地震勘探系统的成像效果，影响地震勘探系统的勘探性能。目前，地震勘探领域逐步向复杂地表条件和地下复杂区域发展，对地震检波器也提出更高的要求[2-4]。作为当前地震勘探系统中使用最广泛的地震检波器，动圈式地震检波器灵敏度低、有效带宽相对较窄、抗电磁干扰能力差，已无法满足地震勘探系统高精度成像的需求，尤其是深地地 质的需求[5]。

光纤地震检波器以光纤为媒质、以光为载体，感知和传输地震波信号，具有灵敏度高、体小质轻、前端无源、抗电磁干扰、便于组网成阵以及易长距离传输等优点[1，6]，受到了国内外研究者的广泛关注。2002年，日本海洋科技中心和OKI电子公司提出了用于探测海底地震波的干涉式光纤地震检波器，最小分辨率为30 ng/@10Hz，可实现三维方向的地震波信号的测量[7]。2004年，胜利油田物探公司与斯蒂文斯理工学院共同开发了一种光纤光栅地震检波器，进行了陆上野外采集试验[8]。2004年，清华大学的ZENG N等人设计了一种用于测井地震观测的三分量干涉型光纤地震检波器，采用推挽式结构，能够实现灵敏度为89.1 rad/g、工作频率为3～800 Hz的地震波信号探测[9]。2007年，日本NIT公司用于海底地震和海啸预警的光纤光栅地震检波器，灵敏度高达600～1000 pm/g，放置在日本伊豆半岛离海岸4 km深的海底，能够实现对日本东海、东南海及南海的海底地震监测[10]。2013年，中科院半导体所张文涛等人提出了一种基于悬臂梁的推挽式三分量光纤地震检波器，其灵敏度为 45 dB（0 dB=1 rad/g），工作频率为10～450 Hz[11]。2016年，中国科学院声学研究所与中国电子科技集团公司第二十三研究所提出了适用于陆地油气勘探的16通道光纤地震检波器采集系统，系统所采用的光纤地震检波器的灵敏度为40 dB（0 dB= 1 rad/g），工作频率为10～800 Hz[12]。2020年，北京大学张敏等人提出了专门针对井下微地震监测的光纤传感系统，所采用的光纤地震检波器的灵敏度为200 rad/g，工作频率为10～1000 Hz[13]。

本文将研究基于3×3相位解调的光纤地震检波器，采用基于最小二乘法的椭圆拟合法和微分交叉相乘处理（DCM）算法，实现了基于3×3相位解调的光纤地震检波器的两路输出信号的归一化以及外界振动信号的准确还原。实验通过对比法测试了基于3×3相位解调的光纤地震检波器的性能，其灵敏度为320 rad/g @100 Hz，在5～400 Hz频率范围内的波动约为0.7 dB。

1 工作原理

基于3×3相位解调的光纤地震检波器如图1所示，主要包含窄线宽激光器、光纤地震检波器、光电探测器、采集卡以及电脑。窄线宽激光器发出一束单波长的光束，通过光纤地震检波器的输入光纤进入光纤地震检波器，进行振动测量；经过光纤地震检波器的两根输出光纤，将加载有振动信息的光信号传输至光电探测器进行光电转换，形成相应的电信号，由采集卡采集处理，解调出原始振动信号，从而实现地震振动信号的准确还原。

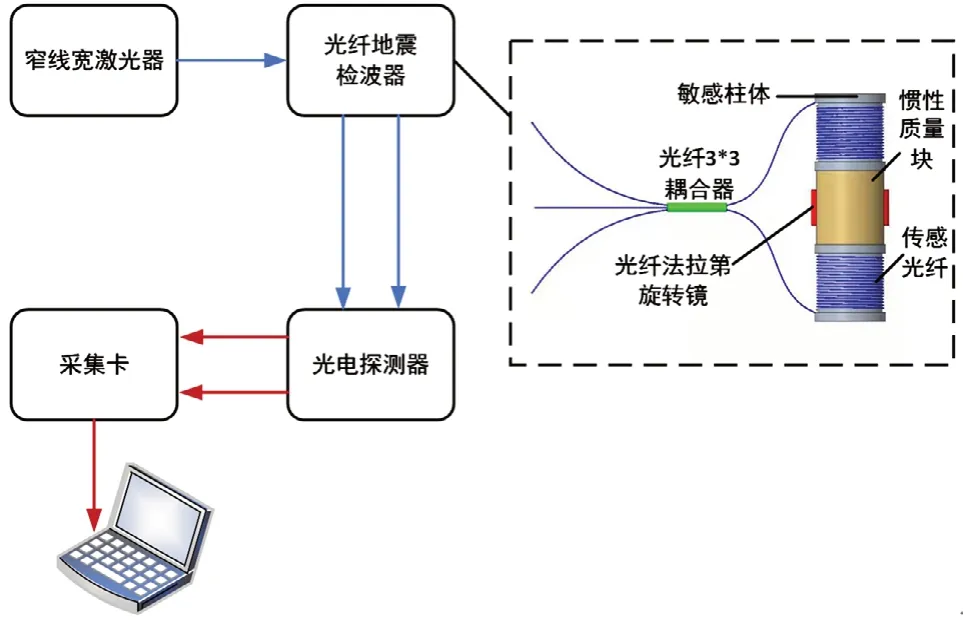
图1 基于3×3相位解调的光纤地震检波器的工作原理 示意图

光纤地震检波器为基于光纤迈克尔干涉的推挽式地震检波器，主要由光纤3×3耦合器、传感光纤、光纤法拉第旋转镜、敏感圆柱以及惯性质量块组成。惯性质量块位于两个敏感圆柱中间，形成推挽式结构；传感光纤缠绕在敏感圆柱上，与光纤3×3耦合器和光纤法拉第旋转镜形成光纤迈克尔逊干涉结构。当光纤地震检波器接收到地震的振动信号，振动信号将促使惯性质量块发生相对的谐振运动，挤压或者拉伸敏感圆柱，从而使缠绕在敏感圆柱上的传感光纤的长度发生相应的变化，引起光纤迈克尔逊干涉结构的相位发生改变。通过相位解调，就能够将地震的振动信号准确还原，实现地震振动信号的测量。

对于基于光纤3×3耦合器的光纤迈克尔逊干涉结构而言，其两根输出光纤的输出光强[14]分 别为：

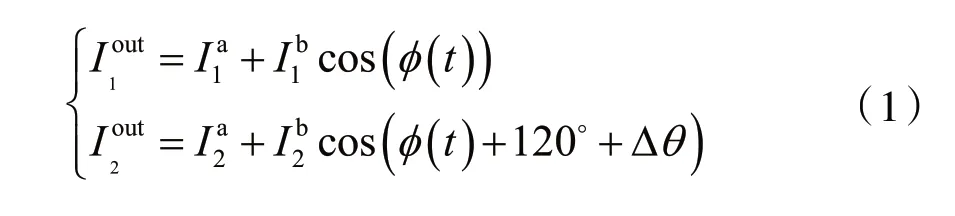
经过光电探测器的光电转换后，式（1）转变为：

从式（2）可以看出，两路输出信号V1和V2都是由振动信号函数φ(t)进行调制，满足李萨如图的形成条件，可由椭圆方程[15-16]表示为：

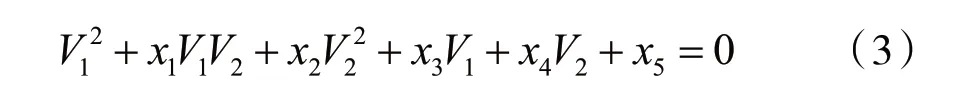
椭圆系数x1、x2、x3、x4、x5与输出信号的直流项系数和交流项系数之间的关系为：

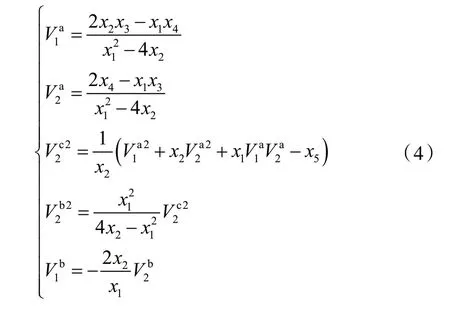
因此，通过求解椭圆系数x1、x2、x3、x4、x5即可得到两路输出信号的直流项和交流项系数，从而能够将两路输出信号实现归一化，可表示为：

对于椭圆系数x1、x2、x3、x4、x5的求解主要通过将采集到的两路输出信号的数据进行椭圆拟合的方法得到。最小二乘法作为椭圆拟合中基本和有效的方法之一，能够快速地求解出椭圆系数，其原理是根据实测的数据求解出一组最优解的椭圆系数，使得实测数据到拟合出的结果曲线间的距离之和最小；在基于代数距离的最小二乘法中，这距离为椭圆方程式（3）从采集数据点到期望值0之间的残差。令残差平方和最小，则椭圆系数x1、x2、x3、x4、x5需满足偏微分方程组[15]：

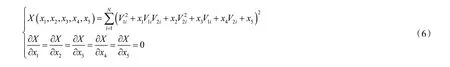
式中：N为用于拟合的输出信号的数据的数量。

由于直接最小二乘法的拟合结果容易退化成双曲线，因此，为了保证拟合结果的准确性，需引入约束条件4x2-x12=1，使得式（6）能够有唯一最优解。因此，式（6）可表现[17]为：

式中：x=[1,x1,x2,x3,x4,x5]T是椭圆系数向量；M和S分别是所采集数据矩阵和中间矩阵，

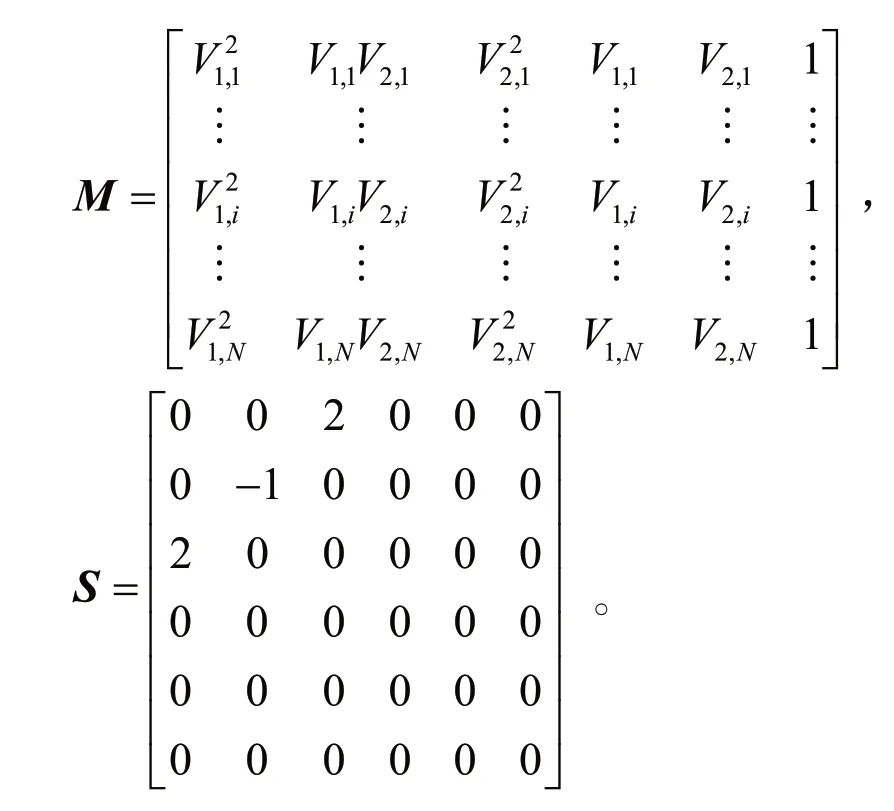
利用拉格朗日乘数法，式（7）可表征为：

式中：D=STS，λ为拉格朗日因子。

通过求解广义特征向量的方法，可从式（8）得出椭圆系数x1、x2、x3、x4、x5，进一步得到两路输出信号的直流项和交流项系数实现两路输出信号的归一化。

实现两路输出信号的归一化后，地震的振动信号可利用DCM算法实现准确还原。DCM算法的解调过程如图2所示，主要包含微分、交叉相乘、相减以及积分滤波过程[18-19]。

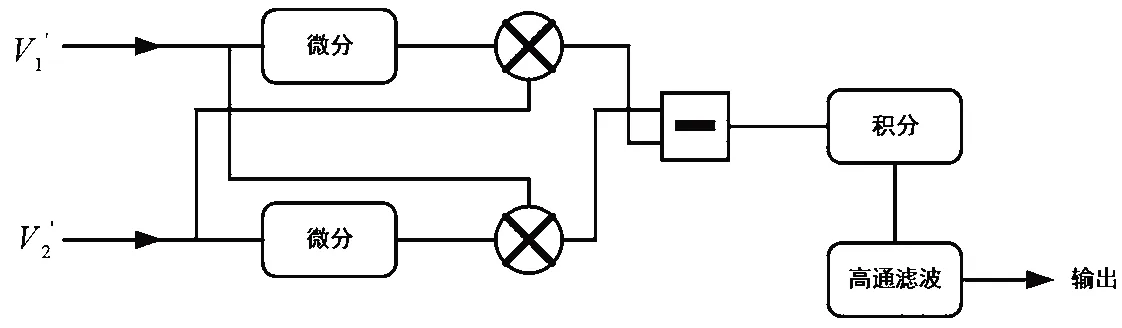
图2 DCM算法解调过程示意图

归一化后的两路输出信号经过微分后，两路输出信号分别为-sin(φ(t))φ'(t)和cos(φ(t))φ'(t)，微分后的信号与微分后的信号交叉相乘后，分别能够得到-sin2(φ(t))φ'(t)和cos2(φ(t))φ'(t)，相减后为φ'(t)，积分后就能够得到振动信号φ(t)；高通滤波能够将初始相位和温度等外界干扰滤除。

2 实验研究

在实验中，基于3×3相位解调的光纤地震检波器采用对比法进行测试。基于3×3相位解调的光纤地震检波器测试系统如图3所示，主要由窄线宽激光器、光纤地震检波器、光电探测器、采集卡、标准加速度传感器、驱动电路、信号发生器、功率放大器以及振动台组成。其中，振动台为BK 4808，功率放大器为BK 2719，标准加速度传感器为理音压电式加速度传感器PV-87，驱动电路模块为理音VP-40，窄线宽激光器为RIO窄线宽激光器，采集卡为NI 6366。信号发生器发出单频的正弦信号，通过功率放大器进行放大，驱动振动台发生相应的振动，从而引起同轴安装的光纤地震检波器和标准加速度传感器的振动。窄线宽激光器发出单波长的光束，通过光纤地震检波器的输入光纤进入安装至振动台上的光纤地震检波器，由光纤地震检波器的两根输出光纤传输至光电探测器进行光电转换，将光信号转换成电信号，由采集卡进行采集，从而能够进行相位解调，准确还原出振动信号。标准加速度传感器由驱动电路模块进行驱动，其输出电信号由采集卡采集。通过对比光纤地震检波器的解调信号与标准加速度传感器的输出信号，实现基于3×3相位解调的光纤地震检波器性能测试。不同振动信号频率下的基于3×3相位解调的光纤地震检波器的测试结果如图4所示。

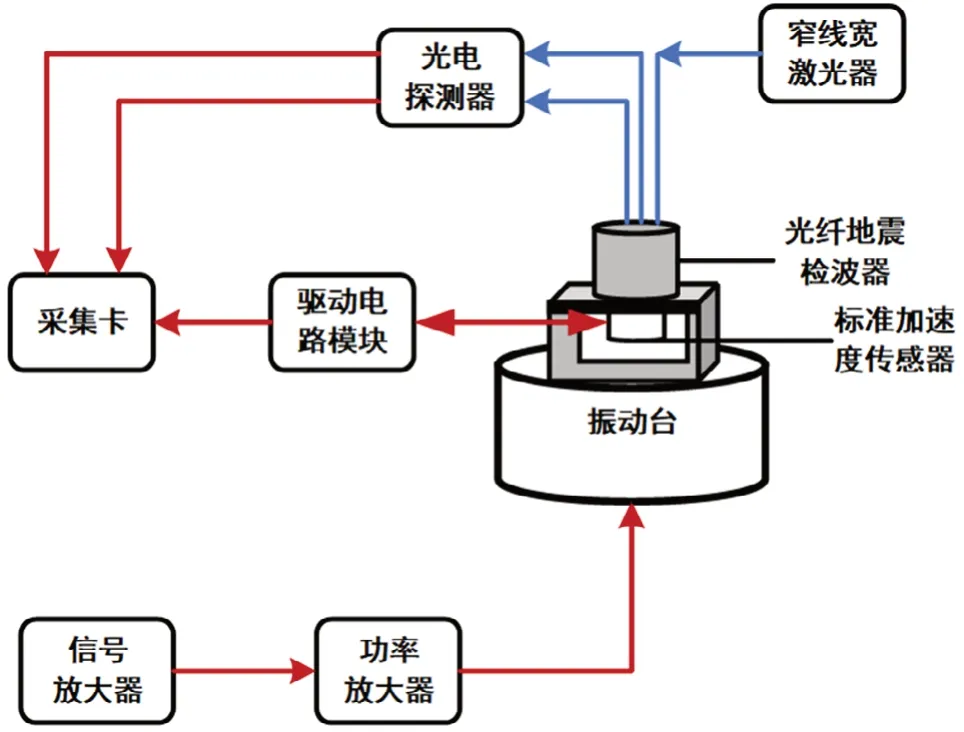
图3 基于3×3相位解调的光纤地震检波器测试系统示意图

从图4可以看出，基于3×3相位解调的光纤地震检波器能够准确地还原振动信号，且灵敏度远远高于标准加速度传感器。当振动频率为100 Hz时，基于3×3相位解调的光纤地震检波器的灵敏度为320 rad/g。

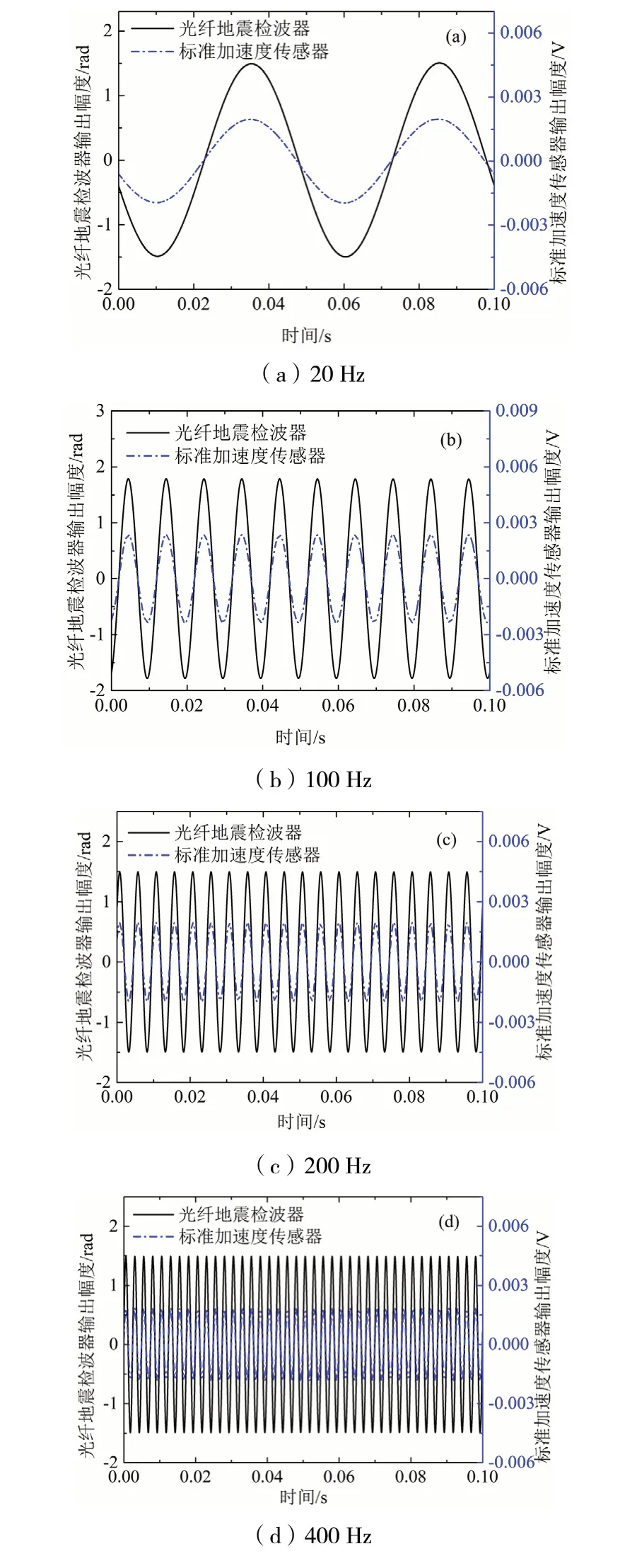
图4 不同振动信号频率下的测试结果

基于3×3相位解调的光纤地震检波器的频率响应特性如图5所示。从图5可以看出，基于3×3相位解调的光纤地震检波器具有较为平坦的频率响应特性。在5～400 Hz频率范围内，基于3×3相位解调的光纤地震检波器的频率响应波动约为0.7 dB。

图5 基于3×3相位解调的光纤地震检波器的频率响应特性

3 结语

本文针对基于3×3相位解调的光纤地震检波器展开研究，采用基于最小二乘法的椭圆拟合法实现了基于3×3相位解调的光纤地震检波器的两路输出信号的归一化，减小了光纤3×3耦合器的非对称性和激光器的功率波动对光纤地震检波器的影响；采用DCM算法实现了光纤地震检波器的相位解调，准确还原了振动信号。实验通过对比法测试了基于3×3相位解调的光纤地震检波器的性能，其灵敏度为320 rad/g @100 Hz，在5～400 Hz频率范围内的波动约为0.7 dB。本文的研究能够很好地应用于石油和天然气等的地质勘探、地震监测以及周界安防等领域。