一种改进的贝叶斯小波阈值图像去噪算法
余传本,刘增力
(昆明理工大学 信息工程与自动化学院,云南 昆明 650500)
0 引言
图像去噪是图像处理的经典问题。在图像获取或传输的过程中,由于各种因素的干扰,图像通常会不可避免地被噪声污染。因此在对图像执行后续处理之前,必须先对图像进行去噪处理。常用的降噪方法有维纳滤波、中值滤波等[1-2],但是这些方法在对图像进行降噪的同时,也会丢失图像的部分细节。而小波去噪方法在一定程度上克服了上述缺点,可以在去除噪声的同时保持图像的细节 部分[3]。
长期以来,国内外的相关学者对小波去噪进行了众多研究,包括使用小波系数相关去噪、小波阈值去噪、模极大值去噪等。从最小均方误差的角度来看,小波阈值去噪方法在获得较好视觉效果的前提下,基本上可以达到最佳的去噪效果[4]。常用的阈值确定方法[5-7]有VisuShrink、SureShrink、BayesShrink以及Feature Adaptive等。
本文在贝叶斯收缩去噪方法的基础上提出了一种改进的方法,即自适应贝叶斯阈值方法。在原始方法中,每个小波子带只有一个阈值。改进的方法基于区域划分为每个小波系数计算模糊小波系数,并获得每个系数的阈值。实验结果表明,与原始方法相比,该方法在信噪比和均方差等客观指标和主观视觉效果方面均有显著改善,并且可以更好地保持图像边缘细节。
1 小波阈值图像去噪原理
1.1 图像的小波分解
通过小波变换将图像分解为各种子带的方法有很多,如小波包分解、八带分解、均匀分解以及非均匀分解等。其中,八带分解是最常用的一种分解方法,原理如下:使用低通滤波器h和高通滤波器g对图像的行和列进行滤波(卷积),然后对其中的两个进行降采样。这样,小波变换的结果会将图像分解为低频子带(水平和垂直方向均经过低通滤波)LL和三个高频子带,即用HL表示水平高通、垂直低通子带,用LH表示水平低通、垂直高通子带,用HH表示水平高通、垂直高通子带。分辨率是原始分辨率的1/2,并且频率范围也不同。第二次小波变换时只对LL子带进行,进一步将LL子带分解为LL1,LH1,HL1和HH1,并且分辨率是原始子带的1/4,频率范围进一步减半,依此类推。因此,如图1所示,执行一次小波变换可获得4个子带,进行M次分解可获得3个M+1子带。
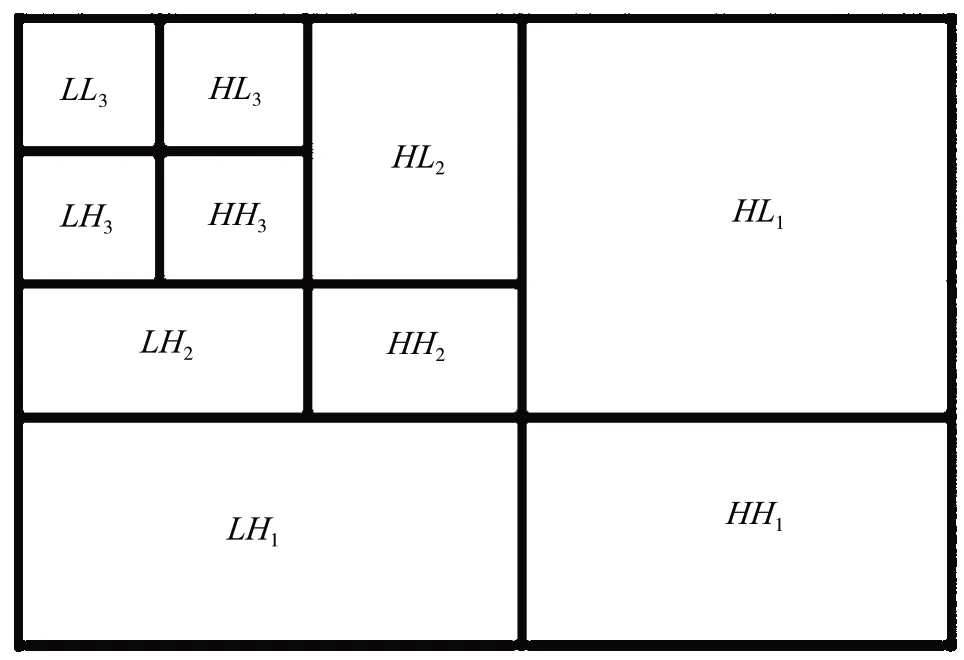
图1 图像的三级小波分解图
1.2 小波软、硬阈值去噪
由于信号在时间域往往具有一定的连续性,因此经小波变换后,信号的有效部分所产生的小波系数的模值相对较大;而噪声信号(如高斯白噪声)在时间域不具有连续性,所以经小波变换后,噪声信号的小波系数仍然具有较强的随机性,通常认为其服从高斯分布。由此得出一个结论:带噪信号经小波变换后,信号的有效部分对应的小波系数较大,而噪声部分对应的系数较小。
设噪声信号经小波变换后,小波系数对应的方差为σ,由高斯分布的特性可知,99%以上的噪声系数都位于[-3σ,3σ]区间内。因此,只要将[-3σ,3σ]区间内的系数置零,就能最大程度地抑制噪声。之后将经过阈值处理后的小波系数重构,就可以得到去噪后的信号。
估计小波系数的常用方法如下,取:

式中:σ是噪声标准方差,N为信号长度。
硬阈值估计方法定义为:
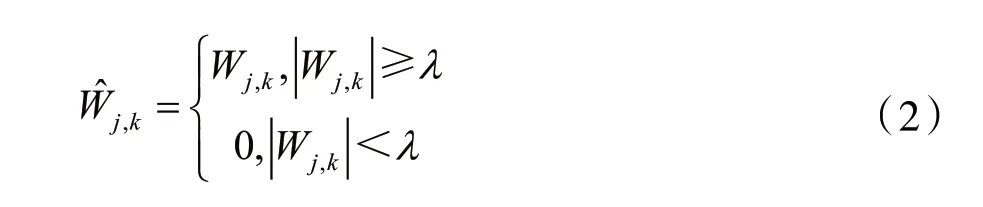
式中:Wj,k为真实的小波系数,为估计的小波系数。
与之对应的软阈值估计定义为:

式中:sign为符号函数。
2 改进的自适应贝叶斯小波阈值算法
2.1 现有方法存在的问题
现有的小波阈值算法存在如下问题:
(1)现有方法不能同时确定阈值和阈值函数;
(2)因硬阈值法在阈值处不连续,故通过该方法得到的图像会产生附加振荡从而产生伪吉布斯 效应[8];
(3)由软阈值函数估计得到的小波系数虽然整体连续性较好,但其估计的小波系数与原始小波系数之间存在恒定偏差,因此通过该方法得到的重构图像虽然平滑性能比较好,但会导致图像边缘模糊,损失图像的细节部分[9]。
因此,本文提出一种新的改进自适应贝叶斯小波阈值算法,对于图像的去噪非常有价值。
2.2 改进自适应贝叶斯小波阈值算法
小波阈值去噪的一个关键因素就是对阈值的估计。本文采取基于广义高斯分布(Generalized Gaussian Distribution,GGD)模型的阈值估计方法。该公式的建立基于经验观察,即通过零均值的广义高斯分布可以适当地概括自然图像子带中的小 波系数。
假设信号为[fij,i,j=1,2,…,N],N是2的幂,它被一加性随机噪声污染,记为:

式中:εij是独立同分布的均值为零的正态分布,并且独立于fij。
去噪的目标是得到fij的估计值,使均方误差(Mean Square Error,MSE)最小。

零均值的广义高斯分布GGD描述为:
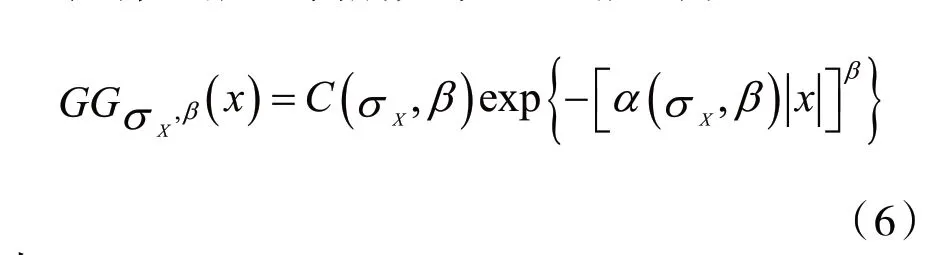
式中:-∞<x<∞,σX>0,β>0,
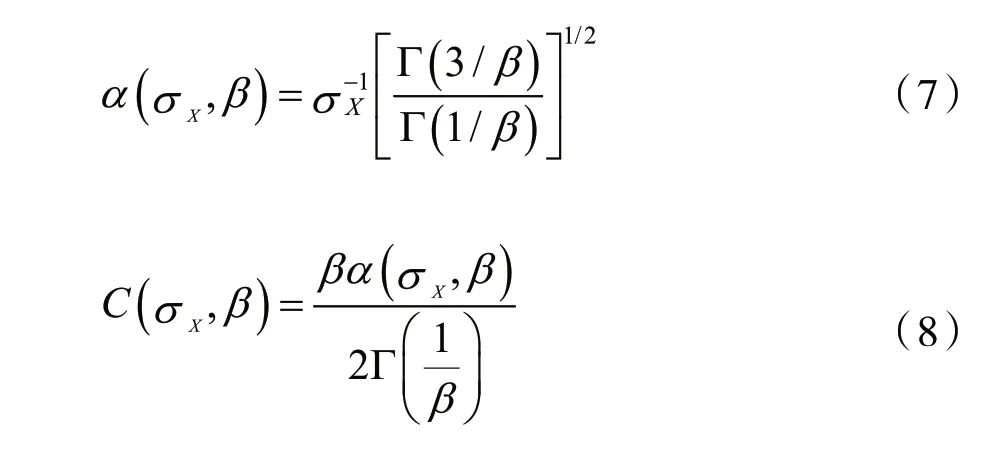

基于Bayes估计理论的去噪原理就是通过寻找一个阈值T,使得贝叶斯风险函数Y(T)最小,T的计算公式为:

用T*表示自适应最佳阈值,即:

对于GGD参数的估计,即σX和β,而对于σX和β参数的估计又产生了数据驱动的TB(σX)估计,以适应不同的子带特性。首先需要对噪声方差σ2进行估计,对此,可由Donoho提出的鲁棒中值进行估计,如下式:

因β参数没有显式解代入表达式TB(σX),只有信号标准偏差σX才有。因此,直接对σX或σX
2进行估计。由式(5)可知,观测模型为Y=X+V,且X、V之间是彼此独立的,由此可得:

σY
2是Y的方差,对于σY2的值可以由下式得到:

因子带的大小为n×n,于是得到TB(σX)的估 计为:
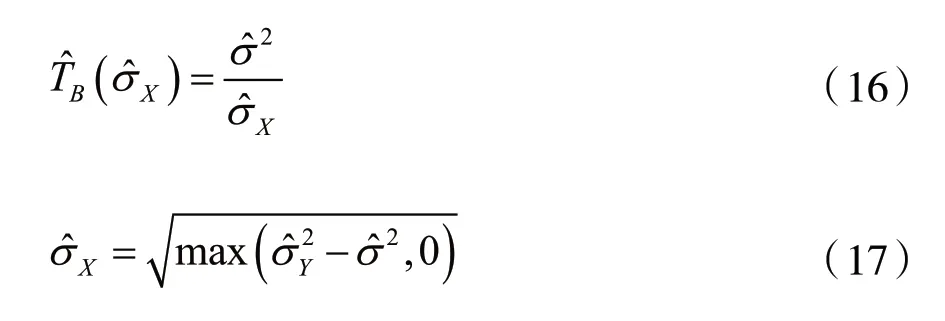
可得到最终的最佳自适应阈值为:
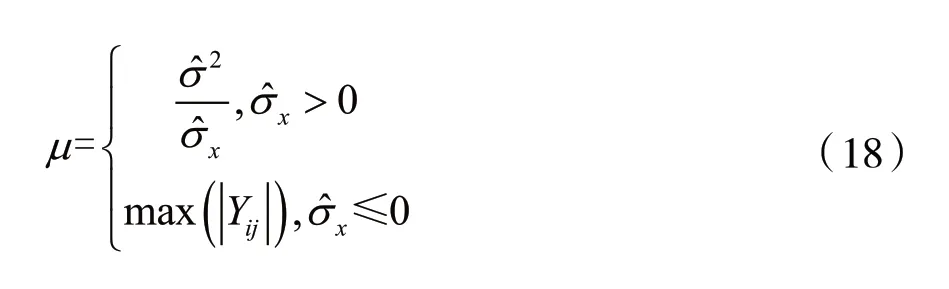
式中:σ为加入的高斯噪声方差,σX为不带噪声信号的标准方差,μ为最佳计算阈值。
阈值周围的小波系数值的滤除和保留程度由模糊度量中的一维距离比例函数来划分区域并确定,具体划分如下:本算法的模糊区域指的是阈值周围的高频小波系数,由于无法判断这些小波系数中含有噪声与否的情况,因此根据模糊区域的设定,根据含有噪声的程度大小,由三个区域即A1、A2、A3来划分小波系数的数值,如图2所示。

图2 基于模糊距离函数和贝叶斯最佳阈值的高频小波系数数值区域划分
对于A1区域,由相关理论与经验公式可知,小于0.9μ的小波高频系数是噪声一类,故全部进行置零清除。A1区域的函数表达式为

式中:Ai,j表示含噪声图像的小波系数,表示经过去噪之后的图像的小波系数。
对于模糊区域即A2部分,用中介模糊算法处理小波系数含噪声成分,根据一维模糊距离比例函数计算,确定小波系数,得到A2的表达式为:
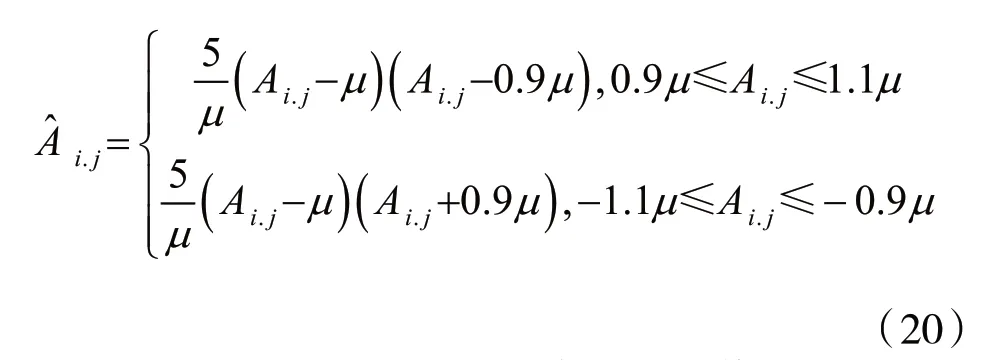
对于A3区域部分,为解决原软阈值函数中“恒定偏差”的不足,本文算法基于“软阈值的萎缩量尽量缩小”的思想,同时又根据“小波系数越大噪声程度越低”的结论,得到A3区域的表达式为:
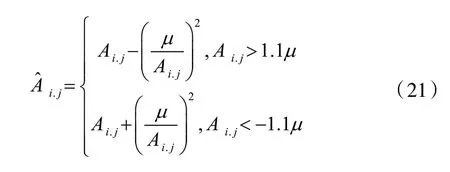
3 实验仿真与分析
3.1 算法整体流程
整体的自适应贝叶斯阈值算法流程如图3 所示。
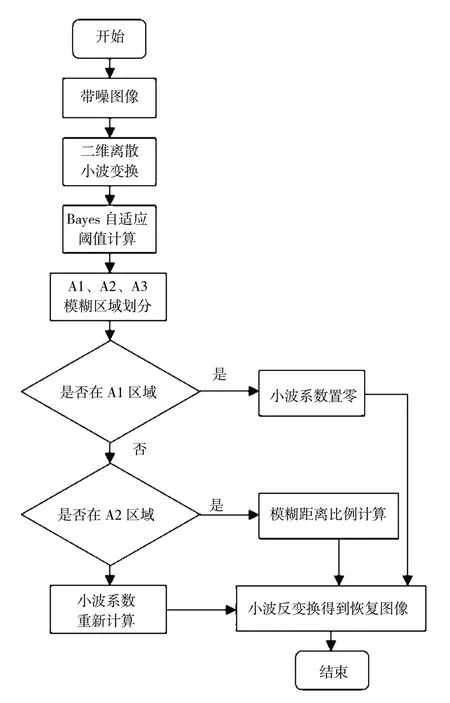
图3 自适应贝叶斯小波阈值算法流程图
3.2 结果分析
图像质量的评价标准可以分为主观评价与客观评价。主观评价可由人眼的视觉效果来评价,常用的客观评价指标有信噪比和均方差,分 别定义如下:
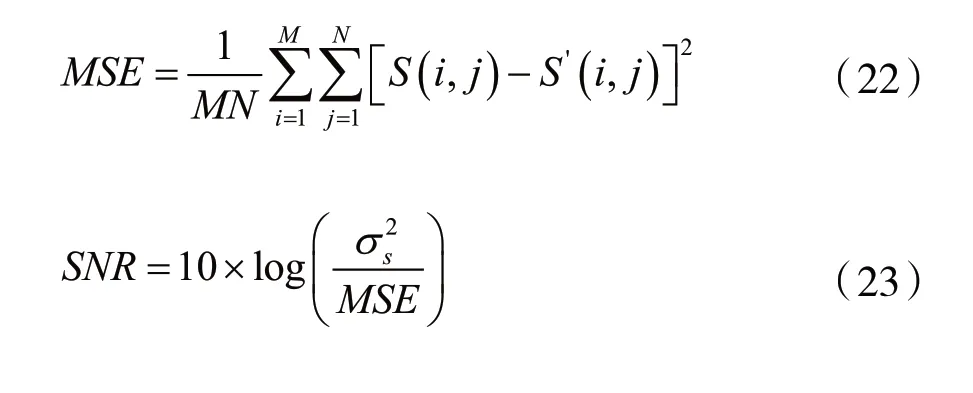
为了验证新阈值的性能,选择两张图片进行仿真实验。将图像Lena和House加入高斯白噪声,小波变换选用“sym wavelet”,分解层数为3层。分别从主观视觉与客观定量两个方面评价实验结果。视觉效果如图4~图6所示,定量评估了SNR和MSE参数。实验结果表明,将图4(f)和图5(f)与图4(d)、图4(e)和图5(d)、图5(e)进行比较,经本文所提的阈值去噪算法处理后的图像更清晰,边缘和纹理信息保存得更好。表1和表2的数据表明,无论是在图4中还是在图5中,通过自适应贝叶斯阈值方法计算的SNR最高,而MSE最低。

图4 不同阈值算法对Lena图像的去噪结果对比

图5 不同阈值算法对House图像的去噪结果对比

图6 其他图像本文去噪算法去噪结果直观图

表1 各阈值去噪算法应用于Lena和House图像的SNR(单位:dB)比较

表2 各阈值去噪算法应用于Lena和House图像的MSE比较
4 结语
本文在GGD模型中提出了一种改进的贝叶斯小波阈值图像去噪算法,利用阈值周围的小波系数是否含有噪声的模糊性,对该模糊区域通过自适应算法确定小波系数的保留程度。仿真结果表明,与传统的软、硬阈值函数相比,该算法可以有效去除图像噪声、提高信噪比、降低均方误差,且在保持图像边缘细节方面效果更好,因而人眼视觉效果更好,算法更加实用和有效。

