5R串联机器人运动学分析及其控制系统研究

李国洪，周琪钧

（天津理工大学 天津市复杂系统控制理论及应用重点实验室，天津 300384）

0 引 言

工业机器人作为一种经典的机电一体化机械数字装备，体现着人类智慧与机器人技术的发展成果，可实现生产制造的模块化、智能化，技术附加值高，应用范围广。作为信息化社会的新兴产业和先进制造业的支撑技术，全球各国都将其视为工业自动化发展的重点方向，势必将对未来生产生活和社会发展起着愈发重要的作用。

在工业机器人的运动控制方面，国内外众多学者都进行了广泛的研究。如Metin Toz[1]最新研究了一种基于混沌理论的全新涡旋搜索算法来求解带偏置腕的串行机械臂逆运动学问题，该算法具有较好的逆解寻优精度和收敛速度，但目前还停留在理论仿真尚未应用于实际。Matulis Marius和Harvey Carlo[2]利用数字孪生建模技术通过强化学习方式对机械臂进行虚拟现实分析，将数字世界与实体世界进行了完美融合。在国内，肖国红等人[3]开发了一款基于PLC控制的5自由度机械臂实验平台，该平台具有底座旋转、垂直与水平移动、手爪旋转与抓取等5个自由度。朱鹏程等人[4]运用Arduino控制器设计了一款五自由度机械臂与LabVIEW上位机，该系统可实现五自由度机械臂的基本功能，解决了实际本体实验成本较高的问题。相较于国内，国外研究者不论是算法还是研究方式均领先我国，再者我国机器人研究人才缺口巨大，高校还是采用传统大型工业示教系统的教学方式让学生普遍有畏难情绪，且系统本身也具有一定的危险性，学生的学习积极性并不高，所以，开发一种经济性、直观性好的工业机器人控制试验系统具有很强的现实意义[5]。

本文根据工业生产中5R（转动副）工业机器人结构特点，首先采用DH参数法建模，建立起工业机器人运动学模型，采取坐标变换矩阵推导出机器人运动学方程，进行正逆运动学求解，运用Matlab软件中的Robotics Toolbox进行机器人工作空间和轨迹规划的仿真求解。最后通过搭建基于STM32F407的机器人控制系统与PC上位机进行实物联合试验，进一步验证了运动学模型的正确性和机器人控制系统设计的合理性。

1 机器人DH参数建模

本文搭建的是5R抓取机器人系统，该系统的末端执行器具有5个自由度，即n末=5。其中，从下往上数的前3个转动关节主要控制执行器的空间位置，而后2个转动关节主要控制执行器的姿态，通常来讲，控制执行器抓手开合的自由度一般不包含在n末中。图1所示为5R抓取机械臂的DH坐标系机构图。

抓取机械臂可以视为是一系列由运动关节串接起来的连杆组成的，为每一连杆构建一个坐标系，并用齐次变换来描述这些坐标系之间的相对姿态和位置。本文5R机械臂DH参数如表1所示。

表1 5R机械臂DH参数

由于Matlab拥有强劲的矩阵运算能力和特有的Robotics Toolbox，采用该工具箱中的Link函数和Robot函数即可构建机械臂各个关节的模型方程，该函数的一般表达式为：

使用Robotics Toolbox中的Link函数创建该机器人的命令为：

L1 = Link（[0 85 0 0 0],‘modified’）；

L2 = Link（[–π/2 0 10 –π/20],‘modified’）；

L3 = Link（[0 0 105 0 0],‘modified’）；

L4 = Link（[0 0 90 0 0],‘modified’）；

L5 = Link（[0 100 0 –π/20],‘modified’）；

robot = SerialLink（[L1,L2,L3,L4,L5]）；

robot.name = ‘5R抓取机器人’；

robot.plot（[0,–π/2,0,0,0]）；

robot.display（）；

运行如上Matlab代码后，即可获得如图2所示的机械臂模型图[6]。若加入teach指令，则可通过左侧滑竿框调节各个关节的角度位置，实现姿态调整，如图3所示。

图2 机械臂DH参数模型姿态图

图3 姿态调整图

2 机器人运动学分析

2.1 5R机械臂正运动学分析

已知机械臂各个关节的转动角度，求取机械臂工具端OT的姿态和位置，即为机械臂的正解。用坐标变换来描述从坐标系0～0T5的变换。由图1可知，从坐标系1到坐标系0的变换矩阵为0T1。以此类推1T2、2T3、3T4和4T5。

已知相邻连杆i与i–1之间的连杆变换通式为：

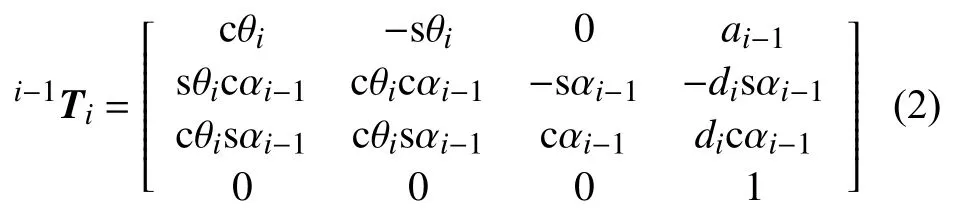
其中，s和c分别表示三角函数sin和cos。

根据连杆变换的齐次矩阵式（2）和表1的连杆参数，运用D-H法求得各连杆变换矩阵如下：

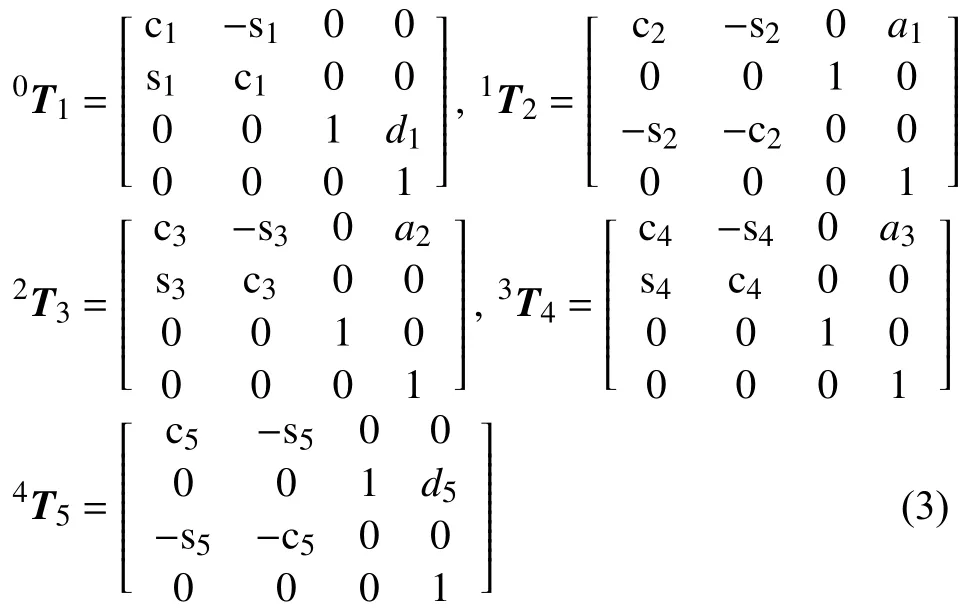
其中，ci=cosθi、si=sinθi。

5R机械臂的运动模型是由以上5个坐标变换矩阵相乘得到的，这样即可得到该机械臂的运动学模型：

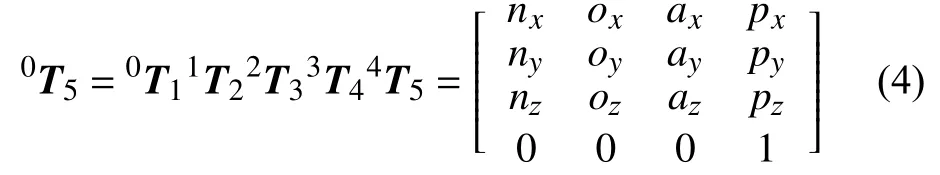
机械臂末端位置方程为：

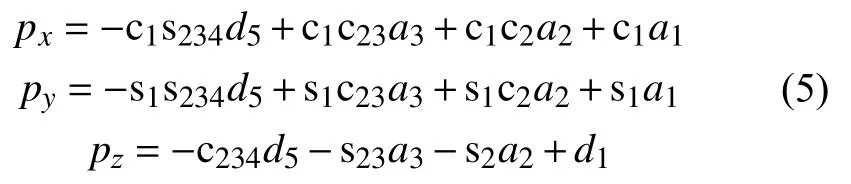
其中，sij=sin（θi+θj）、cij=cos（θi+θj）、sijk=sin（θi+θj+θk）、cijk=cos（θi+θj+θk）。

2.2 5R机械臂逆运动学分析

逆向运动学分析指已知末端执行器（机械爪）位姿的前提下，求解运动方程，即求得机械臂相应各个关节角度。这对于机械臂的运动控制至关重要。根据0T5可以知道机械臂的运动位置和姿态，需要获得各关节的坐标值，用以机械臂能够被驱动至这个位姿。

其中，K1=c1px+s1py−a1−d5c1ax−d5s1ay、K2=pz−

d1−d5az、K3=c1px+s1py−a1−a2c2−d5（c1ax+s1ay）+d5az+d1−pz−a2s2。

根据上面各式的结果来看，机械臂的运动反解可能存在多种解。但由于机械臂结构的约束，例如各关节变量可能不会全都在360°范围内可运动，有些解不可能实现。在其存在多种解的情况下，应择其最满意的一组解，例如：选择一组与机械臂当前位置最接近的解，或者考虑避障要求等，以满足机械臂实际工作需求。

3 机器人运动学仿真

3.1 机械臂工作空间仿真

通常来讲，机械臂的工作空间指的是末端执行器经历所有可能的运动后末端遍历的全部体积，它是衡量一款机械臂工作能力的一项重要运动学指标。将本文5R机械臂的工作空间记为S（P）。则工作空间和各个关节变量的关系可以用下式表达：

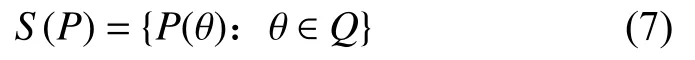
式中：θ=[θ1，θ2，θ3，θ4，θ5]——关节变量；

Q——约束空间，切莫随意取值，应考虑实际情况确定约束空间：

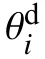
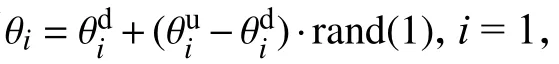
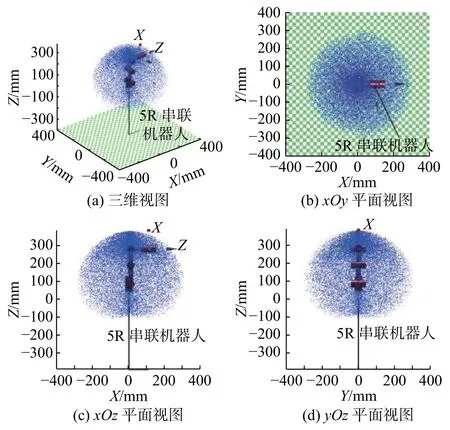
图4 机械臂工作空间云图

由图4可以直观地看出，机械臂在笛卡尔坐标系中三个方向上的运动基本上可以达到最大范围内的所有空间。在实际的生产作业中，根据机械臂的位置数值可以分析得到其工作空间的边界条件继而知晓其运动范围，通过将机械臂及相关工件进行合理配置，可实现场所利用率的最大化利用。

3.2 机器人轨迹规划仿真

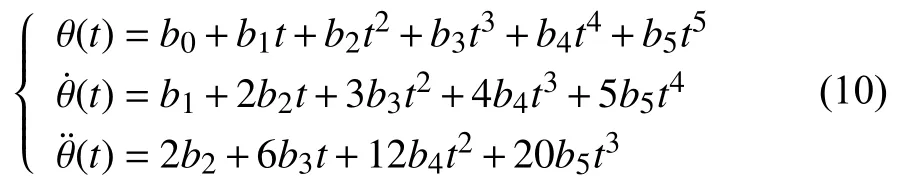
根据以上边界约束条件，即可得到插值函数中b0～b5各值。

jtraj函数调用的格式为：[q qd qdd]=jtraj（qz,qr,t）其中，q为关节位置，qd为关节角速度，qdd为关节角加速度；qz为初始位置关节角的值，qr为终止位置关节角的值，t为轨迹运行的时间。

本文规划的路径轨迹是从 q1=[0，–π/2，0，0，0]运动到 q2=[π/2，–π/3，–π/4，–π，0]的曲线。

则有 qz=q1，qr=q2，设定时间t=[0∶0.1∶5]，总运行时间为5 s，采样周期为0.1 s。

对该机械臂各关节角度位移、速度及加速度进行规划仿真，可得到各关节物理量（角位移、角速度、角加速度）随时间的变化曲线和轨迹路径如图5所示。

图5 机械臂关节角位移、角速度、角加速度变化曲线及轨迹路径

由图5可以观察到各个关节三个物理量（角位移、角速度、角加速度）随时间变化的情况。从三幅图中可以直观地看到每个关节独立运动互不干扰，并且各关节起点和末点速度与加速度为零，轨迹保持平滑连续。

4 机器人控制系统设计

4.1 控制器系统电路设计

以STM32F407嵌入式单片机为核心，设计了控制机械臂六组电机（包括工具端执行器电机）的硬件电路。该电路包含STM32F407最小系统、JTAG调试电路、芯片供电电路、滤波电路、FLASH存储电路、USB转串口电路、电机接口电路、RS485和CAN通信电路、按键、蜂鸣器和LED指示灯电路等。硬件电路原理图由Altium公司发布的 Altium Designer（in AD19）软件设计。控制系统框图如图6所示。

图6 控制系统框图

4.2 控制系统软件设计及上位机介绍

该控制系统采用C程序设计进行软件开发，KEIL MDK5为开发工具。图7为控制系统软件流程示意图，该流程主要由主程序和中断服务子程序构成。主程序包含系统初始化、机械臂初始位姿设定及其控制参数初始化，系统初始化又包含LED和蜂鸣器初始化、定时器TIM初始化、ADC初始化、中断配置和串口通信配置等。中断服务子程序主要由3个中断服务函数构成，包括判定电机供电是否正常的定时器中断TIM2服务子函数、接收判断PC上位机监控软件指令的串口中断USART1服务子函数和输出电机控制PWM的定时器中断TIM3服务子函数。在main函数主循环中，TIM2中断优先级最高，全程一旦检测到电机供电异常，蜂鸣器就会报警提示；串口中断USART1优先级次之，其主要任务是接收并判断上位机指令是否符合既定控制指令并将其提取出来；TIM3中断优先级最低，其主要任务是将提取到的控制指令转换为相应的PWM输出，驱动机械臂对应关节运动，使之完成相应指令。

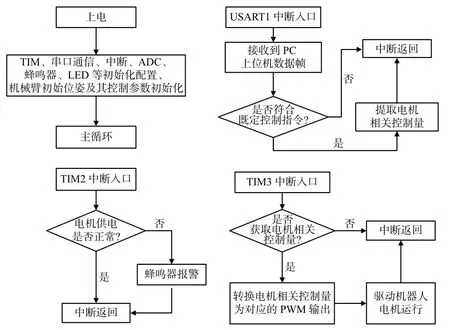
图7 控制系统软件流程框图

PC上位机监控软件采用微软发行的Visual Studio软件C#语言开发。软件界面如图8所示。采用上位机控制机械臂前，首先将micro-USB线缆连接控制板USB串口和计算机USB接口，再选定所用的串口号并设置好波特率后，即可对机械臂进行操作。该上位机设计有2种模式，分别为正、逆运动学演示模式。在正运动学模式中，上位机可以控制每台电机的运动并且用户能自主设计机械臂的运行动作；在逆运动学演示中，输入起、终点坐标，机械臂可以平滑地由起点运行到终点，若运行不到或失败，则有相应的警告提示，体现出逆运动学。

图8 上位机监控软件界面

5 系统试验

根据上节所设计的机器人控制系统，完成机械臂与控制板及PC上位机的连接与安装，图9为STM32机械臂控制板实物图，图10为机械臂控制试验系统连接图。

图9 STM32F4控制板

图10 机器人控制系统连接图

首先，连接机械臂与控制板。整个过程中要确保各连线准确无误，同时保证电源开关等关键部件是否工作正常。当一切准备就绪后，则可对机械臂进行控制。

为了验证前文所述轨迹规划的正确性，设计一条从起点[0–π/2 0 0 0]运动到终点[π/4–π/2–π/2–π/3 0]的曲线。运用Matlab中所搭建的模型仿真，并取轨迹中的5个点为测试点，通过Matlab可获得这5个点各自所对应的各电机角度理论值（见表2）。

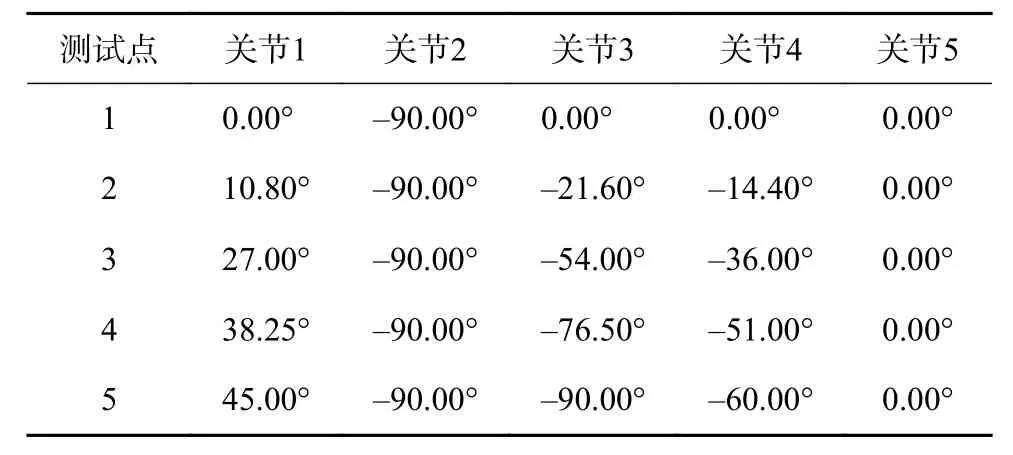
表2 测试点关节角度（Matlab获得）

然后将这5个点换算成对应的空间坐标，输入到PC上位机逆运动学界面的坐标输入窗口中（见图8），运行后可根据Visual Studio的控制台窗口查看测试点所对应的各电机实际要驱动的角度（见表3）。通过将两表进行对比，可发现各测试点仿真与实际中各电机转动角度差别很小，考虑到系统开发过程中实物平台的测量误差和实物刚性的问题，可证明系统逆运动学编程开发的正确性和轨迹规划的合理性。

表3 测试点关节驱动角度（Visual Studio算得）

整个试验过程中，机械臂运转正常，较准确经过所要求的路径点，响应速度快，各关节之间运行平稳、连续无停顿，表明该机械臂控制试验系统基本符合要求。

6 结束语

首先采用D-H参数建模法建立了工业机器人运动学模型，进而采用坐标变换矩阵推导出其运动学方程并进行正逆运动学求解。接着运用Matlab进行运动学仿真，根据Monte Carlo法和jtraj函数对机械臂的工作空间和轨迹规划进行求解。在最后的实物验证中，虽然试验结果基本符合预期，但实验过程都是在无障碍无干扰的理想环境中进行的，而实际情况并没有这样简单，所以接下来的计划是：1）在存在干扰因素的情况下对机器人进行轨迹规划；2）解运动方程过程中若涉及方程非线性问题，可能导致无法推导出解析解，这时又应作何处理；3）文本研究的内容，暂不涉及动力学，而实际情况需将其考虑进去以达到更优的控制效果。