五自由度机器人运动控制与空间位姿仿真系统
庄衡衡,丁 飞,章华涛,张海涛,暴建民
(1.南京邮电大学 江苏省宽带无线通信和物联网重点实验室,江苏 南京 210003; 2.南京邮电大学物联网学院,江苏 南京 210003; 3.中国科学院国家天文台南京天文光学技术研究所,江苏 南京 210042; 4.中国科学院天文光学技术重点实验室,江苏 南京 210042)
0 引 言
随着我国先进制造技术的发展,多自由度机器人以其自动化、高效化和智能化优势,将在高端制造、空间遥操作和智能自主系统等领域获得广泛应用[1-2]。多自由度机器人的运动控制影响位姿的可达工作空间与目标指向精度[3],两者之间的有效协同将直接决定多自由度机器人的工作性能[4-5]。因此,研究并建立多自由度机器人的运动控制和空间位姿的协同分析与仿真系统具有重要意义。
作为机器人运动控制、位姿调整[6]的核心计算模块,对正向运动学和逆向运动学的求解是关键。郭万金等[7]针对一种五自由度机器人提出了逆运动学的封闭解法。张道义等[8]用矢量法和求导法分别对五自由度雕刻机末端运动学进行正向和逆向速度的分析。Cao F等[9]提出了一种基于SCARA的新型五自由度焊接机器人,采用DH模型得到正、逆运动学的一般公式,同时利用ANSYS软件对其进行了模态分析。Lee J W等[10]指出工业机器人制造商和用户大都专注于使用激光跟踪器对机器人进行空间位姿精度测试。Zheng K等[11]对5-DOF混联乒乓球机器人的机械臂进行空间位姿分析,将工作空间中的球拍姿势转换为联合空间中驱动轴的参数,并使用ADAMS软件进行运动模拟。
上述研究为多自由度机器人的运动控制与空间位姿分析奠定了良好基础。本文提出一种五自由度机器人运动控制与空间位姿仿真方法,首先对五自由度机器人进行运动学建模,然后推导了其正向运动学和逆向速度运动求解方法,最后设计并实现了其运动控制与空间位姿协同仿真系统,为后续多自由度机器人的结构优化和可达工作空间分析提供分析平台和理论支撑。
1 运动学建模与求解
1.1 五自由度机器人结构模型
本文的五自由度机器人结构模型如图1所示,该机器人由三自由度的平动机构和两自由度的转动机构共同构成,其中前3个自由度分别定义为沿着X轴,Y轴和Z轴向的平动,O1、O2和O3分别为平动关节轴X轴,Y轴和Z轴上的关节节点,Ox,Oy和Oz分别为O1,O2和O3在各自平动轴上运动的起始点;根据平动关节轴的定义方向,后两个自由度分别定义为沿着X轴和Y轴向的转动,O4和O5分别为转动关节轴X轴和Y轴向上的关节节点,c2,a4和b5分别为O1与O2,O3与O4和O4与O5之间的相邻关节点的结构偏置,末端执行器安装在关节节点O5上,在其上定义指向节点P,且两个转动关节轴的起始角度如图1(a)所示。
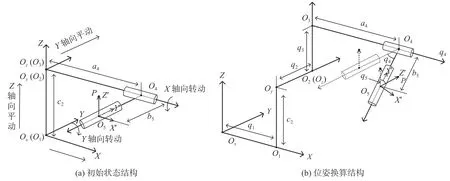
图1 五自由度机器人的结构模型
为了方便描述经过五自由度的平动、转动变后末端执行器的指向,在机器人的结构模型中定了2个坐标系,一个是基础坐标系XYZ,另一个是过五自由度变换后的末端坐标系X′Y′Z′。其中义末端坐标系各坐标轴的正方向为基础坐标系各标轴的正方向经过五自由度平动、转动变换之后指向,且在末端执行器的初始位姿下,末端坐标与基础坐标系的各坐标轴的正方向保持一致。关节点O1、O2、O3、O4、O5和P的位置均用基础坐系描述,定义末端执行器的指向沿着末端坐标X′Y′Z′中Z′轴的正方向,因此指向节点P也定义在轴上,则末端执行器的指向沿着O5点到P点的方五自由度机器人的结构调整分别由各自运动上的高精度伺服电机驱动,均可在各自的运动轴沿着正、负两个方向进行运动,且运动的正方向图1(a)所示。通过对5个伺服电机的高精度协控制[12],调整五自由度上机械臂的位姿,从而实机器人末端执行器的位姿控制与精确对准。
1.2 正向运动学求解
正向运动学是在已知各关节点的初始位置、相邻关节点间的结构偏置等参数的前提下,结合相关节点间的相对运动量,求解末端执行器位姿的程[13]。在平动关节轴X轴,Y轴和Z轴上分别调整q2和q3的位移量,转动关节轴X轴和Y轴上分别调q4和q5的旋转量,经过五自由度的平动和转动变调整后的状态模型如图1(b)所示。
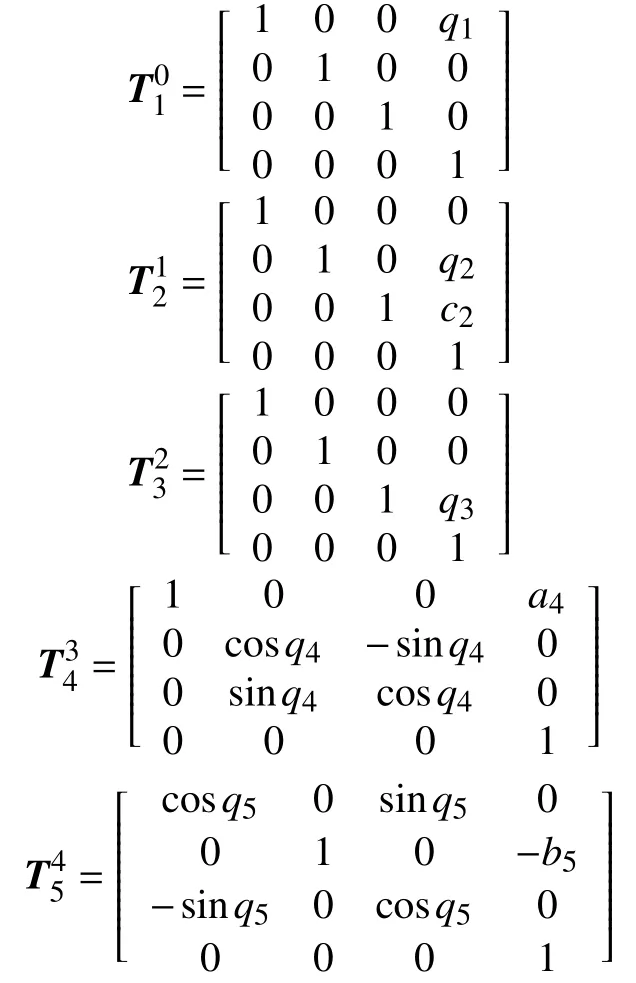
将上述矩阵依次相乘,得到末端执行器相对于基础坐标系XYZ的等价齐次变换矩阵:
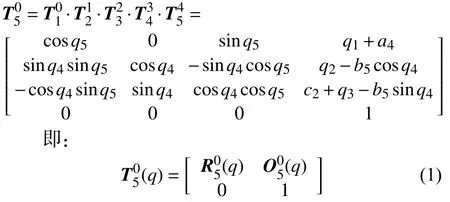
其中,相邻关节点间的相对运动量向量为:q=(q1,q2,q3,q4,q5)T;旋转矩阵为:
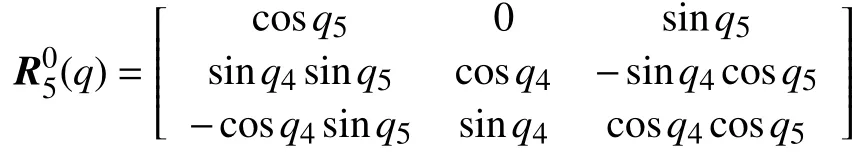
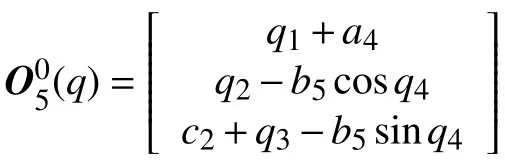
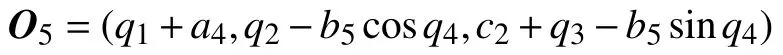
而末端执行器上的指向节点:
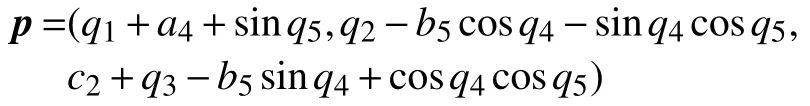
根据O5点的坐标和O5点到P点的指向,即可确定末端执行器相对于基础坐标系的位姿:
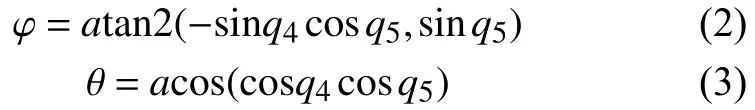
当使用ZYZ型欧拉角来描述末端执行器的指向时,在不考虑最后一个旋转轴Z轴自转的情况下,目标指向在地平式坐标内的方位角如公式(2),Z轴沿逆时针方向旋转为正;目标指向在地平式坐标内的天顶距如公式(3),Y轴沿顺时针方向旋转为正。
1.3 逆向速度运动学求解
逆向运动学是通过末端执行器的当前位姿和目标位姿,反解出相邻节点间相对运动量的过程[14-16]。与速度运动学相结合[17],就是在已知末端执行器当前位姿和目标位姿的前提下,将末端执行器由当前位姿向目标位姿运动时的线速度和角速度与关节速度矢量联系起来,并把关节速度矢量乘以电机的扫描时间间隔作为各个关节的调整量。
已知当机器人移动时,关节变量和末端执行器的位置都将是时间的函数。而角速度只要是相对于同一个坐标系来描述,就可以作为自由矢量相加,因此通过表示每个关节在基础坐标系上的角速度,相加来确定末端执行器相对于基础坐标系的角速度。结合本文的五自由度机器人结构,在使用ZYZ型欧拉角的旋转轴定义,且不考虑最后一个旋转轴 Z轴自转的情况下,末端执行器相对于基础坐标系的总的角速度矢量:

当末端执行器的目标位姿是固定值时,目标指向的速度方向向量恒为零向量,则当前指向调整到目标指向所需要的方向向量就是目标指向和当前指向间的方位角误差,且在一定的时间间隔内计算时,可以把所有的距离变量当作速度值。
那么末端执行器的线速度:

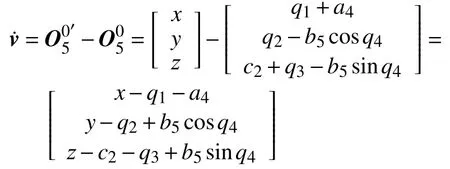
综上,得到表达式:

其中Jv和Jω都是3×5的矩阵,5表示机器人结构中共有5个自由度,因此得到速度运动学方程[18]:

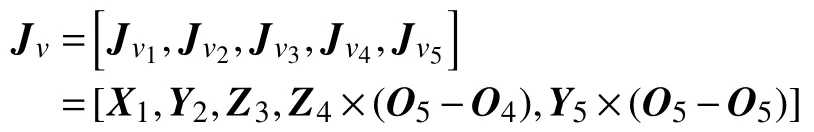
雅可比矩阵的下半部分Jω由下式给出:
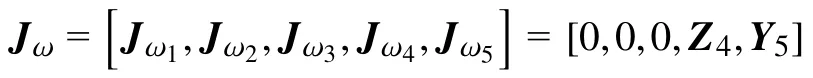
其中前3个平动关节对应的Jωi=0,后2个转动关节对应其各自运动轴的单位方向向量。
综上,根据速度运动学公式得:

其中J−为雅可比矩阵的伪逆矩阵,代入计算出,即五自由度上的速度调整量,用乘以电机的扫描时间间隔得到5个电机对应的运动调整量。
2 空间位姿仿真设计
五自由度机器人运动控制与空间位姿仿真系统的逻辑框架如图2所示,该系统从功能逻辑上分为控制侧与仿真侧,其中控制侧的主要功能为多自由度驱动单元的协同控制,核心的计算模块是对正向运动学和逆向速度运动学的求解,从而确定末端执行器的当前位姿和向目标位姿调整时多自由度驱动单元各自的调整量,最后当调整后的位姿与目标位姿之间的相对误差超过预设的误差量级时,触发位姿反馈。仿真侧的主要功能是对控制侧的特定业务流程进行数据同步,再对末端执行器当前的初始位姿进行计算,同时对动态调整过程中的阶段性位姿进行在线仿真,最后对目标位姿进行误差校验与评定。
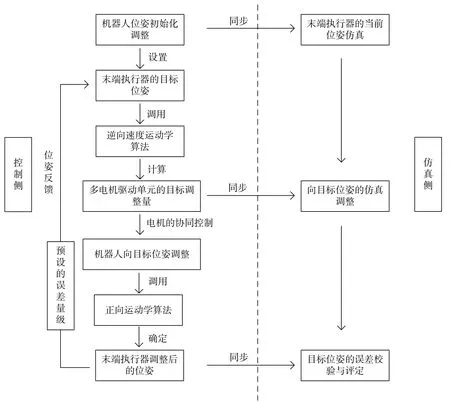
图2 仿真系统的逻辑框架
五自由度机器人位姿初始化调整的业务流程如下:
1)控制程序调用各电机驱动器的驱动接口,与5个高精度伺服电机建立通信连接。
2)连接完成后,程序读取伺服电机的轮上码值,并进行硬件定义上的回原点,调整后通过正向运动学算法,计算出末端执行器的当前位姿。
3)程序调用逆向运动学算法,控制末端执行器运动到初始工作位姿(软件定义上的回原点)。
五自由度机器人位姿仿真过程如下:
1)控制程序读入末端执行器的目标位姿,调用逆向速度运动学算法,计算出五自由度上电机各自的调整值。
2)通过标准化控制接口,传输控制信号给5个伺服电机。
3)电机运动完成后,进行位姿校准,程序读取电机的轮上码值,调用正向运动学算法,确定末端执行器调整后的位姿。
在上面的执行过程中,如调整后的位姿与目标位姿之间的相对误差超过预设的误差量级,此时将触发位姿反馈,重复上述操作直至调整后末端执行器的位姿符合预设。
3 实验与分析
五自由度机器人的运动控制软件采用Visual Studio开发环境,集成了Matlab软件开发的末端执行器的位姿在线仿真平台,两者之间协同完成仿真任务。仿真实验时,可以给定一组结构参数:c2,a4,b5分别取1.115 m,0.340 m,−0.145 m,选取一个马鞍面作为五自由度机器人的作业任务面进行运动控制与位姿仿真,其数学方程为:
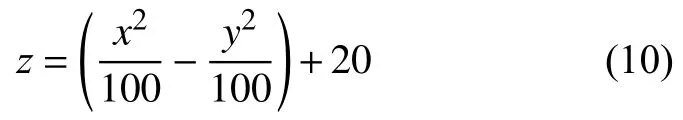
其中,取值范围:−0.400 m≤x,y≤0.400 m,Δx=Δy=0.020 m。
图3为根据马鞍面数学方程得到末端执行器的目标位置仿真图。末端执行器的指向取目标位置所在XY平面内的原点到目标位置的方向,此时末端执行器的位姿空间分布如图4所示,俯视图如图5所示,其中相邻且颜色不同的两个点间的方向构成了末端执行器的指向。
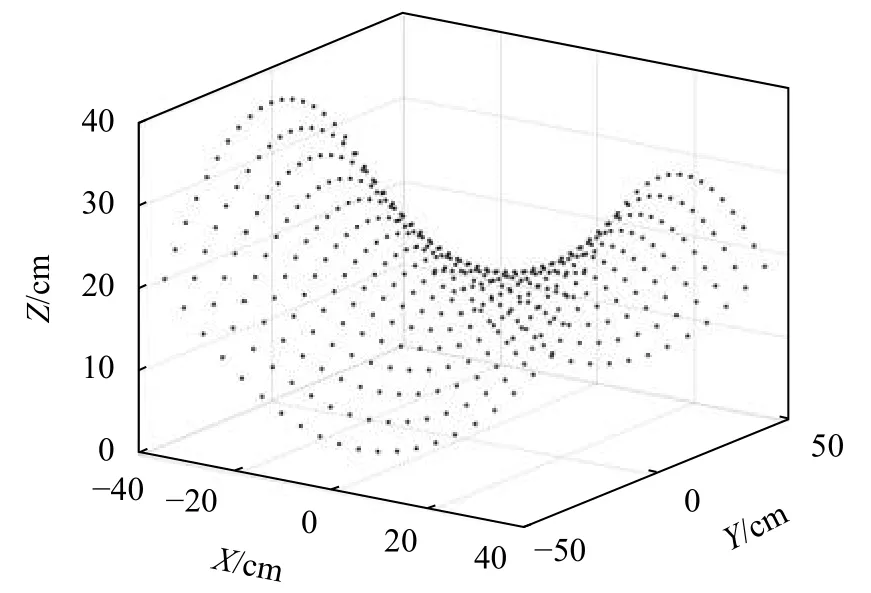
图3 末端执行器的目标位置仿真图
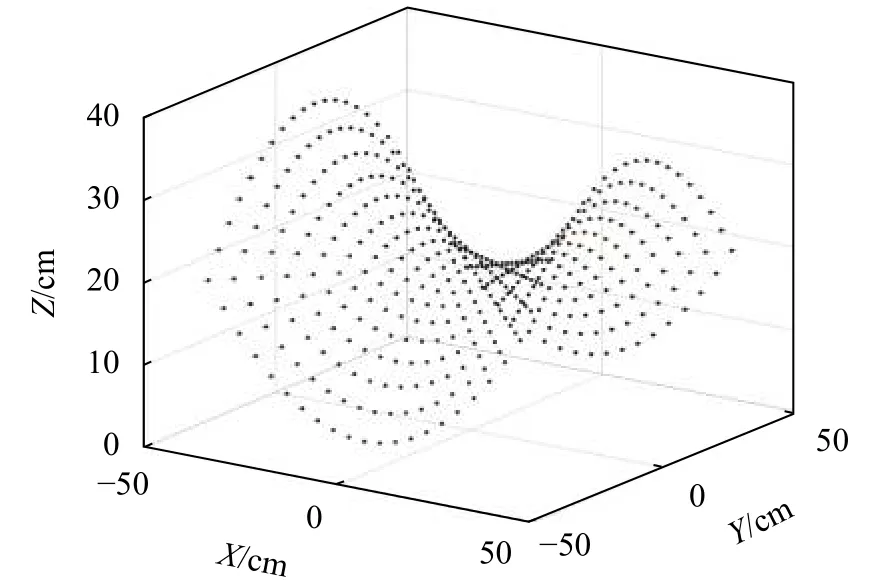
图4 末端执行器的空间位姿仿真图
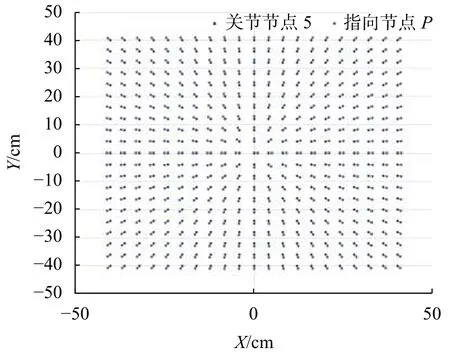
图5 末端执行器位姿仿真俯视图
定义末端执行器目标位姿的位置(Tx,Ty,Tz)和指向(Tφ,Tθ),调整后末端执行器位姿的位置(Cx,Cy,Cz)和指向(Cφ,Cθ)。当末端执行器调整后的位姿与目标位姿之间的误差≤10−4m时,视为调整完成,此时定义对应点的位置误差Δd和指向误差Δδ分别为:
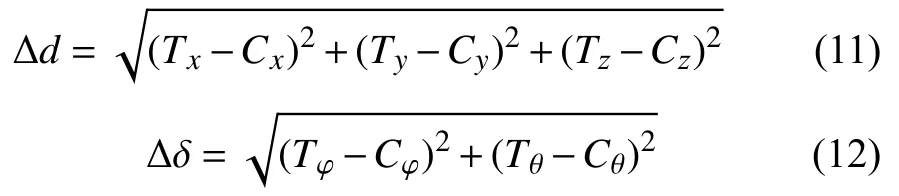
计算得到仿真位姿最大的位置误差为:Δd=3.624 159 774 613 950×10−13m,指向误差为:Δδ=1.998 894 815 878 120×10−14rad,发现两者相对误差非常小,因此该数值验证了所提出的正向运动学和逆向运动学解法正确有效。
对五自由度机器人进行运动控制与空间位姿仿真,通过控制程序,调整末端执行器到达预设的起始工作点,末端执行器起始位姿和目标位姿的参数如表1所示。

表1 末端执行器起始位姿和目标位姿的参数
五自由度机器人的空间位姿仿真结果如图6所示,图中展示了对机器人三次静态位姿下各个关节节点和指向节点的位置,其中指向节点上的数字0、1和2分别表示位姿调整的次数,第0次表示机器人的起始结构位姿,则末端执行器由起始位姿向目标位姿共调用运动学算法并调整了2次。计算第2次调整后相应的位置误差与指向误差,误差结果均为0,结果表明该机器人运动控制与空间位姿仿真系统准确有效。
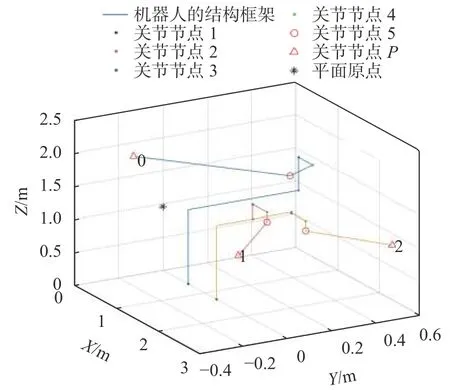
图6 五自由度机器人空间位姿仿真图
4 结束语
本文设计并实现了一款五自由度机器人运动控制与空间位姿仿真系统,针对五自由度机器人进行运动学建模,提出了正向运动学和逆向速度运动学求解方法,并选取马鞍面为作业任务面进行在线仿真,数值计算结果表明末端执行器的仿真位姿与目标位姿具有一致性,验证了仿真系统的可行性与工作稳定性。该仿真系统可实现五自由度机器人的运动控制与位姿仿真的一体化,为后续多自由度机器人的结构优化、可达工作空间分析与性能评估提供平台支撑与技术基础。

