基于高斯混合-隐马尔可夫模型的特种设备敲击检测
余焕伟,陈仙凤,朱先华,赵星波,杜锡勇
(1.绍兴市特种设备检测院, 绍兴 312000;2.嘉兴市南湖区社会福利保障指导中心,嘉兴 314001)
敲击检测属于声振无损检测方法的一种[1],最早用于车轮的完整性检测,现应用范围逐渐扩大到陶瓷[2]、航天复合材料[3]、蠕墨铸铁件[4]、风力机叶片[5]检测等领域。在特种设备检测中也常使用检验锤敲击锅炉进行宏观检验[6],可以对金属材料的开裂、劣化、腐蚀、结垢等进行初步判断。
降低敲击检测主观性的传统方法是利用传感器记录下敲击对象声振的幅值频率等信息,通过对敲击信号时频域特征参量的研究来判断被检对象的缺陷或故障状况[7-8],再结合具体模型进行故障诊断[9-10]。上述方法主要从声振检测理论出发,比较依赖信号处理技巧和专家的知识经验,在实际应用中有一定的局限性。文章将在对敲击信号频域特征分析的基础上,借助于智能语音识别技术,提出一种基于改进的高斯混合-隐马尔可夫模型(GMM-HMM)的敲击检测模型,模拟检测人员从敲击中“听出”缺陷的过程,并通过试验对模型的有效性和鲁棒性进行验证。
1 隐马尔可夫语音识别理论
HMM(隐马尔可夫模型)以概率统计理论为基础,广泛应用于语音识别等多个领域[11-12],其包含了两个双随机过程,可用参数{S,X,Π,A,B}来描述:
S=(s1,s2,…,sN-1,sN)
(1)
X=(x1,x2,…,xM-1,xM)
(2)
Π=(Π1,Π2,…,ΠN-1,ΠN)
(3)
A=[aij]N×N,aij=P(qt+1=sj|qt=si),
1≤i,j≤N
(4)
B=[bjk]N×M,bjk=P(ot=vk|qt=sj),
1≤j≤N,1≤k≤M
(5)
式中:S为隐藏状态;N为隐藏状态数;X为L维的观测状态序列;M为观测状态数;Π为状态初始分布概率;A为状态转移概率矩阵;aij为从时刻t到t+1时状态si转移到状态sj的概率;qt,ot分别为t时刻的隐态状态和观察状态;B为状态发射矩阵;bjk为t时刻隐藏状态sj生成观察状态vk的概率。
文章利用HMM实现两个目的:① 学习训练,给定观测序列样本集X,寻找最佳的HMM参数{S,Π,A,B};② 模式识别,给定HMM参数和观测序列X,求解概率最大的隐藏状态序列S。
当X为连续值时,bjk可用GMM(高斯混合模型)(μ,σ,w)来描述[13],其中μ,σ分别为序列X的平均值和标准差,w=(w1,w2, …wm)为高斯子分布权重,m为高斯子分布数。
采用EM(期望最大化)算法对GMM-HMM参数{Π,A,(μ, σ,w)}进行迭代更新,采用Viterbi 算法计算模型的总输出概率,当收敛率RC满足式(6)时停止迭代。
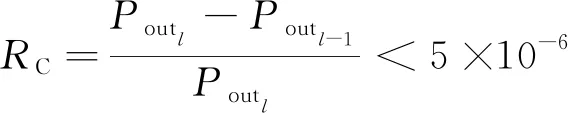
(6)
式中:Poutl-1,Poutl分别为模型在第l-1次、第l次迭代时的总输出概率。
2 敲击检测系统及信号采集
2.1 模拟试件与敲击检测系统
试验制作人工试件来模拟金属部件存在的凹坑、开裂、夹层、局部减薄、对接焊缝、环向裂纹等情况。1#平板试件无缺陷,2#平板试件底部开孔,3#平板试件的边缘至中心设有垂直表面的开裂缺陷,4#平板试件一半厚度处设有夹层缺陷,5#平板试件底部的中心减薄,6#平板试件设有对接焊缝,7#钢管试件一半长处设有环向裂纹,8#钢管试件的端部焊缝处设有环向裂纹,9#钢管试件无缺陷。平板试件的尺寸均为400 mm×400 mm×30 mm(长×宽×高),无缝钢管试件尺寸(直径×壁厚)为50 mm×3 mm,长度为1 000 mm, 材料为低碳钢。信号采集系统主要包括动态信号测试分析仪、力锤、加速度传感器和声音传感器,其组成如图1所示,系统采样频率为51.2 kHz,图2为该系统在1#试件上采集到的连续30次敲击的声信号。
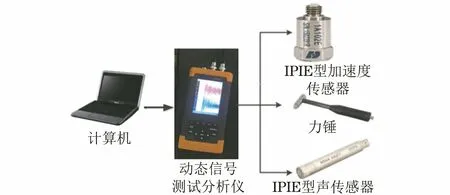
图1 敲击信号采集系统组成
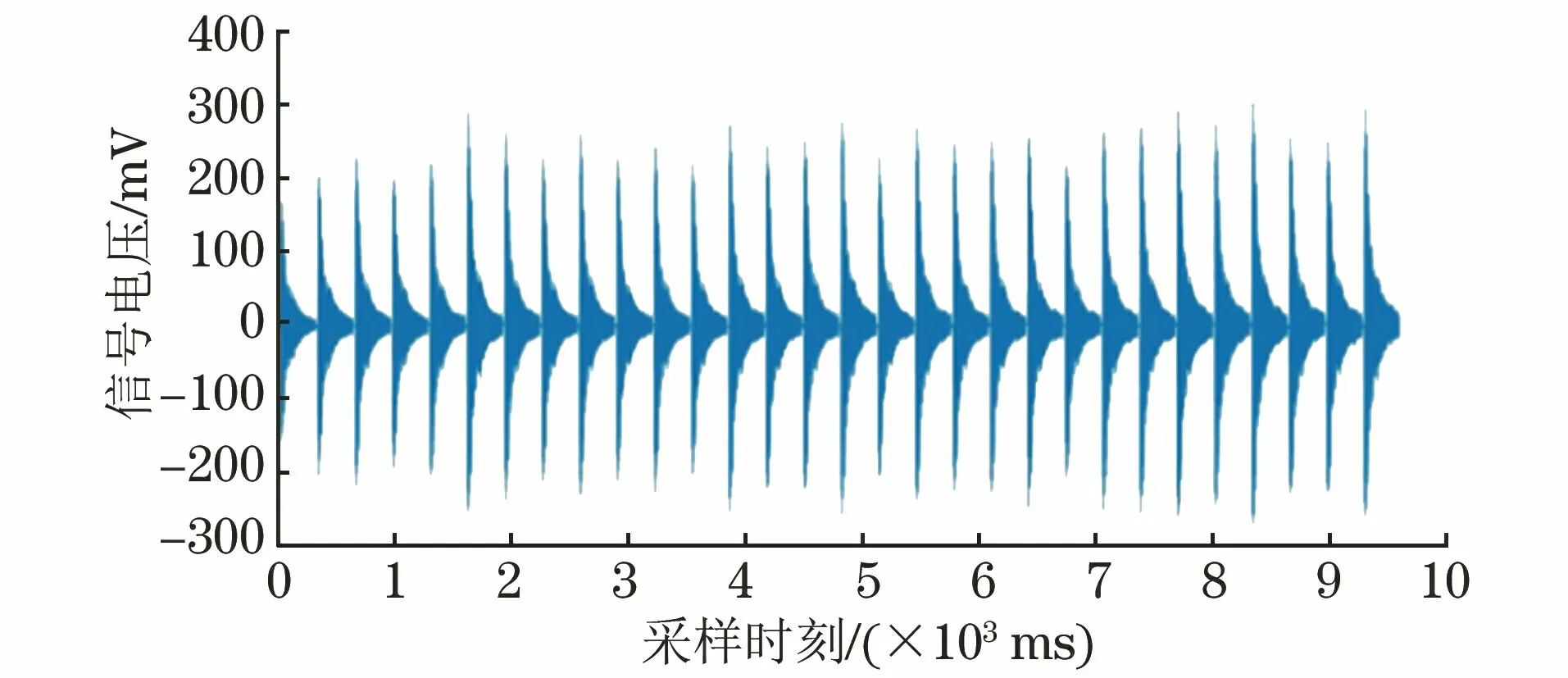
图2 1#试件上采集到的敲击声信号
2.2 敲击信号预处理
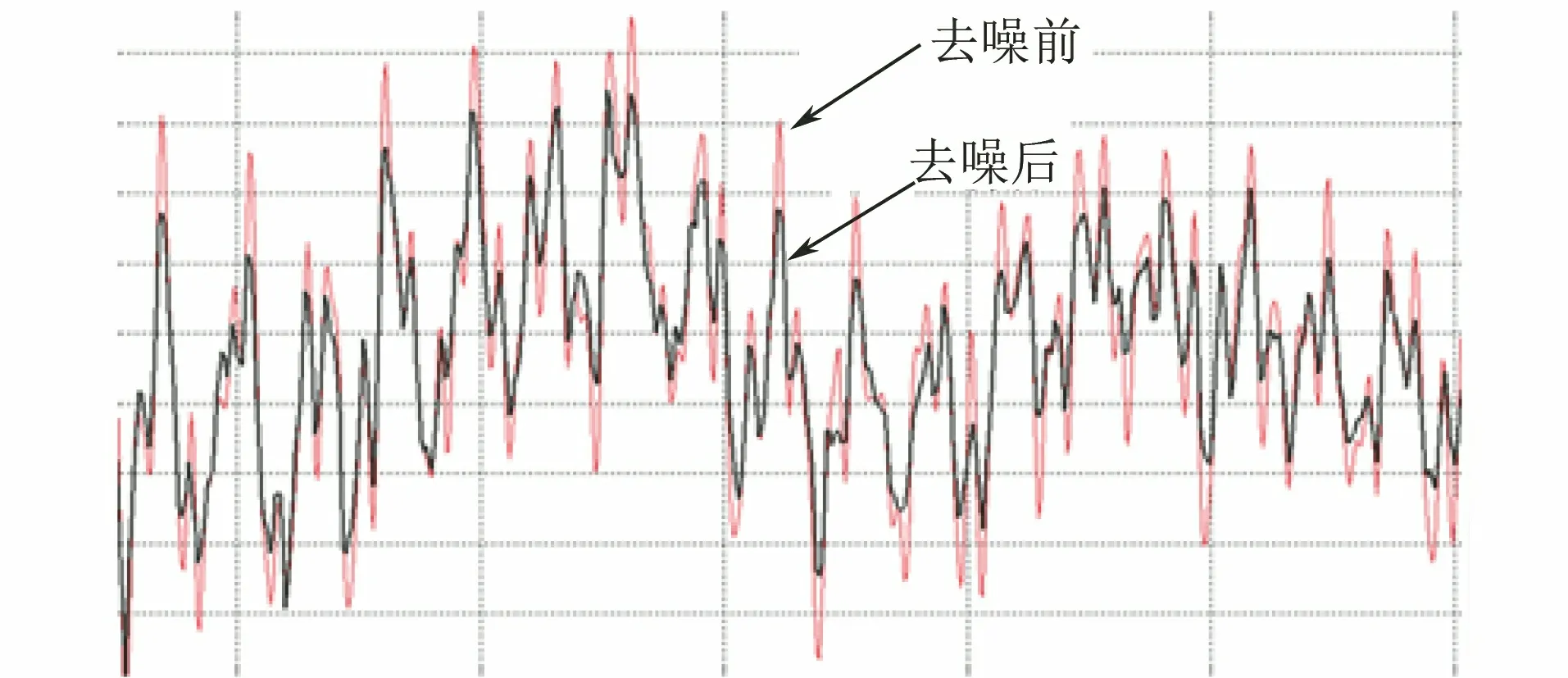
图3 去噪前后的敲击声信号
首先对信号进行“五点三次滑动”滤波,然后用小波包基函数对平滑后的信号进行5层小波包去噪(软阈值为0.05),处理后的信号尖端噪声明显降低,且没有明显的相位和波形畸变(见图3);最后采用最大值法对去噪后的信号进行标准化。采用状态机法根据短时能量、短时过零率、最小等待长度等参数综合判断各帧所处的状态(敲击等待、模糊、敲击进行、敲击结束),并把敲击信号分割成单独的信号段[14]。分割后的信号段长度稍有差别,为了方便后续信号处理,取以上各信号段长度的中值为参考对信号进行分段,分段结果如图4所示。
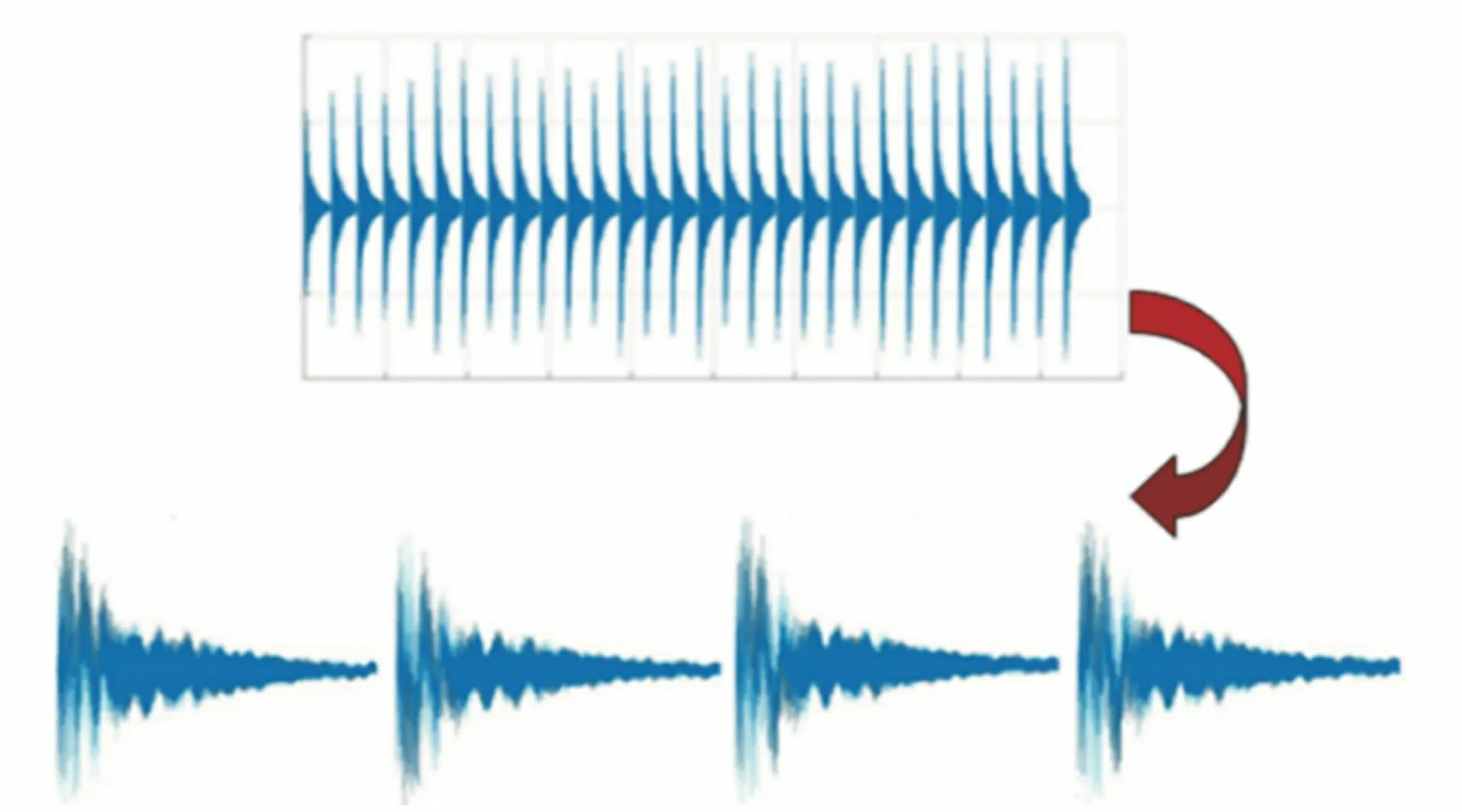
图4 敲击声信号的分段结果
3 敲击信号的频谱分析
3.1 构件缺陷与敲击声信号的相关性
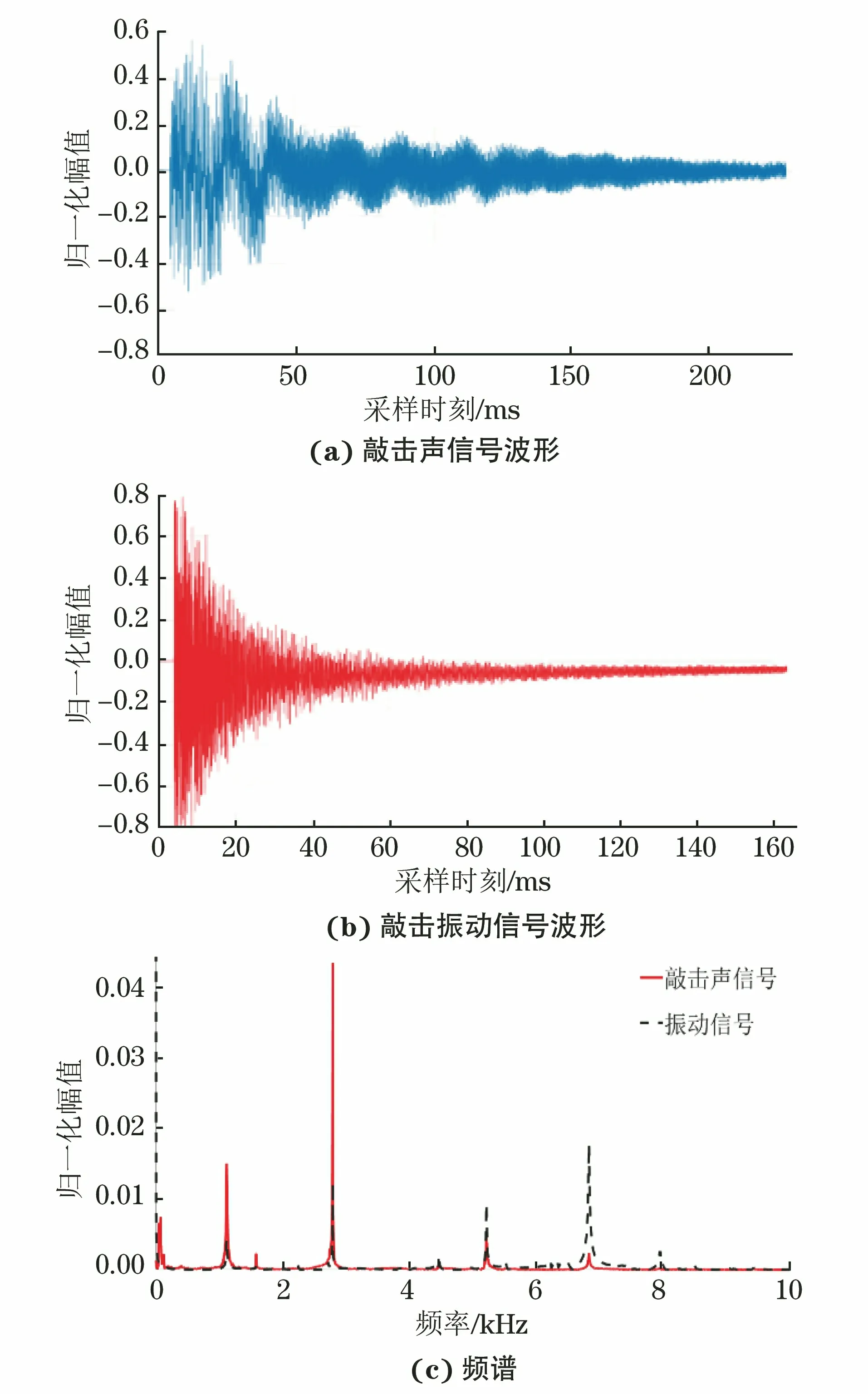
图5 1#试件某次敲击采集到的信号波形及其频谱
图5为1#试件某次敲击采集到的信号波形及频谱,可以看出敲击声信号和敲击振动信号的频率峰出现的位置基本一致。这是因为二者为同源信号,信号特征都是由构件的振动模态和结构特性决定的[15]。图6为敲击力增大时的信号(试件不变),可见该信号与图5的时域波形高度相似且频谱峰重叠,说明了在一定的敲击力度范围内,敲击力的大小对构件的振动模式影响较小。

图6 1#试件敲击力增大时的敲击声信号及频谱

图7 1#~4#试件的敲击声信号频谱
图7为1#~4#试件的敲击声信号频谱,可以看出1#,2#试件的敲击声频率分布高度相似,但4个主要谱峰向低频端偏移了49,36,59,89 Hz,且最高峰位置也发生了转移;3#和4#试件含有开裂和夹层缺陷,其对试件的结构完整性的破坏力度更大,信号频率主峰向低频端偏移的现象更严重,杂散峰数量也明显增多。
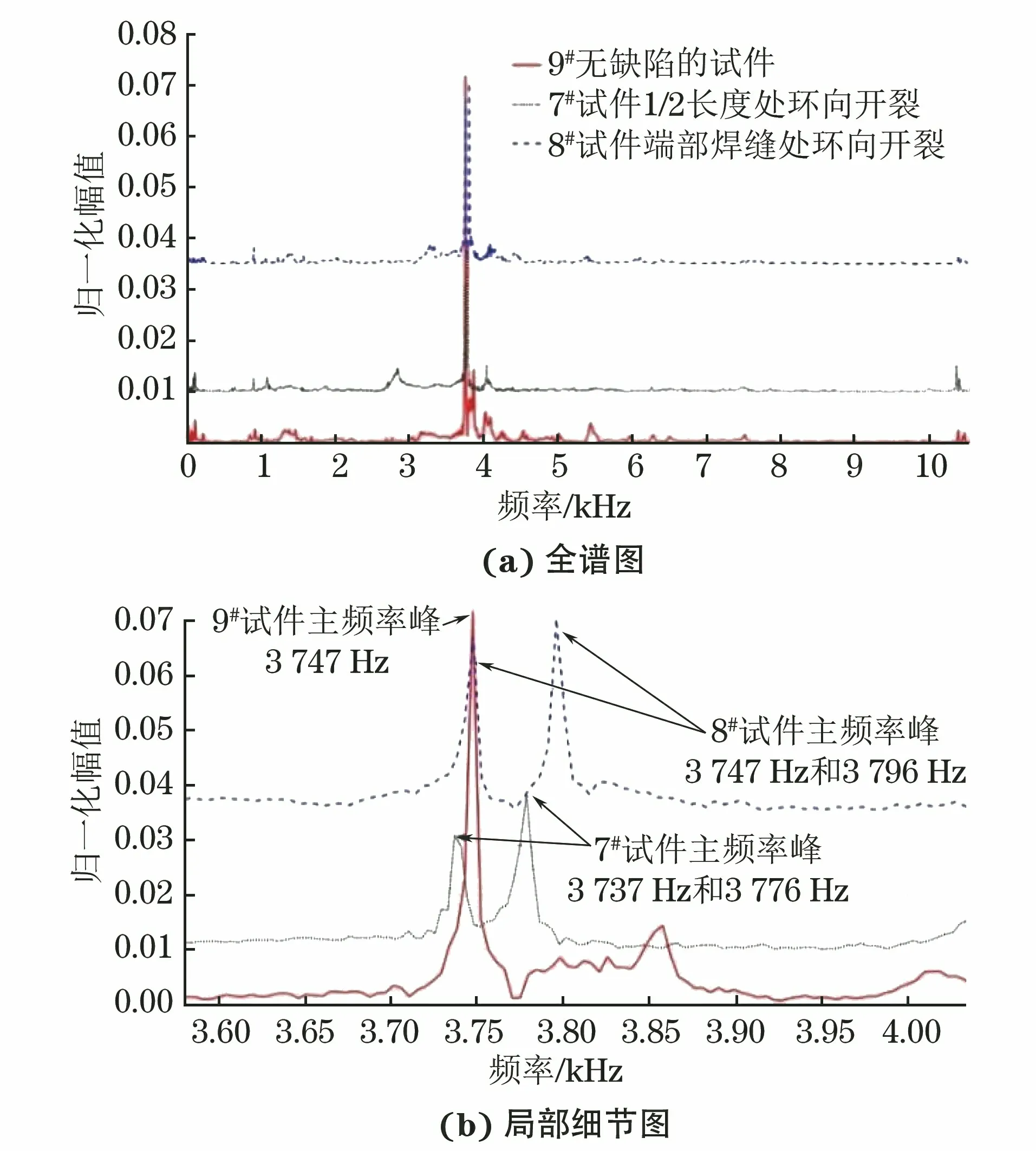
图8 7#9#试件的敲击声信号频谱
图8为7#~9#钢管试件的敲击声信号频谱,其中7#和8#试件的频率幅值分别人为上移了0.01,0.035,可以看出3个试件的频率曲线比较相似,频率峰值集中在3 500~4 000 Hz,从图8(b)的局部细节图可看出无缺陷的9#试件在3 747 Hz处有1个主频率峰,而存在环向裂纹的7#,8#试件在3 747 Hz附近发生了主峰分裂,峰值降低较大,最高峰位置也发生了一定偏移。
上述敲击过程可用图9所示的弹簧模型进行解释[16]。敲击右边完好部位相当于敲击一个弹性系数为kc的弹簧;敲击左边缺陷部位,相当于在右边完好构件的弹簧模型上串联一个弹性系数为kd的弹簧,kd与缺陷深度h,缺陷长度l以及被敲击部位的截面惯性矩等有关。假设局部敲击时系统中运动部分的抽象质量为m,等效弹簧的弹性系数为k,x和分别为局部位移和局部位移加速度,则有
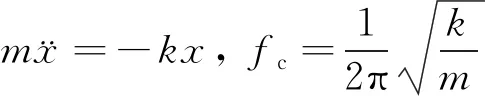
(7)
式中:fc为构件的振动频率。
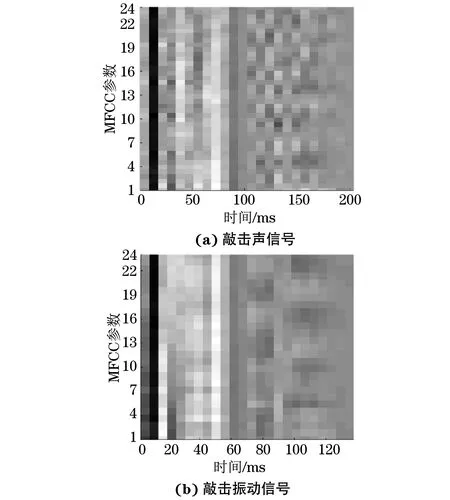
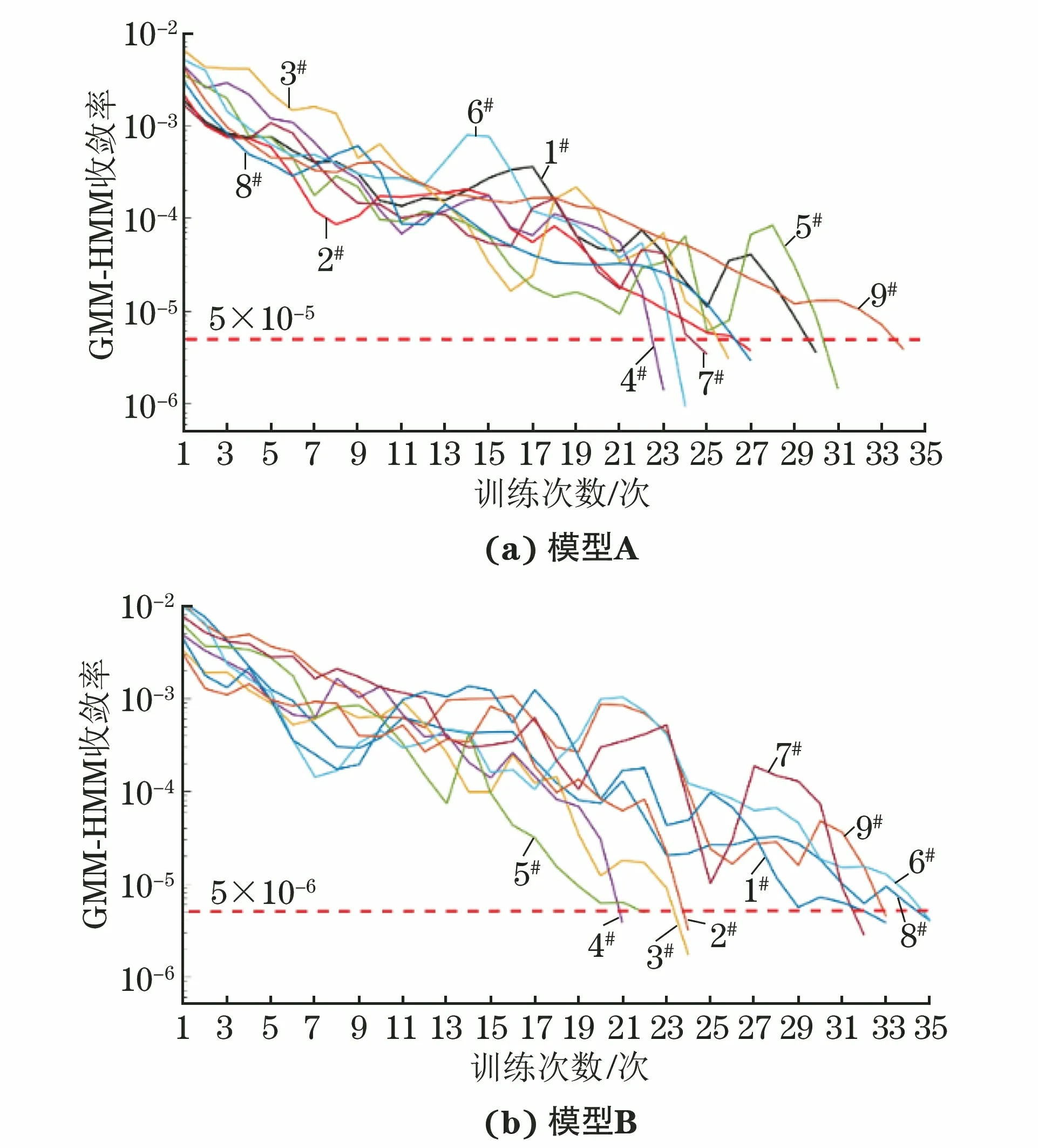
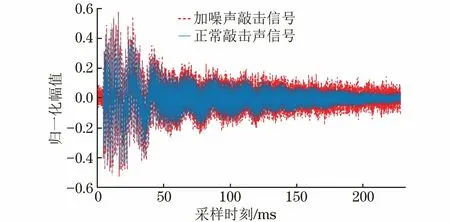
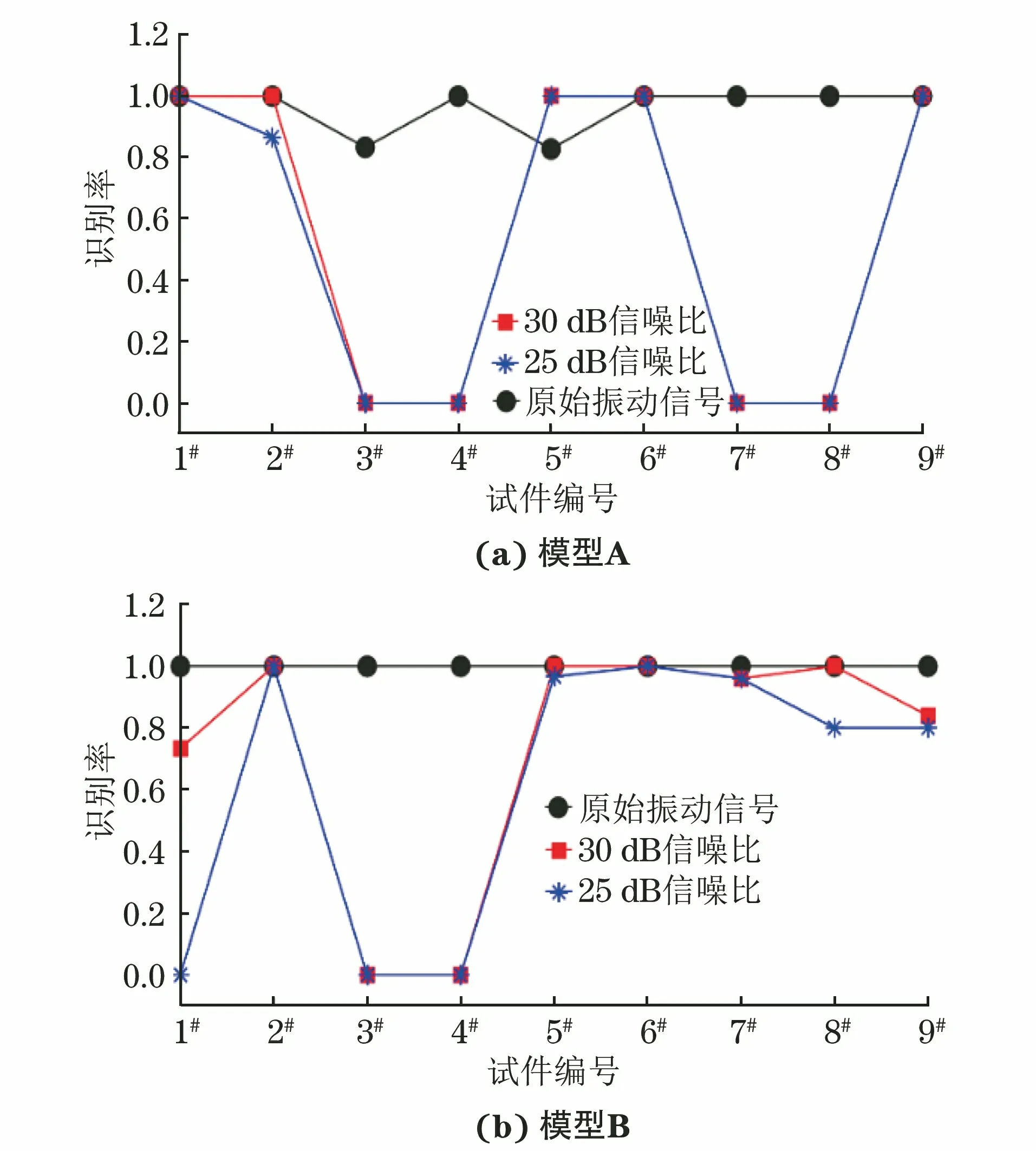
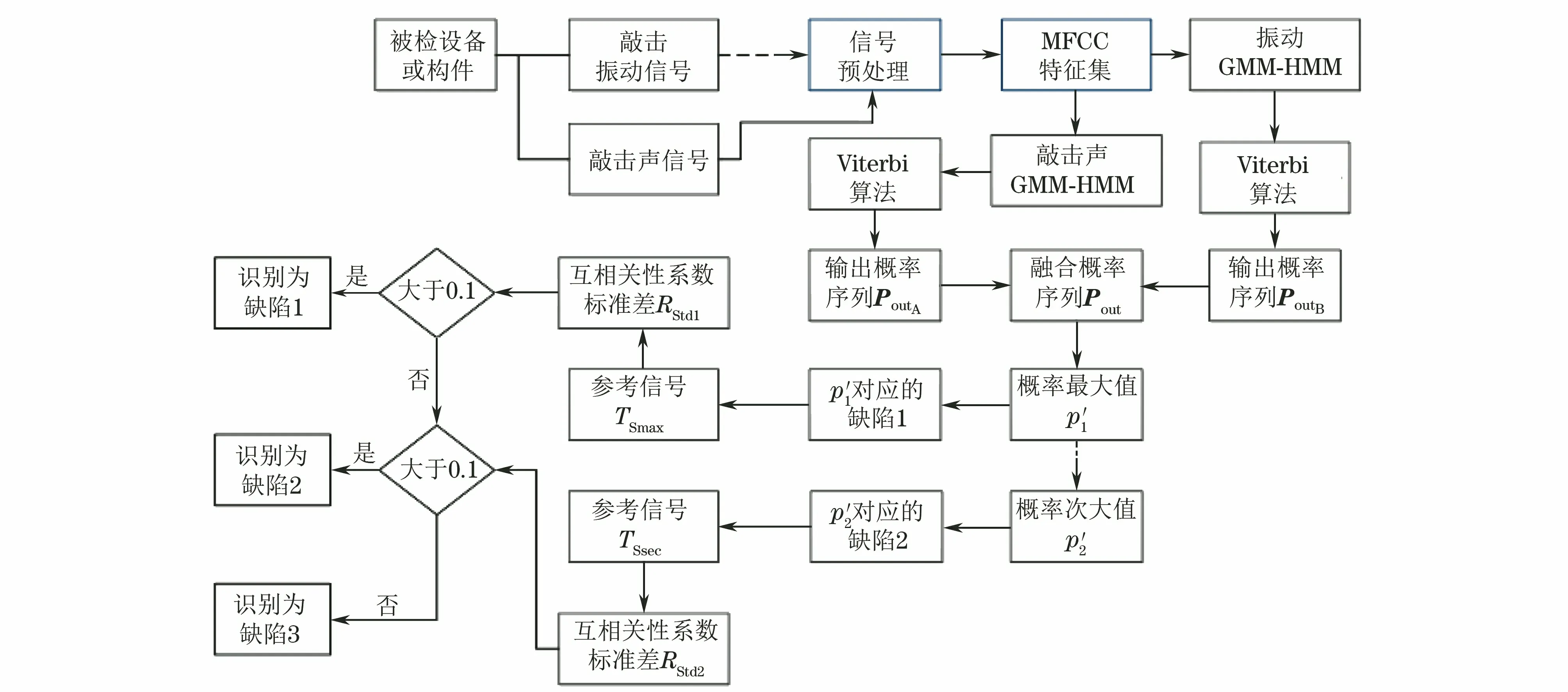
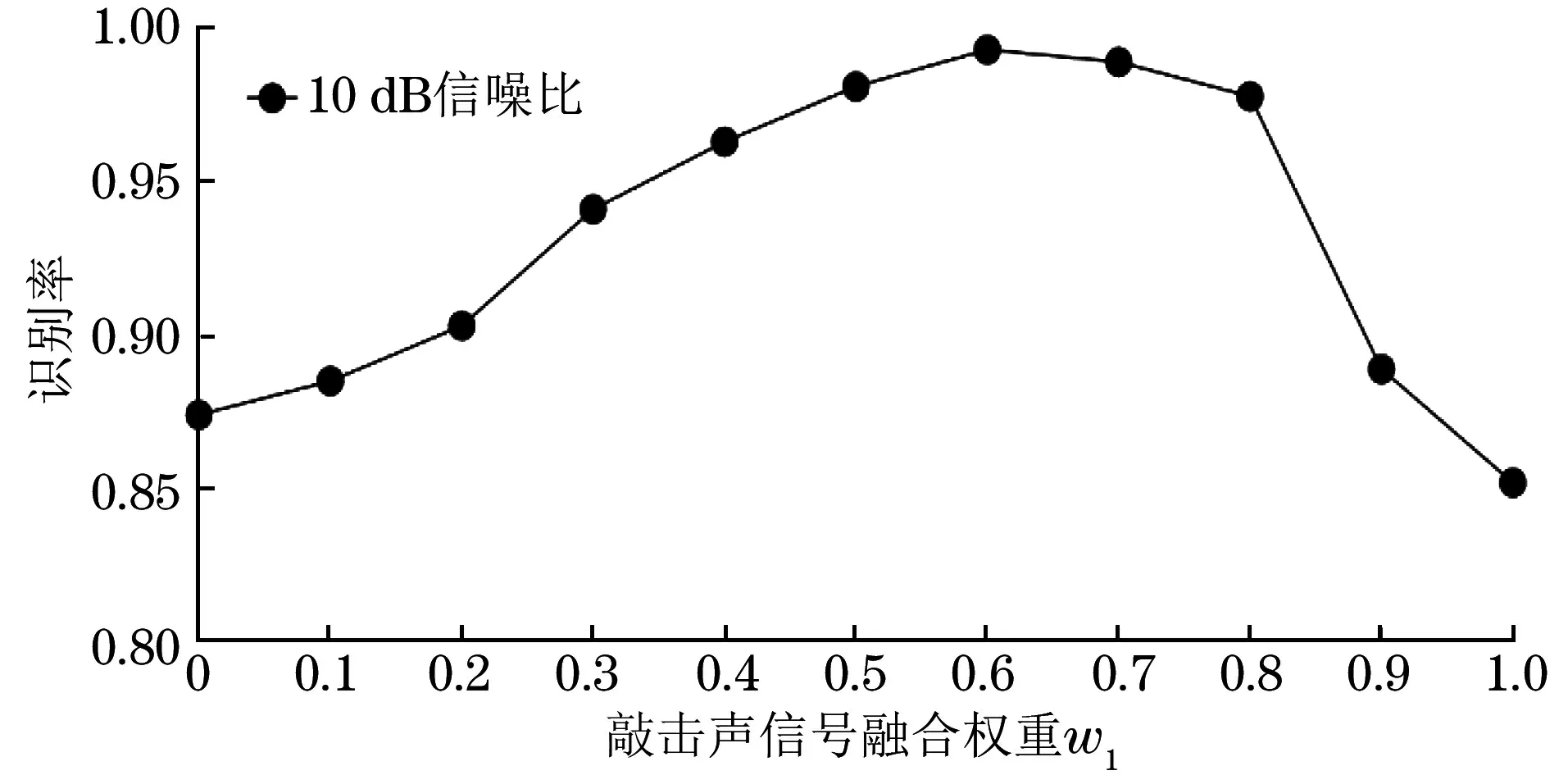
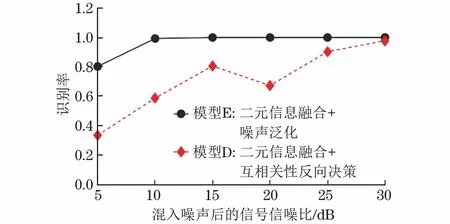
在完好构件部位k=kc,而在缺陷部位k=kc×kd/(kc+kd) 图9 敲击检测的弹簧模型 薄壁钢管的敲击检测模型如图10所示。环向裂纹处相当于一个长度为0的自由面,瞬时敲击振动波UI沿着管壁传播,遇到裂纹面时会产生反射波UR与透射波UT。假设裂纹的等效面积为Sc,无损伤处的管壁面积为S0,当忽略相位变化时,UR和UT有以下近似关系 UR(0,ω)=CUI(0,ω) (8) UT(0,ω)=KUI(0,ω) (9) 式中:ω为振动波的角频率;C,K为与Sc/S0有关的常数项。 图10 薄壁钢管的敲击检测模型 根据能量守恒关系有 (10) 由式(8)(10)可知,当薄壁直管段上存在环向裂纹时,振动波的传播不可避免地被裂纹自由面所影响,管段上的振动波也以裂纹面为界分为不同的两部分,这也是图8中7#,8#试件在3 747 Hz频率处发生谱峰分裂的原因。 互相关分析可以用来衡量两个周期信号随时间变化时的相关性,图11为敲击信号的互相关系数Rxy(m)曲线(m=1, 2, 3,…,3 000,为信号的采样延迟数),可以看出Rxy在零点上下呈周期性振荡,但同类试件敲击信号Rxy曲线的标准差要远大于不同类试件Rxy曲线的标准差,该特性可以用来验证两种信号是否源自同一类别。 图11 敲击信号的互相关分析 在语音识别方面,最常用到的语音特征就是梅尔频率倒谱系数(MFCC),其可描述人耳频率的非线性特性[17]。敲击信号经预加重、分帧、傅里叶功率谱提取、24维度三角梅尔滤波器组滤波和离散余弦变换后得到梅尔系数,舍弃后12维系数并用前12维系数的一阶差分替换,最终得到24维的MFCC参数,MFCC参数的灰度映射图如图12所示。 图12 MFCC参数的灰度映射图 敲击样本分为训练和测试两个样本集,每个试件的训练样本子集包含80~100个样本,测试集大小约为训练集的1/4,GMM-HMM模型包括9个与试件类别相对应的子模型,隐藏状态数为6,其发射概率由m个高斯子分布函数决定,主要参数可由K-mean等聚类算法得到,文章在参数初始化时引入Calinski-Harabasz 指标对不同m值的聚类效果进行评价,选取最优的m值。采用EM算法进行训练,当收敛率小于5×10-6时停止训练,图13为分别利用敲击声信号得到的模型A和利用敲击振动信号得到的模型B的收敛率曲线,图中纵坐标为对数收敛率。 图13 GMM-HMM训练时不同模型的收敛率曲线 在无噪声干扰时,模型A和B的识别率分别为96.3%,100%,表现出良好的识别效果。在测试信号上混入一定强度的高斯白噪声(见图14),混入噪声后的信噪比为30 dB(假设原始信号中不含噪声),此时模型A和B的识别率分别为57.4%,72.1%;在信噪比为25 dB时,则为54.8%,61.0%,识别率随着噪声增大而急剧降低。图15为模型A和B对9类试件的识别率,在噪声环境下,模型A不能正确识别3#,4#,7#,8#试件,模型B不能正确识别1#,3#和4#试件。 图14 混入高斯白噪声前后的敲击声信号 图15 GMM-HMM对不同类别试件的识别率 图16 “二元信息融合+互相关性反向决策”算法流程图 4.2.1 二元信息融合+互相关性反向决策 为了提高GMM-HMM的鲁棒性,采用 “二元信息融合+互相关性反向决策” 算法对其进行改进,改进流程图如图16所示。主要步骤为:① 提取敲击声信号T1,T2,…,T9作为参考信号;② 计算总概率序列Pout=PoutA×w1+PoutB×w2,PoutA,PoutB为模型A,B的输出概率序列,敲击声信号权重系数w1、振动信号权重系数w2均为0.5;③ 利用“互相关性反向决策”算法对概率序列Pout中排在前3位的输出值进行校验和重新排序。在30 dB和25 dB的信噪比下,采用“二元信息融合”算法(模型C)对信号进行识别得到的识别率分别为87.4%,80.0%; 采用“二元信息融合+互相关性反向决策”算法(模型D)对信号进行识别,得到的识别率则为97.8%,90.4%,优于模型C的。与采用单一信息的模型A、 B相比,模型D综合了敲击声和敲击振动信息,又利用“互相关性反向决策”对识别结果进行校验,进一步提高了识别率。 4.2.2 二元信息融合+噪声泛化 在10 dB信噪比的噪声环境下,模型D的识别率仅为58.9%,已不能满足工程需求。在深度学习中常采用噪声泛化来提高训练集的多样性[18],文章采用类似的方法在初始训练集中混入一定强度的高斯白噪声(10~30 dB的随机信噪比),然后和初始训练集共同组成新的训练集。图17为采用“二元信息融合+噪声泛化”算法的模型在不同信号融合权重时的识别率,横坐标最大值1表示只使用敲击声信号进行识别。从图17可以看出,当w1=0.6时,模型的识别率最高,此时,记该模型为模型E。此外,由于添加噪声的影响,模型E再融合“互相关性反向决策”算法并不能进一步提高识别率,甚至还会降低识别率。 图17 “二元信息融合+噪声泛化”模型在不同信号融合权重时的识别率 图18为模型E和D在不同信噪比下的识别率,可见模型E的识别率明显优于模型D的,其在10,5 dB信噪比时的识别率分别为99.3%,80.4%,表现出较强的鲁棒性。进一步地,模型E与参考文献[19]建立的20层卷积神经网络模型(CNN)进行对比,在信噪比为10 dB时模型E的识别率要优于基于敲击振动信号的CNN模型(98.2%)的识别率,稍低于基于敲击声信号的CNN模型(100%)的,但文章所构建模型的可解释性要优于CNN模型的,而且对硬件设备的要求也相对较低,更适合工程应用。 图18 模型E和D在不同信噪比下的识别率 (1) 在局部敲击激励下,金属部件的敲击信息与被敲击部位的结构完整性密切相关,特定的频域特征峰对应着特定的缺陷形式;缺陷的存在会导致敲击信号的频谱向低频段移动或频率主峰发生分裂,通过互相关系数分析可以验证两种信号是否源自同一类别的缺陷。 (2) 利用敲击声和敲击振动信号的MFCC特征参数构建的GMM-HMM模型可以有效识别出不同的缺陷试件,但识别结果易受到噪声影响。 (3) 经“二元信息融合+噪声泛化”算法改进后的GMM-HMM模型在敲击声信号融合权重为0.6时,识别率达到最优,在信噪比为10 dB时的识别率为99.3%,相关算法模型可用于特种设备金属部件内部缺陷的快速敲击识别及其他智能化无损检测领域。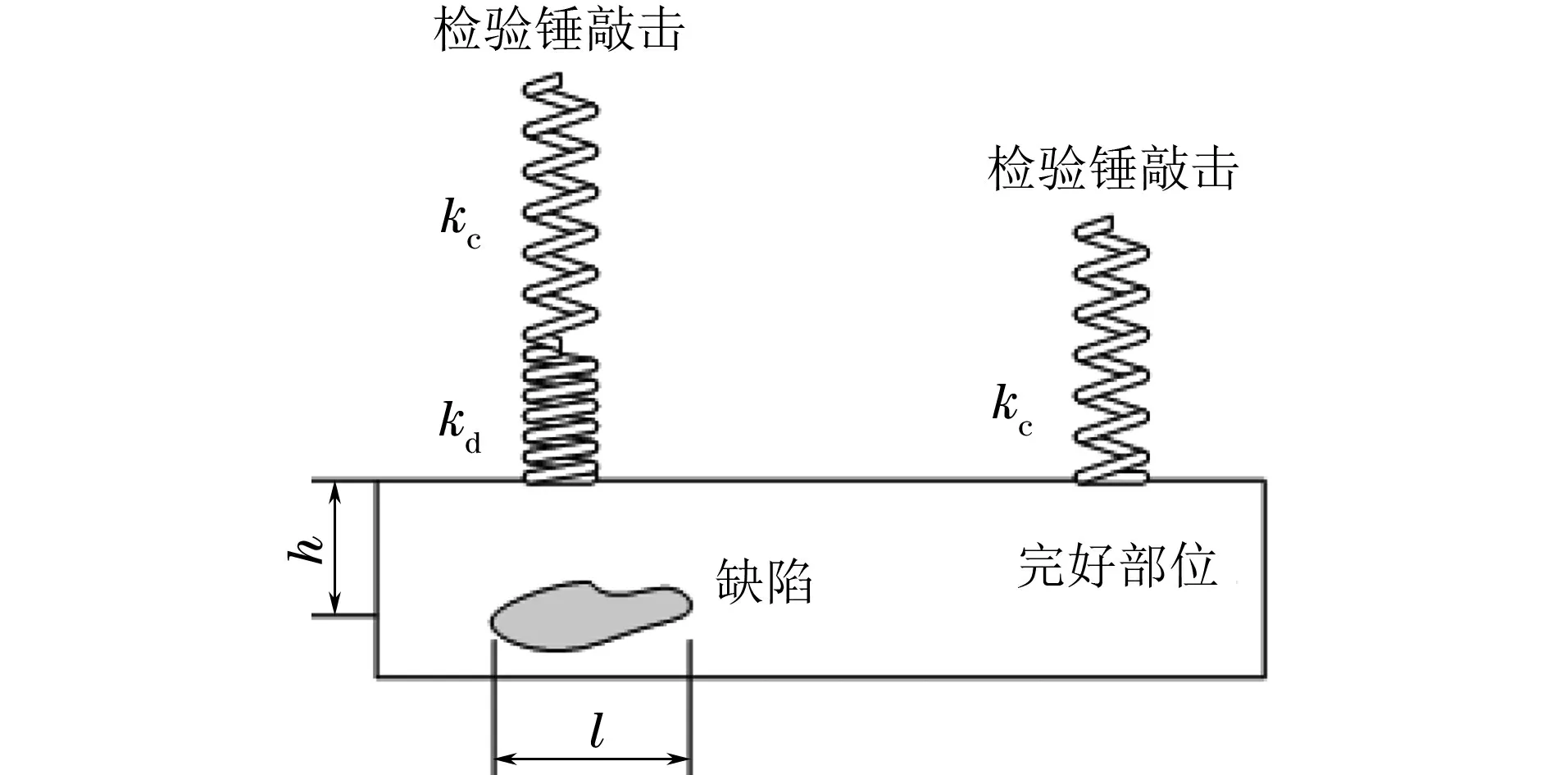

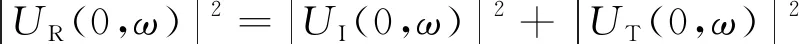
3.2 敲击信号的互相关分析

3.3 MFCC特征集
4 缺陷识别模型搭建与试验结果分析
4.1 GMM-HMM模型搭建
4.2 GMM-HMM模型改进
5 结论

