一阶线性变系数对流方程的稳定性分析

张甜甜，许文文，郭红，杜明洋，余昌彪

(齐鲁工业大学(山东省科学院) 数学与统计学院，山东 济南 250301)

变系数对流扩散方程对研究自然界和实际工程中的很多物理现象具有重要意义，且在众多学科中的应用极其广泛，如流体力学、气体力学等[1-2]。在研究此类问题时，扩散项的计算相对简单，对流方程的计算通常是研究重点。

一阶变系数对流方程在自然科学领域的应用背景较广泛。王国栋等[3]将迎风格式应用到一阶变系数对流方程的推广模型交通流中，并通过新的格式模拟相关实例；Chen 等[4]通过耗散谱方法求解一阶变系数双曲方程(对流方程是最简单的双曲方程)，通过傅里叶耗散谱方法讨论周期问题，通过Legendre耗散谱方法讨论边界问题，且列出严格的误差估计式； Aguirre等[5]在以Hermit函数为正交基的Herbert空间里开展对一阶变系数双曲方程周期边界问题的研究，通过理论分析给出了收敛阶 。关于对流方程的传统数值解差分格式有迎风格式、Lax-Friedrichs格式、Lax-Wendroff格式、Beam-Warming格式和蛙跳格式。其中，迎风格式的基本思想是用向前差商或向后差商来代替空间偏导数，其关于时间和空间都是一阶的，且是条件稳定的，算法在计算机上便于实现，因此在实际计算中受到广泛重视，并得到了一些好的方法和技巧。本文我们将采用迎风格式逼近一阶变系数对流方程并探索格式的稳定性条件[6-9]。

常系数问题差分格式的稳定性分析一般采用傅里叶方法和直接方法[9-11]，但是变系数问题的稳定性分析相对复杂，通常不采用上述两种方法，目前国内外关于一阶变系数对流方程稳定性的相关研究较少。对于变系数方程差分格式稳定性问题，能量不等式方法是一个严格且很有技巧的方法。用能量不等式方法讨论差分格式稳定性是从稳定性的定义出发，通过一系列估计式完成的，这个方法是偏微分方程中常用的能量方法的离散模拟[9]。本文将采用能量不等式方法分析一阶变系数对流方程迎风格式的稳定性条件，分别就变系数的正负取值情况并结合冻结系数法验证网格比条件，进而推导出稳定性条件，最后进行数值模拟验证理论分析的正确性。

1 一阶线性变系数对流方程初值问题

对于简单的一阶线性变系数对流方程的初值问题:

(1.1)

如果a(x,t)对x和t都是一次连续可微的，那么a(x,t)光滑变化，与常系数情形类似，(1.1)式的特征线满足的方程为：

(1.2)

令x=x(t,x0)和u(x,t)分别是方程(1.1)和方程(1.2)的解，则：

(1.3)

于是，方程(1.1)的解沿特征线为常数。此时特征线为曲线，且有：

u(x,t)=u0(x),x=x(t,x0)。

(1.4)

因此，我们将已学常系数方程推导的差分格式推广到变系数方程(1.1)。

2 迎风格式

设初值问题(1.1)的解区域为[0,l]×[0,T]，将此区域沿x轴和t轴方向进行矩形网格剖分，其中空间步长为Δx=h=l/J，时间步长为Δt=τ，网格点记为(xj,tn)，网格线可写作:

xj=jΔx=jh,j=0,1,2,…,J，

tn=nΔt=nτ,n=0,1,2,…。

由于变系数对流方程(1.1)的迎风差分格式是对流方程关于空间偏导数用在特征线方向一侧的单边差商来代替的，且其系数a(x,t)符号是变化的，因此迎风格式可以写成如下两种形式：

(2.1)

(2.2)

|λj(G(τ,k))|≤1+Mτ,j=1,2,…,p，

其中|λj(G(τ,k))|表示增广矩阵G(τ,k)的特征值，M为常数[9]。此条件称为von Neumann条件。

3 稳定性分析

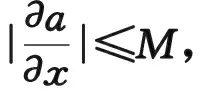
(3.1)

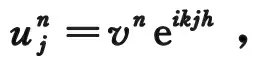
vn+1eikjh=vneikjh-aλ(vneikjh-vneik(j-1)h)，

(3.2)

两边同时消去公因子eikjh得：

vn+1=vn[1-aλ(1-e-ikh)]，

(3.3)

所以增长因子为：

(3.4)

则有

|G(τ,k)|2=[1-aλ(1-coskh)]2+a2λ2sin2kh

(3.5)

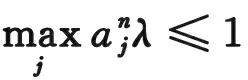
接下来我们分情况讨论迎风格式稳定性：

(3.6)

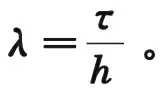
(3.7)

网格比满足条件：

(3.8)

根据基本不等式a2+b2≥2ab并进一步化简有：

用h乘上式两边并对j求和，记离散范数：

(3.9)

那么有：

(3.10)

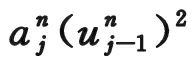
(3.11)

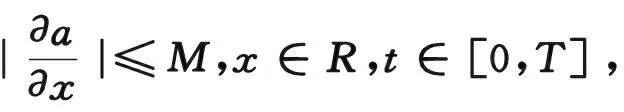
(3.12)

从而有

(3.13)

重复使用上式有：

(3.14)

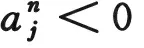
(3.15)

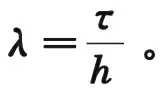
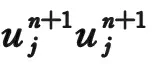
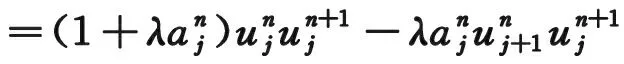
同理可知网格比满足如下条件：

(3.16)

根据基本不等式a2+b2≥2ab并进一步化简有：

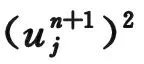
用h乘上式两边并对j求和，记离散范数：

(3.17)

那么有：

(3.18)

(3.19)

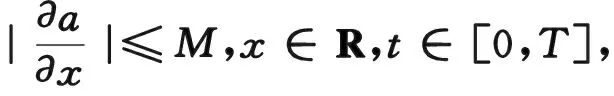
(3.20)

从而有

(3.21)

重复使用上式有：

(3.22)

4 数值算例

现在通过一个简单的数值例子验证用能量不等式的方法分析变系数对流方程的初值问题的迎风格式的稳定性条件。

对于初值问题：

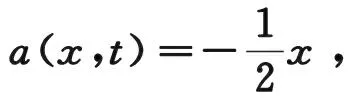
u(x,t)=x2et。

(4.1)

取空间步长h=0.01, 时间步长τ=0.01，则λ=1，将迎风格式计算到tn=0.1时，计算得到初值问题的迎风格式的数值解与解析解，然后将数值解与解析解进行对比判断此初值问题的稳定性，参考文献[12]，对随机选取的部分输出结果进行对比，见表1。

表1 数值解与解析解

从表中数据可知，迎风格式的数值解与解析解的误差很小，即可认为此初值问题是稳定的。

图1和图2为输出迎风格式的数值解图像与解析解图像，x轴代表空间方向的长度，y轴代表时间方向的长度，图1的z轴是所研究初值问题的迎风格式关于x轴和y轴的数值解u(x,t)，图2中的z轴是所研究初值问题关于x轴和y轴的解析解z(x,t)。从迎风格式的数值解与解析解图像可以直观地看出此初值问题的迎风格式是稳定的。

图1 迎风格式数值解Fig.1 Upwind scheme numerical solution

图2 解析解Fig.2 Analytical solution

5 结语

本文采用迎风格式逼近变系数对流方程，然后通过冻结系数法求出一阶变系数对流方程的迎风格式稳定需要满足的网格比条件。再对其迎风差分格式通过能量不等式的方法并结合冻结系数法得出的网格比条件进行讨论得出其稳定性条件。最后通过一个数值算例对比其解析解与数值解，验证稳定性条件的正确性。