算思并行:运算单元整体教学的思考与策略
文|徐丹红 徐晓良
细研《数学课程标准(2011年版)》,我们发现从计算能力到运算能力,不只是换了名称,而是从核心素养的高度进行了重新定位,内涵和外延都发生了变化:运算能力不等同于“计算能力”,不再是单纯的“能计算”“会计算”。运算能力是一种综合能力的体现,是运算技能与逻辑思维能力等的一种独特的结合。其主要的表现是:正确运算、理解算理、方法合理。也就是说能正确计算只是运算能力培养的基础,同时要理解计算过程中方法后面隐含的算理,最终达到能灵活选择计算策略解决问题的目的,所以运算能力也是一种高阶能力。
一、以测观能:学生运算能力现状分析
通过对四年级学生运算能力的测试,发现学生单项计算类题型正确率较高,基本算法和算理掌握得较好。但当计算与其他知识融合进行综合考查时,正确率就明显下降。问题主要集中在以下几个方面:一是数据敏感程度较低:只计算不观察,无数据分析意识。二是算理深度理解不够:知技能不明理,无深度理解能力。三是算法灵活选择缺乏:无要求不选择,无策略选择习惯。四是运算综合能力薄弱:单计算不相联,无沟通运用思维。
二、以生思行:教师运算教学问题思考
1.计算教学“独立化”,不利于学生理解能力和选择能力的培养。
无论是整数、小数还是分数的运算教学,教材均将其清晰地分为口算、估算、笔算、简算进行独立编排,以便让学生清晰地掌握每一板块的知识。但教材的独立编排并不意味着教学也是独立的,特别是面对学生单一能力强、综合能力弱的情况,教师更应做到知识间的融通。
2.难度设置“小步化”,不利于学生迁移能力和推理能力的形成。
通过课堂我们发现:运算教学中教师将知识点分解太细,难度设置太小步化。这样于一节课的教学而言,容易出现思维的断层,学生难以形成整体性思考;于单元教学内容而言,分割细、课时多,容易形成枯燥、乏味、课与课之间缺乏沟通和联系的情况,使得学生迁移、推理能力的形成难度较高。
3.教学目标“单一化”,不利于学生观察能力和分析能力的养成。
由于教师对运算能力的理解单一,在设计运算内容的教学时,常常只将“能算、会算”作为教学的单一目标,忽视了数据的观察、分析能力,影响了学生依据数据分析选择算法等一系列能力的养成。
4.练习设计“固定化”,不利于学生综合运用能力的提升。
练习设计形式固化,口算、笔算、递等式计算……各项练习均有明确的题目要求,“根据题目要求选择方法”而不是“根据实际需求选择方法”。练习设计内容固化,不能通过一道练习联系起学生多方面的知识与能力。将“正确计算”作为运算练习的主要指标,而没有将练习的过程进行综合评价,不利于学生综合运用能力的提升。
三、以问拟策:算思并行的单元整体教学
史宁中教授提出运算教学的过程也是推理能力不断形成的过程。其实,运算的教学不可能、也不应该只是单一的“算”的过程,而同时也应该是“思”的过程。从单元视角整体把握教学,将运算思维能力的培养融合于每一节课、每一次运算中,以达到计算技能和思维能力培养的双赢,真正提升学生的运算能力。
1.理法融通,整体架构教学内容,凸显运算本质。
熟练基本口算、掌握算法、理解算理,才能灵活选择运算的策略。深刻算理理解是熟练掌握算法的基础,灵活选择算法的保障,以理入法,才能更好掌握运算的本质。那么,如何在教学中让“理”更深入,“法”更灵活,理法融通,进而提升运算思维能力呢?
(1)种子课,建立整体感知。
运算教学与其他教学内容一样,并不是散点式的存在,内在的融通、整体的感知是沟通理法、灵活运算、提升能力的前提。如《有余数的除法》是表内除法与除数是两位数的除法的承接课,一是完善表内除法中的认知结构;二是为除数是两位数的除法打基础。以下是《有余数除法》的教学内容安排:

例题具体内容例1余数及有余数的除法的含义例2余数和除数的关系例3有余数的除法竖式和表内除法的竖式例4试商例5解决简单生活问题,并用“进一法”确定答案例6解决与按规律排列有关的问题
在本单元的教学中,从例1 至例3,教材都是以“提供直观图,圈一圈”的形式呈现,所以学生的学习会遇到两大难题:一是竖式的学习,余数的得出都可以通过“圈”而获得,那么对于竖式本身的作用以及竖式中“商与除数的乘积”的含义理解就存在困难;二是试商,前面的教学只有“圈”出商和余数,试商自然也就存在困难。因此,我们整合单元教学内容,确定了第一课时的教学内容:在“正好分完”和“有剩余”的对比中认识余数和有余数除法;在“分物中怎么知道余几”的问题探寻中知道可以借助画图法,也可以采用口诀法;在口诀法中渗透试商,并初步引出竖式的表征。
在这样的整体架构中,让学生感知到:分物可能分完,也可能有剩余。找到余几可以实际操作分一分,也可以借助前面的乘法口诀帮助寻找。而借助口诀法虽快但表征麻烦,因此产生了竖式。作为单元的起始课,为整个单元所学的新知进行了整体的铺垫,打通了知识学习的脉络,增强了后续知识学习的驱动性。
(2)疑难课,逐步渗透算理。
无论是算法还是算理的教学,大多数教师的重心都放在了笔算教学中,而笔算的教学更多的是要依赖口算算理的学习,它是口算过程的记录和体现。所以笔者认为算理的理解更应该从口算开始,重视、加强口算算理,逐步渗透、分解算理的难点,为笔算做好扎实的铺垫。
如《除数是一位数的除法》前5 节课的内容安排如下表:

口算除法内容具体安排例1:一位数除整十、整百、整千数例2:一位数除几百几十(几千几百)例3:一位数除两位数(每一位都能除尽)被除数是两位数的笔算除法例1:首位能除尽例2:首位不能除尽、验算
笔算除法例1、例2 是本单元教学过程中的一个难点,学生的难点有二:一是格式上的难,第一次出现商是两位数的笔算除法,学生往往一次性得到结果;二是算理上的难,能算出结果但没有清晰的算理,也不能将算理和笔算过程较好地进行匹配。前面虽已完成口算除法例1~例3 的教学,但没有为笔算做好足够的铺垫。因而在整合前面3 道口算例题教学之后,我们新增加了“口算42÷3”的教学。
笔算的算理不是随着笔算的产生而产生的,始于口算,直观体现于笔算。将算理的教学前置于口算教学中,可以分散难点,能更“集中精力”理解算理,逐步渗透和强化算理。
(3)算理课,强化多元表征。
三年级下册《口算除法》片断:
例1:把60 张彩色手工纸平均分给3 人,每人得到多少张?
列式解决说算法。绝大多数学生的计算方法都是60÷3,先不看60 后面的0,计算6÷3=2,再在结果中补上0。但为什么这样算很少有学生能说清,于是将问题集中到:为什么“0”可以不看?你能不能用自己的方式说明理由。
生3:把60 张看成6 个十÷3=2 个十,就是20。
在学生表征的基础上,教师顺势引导:无论上面哪种方式,我们都把60 看成了6 个十。
6÷3=2,6(个十)÷3=2(个十),利用6()÷3=2()还能计算哪些题?
用多种方式表征算理,将说不清道不明的算理直观地呈现在学生面前,不仅能更清晰地理解算理,同时以一题推一类,建立了整十数、整百数……除以一位数的模型。
其实算理的表征方式有多种,如以12×14 为例:
算式表征:“10 个14”+“2 个14”。
基于学生的认知水平,鼓励学生用多元的方式表征数学知识。不同的表征带给学生不同的感官刺激,借用多种表征,调动学生多感官参与,在讲清算理的同时也让算理的表象更深刻。
(4)算法课,放慢优化脚步。
算法的多样化与优化是计算教学的一部分,算法的优化不仅是技能的熟练与提升,同时也是算理强化的过程。但是很多课堂教学在做优化时过于着急和匆忙,如笔算两位数乘两位数14×12 的教学:

我们的教学需要算法的优化过程,在对比中优化,在优化中提升。但算法的优化是要在学生具有一定体验的基础上进行的,否则很容易演变成对优化方法的机械记忆和产生“优化方法不理解、自己方法不敢用”的现象。
放慢算法的优化过程,不是提倡不优化,而是为优化做更充分的体验和铺垫,给学生细细领悟算理的一个过程,让学生明白优化背后的缘由。
2.算思并举,基于目标设计练习,提升运算能力。
运算能力的提升,练习是必不可少的一个环节。设计带有不同功能和形式的运算练习,并且以练习形式的改变助推教师评价方式的改变,进而达到以练习助推学生运算思维能力提升的目的。
(1)设计专项性练习,培养数据观察意识。
整体观察数据的意识是能灵活选择计算策略的基础,仅凭教师的“先观察、后计算”口号是不够的,需要设计专项性的练习来“迫使”学生进行数据的观察。
如在四年级学习了运算定律后设计这样的练习:
选择两个或两个以上的数组成能简便计算的式子(至少写两个)。
59 1200 8 41 25
在五年级学习了小数乘除法后设计这样的练习:
如下图,第一块地和第二块地的面积之和,比第三块地大多少平方米?

在六年级综合练习中设计这样的限时口算练习:
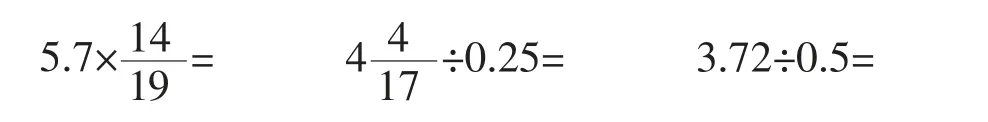
四年级从做简便计算到写能简算的式子,除了考查学生运算定律的掌握情况外,更需要学生专注于数据本身,观察数据的特点;五年级在对比中发现不先观察数据只能“傻傻地算”;六年级在限时口算中感受到观察数据在计算中的重要性。这样的数据观察的“专项性练习”,可以逐步改变学生由“拿到就算”向“先看后算”转换。
(2)设计引导性练习,培养估算策略意识。
估算一方面应用于生活,以简单解决生活中不需要精确计算的问题;一方面也可应用于数学学习,以纯数学估算解决检验、结果范围等问题。
如二年级学习万以内数的认识后会出现这样的练习:
光明小学一年级有学生612 人,二年级有学生595 人,三年级有407 人,报告厅有1500 个座位。三个年级的学生同时去报告厅,能坐得下吗?
单纯地从数的角度而言612+595+407 估成600+600+400 是非常合理的,但在应用于本题时这样的估算方法是解决不了问题的,所以估算并不是难在方法上。本题需要将三个数都估小,特别是595 估成500,然后再和总数进行比较。明明靠近600 的数根据解决问题的需要却要估成500?估出来的结果与1500 又如何进行比较?这就是估算的“难”。这样的难往往会让学生逃避估算而选择精算。因此需要利用一些“引导性”的练习,让学生不得不进行估算,如:
1○电影院有1100 个座位,光明小学的老师准备带一、二年级的学生去看电影,一年级有600 多人,二年级有500 多人,两个年级的学生同时去,座位够吗?
2○电影院有1300 个座位,光明小学的老师准备带一、二年级的学生去看电影,一年级有600 多人,二年级有500 多人,两个年级的学生同时去,座位够吗?
刚开始仍旧有学生会选择假设一个数进行计算,但在对比引导中发现无论多多少人,第一小题都估小、第二小题都估大就能解决问题。
设置这样引导性的练习,逼迫学生进行估算,在无法精算的情况下体会估算的便捷,学习估算的策略,提高估算的意识。
(3)设计过程性练习,培养灵活应用意识。
在日常的批改作业中,对于计算教师常常会有这样的感觉:简便计算时我们常常会关注计算的过程、简便方法运用是否得当,而对于其余的口算、笔算,教师更多的只是看结果是否正确。结果是重要,但也要关注结果的得出过程。
如二年级学习了表内乘法后设计这样的口算题:
7×5+5=( )×( )= 3+2+1+3=( )×( )=
三年级学习了口算除法后设计这样的题型:
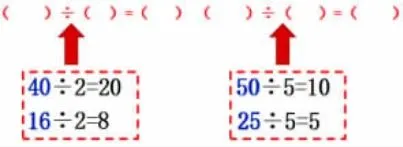
四年级学习了笔算三位数乘两位数后设计这样的练习:
计算“145×67”,数字“4”ד7”表示的实际大小是( )。
A.2.8 B.28 C.280 D.2800
二年级的学生如果能将7×5+5 想成8×5 进行计算,3+2+1+3 想成3×3 进行计算,三年级的学生如果能逆向推算出两步所解决的口算问题,四年级的学生如果能将“4”ד7”的含义清晰表达,都是进一步深入理解算理并在此基础上灵活应用算理的表现。如果只是为了得到上述题目的结果,看看结果是否正确就一批而过,就会与这些精彩的想法失之交臂。
这样“过程性的练习”不以计算结果作为计算教学的唯一标准。善于关注过程、评价过程,也就是更加关注了学生本身、关注了学生的思维,不仅能让教师更多地抓住引导的契机,也能转变学生对于计算“枯燥”“只要算出结果”的想法。
(4)设计多元化练习,培养方法选择意识。
在关注过程性练习、引导性练习的同时,也要改单一指向练习为多元化练习,指向多种方法的选择、指向多种能力的培养……多角度的练习形式,才能给予学生多角度的培养。
在四年级可以设计这样的解决问题练习:
李叔叔的文具店购买24 包新笔记本,成本价是39 元/包,准备800 元够吗?每包12 本,现以每本4 元出售,这批笔记本一共能卖多少元?
第一问是直接利用估算就能解决的,而第二问则需要精确计算。让学生以题目的需求和“哪种方法能更快更好解决问题”为标准选择合适的算法,而不是将“大约”“大概”等字、词作为选择的标准。
让这样的习题变为课堂练习的“常客”,倡导学生去灵活选择,改变计算只是一种技能的观念。有思维了、有挑战了,也就有趣了,学生也就慢慢有了这样自主选择的意识。

