基于流固耦合的浮式拦污排结构优化分析

文善贤，符家和，郭姗姗，杨毅，李思玥，毛汉领*

(1.广西大学 机械工程学院， 广西 南宁 530004；2.南宁交通资产管理有限责任公司， 广西 南宁 530000)

0 引言

浮式拦污排是水电站进水口拦污系统的第一道屏障。水电站进水口前沿设置一道浮式拦污排，可以将进入电站进水口水域表层的大部分漂浮物先行拦截，从而减轻拦污栅和清污机的拦污和清污的压力，避免拦污栅出现严重堵塞问题，保证电站能安全正常运行[1]。由于漂浮物的不断堆积，拦污排所承受的压力越来越大，并且在水流冲击影响下，拦污排承受单向不稳定载荷，造成连接拦污排和支墩的安全拉杆出现疲劳断裂。安全拉杆断裂后，大量漂浮污物涌向拦污栅，导致水电站必须停机清理漂浮物，清理全部漂浮物需要几天甚至十几天，长时间的停机清理给水电站带来巨大的经济损失。因此，安全拉杆的工作寿命也是浮式拦污排结构设计需要考虑的关键问题。

由于各个水电站的枢纽布置、环境、水流等情况存在较大差异，目前拦污排尚没有形成统一的设计规程以适应不同水电站的实际需求。大部分拦污排参考现有工程及经验进行设计和分析[2-3]，欠缺拦污排工作强度等方面的研究，导致拦污排长时间在复杂环境下工作存在安全风险。徐远杰等[4-5]利用柔性多体系统动力学理论，建立了拦污排的空间多刚体模型，构建了拦污排的三维控制方程，进行数值解的迭代计算，通过该方法计算出特定情况下拦污排在空间中的平衡形状，并可求出拦污排上各点的张力，但其研究没有综合考虑漂浮物堆积对拦污排的影响。流固耦合方法是解决流体与固体相互作用工程问题的有效方法之一，应用于水力机械的优化研究取得了许多重要成果[6-9]，但该方法应用于拦污排设计研究几乎还没有涉及。

本文结合广西郁江某水电站浮式拦污排进行研究，该电站浮式拦污排情况如图1所示。在漂浮物和水流长期冲击的影响下，拦污排安全拉杆发生断裂，安全拉杆疲劳断裂情况如图2所示。断裂截面一侧出现疲劳条带，另一侧断口形貌粗糙，为瞬时断裂区，该特征为承受单向弯曲载荷下的疲劳断裂特征。研究采用流固耦合方法，根据实际情况建立拦污排有限元模型，基于单向流固耦合计算出安全拉杆断裂处应力值，更改拦污排浮箱数量以调整拦污排结构布局，比较安全拉杆断裂处应力值的变化情况，分析拦污排结构布局对安全拉杆应力值的影响，以实现调整浮箱数量达到拦污排结构优化的目的。

图1 电站浮式拦污排示意图

图2 安全拉杆疲劳断裂情况

1 流固耦合计算

1.1 计算方法

流固耦合问题是流体与固体的物理场之间相互作用问题，是流体、固体两相介质之间的相互作用[10]。

ANSYS中求解流固耦合问题的方式是分离求解，在流体求解器和结构求解器上计算各自的物理变量。按两求解器的数据传递方式，流固耦合可分为单向流固耦合和双向流固耦合。单向流固耦合只考虑流体对固体的影响，认为流体作用于固体造成的固体变形对流体影响较小，可以忽略不计；双向流固耦合对流场和结构迭代计算，考虑了耦合面变形的影响[11]。由于拦污排模型结构复杂、体积大，加之双向流固耦合方法本身会占用庞大的计算资源，使用该方法直接分析拦污排模型动态特性难以实现。本文采用单向流固耦合方法对拦污排的研究，主要考虑拦污排静态结构性能。拦污排的单向流固耦合实现过程[12]是：在Fluent模块下对流体域进行数值模拟，计算出流固耦合面上的水压力载荷，拦污排的流固耦合面为各个浮箱与漂浮物与水的接触面；然后直接将压力载荷加载到结构域耦合面上，在结构域中做静力学计算进行有限元应力分析，整个耦合计算过程在Static Structural模块中实现，两域的数据传递通过网格映射关系实现。

本文拦污排周围流体的计算湍流模型采用标准k-ε湍流模型，其控制方程为雷诺平均N-S方程，包括连续方程和动量方程[13-14]连续方程和动量方程如下：

(1)

(2)

本文基于单向流固耦合对拦污排模型进行稳态计算，其结构应力学线形分析方程[15]为

σ=BDK-1F，

(3)

式中，σ为应力矩阵；B为弹性矩阵；D为应变矢量；K为刚度矩阵；F为力矩阵。

等效应力按第四强度理论[16]计算：

(4)

式中，σ1、σ2、σ3为一个作用点的3个相互垂直的主应力；σe等效应力。

1.2 结构域计算模型

本文所研究的浮式拦污排共由32个浮箱组成，各浮箱之间使用连接拉杆连接；上下两支墩设置活动锚头，可随水位调节拦污排高度；浮箱与上支墩的活动锚头利用连接拉杆连接，浮箱与下支墩的活动锚头使用安全拉杆连接；下支墩位于河流中心，水流速度较大，上支墩建立在河岸上。受水流和漂浮物影响，拦污排工作时布置情况如图3所示。

图3 浮式拦污排布置简图

结构域计算模型包括拦污排和漂浮物有限元模型。拦污排为装配体，按图纸建立有限元模型，忽略对整体影响较小的细节，浮箱间的位置关系近似还原实际工作情况。漂浮物主要为树木和生活垃圾等，堆积在拦污挂栅前会造成拦污排受水流作用面积增大，安全拉杆承压增大。为便于研究，将每一个挂栅前漂浮物视作一个整体，并将其简化为一个长方体模型作用于挂栅。图4给出了结构域计算模型。结构域模型材料参数定义：拦污排模型材料为Q235钢；漂浮物主要为树木，这里规定漂浮物模型材料为木材，模型材料属性见表1。

图4 结构域计算模型

表1 模型材料属性

拦污排零件多、整体尺寸大且几何形状复杂，为保证结构域模型的网格质量，浮箱模型进行切割分块处理并组合成多体零件进行网格划分；浮箱模型网格如图5所示，安全拉杆模型网格如图6所示。

图5 浮箱模型网格

图6 安全拉杆模型网格

1.3 流体域计算模型

流体域是截取的拦污排所在河流段水域，所取流体域尺寸为长度216 m，宽度103 m，高度3 m。拦污排入水部分界面为流固耦合边界。通常结构域和流体域模型在边界面上的节点并不重合、网格不相同，有限元中采用插值法计算流体作用在结构上的应力，因此两域模式可以采用不同的网格划分方法[17]。由于耦合边界面存在许多狭长缝隙且分布不规律，流体域模型选择四面体网格划分方法，尺寸功能选择Proximity控制狭长缝隙的单元数量。流体域网格信息见表2。

表2 流体域网格信息

设置流体域进口边界条件为速度入口，通过UDF定义进口边界流速呈抛物线分布，最大流速 2 km/h，河岸水流速趋于0，近似模拟实际河流中非线性流速情况，进口流速分布情况如图7所示。出口边界条件设置为自由出口，壁面边界条件设置为滑移边界，两域流固耦合边界设置为无滑移边界。

图7 进口流速分布情况

1.4 计算结果分析

在实际情况下，拦污排所在河流段水流状况复杂多变，来流流速非定常，拦污排拦截的漂浮物呈无法估算地动态积累与减少。这种复杂的实际工作环境状况在ANSYS工作环境下难以对数值进行精确模拟，且复杂工况的数值模拟会带来极大计算量，因此，上述两域计算模型建立过程进行了必要的简化。下面结合拦污排实际工作情况与流固耦合计算结果对比，分析简化的两域模型与实际情况是否大致相符。流固耦合计算包括流体域瞬态数值计算与结构域静力学计算结果。图8为流体域瞬态数值计算得到的流体域速度流线图。从图8可知，在水流速度较大的流域，拦污排后方会出现回流现象，流速小的地方基本无回流出现。观察实际水流情况发现，水流速度较大的河流中段处拦污排后方区域有明显的回流现象，而接近河岸水流速度小的区域回流现象不明显；从图1能看出，河流中段处拦污排后方出现有漂浮物堆积现象，反映了流体回流情况，而接近河岸的拦污排后方无漂浮物堆积。流体域数值计算结果与实际情况基本相符合，说明文中建立的流体域计算模型用于拦污排流固耦合计算是可行的。

图8 流体域速度流线图

将在流体域中计算得到的流固耦合面的压力分布载荷导入静力学分析模块，图9为浮箱及漂浮物压力载荷分布情况(俯视图)。对结构域进行有限元应力分析，得到拦污排整体等效应力应变情况。安全拉杆连接着支墩和拦污排，作用是防止拦污排拉力过大损坏支墩，所以在安全拉杆中间设计小凹槽限制最大拉力。疲劳断裂通常发生在安全拉杆中间截面突变处，因此本文结构域静力学分析主要观察安全拉杆的应力和应变情况，以安全拉杆的应力值为指标判断结构域模型的正确性。计算结果显示，拦污排最大应力应变出现在安全拉杆上，图10给出了安全拉杆在耦合计算下的应力及应变情况。耦合计算得到的安全拉杆断裂处应力值为102.9 MPa，以工程中安全因数为2，该应力情况满足强度条件但存在着疲劳断裂隐患，与安全拉杆实际应力情况相近，该模型可用于后续拦污排结构的优化分析。

图9 浮箱及漂浮物的压力载荷分布情况

(a) 安全拉杆应力

2 拦污排结构优化及分析

2.1 优化方案设计

据水电站工作人员记录，安全拉杆1～2 a出现一次疲劳断裂。安全拉杆寿命短、频繁疲劳断裂，说明拦污排设计存在不合理之处，需要对结构进行优化。根据现场对拦污排的分析，拦污排整体尺寸大，在水流和漂浮物的综合影响下拦污排结构布局对安全拉杆受力情况会有重大影响。为了降低安全拉杆受力大小、提高工作寿命，本文从结构布局的角度着手，通过改变浮箱数量调整拦污排结构布局，研究不同浮箱数量情况的拦污排结构布局与安全拉杆应力值之间的关系，确定该拦污排模型中使安全拉杆应力值达到最小的浮箱数量布局方案。

目前水电站使用的拦污排浮箱数量为32，当浮箱数量为29时拦污排在两支墩之间近似呈直线分布，浮箱数量为n的拦污排位置如图11所示。建立浮箱数量分别为29、30、31、32及33的拦污排结构域模型，流体域模型按上述方法建立，采用单向流固耦合方法计算安全拉杆的应力。考虑拦污排前堆积的漂浮物数量是非稳定的，对不同漂浮物堆积情况进行分析。漂浮物作用于拦污挂栅实质上造成整个拦污排受水压力面积增大。将每一个浮箱前堆积的漂浮物视为一个整体，作用于拦污挂栅，增大流固耦合面。按占据拦污挂栅的面积比例量化估算漂浮物堆积，如图12给出了浮箱前堆积的漂浮物量化情况。计算在定流速下拦污挂栅无漂浮物堆积、堆积漂浮物占40%及堆满漂浮物三种情况的安全拉杆应力值，以安全拉杆应力值的变化情况为指标分析拦污排设计的优劣，并推出适用于实际情况的最合理浮箱数量结构布局。

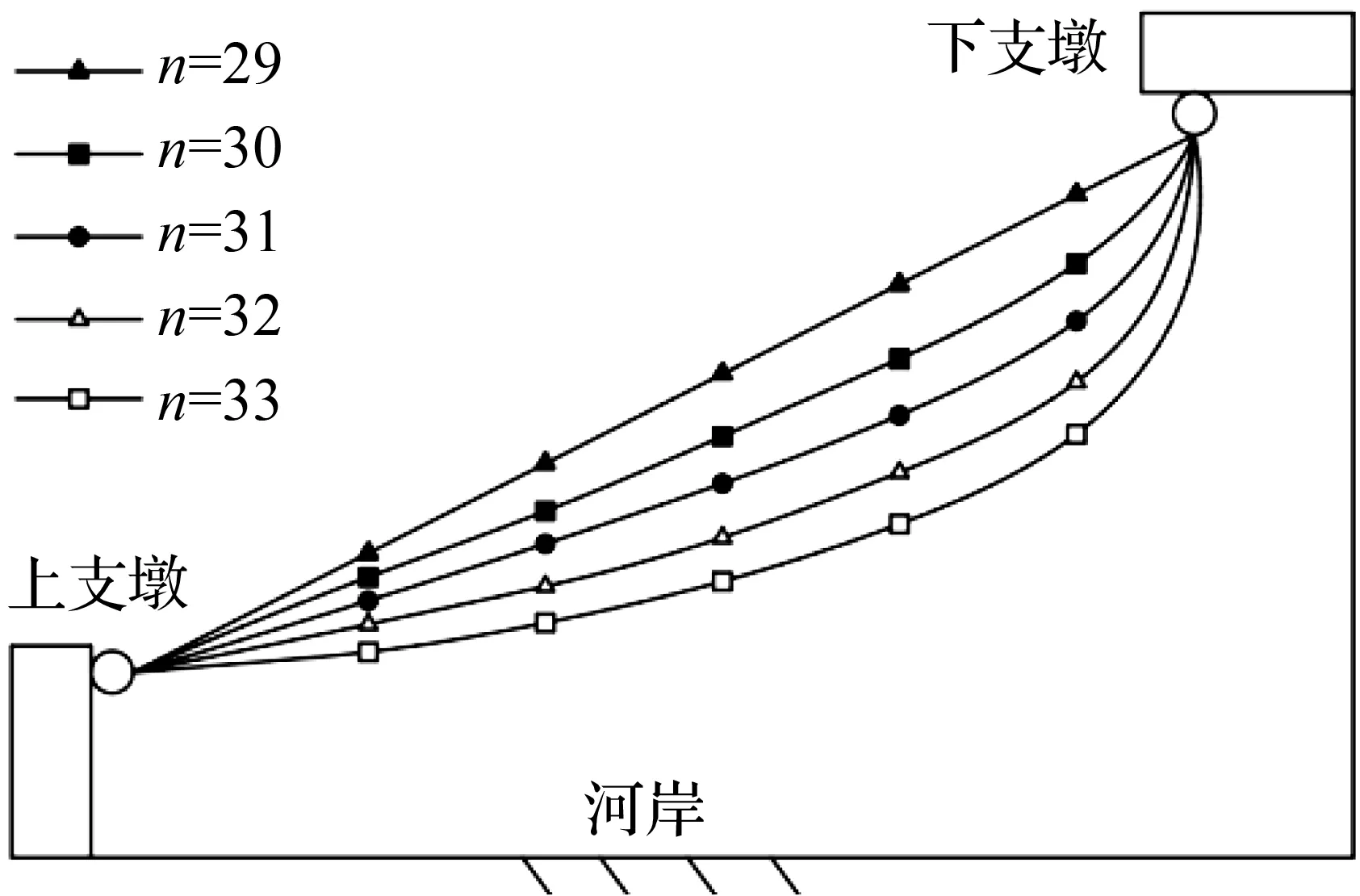
图11 浮箱数量为n的拦污排位置

(a) 浮箱前堆积漂浮物约占40 %

2.2 结果对比分析

假设拦污排所处河段中间最大流速的平均值为2 km/h，对不同漂浮物堆积情况下不同浮箱数量的拦污排模型进行计算分析。图13至图15列出了在无漂浮物、堆积漂浮物占40%及堆满漂浮物3种情况下浮箱数量分别为29、30、31、32及33的安全拉杆应力值。

(a) 浮箱数量为29所对应的安全拉杆应力

(a) 浮箱数量为29所对应的安全拉杆应力

(a) 浮箱数量为29所对应的安全拉杆应力

图16给出了三种漂浮物堆积情况下，不同浮箱数量拦污排模型的安全拉杆断裂处应力情况。从图16可看出，不同浮箱数量下的拦污排模型安全拉杆断裂处应力值有明显差异，且堆积的漂浮物越多，差异越明显；从无漂浮物到堆满漂浮物的过程中，随浮箱数量的增加，安全拉杆的应力变化范围和平均应力值均呈现先增大后减小的变化趋势，可见基于改变浮箱数量的拦污排结构优化是合理有效的。针对本文模型，采用30个浮箱组成的拦污排结构更为合适，能降低漂浮物堆积过程中安全拉杆平均应力值、减小应力幅，进而提高安全拉杆工作寿命。

图16 三种漂浮物堆积情况下不同浮箱数量对应的安全拉杆应力值变化

3 结论

本文建立某水电站拦污排在额定流速条件下的流固耦合计算模型，将计算结果与现场实际情况对比，证明了模型的正确性。针对安全拉杆工作寿命短、频繁疲劳断裂的问题，从改变浮箱数量来调整拦污排结构布局的角度进行优化。为了研究实际工况下合理的拦污排结构布局，建立3种漂浮物堆积情况下浮箱数量从29到33的拦污排耦合计算模型，比较基于单向流固耦合方法计算得到的各模型中安全拉杆断裂处应力值，得出以下结论：

① 调整浮箱数量以改变拦污排结构布局会对安全拉杆应力有明显影响；

② 在拦污排长度足够的前提下，增加浮箱数量改变拦污排布局，漂浮物堆积过程中安全拉杆平均应力值与应力幅呈现减小后增大的变化趋势，选择合适的浮箱数量、设计合理的拦污排结构布局是提高拦污排工作寿命的有效方式。