初始温度取值方法对混凝土箱梁温度场的影响

薛俊青，李哲熙，林健辉，布里斯杰拉·布鲁诺，黄福云

(福州大学 土木工程学院， 福建 福州 350108)

0 引言

温度应力是导致混凝土箱梁出现开裂的主要原因之一[1-5]。主梁纵向温度场通常可假定均匀[1]，而主梁截面温度场主要受到材料热工参数、横截面几何形状和尺寸、地理因素和气象条件的影响，影响因素众多且复杂，较难依靠经典的传导方程进行精确计算[6-8]。有限元法是求解主梁截面温度场时最常用且最有效的方法之一。采用有限元法进行主梁截面温度场模拟时，边界条件的准确性对计算结果的精确性影响较大，通常采用输入综合环境温度和综合换热系数的方法模拟边界条件[3-4,6,9-14]。对于边界条件必须给定一个初始稳态条件，需要确定有限元模型中所有节点在初始时刻的温度值，即整个截面的初始温度场。

学者们通常采用连续计算多天(包括目标日期及之前多天)的方法减小初始温度取值误差[1, 4,6, 9-12]。对比国内外学者采用的初始温度取值方法可以发现主要分为以下两类：将初始温度与环境温度建立联系[15-17]和将初始温度与桥梁截面平均温度建立联系[3, 6,9-11, 13]。KIM等[15]采用日出前的环境温度作为初始温度(以下简称为：日出环温法)；王毅[16]选取日出前后的环境温度作为初始温度初值进行计算，将第一次计算结束时的截面温度场作为第二次的初始温度场并重复施加第一次的边界条件，以此循环，直到前后两次计算结束时的截面温度场之间误差小于限值，将该次计算结束时的截面温度场作为模型计算的初始温度(以下简称为：迭代计算法)；LEE等[17]采用零点时刻的环境温度作为初始温度(以下简称为：零点环温法)。部分学者采用零点时刻桥梁截面平均温度实测值作为初始温度，其中TAYI等[3]采用目标日期之前多天的环境温度、风速和太阳辐射实测数据作为边界条件进行多天计算(以下简称为：零点均温法)；还有学者针对零点均温法进行简化，选择目标日期当天的实测环境温度、风速和太阳辐射数据作为边界条件循环计算多天[6, 9-11, 13](以下简称为：零点均温循环法)。对比不同初始温度取值方法发现，将初始温度与环境温度建立联系的方法无需花费人力物力进行现场采集且适合大范围使用。但是其中日出环温法需查询日出时间，迭代计算法需要进行多次误差对比，均较为繁琐。将初始温度与桥梁截面平均温度建立联系的方法(零点环温法和零点均温循环法)需要在现场埋置温度传感器并进行温度数据采集，不适合大范围使用。采用各种初始温度取值方法建立的有限元模型能否精确模拟箱梁截面温度场均有待考证。

为此，本文以深圳市某座混凝土箱梁桥为背景工程，实测该桥箱梁截面温度场，与采用不同初始温度取值方法建立的箱梁截面有限元模型计算结果对比，分析不同初始温度取值方法对混凝土箱梁截面温度场的影响，并给出初始温度的建议取值方法。

1 工程背景

以深圳市某座混凝土箱梁桥为背景工程。该桥主梁采用C50混凝土，单跨长度为30 m，横截面为单箱三室，顶板宽度17.0 m，底板宽度11.3 m，高度为1.6 m，纵断面和横截面尺寸如图1所示[6]。主梁横截面共布设18个温度传感器，其中顶板5个(T-1～T-5)；底板3个(B-1～B-3)；左右腹板沿腹板从顶板中心线到底板中心线各4个(W-1～4和W-7～10)和中腹板2个(W-5和W-6)，具体布置如图1(b)所示。由于篇幅限制，仅选取夏季温度实测时段(2017年8月10日～13日)的数据进行分析。

(a) 纵断面

(b) 横截面

箱梁温度场测试仪器如图2所示，主梁采用现场浇筑施工，在绑扎主梁钢筋时，安装温度传感器，如图2(a)所示。将温度传感器数据线从底板排水孔伸出，汇集为一束，沿着梁底引至桥台处采集箱，如图2(b)所示。使用四川金码公司生产的自动化综合采集系统每隔0.5 h采集一次温度传感器数据，如图2(c)所示。同时使用小型移动式气象站每隔0.5 h采集一次桥址处的环境温度、太阳辐射、风速等气象数据，如图2(d)所示。

(a) 主梁温度传感器安装

2 有限元模拟

采用有限元软件MIDAS-FEA中适合二维稳态及瞬态分析的2D平面应变单元，并根据图1(b)截面尺寸建立的箱梁截面有限元模型如图3所示。混凝土密度、导热系数和比热容分别取2 500 kg/m3、1.5 W/(m·℃)和900 J/(kg·℃)[6]。箱梁外边界条件的综合环境温度为箱外太阳辐射、对流换热和辐射换热作用叠加在环境温度上得到的等效温度；综合换热系数为对流换热系数和辐射换热系数的叠加。顶板上表面受到太阳直射和太阳散射作用；腹板外表面非阴影区受到太阳直射、太阳散射和地面反射作用，腹板外表面阴影区受到太阳散射和地面反射作用；底板下缘和翼缘板下缘仅受到地面反射作用[6]。箱梁内边界条件采用实测箱内温度日变化曲线作为综合环境温度，对流换热系数为综合换热系数[9]。有限元模型网格划分尺寸为0.02 m，共划分为37 017个单元，35 659个节点，箱梁截面有限元模型如图3所示。每个节点设置一个温度自由度，每0.5 h为一个时间分析步。为验证MIDAS-FEA建立的有限元模型精确性，采用ANSYS有限元软件，选用平面四边形单元plane55建立有限元模型。对比结果显示，MIDAS-FEA建立的有限元模型精确性满足要求[9]。

图3 箱梁截面有限元模型

分别采用引言总结的多种初始温度取值方法及多天的有限元边界条件建立有限元模型，包括：①日出环温法(取2017年8月10日6点的环境温度27 ℃作为初始温度，4 d的有限元边界条件为2017年8月10日～13日实测环境温度、风速和太阳辐射数据(以下简称：实测边界条件))；②零点环温法(取2017年8月10日0点的环境温度27.7 ℃作为初始温度，4 d的有限元边界条件为实测边界条件)；③零点均温法(取2017年8月10日0点的实测截面平均温度32.8 ℃作为初始温度，4 d的有限元边界条件为实测边界条件)；④零点均温循环法(取2017年8月13日0点的实测截面平均温度34.2 ℃作为初始温度，4 d的有限元边界条件均为2017年8月13日实测环境温度、风速和太阳辐射数据(以下简称：循环边界条件))。本文对零点环温法进行简化，选择目标日期当天的实测环境温度、风速和太阳辐射数据作为边界条件循环计算多天(以下简称为：零点环温循环法，即取2017年8月13日0点的环境温度27.7 ℃作为初始温度，4 d的有限元边界条件为循环边界条件)。为对比采用连续计算多天的方法有效性，建立仅计算目标日期温度的有限元模型(取2017年8月13日6点的环境温度27 ℃作为初始温度，单日的有限元边界条件为2017年8月13日实测环境温度、风速和太阳辐射数据进行计算，以下简称：单日日出环温法)。迭代计算法由于使用繁琐，且无明显优点，因此本文不进行讨论。

3 不同初始温度取值方法对箱梁截面温度场影响

3.1 对箱梁截面温度日变化曲线影响

由于篇幅限制，仅选取箱梁截面左侧测点(T-2、W-1、W-3和B-1测点)，开展采用不同初始温度取值方法的有限元计算温度日变化曲线与实测结果比较分析，温度日变化曲线实测值与不同初始温度取值方法的有限元计算对比如图4所示。采用均方根误差(ERMS)和平均相对误差(EMAP)定量考察有限元计算曲线和实测曲线的拟合程度[9]，不同温度测点ERMS和EMAP对比见表1。

从图4可以看出，采用单日日出环温法的有限元模型计算温度曲线与实测曲线误差远大于其他初始温度取值方法，ERMS达到2.46～5.74 ℃，EMAP达到7.29%～16.35%。可以判断采用连续计算多天的方法减小初始温度取值误差是必要的。在第4天(8月13日)时，采用不同初始温度取值方法并连续计算四天的有限元模型计算温度曲线与实测曲线误差均较小。图4(a)和图4(d)可以看出，对于顶板T-2测点和底板B-1测点，采用零点环温循环法和零点均温循环法的有限元模型计算温度曲线与实测曲线误差最小(ERMS小于0.39 ℃，EMAP小于0.94%，见表1)。从图4(b)和表1可以看出，对于腹板W-1测点，采用日出环温法、零点环温法和零点环温循环法的有限元模型计算温度曲线与实测曲线误差最小(ERMS小于0.45 ℃，EMAP小于1.27%)。从图4(c)和表1可以看出，对于腹板W-3测点，采用零点环温循环法和零点均温法的有限元模型计算温度曲线与实测曲线误差最小(ERMS小于0.13 ℃，EMAP小于0.36%)。采用零点环温循环法的有限元模型各测点的计算温度曲线与实测曲线均吻合较好；目标日期零点的环境温度可通过气象网站查询获得，无需花费人力物力进行现场截面温度采集；循环采用目标日期的实测环境温度、风速和太阳辐射数据作为有限元边界条件可有效减少实测边界条件的工作量。可以总结发现，采用零点环温循环法作为初始温度取值方法可高精度高效率地建立有限元模型分析箱梁截面温度日变化曲线，且适合大范围使用。

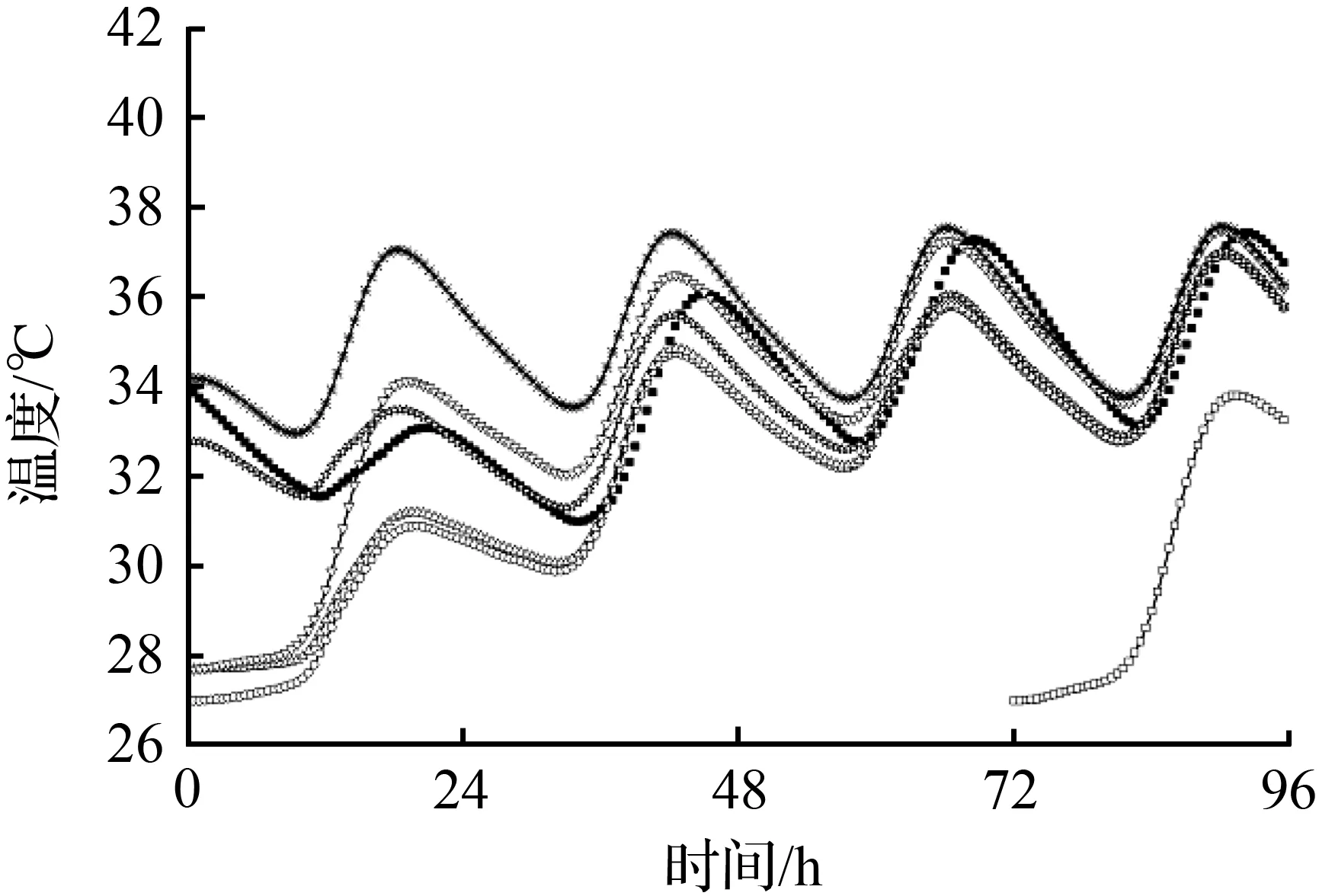
(a) T-2测点

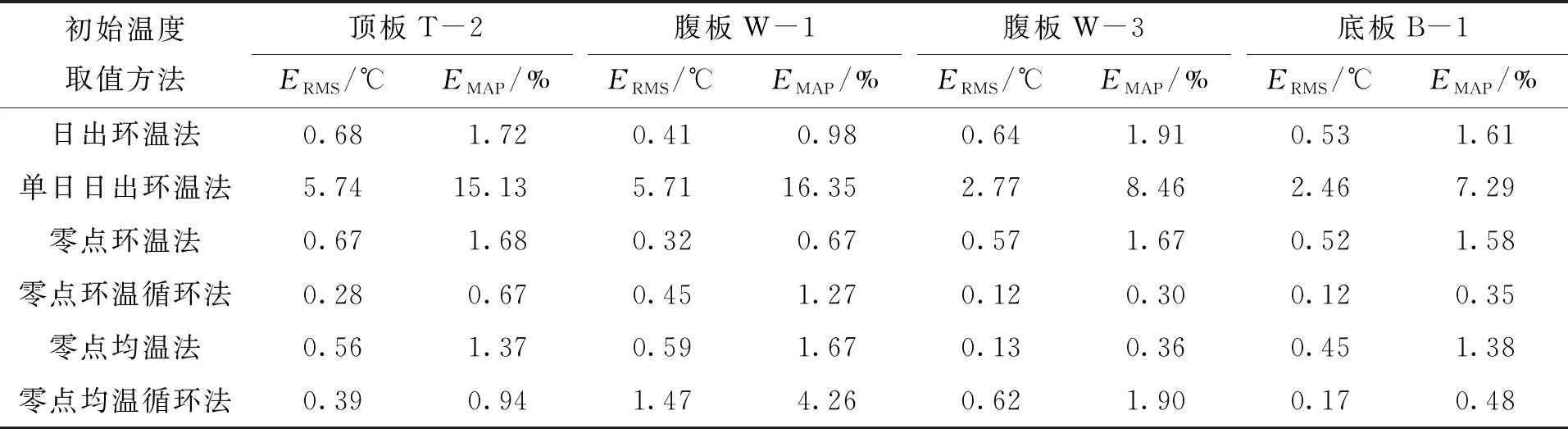
表1 不同温度测点ERMS和EMAP对比

3.2 对箱梁截面平均温度峰值影响

截面平均温度峰值对应桥梁结构顺桥向胀缩变形峰值。将主梁截面上所有单元的温度与对应单元面积的乘积进行加总后再除以所有单元总面积，就可以求得主梁截面平均温度[10]。不同初始温度取值方法的有限元计算截面平均温度最高值与实测值对比见表2，与8月13日的实测主梁截面平均温度最高值对比发现，采用单日日出环温法的有限元计算截面平均温度最高值的差值较大，达到3.3 ℃。因此采用单日日出环温法计算截面平均温度峰值误差较大，不建议采用。而采用不同初始温度取值方法并连续计算四天的有限元计算截面平均温度最高值与实测值误差均较小。其中，采用零点环温循环法的有限元计算截面平均温度最高值与实测值一致。

表2 不同初始温度取值方法的有限元计算截面平均温度最高值与实测值对比

3.3 对箱梁截面温度梯度影响

对于超静定体系的桥梁结构，混凝土箱梁截面竖向温差和横向温差会产生温度次应力和自应力[1]。从前面分析可以得到采用单日日出环温法作为初始温度取值方法计算误差较大，因此本次不考虑单日日出环温法。不同初始温度取值方法的箱梁截面温差有限元计算曲线对比如图5所示，图5(a)中竖坐标为距顶板上缘的距离，0～22 cm属于顶板，22～132 cm属于腹板，132～160 cm属于底板。通过对比分析可以发现，不同初始温度取值方法对于箱梁截面竖向温度梯度计算曲线整体变化趋势影响较小，对腹板区域有一定影响(最大差值约0.9 ℃)。对于最不利的箱梁顶板表面正温差峰值，采用零点环温循环法和日出环温法的有限元计算值最高(16.5 ℃)，结果偏安全，满足工程需要。由图5(b)可以看出，不同初始温度取值方法对于箱梁截面顶板横向温度梯度计算曲线有一定影响(最大差值约2.0 ℃)。其中，采用零点环温循环法的顶板横向温度梯度计算曲线与实测值误差最小，且结果偏安全，满足工程需要。

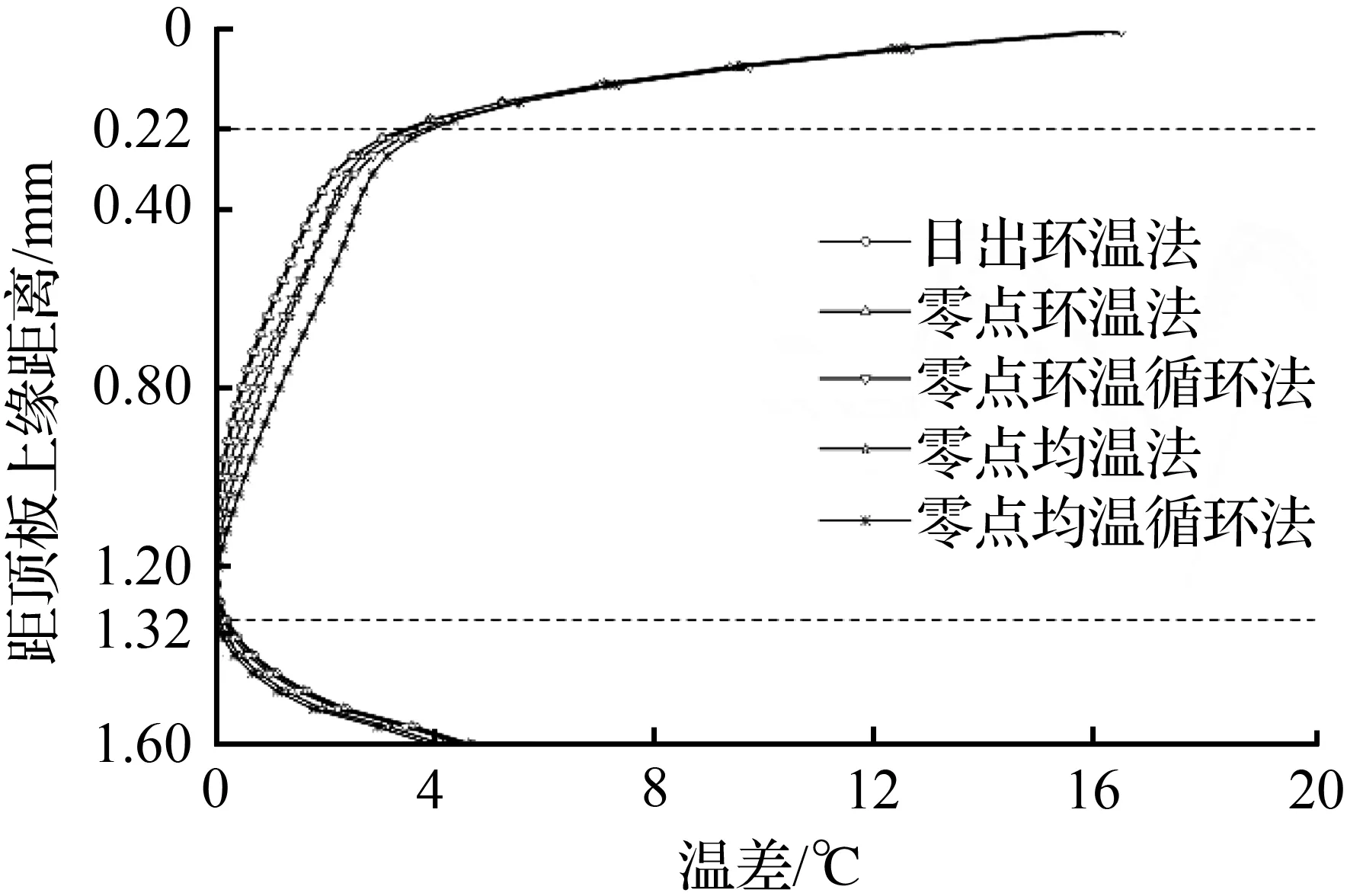
(a) 最大竖向正温差

4 结语

本文通过温度实测、有限元模拟和参数分析，主要得到以下结论：

① 采用单日日出环温法的有限元模型计算温度曲线和截面平均温度最高值与实测值误差远大于其他初始温度取值方法，可以判断采用连续计算多天的方法减小初始温度取值误差是必要的。

② 采用不同初始温度取值方法并连续计算四天的有限元模型计算温度曲线和截面平均温度最高值与实测值误差均较小。采用不同初始温度取值方法对于箱梁截面竖向温度梯度计算曲线整体变化趋势影响较小，对腹板区域有一定影响。

③ 采用零点环温循环法的有限元模型各测点的计算温度曲线，截面平均温度最高值和顶板横向温度梯度计算曲线均与实测值吻合较好；最不利的箱梁顶板表面正温差峰值最高，结果偏安全，满足工程需要。

④ 考虑到零点环温循环法所采用的目标日期零点的环境温度可通过气象网站查询获得，无需花费人力物力进行现场截面温度采集，适合大范围使用；循环采用目标日期的实测环境温度、风速和太阳辐射数据作为有限元边界条件可有效减少实测边界条件的工作量。建议采用零点环温循环法作为初始温度取值方法可高精度高效率地建立有限元模型分析箱梁截面温度场。