基于结构熵的注意力流网络异构性研究

马满福，郭晨彪，李 勇，张钟颖，张 强，王常青

1.西北师范大学 计算机科学与工程学院，兰州 730070

2.中国互联网络信息中心 互联网基础技术开放实验室，北京 100190

复杂网络能够很好地描述自然科学、社会科学、管理科学和工程技术领域等相互关联的复杂模型，是研究复杂系统中子系统交互和关系的重要工具，是网络科学中重要的研究方法[1]。钱学森给出了复杂网络的一个较严格的定义：具有自组织、自相似、吸引子、小世界、无标度中部分或全部性质的网络称为复杂网络。复杂网络结构复杂且节点数目巨大，呈现多种不同特征，虽然各部分之间相互联系，但在功能结构上存在差异[2-3]。网络的拓扑性质、功能以及动力学行为均与网络的复杂性紧密相连，复杂网络中节点间的联系对于网络复杂性刻画十分有意义，也一直是复杂网络研究的热点[4]。

复杂系统中病毒传播[5]、社区结构划分[6]、节点重要性排序分析[7-9]、信息扩散[10]等，都与网络的异构性不无关系[11-12]。熵是描述复杂系统结构的物理量，而关系结构的熵可以定量描述网络状态，是测度网络结构无序性的重要指标。通过定义网络结构熵评价网络异构性，一般地，网络结构熵值越小，网络越混乱，意味着网络各部分间的差异越大，异构性越强；反之网络结构熵越大，网络越有序，意味着网络结构越趋于均衡，异构性越弱[13-15]。目前，已有大量的研究各自从不同角度出发提出定义网络结构熵，主要有度分布熵[15]、吴结构熵[16]、剩余度熵[15]、蔡结构熵[17-19]等。

网络结构熵是研究复杂网络的重要工具，能够很好地度量网络结构的特征，反映了网络节点和链路的异构性。传统的异构性度量指标度分布熵、吴结构熵、SD结构熵等，均从网络中“点”或“边”的特征来定义结构熵。注意力流网络是基于在线行为数据，通过点击网站序列而构建成的有向加权图。在网络中的节点代表Web站点，用户从一个Web站点通过点击跳转到了另一个Web站点形成边，站点之间的跳转次数表示边的权值，Web站点的特殊属性就是站点的停留时长。根据注意力流网络的结构特征，传统的网络结构熵不能准确地度量注意力流网络的异构性。因此，寻找一种针对注意力流网络异构性特征的测度方法是本文研究的目的所在。本文的主要贡献如下：

（1）以中国互联网信息中心（CNNIC）提供的海量在线上网行为大数据构建注意力流网络。

（2）基于复杂网络结构异构性的研究方法，结合注意力流网络的站点及结构特征，建立了注意力流网络拓扑结构站点重要度的评价指标，构建了注意力流网络结构熵模型，提出了注意力流网络异构性度量算法ANSE。

（3）通过实验分析，注意力流网络结构熵够更好地刻画注意力流网络的结构特征，准确地度量注意力流网络中各站点的差异性，从而分析各网络各站点的属性特征。

1 相关工作

1.1 注意力流网络

注意力流网络作为网络科学的一个重要分支，吸引了大量的研究人员的关注。基于加权复杂网络方法研究注意力流网络，研究人员在已有的研究中发现了多个重要的普适规律，例如：Web站点间注意力流演化的异速标度律和耗散律、在注意力流网络中发现了引力律、在注意力流中还发现了Heaps律等[20-23]。文献[24]提出了一种在不同网站之间分配和流动的几何表示方法，根据网站流动距离将大量网站嵌入20维欧氏空间中，发现20%受欢迎的网站吸引了75%的注意力流；文献[23]基于在线集体注意力流研究网站的站点影响力，将网络视为虚拟生物，根据代谢理论，网站必须吸收“能量”来生长、繁衍和发展，将新陈代谢和用户注意力的影响视为网站的能量，基于网络科学理论建立注意力流网络，研究了集体注意力在不同站点间的分布、流动以及Web的新陈代谢规律。研究发现站点的影响力与注意力在该站点上的停留时间呈亚线性关系，亦即Web版的Kleiber律。然而很少有学者研究注意力流网络异构性，研究注意力流网络的异构性，分析站点的差异及网络结构特征具有重要的理论意义和应用价值。

1.2 网络结构熵

网络结构熵主要基于网络中节点、边的特征来定义，其中网络节点的差异性由节点概率分布来度量。反映网络连接特征的熵有度分布熵、吴网络结构熵、蔡网络结构熵等。

（1）度分布熵[15]，以边为研究对象，根据网络节点度概率分布，对网络的异构性进行了测度，定义度分布网络结构熵。

（2）吴结构熵[16]，以节点为主体，通过分析网络节点所拥有的边的条数，即各节点度值之间的差异来反映网络的异构性，从而提出了基于网络中节点的特征的网络结构熵。

（3）SD结构熵[17]，为了综合考虑网络结构中“点”或者“边”的作用，蔡萌等综合考虑了“点”和“边”差异性，定义网络中节点的结构重要性，提出了一种新的SD网络结构熵，反映网络的异构性。

文献[15]指出度分布熵可以测度网络异构性，当网络中各节点的度值均不相同，即P(k)=1/(N-1)(∀k=1,2,…,N-1)时，网络的度分布熵取最大值，=ln(N-1)；相反，对于网络中各节点的度均相同的规则网络，则有，对于星型网络等特殊网络异构性度量的准确性不够。文献[16]吴结构熵以节点为主体，通过分析网络节点所拥有的边的条数，即各节点度值之间的差异来反映网络的异构性，吴结构熵的最小值对应于星型网络；最大值对应于最近邻耦合网络Hmaxwu=lnN，吴结构熵关注网络连接的度分布定义节点重要性，忽略了节点本身的特性，例如在稀疏网络中忽略了孤立节点对网络的影响。文献[17]从“点”差异性和“边”差异性两方面提出了点边差异性SD结构熵。该网络结构熵是一种有效度量网络异构性的指标，并对稀疏网络和星型网络有很好的解释，但该方法的本质仍是以节点度值为基础，与度分布熵和吴结构熵等其他指标一样，过多强调网络的局部特征，而忽略了特殊网络的拓扑特征。然而很少有学者研究注意力流网络异构性。

以上几种结构熵，均基于网络中节点、边的特征来定义的网络结构熵，针对注意力流网络的web站点停留时长等特殊属性不适用，即通过传统网络结构熵无法准确地度量注意力流网络Web站点的差异，对刻画注意力流网络异构性不够准确。因此，本文基于注意力流网络结构及Web站点的特征，定义注意力流网络结构熵，提出注意力流网络异构性算法。本文提出的注意力流网络异构性算法具有重要的理论意义与应用价值。从理论价值来看，异构性研究能够很好地刻画注意力流网络的结构特征，在站点重要性排序分析、网站影响力分析、网站分类、社区发现等研究中发挥重要作用；从应用价值来看，站点重要性排序等方面研究已广泛应用于网络舆情监控、个性化推荐、广告精准投放等方面。

2 注意力流网络结构熵

2.1 注意力流网络构建

在线用户行为日志数据采集中，用户每次一开机就会建立一个在线行为日志数据文件，该日志数据记录每两秒检查一次用户计算机当前的焦点窗口，如果检查相比前两秒发生了变化，则增加一条记录来描述当前焦点窗口信息。在保证用户隐私的前提下，详细记录了开机时间与上次关机时间、焦点窗口的窗口进程名称、URL地址、当前标签页句柄、程序名称、程序所属公司名称以及用户人口属性等信息。表1为在线点击流序列样例。

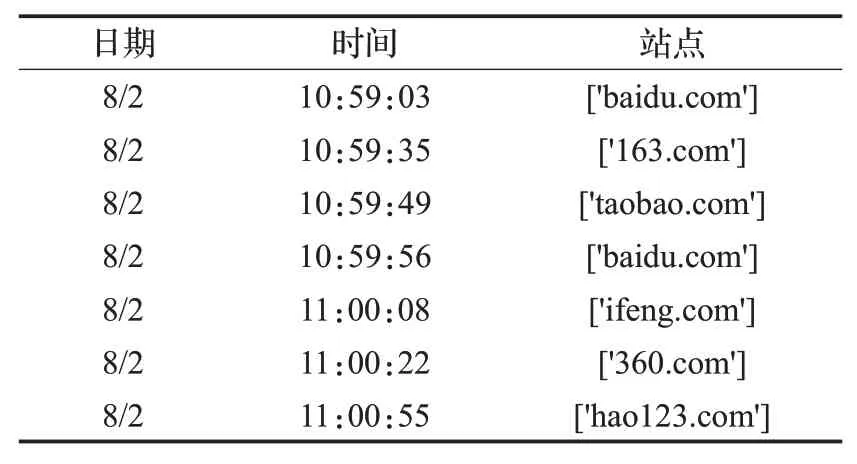
表1 在线点击流序列样例Table 1 Example of online clickstream sequence

对于一个有N个节点注意力流网络，其拓扑结构由一个加权有向图G=(V,E,T,Z)表示，如图1所示。其中V={v0,v1,…, }vN+1表示N+2个注意力流网络的站点；E∈V×V为图中的边集；T表示集体用户在一个站点上停留的总时间；Z表示边E的权重，是一个正的自然数集，边权值Z表示各个站点间转换的强度，若不存在的边其权值为0，表示用户在网络中Web节点的入度或出度，注意力流网络示意图如图1所示。

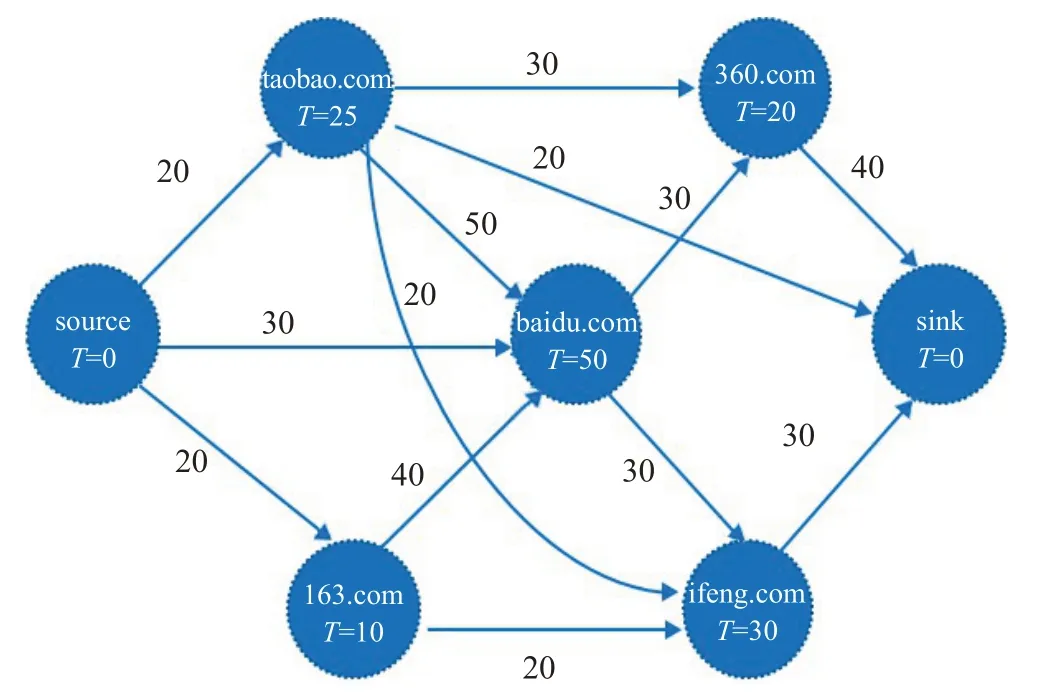
图1 注意力流网络示例Fig.1 Example of attention flow network

在一个会话期间（session），一个用户进入一个Web站点后必定会在一段时间后离开该Web站点，所以注意力流网络是平衡的，表明每个顶点的总入流（inflow）与总出流（outflow）相等关系。在网络中增加了两个额外节点“source”节点（表示为节点0）和“sink”节点（表示为节点N+1），分别表示点击流的“源”和“汇”。每个用户从“source”节点开始上网，当该会话结束后进入“sink”节点，用户结束其上网行为。会话（session）表示用户在一个Web站点上浏览的时间间隔，把会话时间间隔阈值定义为30分钟是学术界针对万维网研究普遍采用的标准值[25]。

2.2 注意力流网络结构熵模型

根据传统的网络结构熵模型，依据网络的结构特征，通过站点之间跳转的次数（即边的权值）、停留时间等，综合定义Web站点的流强度、站点之间的转移概率、站点总时长、站点吸引注意力的能力，结合Web站点的注意力总流量计算站点的综合力，用站点综合力来度量站点的差异性，刻画注意力流网络的异构性，基于此基础的Web站点重要度来定义注意力流网络结构熵。对比传统网络结构熵，该模型综合考虑了Web站点、站点之间的跳转、停留时间等，进而全面准确地度量注意力流网络的异构性。

通过网络有向图计算流矩阵，然后确定概率转移矩阵，由站点总时长计算对站点的吸引能力，最后通过站点耗散能力和概率转移矩阵得到基本矩阵。由基本矩阵计算从源节点到目的站点的总流量，最终得到网络站点的综合力。

在一个有N节点的注意力流网络中，网络中增加了两个额外节点“source”节点和“sink”节点，图G中定义一个带权(N+2)×(N+2)的流矩阵S(G)，流矩阵S(G)中的元素Zij=(i,j)表示从站点i到站点j的注意力流强度，Zij=0表示从站点i到站点j的无链路。图G的流矩阵S(G)可以表示为：

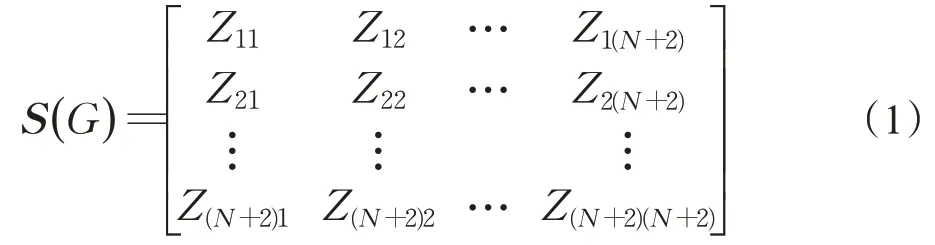
由流矩阵S(G)定义一个概率转移矩阵P(G)，P(G)表示图G上的马尔可夫链概率转移矩阵，其中，在概率转移矩阵P(G)中，Pij表示从站点i到站点j之间的转移概率。图G上的概率转移矩阵P(G)表示为：

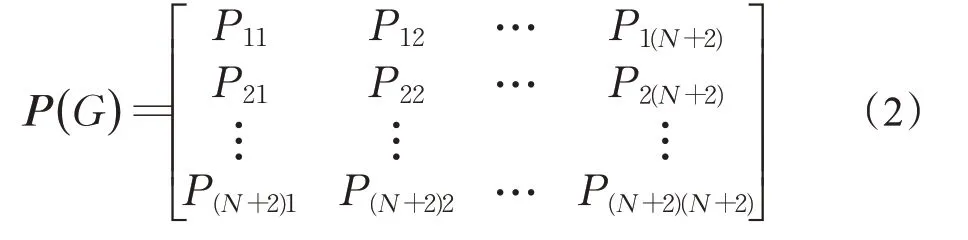
在注意力流网络中，假设有k个用户浏览了Web站点i，每个用户浏览的时间长度为tj，那么网络中所有用户在该Web节点的总时长Ti，定义总时长Ti为：

用βi表示Web站点i对注意力流的耗散能力，来度量Web站点吸引注意力的能力，采用文献[26]方法定义βi为：

定义矩阵D(G)为：Dij=βPij，由于β∈(0,]1，所以矩阵D(G)为去除源节点为(N+1)×(N+1)的矩阵。对于一个吸收马尔可夫链[27]，定义基本矩阵X(G)为：

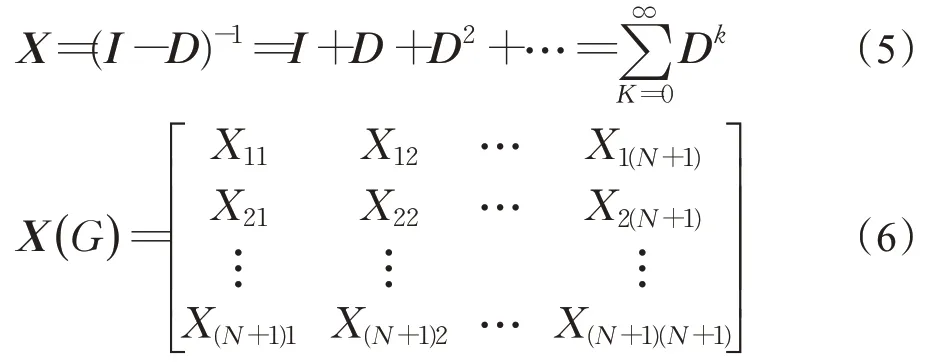
其中，I为单位矩阵。

由定义的基本矩阵计算源节点流到Web站点i的注意力总流量，用Mi来表示，Mi定义为：

根据Web站点i的注意力总流量来定义Web站点的综合力为：

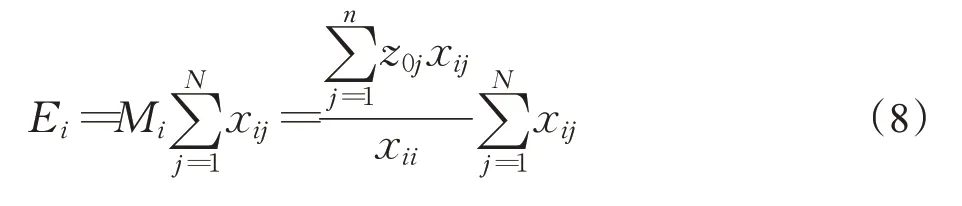
其中，Ei为Web站点i综合力，xij为基本矩阵X(G)中的元素。

通过Web站点的综合力的差异性来反映注意力流网络的异构性，提出基于注意力流网络站点特征的网络结构熵。

根据网络异构性矩阵、Web站点流强度、站点总时长、站点吸引注意力的能力等，结合Web站点的注意力总流量计算Web站点的综合力，可求得Web站点i相对重要度Ii，其计算公式为：

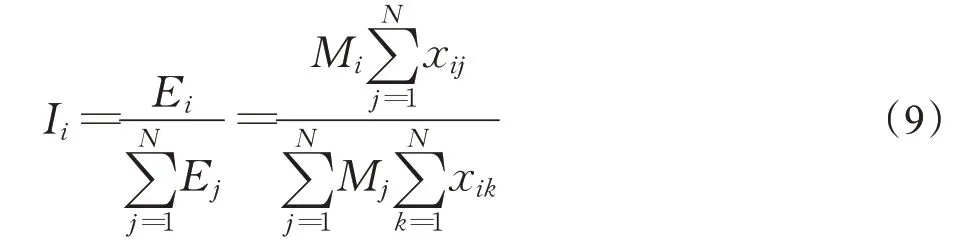
若某Web站点的综合力越大，可认为该站点在注意力流网络中的影响力越大，其Web站点越重要，为了衡量注意力流网络在各Web站点重要度或者影响力的差异，结合信息论中熵的计算方法，以及基于公式（9）Web站点i的重要度计算方法，可得到注意力流网络结构熵，其计算公式为：

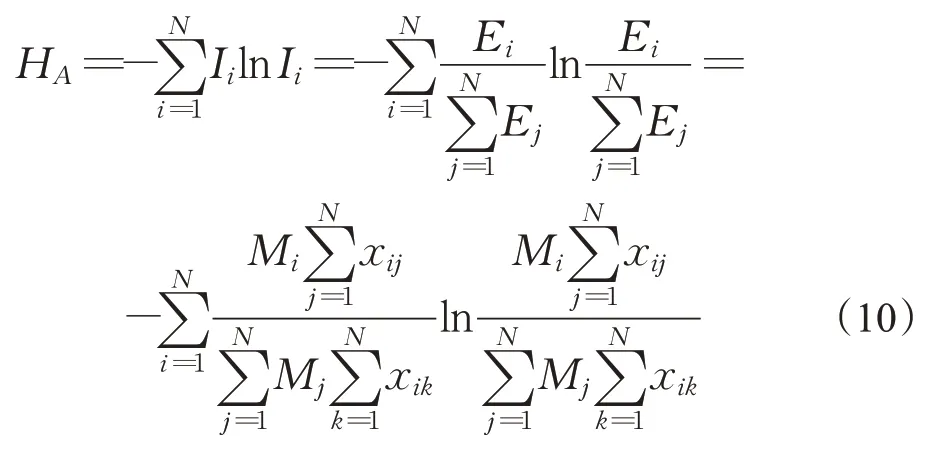
其中，HA为注意力流网络结构熵，Ii为站点的相对重要度。在注意力流网络中HA的值越小，说明网络在Web站点综合力尺度下的异构性越强，反之网络的异构则越弱。

2.3 注意力流网络结构熵算法ANSE

基于注意力流结构熵模型，提出注意力流网络结构熵算法ANSE（Attention flow Network Structural Entropy），由此得到网络的流矩阵、站点上停留时长、站点的综合力等，最终通过算法输出注意力流网络的结构熵。

算法1构建注意力流网络计算流矩阵

输入：Si={T,P,IDi}，其中T为开始时间，P表示为web站点，IDi表示用户标识；得到注意力流网络G=(V,E,T,Z)，V表示顶点集，E表示图中的边集，T表示顶点权重，Z表示流强度

输出：注意力流网络的流矩阵S(G)

1.G=nx.DiGraph

2.G.add_node（‘source’，time=0 pages=0）

3.G.add_node（‘sink’，time=0 pages=0）

4.For i in Si:

5. G.add_node（i，time）

算法2注意力流网络的基本矩阵算法

输入：注意力流网络的马尔可夫矩阵，网络Web站点总时长。

输出：基本矩阵X(G)

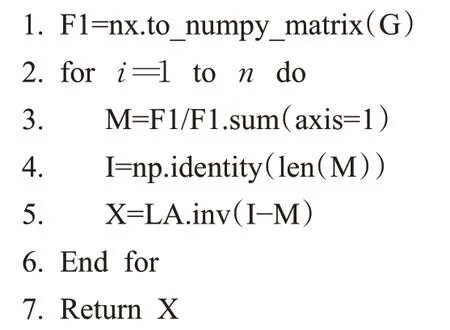
算法3注意力流网络结构熵算法

输入：注意力流网络基本矩阵X(G)及流矩阵S(G)

输出：注意力流网络结构熵值

3 实验分析

3.1 实验数据

以中国互联网信息中心（CNNIC）提供的海量在线用户行数据为实验数据，累积已达PB量级，该数据集为CNNIC目前提供的最新数据，为实验分析方便，本文随机抽取该数据集中1 000名用户1个月大约1.3亿条数据记录进行实验研究，数据样例如图2所示。

图2 在线行为日志数据样例Fig.2 Example of online behavior log data

3.2 注意力流网络结构特征分析

对在线行为日志数据进行清洗处理，使用网络科学的建模方法，Web站点看作节点，用户的站点转移流动看作边，站点停留时长作为节点权重，建立有向加权的注意力流网络，通过集体用户的数据构建集体注意力流网络图，构建的注意力流网络中拥有20 746个节点和135 771条边。注意力流网络图如图3所示。

图3 集体注意力流网络Fig.3 Collective attention flow network

在构造的注意力流网络中，分析注意力流网络出入度、站点的总停留时长的排名以及相关网络结构的其他特征。如图4是出度前20名的站点降序排名图，然后以出度为排序的方式绘制入度的折线图，从图上可以看出，其网络的站点出、入度值非常接近，而且每个站点出度和入度的排序基本是一致的，再次说明注意力流网络是平衡的。

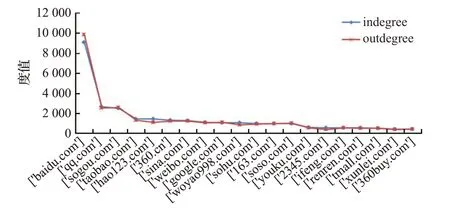
图4 站点度值前20降序排序图Fig.4 Descending order of top 20 websites

表2是所有站点总时间排名前10的站点，根据站点分析，排名前10的站点均为常用的站点，其中排名第一的qq.com为娱乐、社交、新闻类站点，第二的baidu.com为搜索引擎类网站，第三的taobao.com为购物类网站；对比停留时间排名与站点以度值排名的结果有差异，单独从站点度值或者总停留时长等方面排名来衡量站点的重要度是不准确的。因此需要从站点的度值、停留时长等多个方面综合度量站点差异性，以站点的综合力来测度网络结构的异构性。

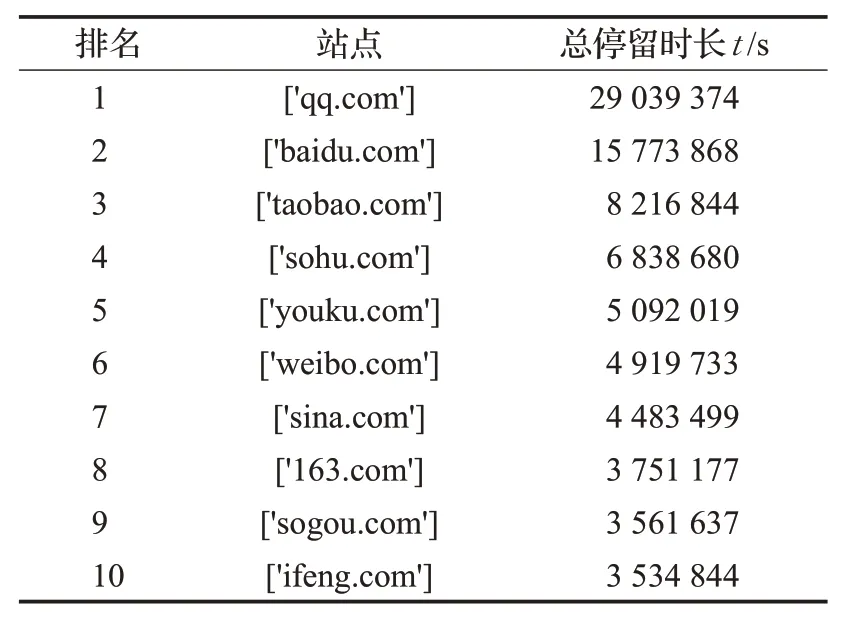
表2 站点总停留时长前10排名Table 2 Top 10 websites for total length of stay

3.3 注意力流网络异构性分析

根据注意力流网络结构熵算法ANSE，实验分析注意力流网络结构熵。在注意力流网络中，基于整体网络结构异构性的度量，注意力流网络结构熵算法ANSE综合考虑了站点的度值大小、停留时间、站点的总流量等，以站点的综合力为度量网络异构性更为准确，在本文实验中记吴结构熵为Wu结构熵，注意力流网络结构熵为Ha结构熵，度分布熵为Du度分布熵，蔡SD结构熵为SD结构熵。

在注意力流网络中，节点数为20 746个，不同边值的节点数量为280个，按照度分布熵模型，Du度分布熵最大值5.634，随着相同度值节点数的增加，网络度分布熵值也也会逐渐变小，当20 746个节点全加入时，Du度分布熵达到了最小2.491。因此，依据注意力流网络的结构特征，用度分布熵来度量注意力流网络的异构性是不准确的。其中蔡SD结构熵结合度分布熵和吴结构熵，单一地考虑节点和边，因此度量注意力流网络中也是不准确的。

分析注意力流网络的结构特征，适合用吴结构熵和注意力流网络结构熵来度量注意力流网络的异构性。通过实验得到网络结构熵值如表3所示，Wu结构熵值为7.875，Ha结构熵值为6.579，在该注意力流网络中Ha结构熵小于Wu网络结构熵，网络结构熵值越小，注意力流网络越混乱，意味着网络各部分间的差异越大，异构性越强。因此，从网络整体结构熵分析，注意力流网络结构熵能更好地度量网络的异构性。

表3 网络结构熵对比Table 3 Comparison of network structure entropy

3.4 站点差异性分析

分析发现，采用熵值算法计算单个站点的熵值，利用注意力流网络结构熵模型，站点的综合力越大站点熵值越大，所有站点的熵值如图5所示，最大从0.135依次降低，到最后站点时熵值接近0；利用Wu结构熵模型，结果如图6所示，随着站点的综合力降低站点熵值也基本整体依次降低，但有个别站点存在前一站点熵值高的情况。图7为排名前30的Ha和Wu结构熵站点熵值对比。例如sogou.com的Wu熵值为0.075 5，taobao.com站点Wu熵值为0.047 2，按照注意力流网络站点综合力的比较taobao.com站点要比sogou.com站点值大，Wu结构熵只考虑站点的度值的大小，说明Wu结构熵在刻画注意力流网络站点的差异性时存在不足。因此，注意力流网络结构熵能够很好度量网络站点的差异性。

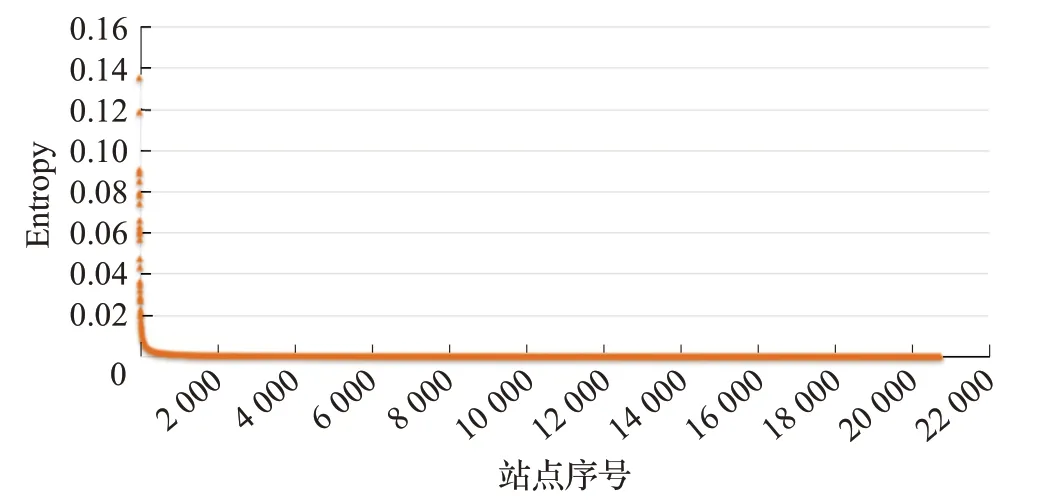
图5 Ha结构熵站点熵值Fig.5 Entropy of Ha structure entropy websites

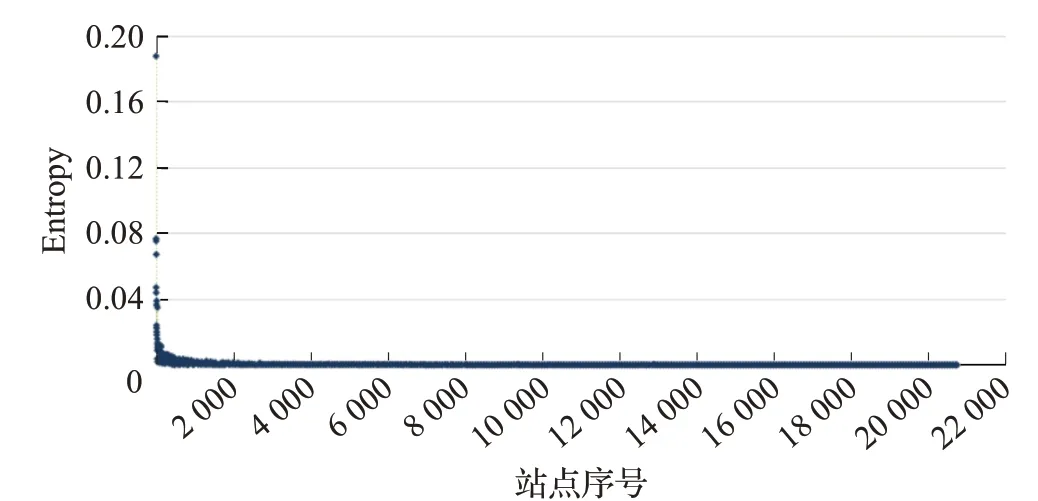
图6 Wu结构熵站点熵值Fig.6 Entropy of Wu structure entropy websites

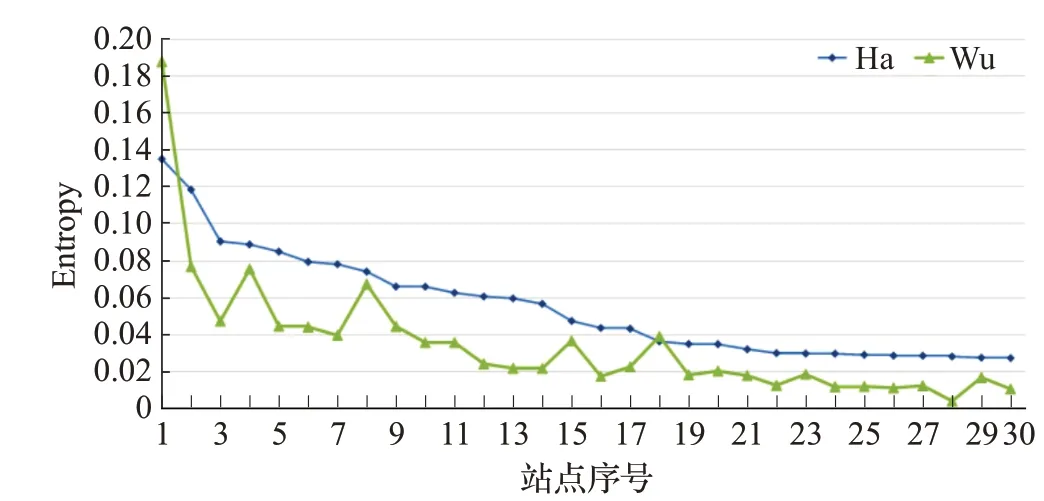
图7 Ha和Wu结构熵站点熵值对比Fig.7 Comparison of entropy values of Ha and Wu structure entropy websites

表4 各种站点重要性算法排名前15的站点Table 4 Top 15 websites ranked by various website importance algorithms

以上实验分析得出，Web站点之间有着很大的差异，注意力流网络结构熵能够更准确衡量站点的重要性，利用注意力流网络结构熵进行节点重要性排序分析，站点的Ha结构熵值越大，说明站点越重要，站点的影响力越大。在构建的注意力流网络中用ANSE算法和经典的节点重要性算法对比分析，分别和度中心性DC、中介中心性BC、接近中心性CC、特征向量中心性EC、PageRank对比分析。

表4显示了各种站点重要性算法排名前15名的站点。用各种算法的站点排名和中国的Alexa排名对比（Alexa排名是指网站的世界排名，是当前较为权威的网站综合排名评价指标。），本文提出的算法和Alexa排名更加接近一致，其他传统算法和Alexa排名有差异。在各种算法前15排名中，站点基本一致，但站点排名却不同，因此，说明本文算法的有效性和优越性，能够更好地度量站点的影响力。

实验得出，本文提出的注意力流网络结构熵模型的熵更小，能够更好地度量网络异构性；在站点重要性排名方面，本文提出算法排名更接近Alexa排名，ANSE算法能够有效度量网络站点的重要性。

4 结束语

本文利用在线点击上网行为数据，构建注意力流网络，分析注意力流网络结构，基于网络结构熵研究注意力流网络的异构性。针对注意力流网络的结构特征，传统的网络结构熵不能定量地度量注意力流网络的异构性，本文构建了基于注意力流网络的结构熵模型，提出了注意力流网络异构性度量算法ANSE，通过实验分析对比，本文提出的注意力流网络结构熵综合地从网络的站点度、停留时间等因素，能够更好地刻画注意力流网络的异构性。实验表明，站点的注意力流网络结构熵值越大，其站点越重要，站点的影响力越大。依据注意力流结构熵站点重要性排序，分别和经典节点重要性算法度中心性DC、中介中心性BC、接近中心性CC、特征向量中心性EC、PageRank对比分析发现，结构熵能更好地度量注意力流网络中站点的重要性，有效地分析站点差异性，为站点影响力排名提供理论依据，该研究可应用于社区发现、网络舆情监控、个性化推荐、广告精准投放等方面。