矩形路网结构对交通系统性能的影响
吴超云,郝庆一
(安庆师范大学数理学院,安徽 安庆 246133)
城市交通系统路网结构一般分为方格路网、环形放射路网、自由路网和混合路网[1-2]。交通系统路网结构是城市交通性能的一个重要因素,各种交通路网结构各有优缺点,结构不同交通性能也不同,一般采用交通路网可达性系数、非直线系数和路网连结度指数3个指标对交通系统路网结构进行综合评价[3-4]。
宏观基本图(MFD)是指整个交通系统路网的平均密度与平均流量之间的关系,可以从宏观层面上预测交通系统路网的运行状态,以及评价交通系统的性能[5]。2008年,文献[6]统计和分析了日本横滨出租车的数据,将整个城市交通系统的流量、占有率、密度和速度进行平均后,得到一个单峰的且离散度很小的曲线,首次证实了城市交通系统宏观基本图的存在性。2009年,文献[7]统计了法国图卢兹城市交通路网和高速公路路网的交通数据,发现宏观基本图会出现顺时针磁滞现象,并指出城市网络类型和拓扑结构影响宏观基本图的形状。2010年,姬杨蓓蓓等统计分析了荷兰阿姆斯特丹的交通数据[8],指出当交通系统中车辆密度分布均匀时,宏观基本图分散性较低。2011年,GEROLIMINIS等统计了美国明尼苏达州高速公路的交通数据[9-10],证实了高速公路网络也存在宏观基本图,并且在宏观基本图中出现了顺时针磁滞现象。2012年,朱琳等模拟了北京西三环路网及其子路网[11],结果显示不同规模和结构的交通系统路网的宏观基本图相差较大。2014年,贺正冰等统计分析了北京快速环路的交通数据[12],发现北京的宏观基本图出现磁滞现象。之后,许多学者对宏观基本图的存在性和相关理论进行了研究[13-17],其相关理论在交通分析、交通管理和交通控制等领域得到广泛应用[18-21]。
综上所述,当前交通路网结构对宏观基本图影响的研究较少,一般都是采集实测数据进行研究,没有探究交通路网结构对宏观交通流的影响。本文设计了一个长宽比可调的城市交通系统,保持矩形交通系统路网的总面积不变,模拟了不同长宽比的矩形城市交通路网对宏观交通流的影响。
1 矩形路网系统结构模拟的相关设置
利用NASCH元胞自动机模型[22],在开边界条件下,分别采用地理最短路径选择(TSP)策略和时间最短路径(GSP)策略,微观模拟矩形交通系统路网的交通性能。
1.1 矩形系统路网结构
建立M行N列的矩形交通系统路网,假设路网的总面积固定为M×N=144,则路网中有(M+1)×(N+1)个交叉路口和(M+1)×N+M×(N+1)条路段,每条道路有4条车道,每个路口都有红绿灯。当M=N=12时,路网为正方形交通系统路网。将长宽比定义为r=N/M,当长宽比越大时,路网结构越偏离正方形路网。
1.2 NASCH元胞自动机模型
在NASCH模型中,道路被划分为若干个离散元胞,每个元胞被1辆车占据或者为空元胞(没有车辆占据)。每辆车的速度可取[0,vmax]中的整数值,xi和vi分别表示第i辆车的当前位置和速度,pr是随机慢化概率。di=xi-xi+1-l表示第i辆车与前车之间的空元胞数量,其中l表示车辆长度,为车辆所占的元胞数量。本文设置l=1,pr=0.2,vmax=3,车辆的速度和位置并行更新,并给出如下更新规则:
(1)加速,vi=min(vmax,vi+1);
(2)减速,vi=min(di,vi);
(3)随机慢化,vi=max(vi-1,0),车辆以概率pr随机慢化;
(4)车辆运动,xi=xi+vi,车辆按照调整后的速度行驶。
1.3 路径选择策略
驾驶员最常用的路径选择策略是地理最短路径策略和时间最短路径策略。在GSP策略中,驾驶员选择总行程最短的路径前往目的地;在TSP策略中,驾驶员选择总旅行时间最短的路径前往目的地。
1.4 开边界条件
开边界条件下车辆以指定的加载比率β进入道路系统。初始状态下,城市交通系统路网中没有车辆,在每个时间步,车辆以加载比率β从每条道路最右侧车道进入交通路网,当车辆到达目的地后则离开路网。
在模拟实验中,每个时间步为1 s,模拟时间总计1 200 min,加载比率β每30 min变化一次(1 800个时间步)。图1描述了3种不同加载比率β的变化过程,模拟早高峰和晚高峰的城市交通状况。采用GSP策略时,车辆加载比率的最大值分别为0.034、0.025、0.023;而采用TSP策略时,车辆加载比率的最大值分别为0.040、0.034、0.030。为了对GSP策略和TSP策略进行比较,GSP第1种加载比率序列与TSP第2种相同。
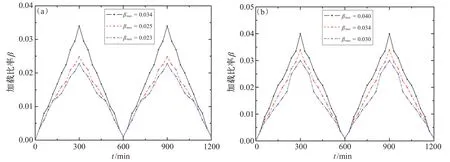
图1 加载比率β与时间的关系。(a)GSP策略;(b)TSP策略
1.5 模拟说明
文献[23-24]模拟了封闭边界条件下,分别采用GSP和TSP策略时,系统密度ρ与对应的车辆到达率A(每秒到达目的地的车辆数的均值,单位:vh)的关系,分别如图2(a)、2(b)所示。在封闭边界条件下,交通系统中的车辆数量保持不变,正方形路网的到达率峰值最大,但拥堵密度最低。随着长宽比r的增大,最大到达率减小,但拥堵密度增加。
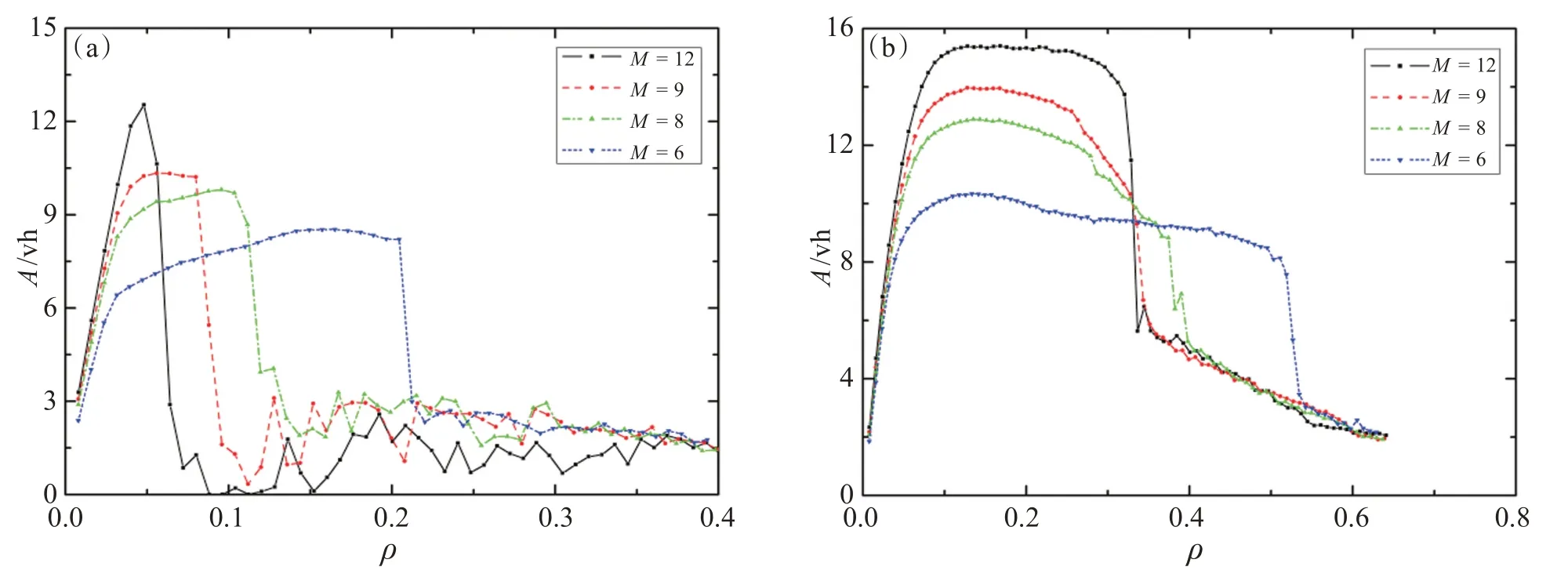
图2 封闭边界条件下,系统密度ρ与车辆到达率A的关系。(a)GSP策略;(b)TSP策略
基于元胞自动机模型,在开边界条件下,采用GSP和TSP策略微观模拟矩形城市交通系统对宏观交通流的影响,每5 min统计以下4个交通参数:系统密度ρ(5 min内每个时间步系统密度的平均值,无单位)、平均旅行时间T(5 min内所有到达目的地的车辆从源点到目的地所经历时间的平均值,单位:s)、平均速度V(5 min内每个时间步系统中所有车辆速度的平均值,单位:cells/s)、平均交通流量J(5 min内每个时间步交通流量的平均值,单位:vh/s)。系统密度表示系统中的车辆数量与系统可容纳的车辆数量的比值,交通流量表示每个时间步经过道路中间某点的车辆数。在GSP和TSP策略下,对不同的加载比率,分别进行模拟实验,每组加载比率模拟50次,然后对上述4个交通参数再取平均值。
2 GSP策略的模拟结果及分析
图3~图5为GSP策略下不同加载比率的实验结果。由图3可见,在βmax=0.034时,这4种矩形结构路网在早高峰结束时都处于堵塞状态。车辆数持续增加导致交通系统堵塞。即使在没有车辆进入系统时,堵塞也不会消失,因为此时车辆到达率非常低,系统密度只有小幅度下降,且当晚高峰开始时,系统密度迅速增加并接近1.0,此时系统陷入全局死锁状态。
在图3(a)中,同一时刻,随着长宽比r的增加,系统密度迅速增大。这是因为在系统密度较低时,随着长宽比r的增加,车辆到达率低(图2(a))。又因车辆到达率低于进入系统的车辆数,故路网中系统密度逐渐增加。由于加载比率相同,长宽比大的路网车辆到达率低,所以交通密度增长更快。在300 min时,路网密度分别为0.219、0.350、0.361、0.478,此时系统密度比临界堵塞密度大很多,而车辆到达率很低,导致系统密度越来越大,最终进入死锁状态。
交通系统密度增加,平均旅行时间单调增加(图3(b)),而平均速度单调减小(图3(c)),所有交通系统的宏观基本图都进入拥塞段(图3(d))。
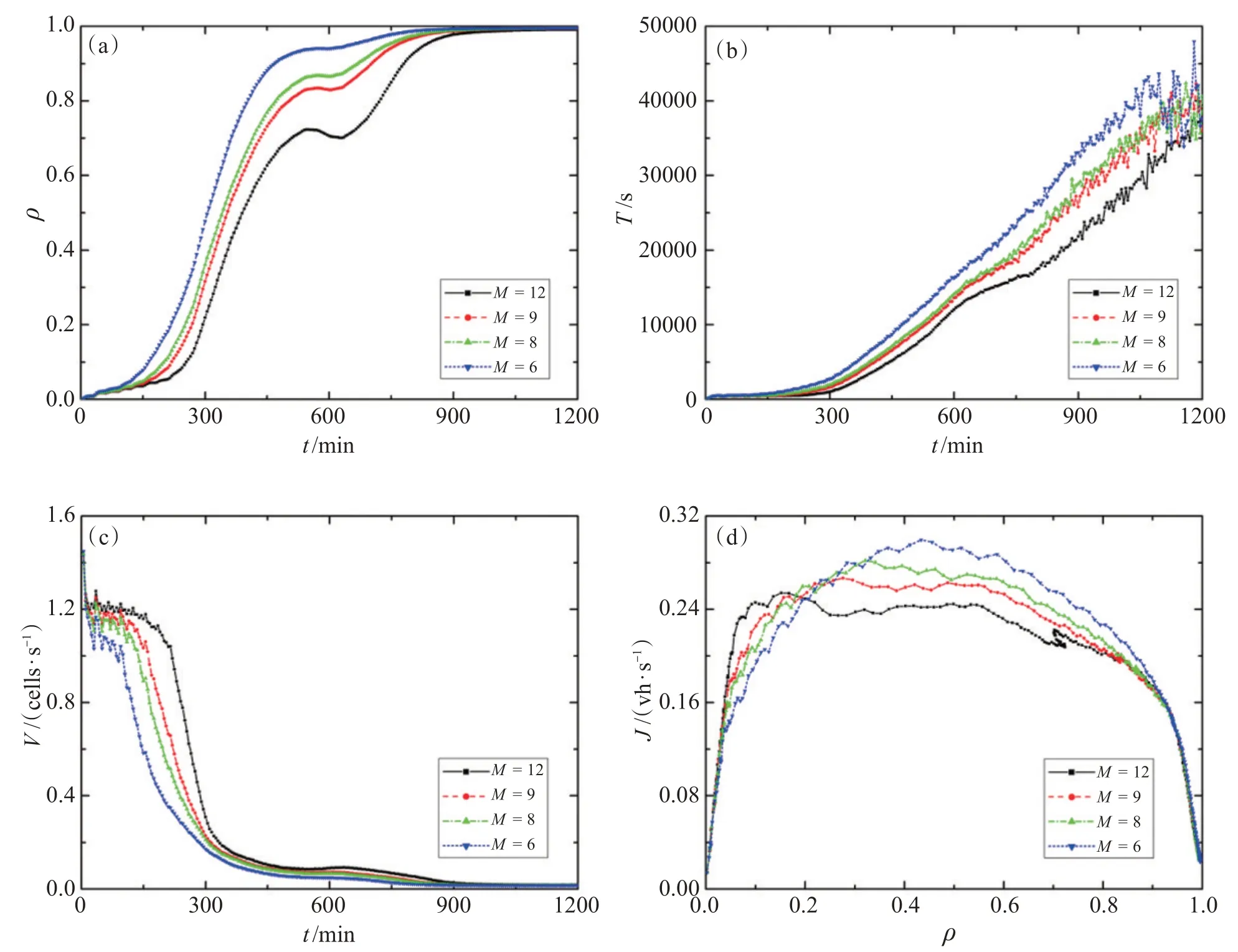
图3 开边界条件下,采用GSP策略在βmax=0.034时的系统性能
图4为βmax=0.025时GSP策略的交通性能。此时,长宽比较小的路网显示出更好的性能,而长宽比最大的路网(M=6,r=4)会导致系统陷入死锁状态(图4(a))。正方形路网(M=12,r=1)交通性能最佳,此时系统密度最低(图4(a))、平均旅行时间最低(图4(b))、车辆平均速度最高(图4(c))。这是因为正方形路网在低密度时具有更高的到达率(图2(a))。在图4(b)中,对于所有4个交通路网,平均旅行时间T=600 min时达到最大值,该时间点也对应达到最小速度的时间(图4(c))。在图4(d)中,M=6时系统路网的宏观基本图进入拥塞段,M=8、9、12这3个长宽比较小的路网的宏观基本图保持在低密度区域。宏观基本图中出现明显的磁滞现象,表明卸载过程中的交通流量比加载过程的交通流量更低。

图4 开边界条件下,采用GSP策略在βmax=0.025时的系统性能
图5显示了βmax=0.023时的系统性能,此时所有系统都运行良好。在加载过程中,M=12的正方形路网的系统密度最低、平均旅行时间最低且平均速度最高,系统性能最好。路网M=6的系统密度最高、平均旅行时间最高且平均速度最低,系统性能最低(图5(a)~5(c))。在图5(d)中,M=12的正方形路网的宏观基本图中磁滞环几乎消失,M=6、8、9的交通路网仍呈现明显的磁滞现象。
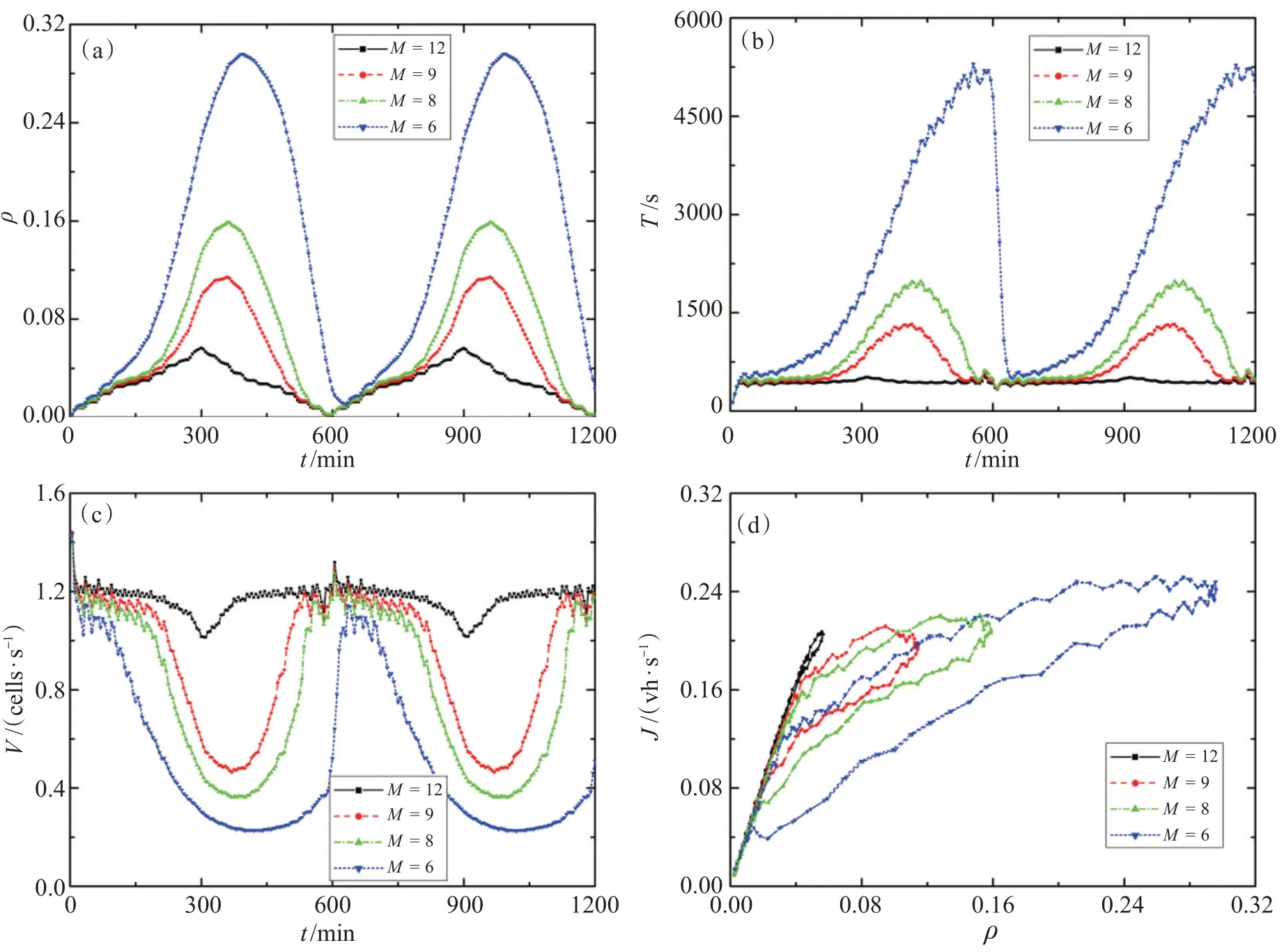
图5 开边界条件下,采用GSP策略在βmax=0.023时的系统性能
3 TSP策略的模拟结果及分析
图6~图8是开边界条件下采用TSP策略的模拟结果。
与GSP策略类似,在较高的交通负载情况下,即βmax=0.040时,随着长宽比的增加,系统密度更快接近于1(图6(a)),平均旅行时间增长速度更快(图6(b)),平均速度更低(图6(c))。4种交通系统最终都进入死锁状态,宏观基本图也都进入拥塞段(图6(d))。
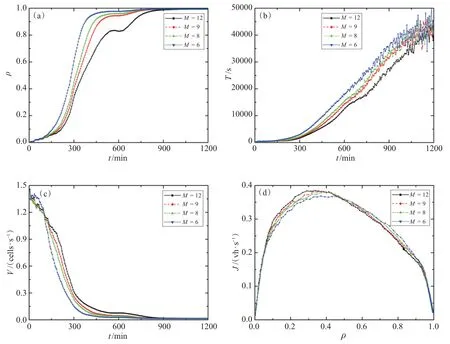
图6 开边界条件下,采用TSP策略在βmax=0.040时的系统性能
图7展示了中等交通负荷(βmax=0.034)的模拟结果。从图7(a)看出,只有M=6的交通路网出现堵塞,M=8、9、12这3个路网运行良好。M=8、9、12的路网在模拟结束时,系统密度都接近于0,满足交通需求。随着长宽比增加,系统密度更高(图7(a)),平均旅行时间更长(图7(b)),平均速度更低(图7(c))。M=6时,路网的宏观基本图进入拥塞段,M=8、9、12的路网的宏观基本图则出现磁滞现象。随着长宽比的增加,相同密度对应的交通流量降低,磁滞环增大,如图7(d)所示。
比较GSP策略(图3)和TSP策略(图7)的模拟结果,此时两者的加载比率相同,显然TSP策略明显优于GSP策略。在相同交通需求下,GSP策略将导致4个交通系统都堵塞,而TSP策略在长宽比低的3个系统中表现良好。M=6时,TSP策略的系统密度也低于GSP策略。低交通负载(βmax=0.030)的模拟结果如图8所示,4个交通系统都运行良好。系统密度、平均旅行时间、平均速度和宏观基本图的规律与βmax=0.034时的情况类似。由于加载比率更低,所以车辆分布更均匀,相同路网的宏观基本图的磁滞环更小(图7与图8)。可以预计,随着加载比率β的降低,磁滞现象都将消失。

图7 开边界条件下,采用TSP策略在βmax=0.034时的系统性能

图8 开边界条件下,采用TSP策略在βmax=0.030时的系统性能
4 总结
城市交通系统的结构对交通系统性能影响很大,本文研究了不同长宽比的矩形结构城市交通系统路网对交通性能的影响。在开边界条件下,考虑了GSP和TSP策略,从系统密度、平均旅行时间、平均速度、宏观基本图(流量-密度关系)等方面分析了交通系统的性能。在开边界条件下,正方形路网拥有更好的交通效率,而长宽比越大,交通系统性能越低。

