约束不足的杆、梁静变形的定性性质

王其申，王大钧，何北昌

（1.安庆师范大学数理学院，安徽安庆246133；2.北京大学工学院湍流与复杂系统国家重点实验室，北京100871；3.Consulting Seattle，WA，USA)

文献[1-2]阐明了充分约束的杆和梁具有静变形振荡性质A和B，它们在阐述相应系统具有振动的振荡性质方面起到了重要作用。实际工程问题中存在大量约束不足的系统，这类系统是否也具有静变形振荡性质？如果是，那么在这类系统中，静变形振荡性质A和B的陈述是否需要加以改变？这就是本文所要回答的两个问题。

1 两端自由杆的静变形振荡性质

杆的约束不足系统只有一种支承方式，即两端自由的直杆。对于两端自由的杆，下面将证明它具有如下的静变形振荡性质A和B。需要说明的是，本文以下讨论的杆可以是变截面的，但一定存在纵向对称轴，下面所称的轴力，必沿杆的纵向对称轴作用。

性质A两端自由杆在一对平衡轴向外力作用下，其任意横截面的形心的轴向位移仅发生一次正负号改变。

性质B两端自由杆在一组n个轴向外力组成的平衡力系作用下，其任意横截面的形心的轴向位移发生正负号改变的次数（以下简称符号改变数）不超过n-1。

为了证明上述静变形振荡性质，需要给出如下两个命题。

命题1设φ′(x)在区间[a,b]上连续且以(i=1,2,3,…,n)为其自左至右顺序排列的节点而无别的零点，则φ(x)在子区间内至多各有一个零点，从而φ(x)在(a,b)内最多共有n+1个零点。如果

命题2设φ′(x)在区间[a,b]上分段连续且以(i=1,2,3,…,n)为其自左至右顺序排列的可能的变号点，而在每个子区间内正负号不变，则命题1的结论同样成立。

命题2显然只是命题1的推广，它们的证明可以参看文献[2]的引理5.4，这里从略。

性质A的证明考察图1所示自然长度为l的两端自由杆，取未受外力从而未发生变形时的左端点为坐标原点，其纵向对称轴为x轴。设在其上d1、d2两处杆受到一对平衡轴向外力F1和F2=-F1的作用，这里0≤d1＜d2≤l。显然，杆上各点的位移必为其原始平衡状态时的各横截面的形心坐标x的函数，记为u(x)。考察0＜d1＜d2＜l的情况。在此种情况下，由材料力学可知，杆的变形方程和轴力分布为

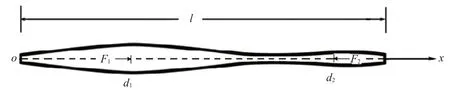
图1 两端自由杆的连续系统示意图

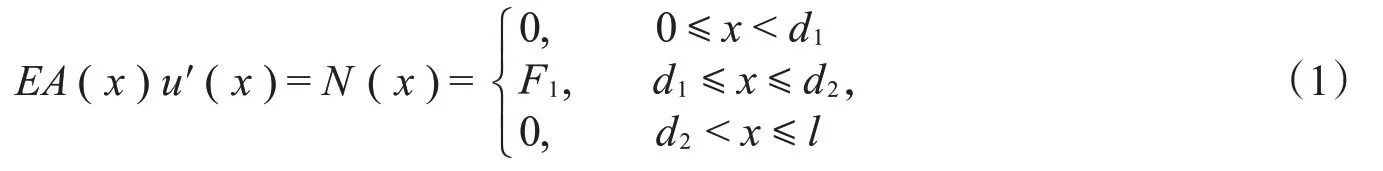
由此即有

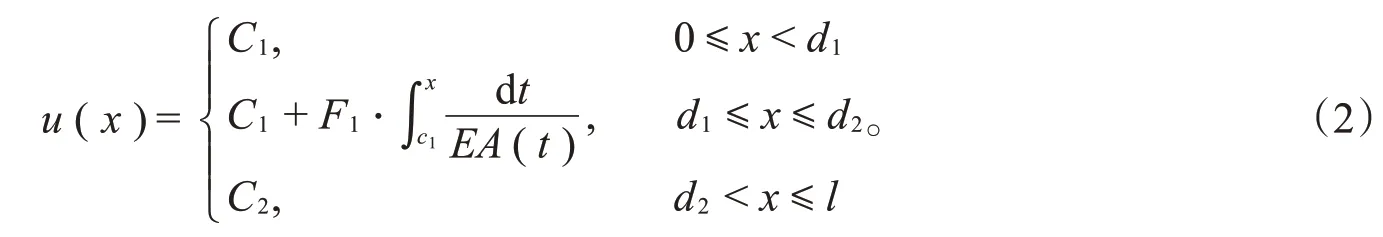
其中，C1和C2是两个积分常数。式（2）表明，u(x)只可能在区间(d1,d2)内出现正负号改变，注意到u′(x)在区间(d1,d2)内恒正或恒负，即u(x)在区间(d1,d2)内单调增或单调减，所以它最多只能改变正负号一次。由理论力学的质心运动定理可知，当一对平衡轴向外力在同时缓慢均匀加载时，两力作用点之间必存在某一横截面的位移为零，因而性质A成立。

对于d1=0或d2=l的情况，上述式（1）和式（2）的左或右端子区间将不存在，显然并不影响相应结论的成立，故性质A得证。

性质B的证明自然长度为l的两端自由杆坐标原点和x轴的取法同上。设在其上di处杆受到n个轴向外力Fi所组成的平衡力系作用，这里i=1,2,3,…,n并满足0≤d1＜d2＜…＜dn≤l。同样，杆上各点的位移仍为其原始平衡状态时的各横截面的形心坐标x的函数，记为u(x)。仍然先考察d1＞0和dn＜l的情况。此时，由材料力学可知，杆的变形方程和轴力分布为

所有试剂属分析纯，均未进一步纯化处理。红外光谱使用Nicolet Avatar360型红外光谱仪测定，溴化钾压片，4000-400cm-1波数范围扫描；元素分析是用Perkin-Elmer 2400Ⅱ型元素分析仪完成；TG热分析是在Perkin-Elmer-7热分析仪(空气气氛，升温速度10℃/min)上测定的。

式（3）表明，u′(x)只可能在外力作用点di(i=2,3,4,…,n-1)处出现正负号改变，而在d1和dn处没有正负号改变，从而u′(x)在区间(0,l)内改变正负号不多于n-2次。由命题2可知，u(x)在区间(0,l)内改变正负号不多于n-1次，即性质B成立。

对于d1=0或dn=l的情况，式（3）的左或右端子区间将不存在，显然并不影响结论的成立，故性质B得证。

2 约束不足梁的静变形振荡性质

由于梁的约束不足系统有多种支承方式，必须分别讨论。

2.1 一端铰支一端自由梁的静变形振荡性质

性质A一端铰支一端自由梁受到一对横向外力作用，且当这对横向外力与其铰支端的支反力组成一个平面平衡力系时，则梁的挠曲线的正负号改变不超过1次。

性质B一端铰支一端自由梁在受到一组n个横向外力作用，且当这组横向外力与其铰支端的支反力组成一个平面平衡力系时，则梁的挠曲线发生正负号改变的次数不超过n-1次。

证明首先，当长为l的一端铰支一端自由梁仅受一对集中外力作用时，无论外力作用点d2是否重合于自由端，由材料力学可知，其挠曲线如图2所示，显然挠曲线的正负号改变数不超过1，即静变形振荡性质A成立。

图2 一端铰支一端自由梁受一对横向外力作用时挠曲线的两种情况

其次，考察一端铰支一端自由梁在其上di(0＜d1＜d2＜…＜dn≤l)处受n个集中外力作用时的挠度u(x)的正负号改变次数。如果dn＜l，由材料力学可可知，u(x)满足以下剪力方程：

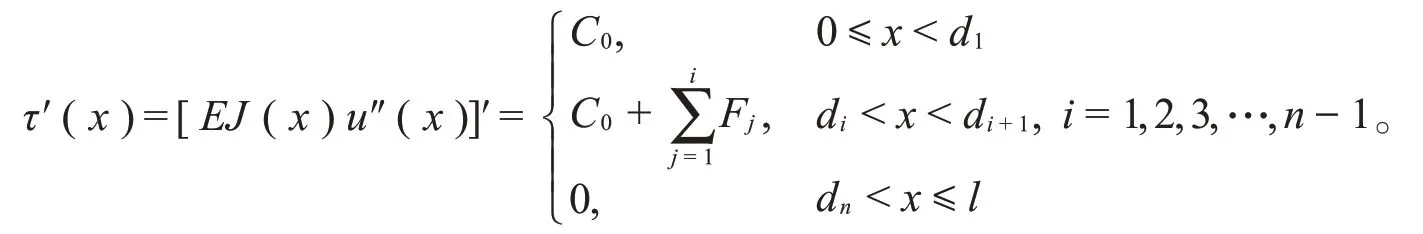
上式表明，τ′(x)最多只在外力作用点处di(i=1,2,3,…,n-1)改变正负号一次，从而其变号数不超过n-1。在一端铰支一端自由的情况下，τ(0)=τ(l)=0，由命题2可可知，τ(x)在区间(0,l)内的变号数不超过n-2；由命题1可知，相应的u′(x)和u(x)在区间(0,l)内的变号数不超过n-1和n。但因u(0)=0，将使u(x)在区间(0,l)内的变号数减少1，这样，u(x)在区间(0,l)内的变号数不超过n-1。

如果dn=l，梁的最后一个分段(dn＜x≤l)不存在，显然这不影响上面的讨论。因此，一端铰支一端自由梁的挠度在其跨度范围内的变号数不超过n-1，即静变形振荡性质B成立。

2.2 一端滑支一端自由梁的静变形振荡性质

性质A一端滑支一端自由梁受到一对横向外力作用，且当这对横向外力与其滑支端的支反力偶组成一个平面平衡力系时，则梁的挠曲线的正负号改变不超过1次。

性质B一端滑支一端自由梁在受到一组n个横向外力作用，且当这组横向外力与其滑支端的支反力偶组成一个平面平衡力系时，则梁的挠曲线变号数不超过n-1。

一端滑支一端自由梁的静变形振荡性质A同样可以通过画出它的挠度示意图验证，只是注意这种情况下，u′(0)=τ′(0)=0，这里从略。

当一端滑支一端自由梁在其上di(0≤d1＜d2＜…＜dn≤l)处受n个集中外力作用时，如果d1＞0和dn＜l，由材料力学可知，其挠度函数u(x)满足以下剪力方程：

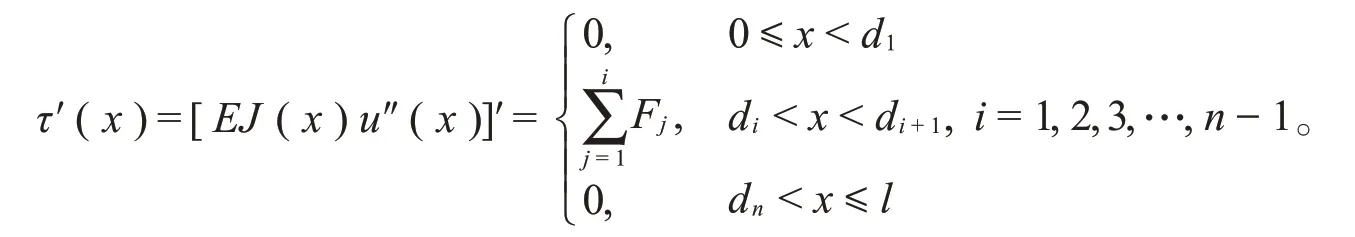
上式表明，τ′(x)最多只在外力作用点处di(i=2,3,4,…,n-1)改变正负号一次，从而其变号数不超过n-2。在一端滑支一端自由的情况下，τ(l)=0，由命题2可知，τ(x)在区间(0,l)内的变号数也不超过n-2；因u′(0)=0，由命题1可知，相应的u′(x)和u(x)在区间(0,l)内的变号数不超过n-2和n-1。

如果d1=0或dn=l，梁的首尾分段0≤x＜d1或dn＜x≤l不存在，仍然不影响上述讨论。因此，一端滑支一端自由梁在其跨度范围内的变号数不超过n-1，即静变形振荡性质B成立。

2.3 两端滑支梁的静变形振荡性质

性质A两端滑支梁受到一对横向外力作用，且当这对横向外力与其两个滑支端的支反力偶组成一个平面平衡力系时，则梁的挠曲线的正负号改变不超过1次。

性质B两端滑支梁在受到一组n个横向外力作用，且当这组横向外力与其滑支端的支反力偶组成一个平面平衡力系时，则梁的挠曲线变号数不超过n-1。

两端滑支梁的静变形振荡性质A和B可以完全类似于一端滑支一端自由梁的情况予以证明，只是需要注意该情况下，u′(0)=τ′(0)=0，u′(l)=τ′(l)=0，因此它的剪力τ′(x)、弯矩τ(x)、转角u′(x)和挠度u(x)的变号数分别不超过n-2、n-1、n-2和n-1。具体讨论这里从略。

2.4 两端自由梁的静变形振荡性质

性质A两端自由梁受到三个横向外力作用，且当这组横向外力组成一个平面平衡力系时，则梁的挠曲线的正负号改变不超过1次。

性质B两端自由梁在受到一组n个横向外力作用，而这组横向外力组成一个平面平衡力系时，则梁的挠曲线变号数不超过n-1。

两端自由梁的静变形振荡性质A仍然可以通过画出它的挠度示意图来验证，这里从略。

注意到两端自由梁的边界条件τ(0)=τ′(0)=0，τ(l)=τ′(l)=0，利用命题1和命题2，可以发现它的剪力τ′(x)、弯矩τ(x)、转角u′(x)和挠度u(x)的变号数分别不超过n-2、n-3、n-2和n-1。

3 结论

以上给出了约束不足的杆和梁的静变形振荡性质。推理发现，对于约束不足的系统，要讨论它的静变形，所施加的外力系必须是平衡外力系；而有关性质A的表述显然与充分约束系统不尽相同；但有关性质B的表述，其结论部分与充分约束系统则是完全一致的。该研究结论也可以扩展到约束不足的杆、梁离散系统。