开圆孔单角钢构件稳定承载力分析
吴海兵,叶爱民,白 强,王松涛
(中国电力工程顾问集团中南电力设计院有限公司,湖北 武汉 430071)
0 引言
角钢构件广泛应用于输电格构式塔架中,失稳是其作为压杆的主要破坏模式。由于缺陷的客观存在,角钢的失稳呈极值型,GB 50017—2017《钢结构设计标准》(以下简称钢标)中,考虑了1/1 000 杆长的初弯曲和残余应力两种缺陷对压杆稳定承载力的影响[1]。
但在输电铁塔角钢构件上除了上述两种缺陷,还可能存在辅助抱杆孔、接地孔等孔洞缺陷。此外,在既有线路的改造加固项目中,也可能因改变节间布置而导致原构件节点上的约束孔变为非约束孔。
国内外学者对冷弯薄壁型钢构件开孔承载力的研究[2-5]结果表明,孔洞对构件稳定承载力存在不容忽视的削弱效应。某工程铁塔真型试验中也曾出现过构件在辅助抱杆孔处发生破坏的现象,如图1所示。

图1 某工程铁塔真型试验开孔构件破坏
国内外钢结构设计相关规范[1,6]仅考虑孔洞缺陷对角钢构件强度的削弱,而忽视了其对构件受压稳定承载力的影响。冷弯薄壁型钢领域虽有相关研究,但由于冷弯薄壁型钢与轧制型钢的屈曲模式不同,其研究结论无法直接应用。
由于缺乏设计理论和规范的指导,设计人员难以准确把握孔洞对角钢轴压构件承载力的影响,这给输电线路的设计和运行造成了一定的安全隐患。本文借助有限元软件ANSYS,探讨开圆孔对单角钢轴心受压构件极限承载力的影响。
需要说明的是,本文仅讨论构件中间非约束孔洞对其稳定承载力的影响,对连接节点处的螺孔,因其在变形时属于支座,对构件的稳定不产生实质影响,故不做讨论。
1 有限元计算
1.1 有限元模型
模型采用三维8 节点实体单元SOLID185 建模,该单元可考虑弹塑性和大变形,适用于存在局部开孔等特殊构造的精细化有限元分析。
计算假定与钢标保持一致:钢材本构采用理想弹塑性模型,弹性模量取E=206 GPa;杆件端部约束为两端铰接;不考虑初偏心和杆件自重的影响;初始缺陷考虑1/1 000 杆长初弯曲和截面残余应力;残余应力分布为肢中部拉应力,边缘压应力,峰值取为Q235 钢材屈服强度的20%[7-8],沿杆长各截面分布相同。
有限元模型如图2 所示,为模拟构件的两端铰接约束,采用多点约束(MPC)技术,在模型两端各添加一个参考点,分别与角钢两端截面耦合,约束和荷载均施加在相应的参考点上。为尽可能准确地模拟孔边的应力状态,对开孔局部进行了网格加密。

图2 构件开孔的有限元模型
1.2 破坏模式
开孔角钢轴压构件极限状态下的典型应力云图如图3 所示,其破坏模式表现为与无孔构件类似的绕截面最小轴的整体弯曲屈曲。与无孔构件不同的是,圆孔的应力集中效应导致在加载过程中,孔边的部分单元率先屈服,从而削弱了开孔截面处的截面刚度,导致构件屈曲时最大变形可能出现在开孔截面而非跨中截面处,构件的承载力也较无孔构件有所降低。
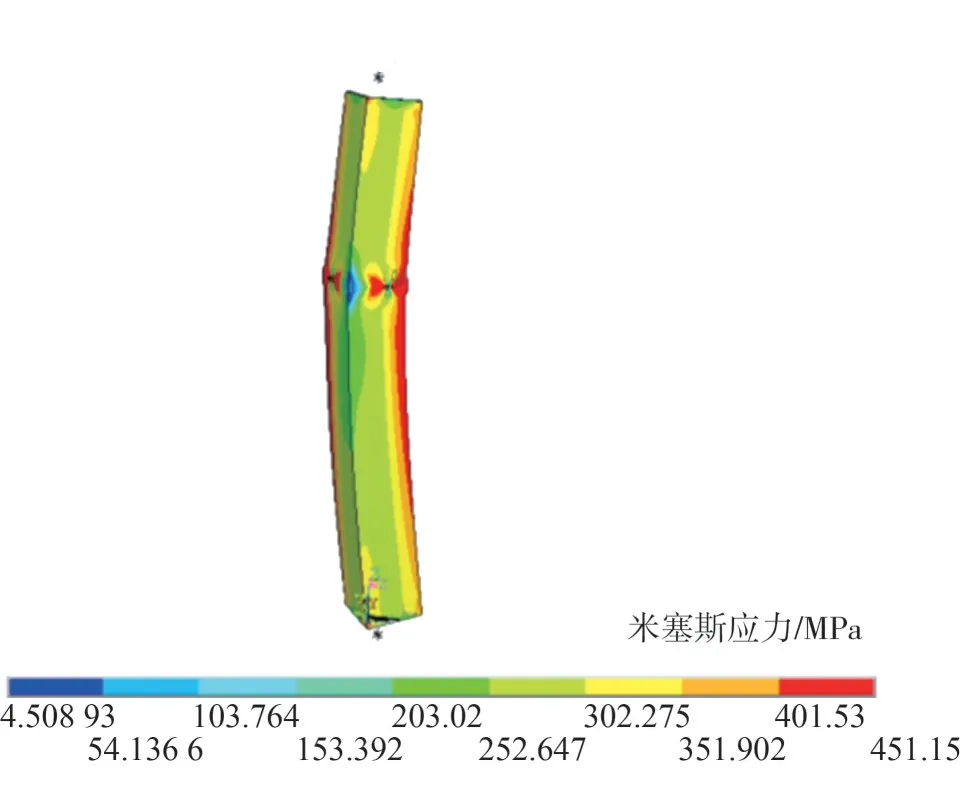
图3 开孔角钢轴压构件的典型应力云图
2 参数分析
孔洞对构件承载力的削弱效应与开孔位置、大小、构件长细比等多种因素相关。为定量研究各因素的影响,考虑到输电线路孔洞缺陷一般出现在主材上,选取主材规格、构件长细比、孔端距、孔边距4 个参数为考察对象,每个参数取3个水平,共81个试件进行参数化有限元计算,角钢构件开孔参数示意如图4所示。
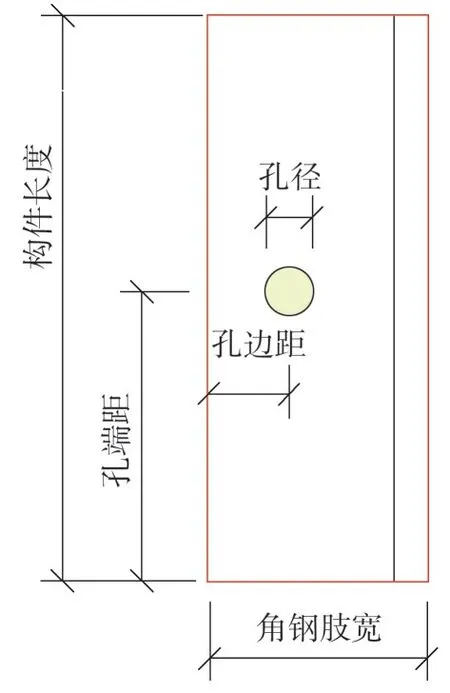
图4 角钢构件开孔参数
计算参数及结果如表1所示。
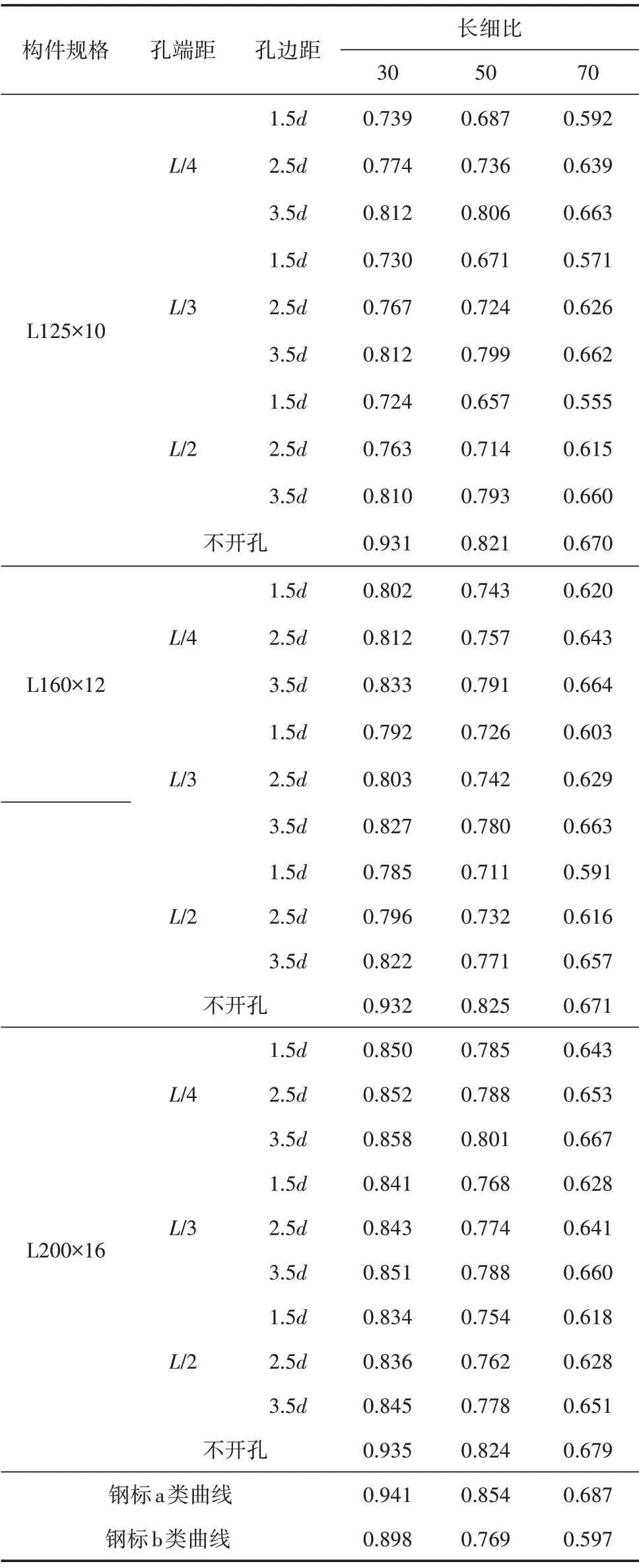
表1 开孔角钢构件稳定系数计算值
由表1可见:
1)不开孔角钢构件三种截面的稳定承载力计算值基本一致,与钢标a类曲线差异仅1%~3%,计算精度较好。
2)考虑按钢标对开孔构件进行净截面强度验算时,三种规格(从小到大)的净截面强度系数(净截面强度与毛截面强度之比)分别为(0.821,0.860,0.888),而其稳定系数计算值均小于净截面强度系数,可见仅验算开孔构件的净截面强度偏于不安全。
3)角钢构件开孔后,稳定承载力的最大降低幅度高达约18%。可见在设计中忽视开孔对构件稳定承载力的影响也存在一定安全隐患,尤其是按新钢标规定,将高强角钢视为a类截面时。
4)构件长细比、规格、开孔位置对其承载力的降低幅度均有一定影响。由于计算孔径始终不变,不同规格开孔后稳定系数的差异可理解为开孔大小的影响。
2.1 构件长细比的影响
不同长细比下,各开孔位置稳定系数降低幅度的平均值如图5所示。
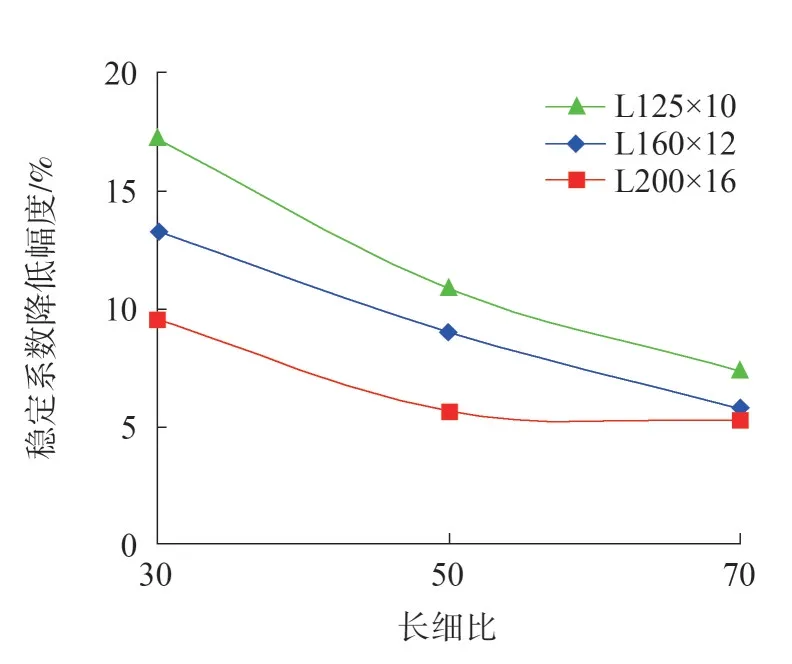
图5 构件长细比的影响
可见,长细比对开孔构件稳定承载力的影响较大,同一构件不同长细比下的稳定系数降低幅度极差达到4%~10%。长细比越小,开孔沿构件长度方向的相对范围越大,对构件稳定承载力的影响程度越高。
从变化趋势看,开孔对构件稳定承载力影响程度的变化幅度也随长细比的增大而逐渐降低,如L200×16 角钢,长细比从50 变化到70 时,稳定系数的降低幅度基本不变。
2.2 开孔大小的影响
不同规格下,各开孔位置稳定系数降低幅度的平均值如图6 所示。可见,长细比和开孔位置相同时,相对孔径越大,孔边应力集中的范围越大,构件的削弱越严重,稳定系数的降低幅度也越大,且开孔大小的影响随长细比的增加而逐渐减小。

图6 开孔大小的影响
2.3 开孔位置的影响
2.3.1 孔端距的影响
由图7 可见,不同长细比下,不同孔端距的构件稳定系数降低幅度变化规律基本相同。长细比为50时,不同孔端距下构件稳定系数的降低幅度如图7所示。

图7 孔端距的影响
可见,开孔离支座越近,构件稳定承载力降低幅度越小,开孔位于跨中时,稳定承载力最低。但不同孔端距稳定系数降低幅度的极差仅约4%,可见孔端距的影响并不显著。
2.3.2 孔边距的影响
由图8 可见,不同长细比下,不同孔边距的构件稳定系数降低幅度变化规律基本相同。长细比为50时,不同孔边距下构件稳定系数的降低幅度如图8所示。

图8 孔边距的影响
可见,开孔越靠近角钢肢尖,构件受压承载力降幅越大,且角钢规格越小,不同孔边距的降低幅度极差越大,孔边距的影响越大。
孔边距影响较为显著的原因,一方面是因为应力集中的位置靠近构件边界时,孔与边界的相互干涉会加剧应力集中程度[9],另一方面,开孔越靠近肢尖对截面的惯性矩削弱越大。
角钢的受压承载力与开孔位置关系密切,这也充分证明了不能简单将开孔对角钢承载力的影响视为强度问题。
2.4 开孔数量的影响
考虑到工程中常有构件单肢开孔或双肢开多个孔的情况,针对规格为L160×12,开孔端距为L/2 的构件,补充计算其仅在单肢开一个孔和在双肢上均开两个孔(孔中心距3d)的情况,结果如表2所示。
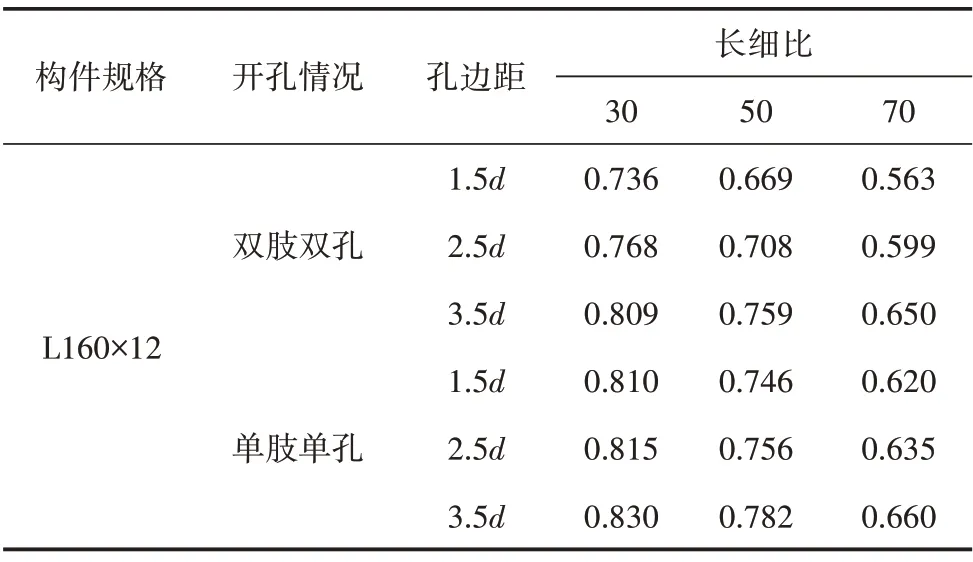
表2 不同开孔数量的角钢稳定系数计算值
各开孔数量下构件的稳定系数降低幅度如图9所示。
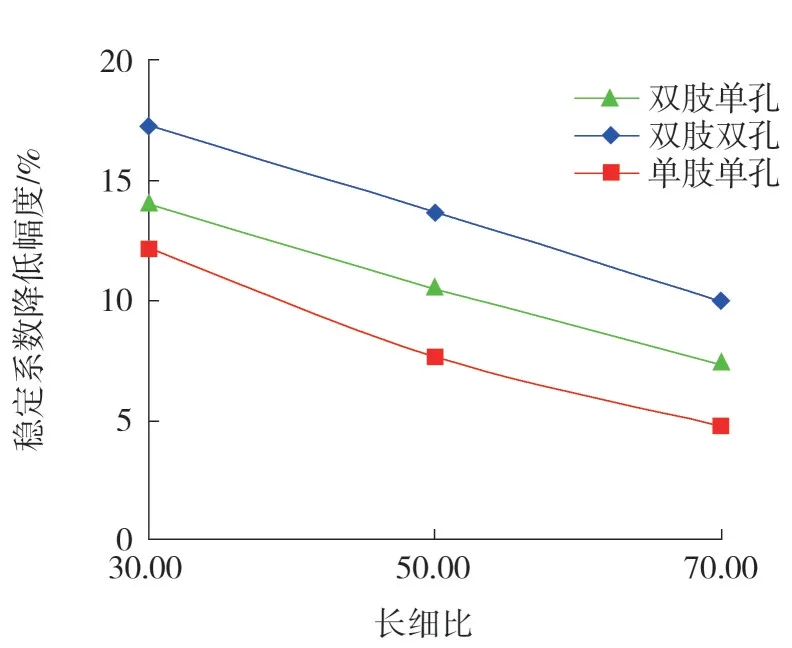
图9 开孔数量的影响
可见,沿杆件横截面方向和杆轴方向的开孔数量越多,对构件的削弱程度越大,构件稳定承载力的降低幅度也越大,且孔边距越靠近肢尖、长细比越小,开孔数量的影响越大。
3 结语
开孔将导致构件屈曲时应力和变形往孔边集中,构件屈曲时最大变形由跨中向开孔截面位置转移。
对受压强度控制的开孔构件(毛截面稳定承载力大于净截面强度),仅验算其净截面强度偏于不安全。
对受压稳定控制的开孔构件,开孔对构件稳定承载力的影响同样不容忽视。构件长细比、开孔大小、位置和数量均对角钢的稳定承载力存在一定影响。
长细比越大,开孔对构件承载力的影响越低;开孔越大、数量越多,构件承载力越低;开孔距角钢肢尖越近、距节点越远,构件承载力越低。
设计中建议尽量避免对受压构件开自由孔,否则应验算其稳定承载力,并尽量使开孔远离肢尖并靠近节点。

