密度分层对热射流流动的影响预测模型

毛德龙，王康硕，沙 江，何 凛，任海刚，王怡豪，王 奔

(中国船舶工业系统工程研究院，北京 100094)

0 引 言

水下航行体因其极强的隐蔽性与突袭性而在军用领域占有重要地位，其中以潜艇最具代表性[1]。近年来，受益于光电技术的飞速发展，红外探测设备的分辨率、精度和抗干扰能力大大提高，红外探潜作为一种重要的非声探潜措施，以其探测范围大、昼夜工作、被动探测等优点而被广泛关注[2-4]。水下航行体在航行过程中，其动力系统产生的废热会被冷却水吸收，并随冷却水排放到海水中。这些冷却水的温度明显高于周围水体的温度，在密度差的驱使下向上浮升，有可能在海面形成温度异常的红外特征。

目前，相关学者针对密度分层对热射流流动的影响进行了大量研究，并取得了一系列成果。江传富等[5]提出了热尾流不同发展阶段的物理模型，分析了其在密度均匀和分层流体中的浮升规律；张昊春等[6]建立了温度分层环境和均匀介质环境中的射流模型，计算得到了热尾流的温度分布特性及浮升扩散过程中的衰减规律；杨立等[7]通过对线性密度分层流体中热尾流的浮升过程研究，发现了流体的分层会抑制热尾流的浮升。

海水的温度分布受诸多因素的影响，如深度、地理位置、季节、太阳辐射和海洋大气热交换等。海水温度随深度的增加而显著递减，根据NOAA（National Oceanic and Atomspheric Administration）数据库WOD(World Ocean Database)可得海水温度沿着深度方向的变化规律[8]，不同纬度地区海水总体温度变化值约在30℃左右；同一地区，在50 m深度范围内，海水温度变化范围约在1℃～2℃，靠近海平面处（深度20 m以内）温度沿深度变化不明显，原因为海上风浪大，海平面处海水运动剧烈，不同深度海水之间对流混合，温度趋于一致；深度大于20 m后水温迅速下降。海水盐度是指海水中全部溶解固体与海水质量之比，也会随深度的变化而发生改变。根据海水温度、盐度在深度方向上的变化情况，总结了40° N附近50 m深度内，密度变化规律，如图1所示。在深度方向上，海水的密度为线性增加，50 m深度下密度的增长幅度为0.35‰。需要指出的是，大量文献中对表层海水密度分层的处理方式也是线性的，与图1中的规律有一致性[9,10]。

本文在海水密度沿深度方向变化规律的基础上，使用数值仿真手段模拟热射流在密度分层海水中的运动，探究密度分层对热射流流动的具体影响关系，矫正未分层情况下数值仿真的预测结果，增加数值仿真预测结果的可靠性。

1 数学模型

数值仿真采用流体连续介质模型假设，其流动受纳维斯托克斯（N-S）方程控制[11]。N-S方程的张量形式如下：

式中：fi为流体受到的体积力，此处为热射流受到周围冷流体浮力与重力的合力。

以温度形式表达的能量方程为：

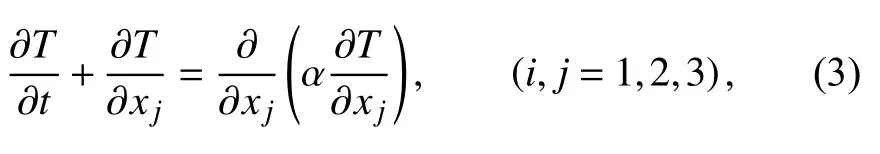
其中 α为热扩散率。根据Boussinesq假设，忽略密度变化在非稳态项、对流项和扩散项中的影响，即在上述3项中密度取常数，只考虑密度变化在浮力项中的影响。

密度与温度的关系式为：

式中：TRef为参考温度，取环境的水温，其他所有物质特性均取参考状态下的介质属性。

密度不分层情况下，Boussinesq假设参考密度ρRef是一个定值，其在空间中的分布是常数，而密度分层情况下 ρRef沿着深度方向是变化的。本文研究目的在于探究密度变化对热射流的影响，因此实际海水中的盐度与温度分层将会对密度分层产生影响。为了控制变量，海水温度变化也仅仅体现在密度项中，参考温度TRef依然取常数。需要补充说明的是，式（4）描述了温度与密度的关系，在此基础上可以得出单位体积海水所受的重力为：

所受浮力为：

式（6）与式（5）相减，得到浮力与重力的合力大小为：

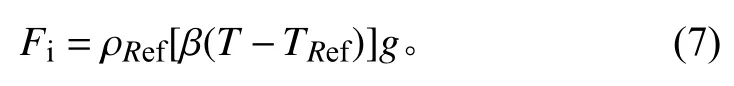
由于数值仿真软件设置的实际需要，参考密度ρRef仍取常数，而其影响完全放在膨胀系数 β 中考虑。为了使浮力与重力的合力保持不变，定常膨胀系数β变为 β′，两者关系如下：

其中： ρRef为常数； ρ (h)为密度分层在深度h方向上的变化情况。

2 CFD模拟

2.1 计算区域与边界条件

2.1.1 计算区域

数值仿真的计算区域如图2所示，整个计算区域x方向（航行方向）长为120 m，z方向宽为80 m，y方向（垂直方向）高为70 m。喷嘴（即热射流出口）离顶端自由液面高度为50 m，距离入口平面长度为5 m。整个计算区域划分为1，2，3三个区域。根据计算精度的需要，分别对这3个计算区域划分了疏密不同的网格，其中，喷嘴位于计算区域1中，其网格质量将会影响整个热射流流场的分布，因此对该区域的网格进行了加密处理，尤其在喷嘴周围使用了高密度的O型网格。

图2 计算区域Fig.2 Computational region

2.1.2 边界条件

计算区域左侧面设置为入口边界条件，入口海水温度为15℃；喷嘴也设置为入口边界条件，热射流的速度大小为0.33m/s。右侧面设置为出口边界条件，其余外侧面均为自由滑移壁面。计算区域内部的接触面设置为interfaces。

2.2 工况计算

图1定量描绘了40° N海域，50 m水深海水密度的典型分布，不难发现其变化范围极小。因此，定义海水的密度分层值φ为：50 m深度海水密度 ρ50与表面海水密度 ρ0的差值 (ρ50-ρ0)，与表面海水密度 ρ0的比值（表面海水密度 ρ0为定常数），即

图3给出了相同时刻，密度不分层φ=0%与密度分层值φ=1%的温度云图对比，可以看出两者几乎没有差别。这说明，φ 值较小的密度分层对热射流流场的影响并不明显。

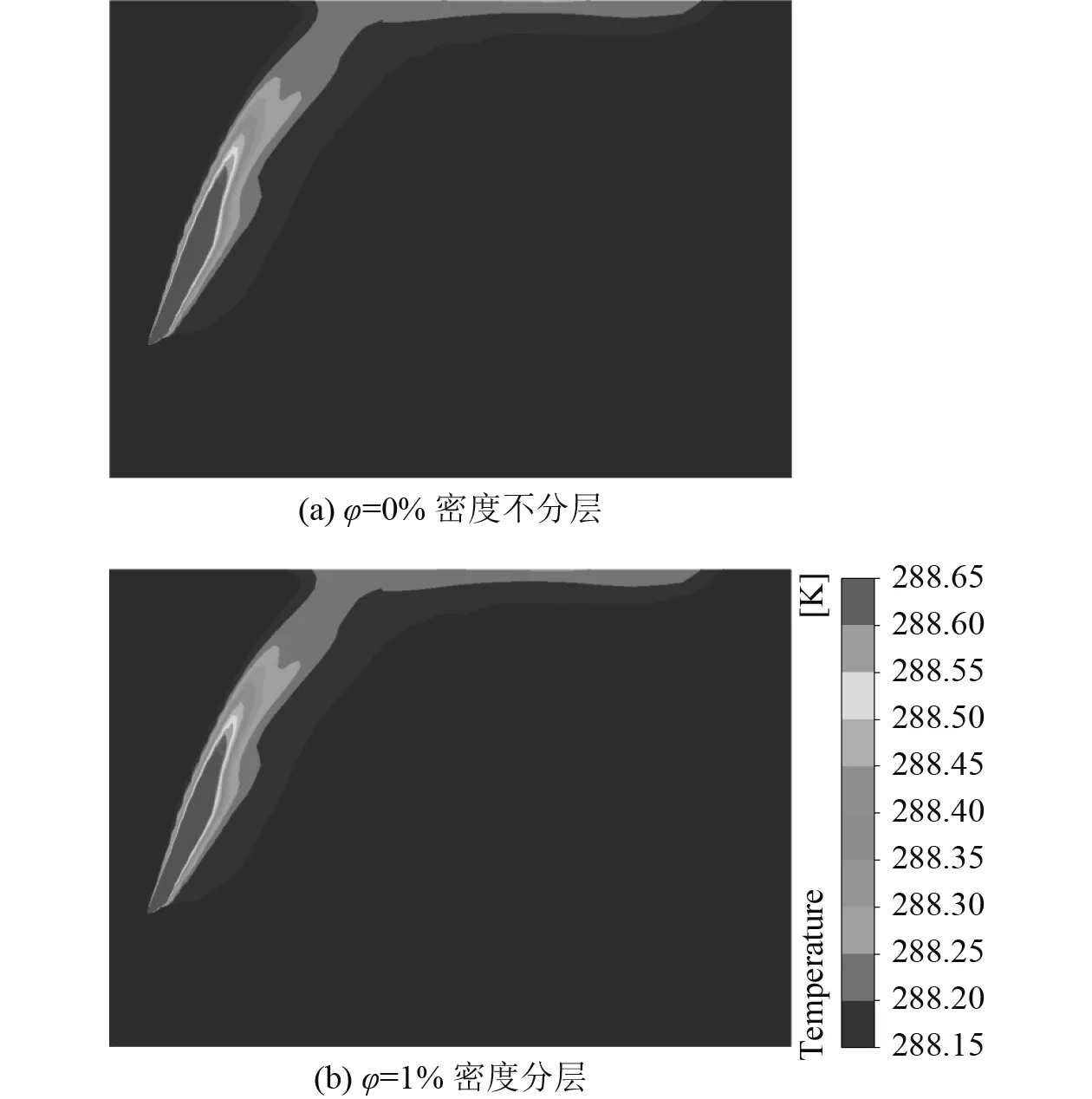
图3 t=16min，xy截面温度云图Fig.3 xy section temperature nephogram in 16 min

为了在数值计算结果中体现密度分层对热射流的影响，需使密度分层的影响远大于数值计算误差，因此数值仿真计算选取水下航行体航速V为0 kn，0.1 kn，0.2 kn，密度分层值φ为0%，50%，100%，热射流与海水的温差 ΔT为30℃，40℃，50℃。显然数值仿真中φ值50%，100%的计算结果并不能直接应用于实际环境，为了解决φ值偏小无法体现密度分层影响以及φ值偏大与实际不符的问题，将对仿真结果进行曲线拟合，得出任意φ 值情况下，密度分层对热射流流场的影响规律。

3 密度分层对热射流影响的仿真分析

3.1 密度分层影响的定性说明

采用热射流高度H作为衡量热射流影响的指标，假设海水温度为15℃，若受热射流影响使温度上升0.01℃，图4给出了热射流某时刻温度15.01℃的等值面图，任意时刻热射流高度H定义为此时喷嘴中心到T=15.01℃温度等值面顶端的垂直距离。

图4 15.01℃等值面Fig.4 15.01 °C isosurface

密度不分层情况下，随着航速增加，相同时刻热射流的高度H逐渐降低；随着热射流温度的提高，相同时刻热射流的高度H逐渐升高。图5与图6对比了相同密度分层值=50%情况下，水下航行体航速、热射流温度对热射流流场的影响，结果表明上述规律依然成立。由图5可知，在热射流出口温度为45℃情况下，航速0.2 kn相对于航速0.1 kn，其热射流15.01℃等值面顶端较低，即热射流高度H较低；由图6可知，在航速0.1 kn情况下，热射流出口温度55℃相较于出口温度45℃，其热射流高度H较高。

图5 t=4 min，热射流15.01℃等值面Fig.5 Hot jet 15.01 °C isosurface at 4 min

图6 t=4 min，热射流15.01℃等值面Fig.6 Hot jet 15.01 °C isosurface at 4 min

由φ的定义可知，φ值越大，则某一固定深度处的海水密度ρRef越大。式说明此时热射流所受浮力与重力的合力Fi也越大。因此φ值越大，热射流漂浮的速度越快，相同时刻热射流的高度H也越高。

3.2 密度分层影响的修正

为了体现密度分层影响对热射流流场的影响，引入密度分层影响的修正系数 ω ，定义式如下：

其中：H0为密度不分层（即φ =0），某一确定的时间t、航速V、温差 ΔT工况下的热射流高度；Hφ为密度分层值φ时，相同时间t、航速V、温差 ΔT工况的热射流高度。若是能够得出修正系数 ω ，则任意密度分层值φ时的热射流高度为：

图7（a）列出了 ΔT=30◦C ，V=0.1 kn，不同φ值的热射流高度曲线；图7（b）列出了 ΔT=30◦C，V=0.2 kn，不同φ 值的热射流高度曲线。通过图7发现，在温差ΔT、航速V相同时，随着密度分层值φ的增加，热射流的漂浮速度是逐渐增加的，即相同时间t热射流高度Hφ增大。密度分层值φ表征了相同深度海水的密度大小，φ 值越大，表征海水密度越大；而热射流所受浮力大小Fi与海水密度正相关，即相同时刻热射流的高度Hφ更大。

图7 ΔT=30◦C ，不同φ 值的热射流高度曲线Fig.7 At ΔT=30◦C, Heat jet height curves with differentφ values

图8列出了 ΔT=30◦C，φ =50%，不同航速V的热射流高度曲线。由图8可知，在密度分层φ =50%情况下，随着水下航行体航速V由0增加到0.2 kn，热射流相对于周围海水的速度变大，两者的对流换热更加剧烈，导致热射流受到的浮力变小，热射流高度Hφ逐渐降低

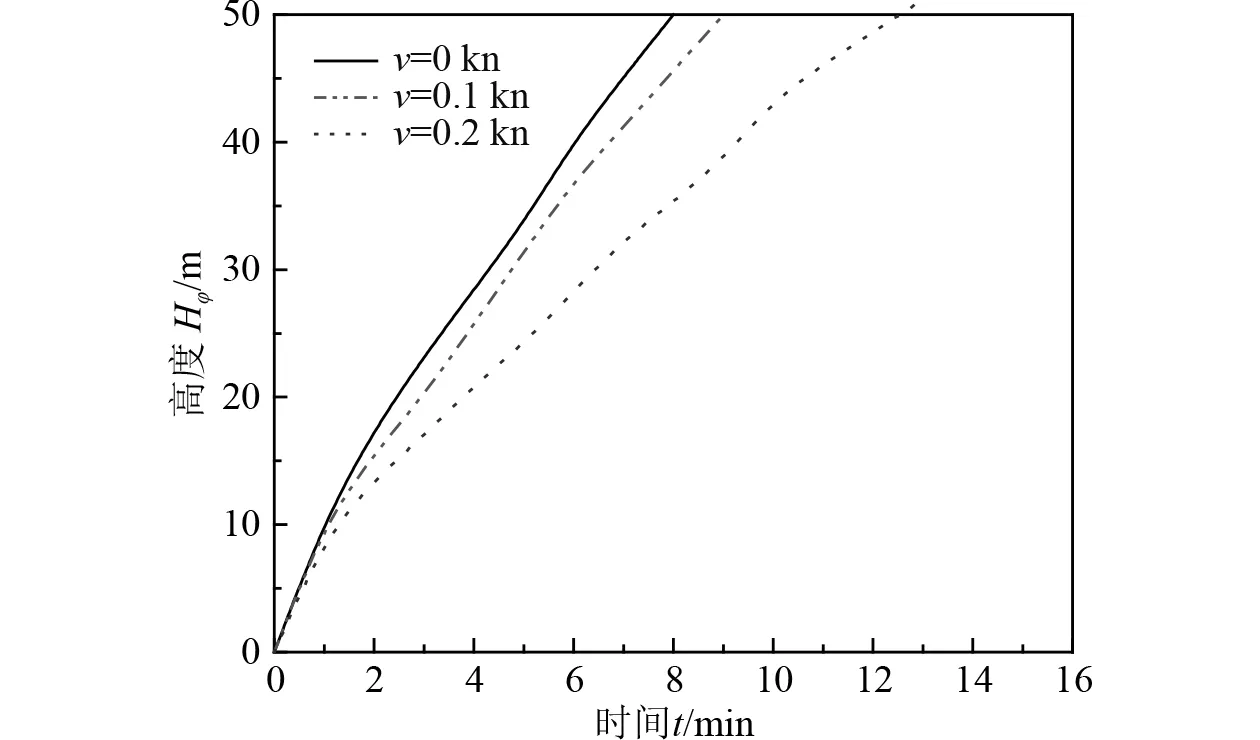
图8 ΔT=30◦C ，φ =50%，不同航速V的热射流高度曲线Fig.8 At ΔT=30◦C andφ =50%, Hot jet height curves with different speedV

图9列出了V=0.1 kn，φ =50%，不同温差 ΔT热射流高度曲线。由图9可知，在密度分层φ =50%情况下，随着温差 ΔT由30℃上升到50℃，热射流在与周围海水混合过程中温度较高，其上浮过程中受到的浮力增大，热射流高度Hφ逐渐升高。

图9 V=0.1 kn，φ =50%，不同温差 ΔT热射流高度曲线Fig.9 AtV=0.1 kn andφ =50%, Hot jet height curve with different temperature difference ΔT

图10～图14分别列出了改变密度分层值φ 、航速V或温差 ΔT其中一个变量时，密度分层修正系数ω与时间t的关系曲线，不难发现图中各密度分层修正系数ω均是随着时间t的增加而下降的。图10～图12显示在温差 ΔT与航速V固定时，随着密度分层值φ的增大，密度分层修正系数ω曲线向上移动，这是由于分层值φ 的增加，使得热射流所受浮力增大，相同时间内热射流高度Hφ越大，相应的密度分层修正系数ω值越大。从图13可以看出，随着航速V的增大，密度分层修正系数ω曲线向上移动。由于在密度不分层情况下，航速V的增大使得热射流高度H0减小，根据定义式(10)有 ω =Hφ/H0，因此在航速V较大情况下，H0较小使得密度分层的影响更加突出，密度分层修正系数ω曲线上移。从图14可以看出，随着温差 ΔT的提高，在密度不分层情况下，热射流高度H0是逐渐增大的，使得密度分层的影响减小，密度分层修正系数ω曲线下移。

图10 ΔT=30◦C ，V=0.1 kn，不同φ 值的密度分层修正系数ω曲线Fig.10 At ΔT=30◦C andV=0.1 kn, Density stratificationcorrection coefficientω curves with differentφ values

图11 ΔT=30◦C ，V=0.2 kn，不同φ 值的密度分层修正系数ω曲线Fig.11 At ΔT=30◦C andV=0.2 kn, Density stratificationcorrection coefficientω curves with differentφ values

图12 ΔT=40◦C ，V=0.1 kn，不同φ 值的密度分层修正系数ω曲线Fig.12 At ΔT=40◦C andV=0.1 kn, Density stratification correction coefficientω curves with differentφ values

图13 ΔT=30◦C ，φ =50%，不同航速V下密度分层修正系数ω曲线Fig.13 At ΔT=30◦C andφ =50%, Density stratification correction coefficientω curves with different speedsV

图14 V=0.1 kn，φ =50%，不同温差 ΔT下密度分层修正系数ω曲线Fig.14 AtV=0.1kn andφ ==50%, Density stratification correction coefficientω curves with different temperature differenceΔT

由图10～图14可知，密度分层值φ 、航速V、温差ΔT以及时间t均会影响密度修正系数 ω。假设 ω关系式如下：

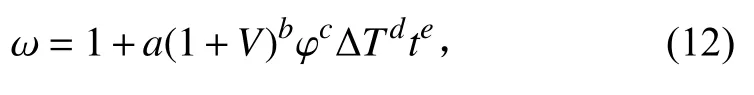
当φ =0时，热射流高度不需要修正，即 ω =1，因此关联式中第一项为常数1；其次，第二项设置成指数函数的原因在于，随着密度分层值φ 、航速V（kn）、温差 ΔT（℃）以及时间t（min）的变化，密度修正系数 ω 均是呈现单调变化规律的，这与指数型函数相符；显然当航速V=0 kn，密度分层值φ ≠0时，热射流高度依然需要修正，即 ω ≠1。若航速影响项为Vb，则有 ω =1，因此指数函数项出现了 (1 +V)b。 ΔT=0表征热射流与周围环境不存在温差，不会上浮；t=0表征热射流还没有排入海水中，因此温差与时间两项直接写成指数的形式即可。通过Matlab对数值仿真中8个工况，共66个数据点进行拟合，得出密度修正系数 ω 拟合式如下：

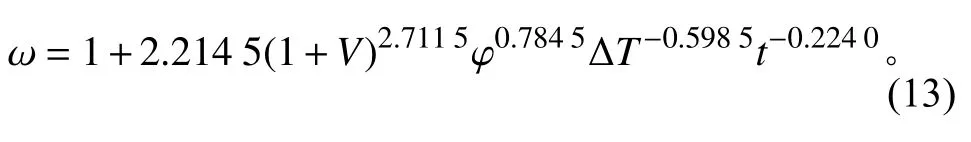
该式的验证范围是：0 kn≤V≤ 0.2 kn，0≤ φ ≤100%，30℃≤ ΔT≤50℃，1 min≤ t≤ 12 min。

该拟合关联式的计算结果与数值仿真结果对比，误差在6%以内，且绝大部分数据点的误差都在1%以下。因此在确定密度分层值φ 、航速V、温差 ΔT以及时间t的情况下，可以方便准确地通过式(13)求得密度修正系数 ω 。再利用式(11)即可求得对应的密度分层值φ 、航速V、温差 ΔT以及时间t下，热射流的高度Hφ。

4 结 语

水下航行体航行过程中，其动力系统的废热以冷却水的形式向外界直接排出，在密度差的作用下向海面浮升。实际海洋环境下，海水密度随水深是变化的，而热射流浮升力的大小受海水密度的影响。基于此，本文研究了密度分层对热射流流场的影响，结论如下：

1）随着海水深度的增加，海水的盐度上升，温度下降，这两者均会造成海水密度随深度的增加而增大；

2）所得到的拟合关联式计算结果与数值仿真结果对比，误差在6%以内，且绝大部分数据点的误差都在1%以下。