基于无人机航拍图像快速拼接方法的研究

赵丽颖，付强，黄丹飞，钟艾琦，张玉爽

（长春理工大学 光电工程学院，长春 130022）

无人机具有操作简单、反应速度快、飞行灵敏、成本低、携带方便等特点，已被广泛应用于抗震救灾、防汛、军事侦察、海上勘测、交通监管等区域。而无人机上设备在拍摄图像时，由于成像设备性能和飞行高度等因素的限制，一般情况下，获取的单幅图像能够覆盖的地面景物范围较小，很难覆盖整个要拍摄的区域。为了对拍摄目标区域信息有更好的掌握，快速得到更多的目标区域有效信息，无人机航拍图像快速拼接已成为迫切需要。

目前无人机的航拍图像拼接方法主要是以基于图像特征的拼接方法为主，基于图像特征拼接方法中，图像配准与图像融合是图像拼接最重要的两个关键步骤。图像配准是无人机影像拼接过程中的核心步骤，配准精度直接影响图像拼接的质量。在基于特征图像拼接的算法中，目前提取图像特征点的算法有SIFT[1]（Scale-Invariant Feature Transform，尺度不变特征变换）算 法、Harris角点算法、SURF（Speed Up Robust Feature）等算法。Harris C[2]提出了 Harris角点检测算子，该算法对角点响应函数进行阈值判断处理，并提取局部最大值来进行角点的提取，但是该算法检测特征的速度慢且不具备尺度不变性。SIFT特征匹配算法是一种比较经典的算法，它通过在空间尺度中寻找极值点，并提取出其位置、尺度、旋转不变量等特征，提取出的特征比较稳定，数量多、计算量大、耗时长。Bauer[3]提出了一种SURF算法，SURF算法利用海森矩阵确定特征点然后进行非极大抑制，它降低了计算难度，并且提高了特征检测速度。赵文君等人[4]利用提取特征点区域限制的方法限制Harris角点生成的面积，再结合非极大值抑制算法剔除粗差和聚簇角点，利用最佳缝合线融合方法进行图像融合，得到了良好的拼接效果。文伟东等人[5]提出基于SIFT算法对有序图像拼接算法，首先对图像的顺序进行排列，然后利用FAST算法进行特征提取，并对随机一致性算法进行改进删除误匹配点对，最后运用加权平均融合算法进行融合。陈雪涛等人[6]提出一种基于SURF算法和重叠区域相结合的视频拼接算法，视频拼接效果能够很好地消除鬼影等问题。管增伦[7]利用改进的SURF算法针对视频图像重叠区域进行特征点提取，提高算法运行速率，实时性高，拼接效果好。程德强[8]采用SURF特征算法提取特征点，然后利用改进的随机抽样一致算法删除误匹配点。对于重叠区域进行动态融合处理，从而消除视频重叠区域的拼接缝和鬼影。年华[9]将Harris-Laplace算法检测与SURF算法相结合的拼接方法，运用RANSAC算法剔除错误匹配点，提高了匹配效率。马嘉林[10]提出了一种基于相机标定的全景图拼接方法，对图像进行几何畸变校正处理，在利用图像的同名点实现图像的配准并完成拼接。李玉峰[11]提出了一种基于区域分块与SIFT算法相结合的图像拼接的算法，利用NCC算法分割出匹配图像与待匹配图像间的相似区域，利用SIFT算法进行特征提取，实现图像之间的无缝拼接。文献[12]对待拼接的图像先进行柱面投影，然后利用SIFT算法进行特征点提取，利用RANSAC方法删除误匹配完成图像配准。

针对基于特征点拼接速度较慢且不能进行地理定位问题，提出了一种基于无人机POS系统数据图像拼接的方法。首先对POS数据的精度较低问题，建立航拍参数的优化模型提高数据精度，利用优化后的POS数据计算出影像四角点的地理坐标，将第一张图像地理坐标作为基准，进行航拍有序影像的拼接。

1 基本原理

1.1 无人机POS系统简介

POS（Position and Orientation System）是 DGPS/IMU组合定位定向系统的统称。它既有差分GPS实时定位的功能，又具备IMU测定姿态的能力，把其搭载在无人机平台上就能测定动态目标的三维坐标和航摄仪三个轴线上的角度信息。POS最大的优点是取长补短，它把具备定向功能的陀螺仪和具备定位功能的GPS有力地结合在一起，然后把数据处理技术—卡尔曼滤波技术引入IMU与GPS的组合系统之中，使此组合系统的稳定性、定位定向精度和自动化程度有了大幅度的提高，GPS与IMU的组合系统拥有“黄金搭档”之称[13]。

1.2 基于POS数据优化模型

由于无人机航拍过程当中会受到地理位置、环境、风速以及无人机POS数据自身的测量误差等影响，得到的定位信息有所误差。为了能够更好地提高无人机POS数据的精度，利用光束法区域网平差来建立优化方程。如图1所示，光束区域网平差是以一张像片组成的一束光线作为平差的基本单元，以中心投影的共线方程作为平差的数学模型。以相邻像片公共交会点坐标相等、控制点的内业坐标与已知的外业坐标相等作为平差条件，列出控制点和加密点的误差方程式，进行全区域的统一的平差计算，求解出每张像片的外方位元素和加密点的地面坐标。

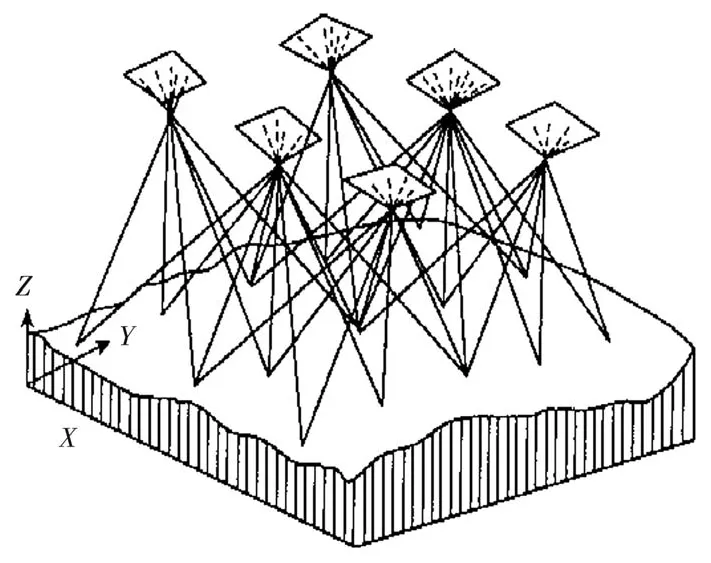
图1 光束区域网平差

利用光束区域网平差通过设置控制点获得外方位元素与无人机POS系统的初始的外方位元素建立优化参数方程。POS系统数据优化流程图如图2所示。

图2 POS系统数据优化流程图

优化方程：

根据公式（1）—公式（6）可以得到校正后的参数，然后利用校正参数对原始POS数据进行优化。其中 ΔXp，ΔYp，ΔZp，Δψp，Δθp，Δφp为校正后得到的结果；XP1，YP1，Zp1，ψp1，θp1，φp1为图像初始的外方位元素与姿态参数；Xpn，Ypn，Zpn，ψpn，θpn，φpn为第n个图像的初始外方位元素与姿态参数；n为计算中涉及的图像数量。表1为无人机POS数据。

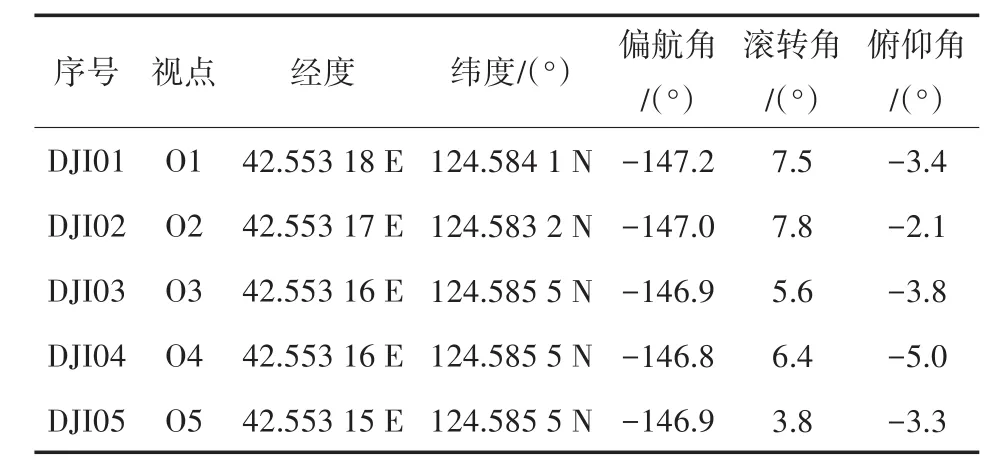
表1 无人机POS定向数据

图3和图4分别为初始数据与优化后的数据。从优化后的数据图可以看出偏航角的数据前后变化不大，而滚转角与俯仰角经过优化后数据连续，能够更好地进行地理定位。

图3 初始数据

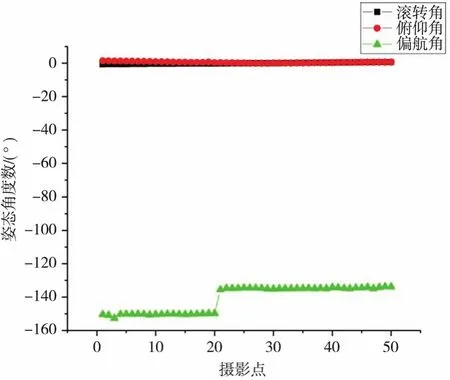
图4 优化后数据

1.3 基于POS系统数据无人机图像拼接

为了能够快速获得航拍图像的有效信息，并能够更好地精确定位，采用优化后的POS系统数据进行图像拼接。

1.3.1 坐标变换

（1）像平面坐标系到像空间坐标系的转换

像平面坐标系通常将图像的左上角设为坐标原点，而像空间坐标系是将图像中心设为原点。两个坐标系坐标的关系为：

式中，(u0×s，v0×s，-f)为图像平面坐标系坐标，s:x轴，y轴每个像素的物理尺寸；u0为图像像素高度的一半，v0为图像像素宽度的一半；f为相机焦距。

（2）像空间坐标系到像空间辅助坐标系转换

假设已知像点a，它在像空间辅助坐标系中的坐标可表示为(X,Y,Z)，在像空间坐标系中的坐标为(x,y,-f)，两个坐标系坐标关系为：

式中，a1，b1，c1为方向余弦，即两个坐标轴之间的余弦值。由外方位元素（偏航角φ，俯仰角θ，横滚角φ）计算得到。R为旋转矩阵，可以由下面3个旋转矩阵式求得：

（3）像空间辅助坐标系到地面坐标系转换

设摄影中心S与地面点A在地面摄影测量坐标系D-XtpYtpZtp中的坐标分别为Xs,Ys,Zs（即像片外方位直线元素）和XA,YA,ZA，则地面点A在像空间辅助坐标系中的坐标可表示为XA-XS，YA-YS，ZA-ZS，而对应点a在像空间辅助坐标系中的坐标可表示为X，Y，Z。已知S，a，A三点共线，利用相似三角形关系可以得到：

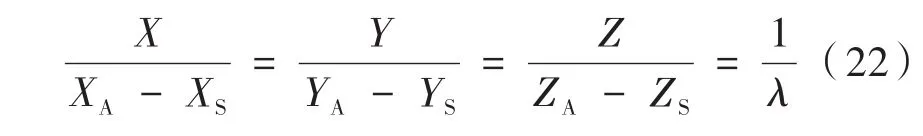
式（22）中λ为比例因子，写成矩阵形式为：

利用像点的像空间坐标与像空间辅助坐标关系式可得其逆变换公式为：

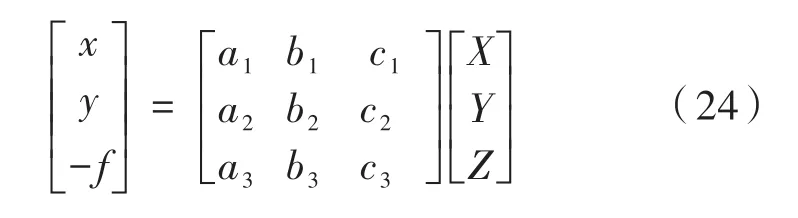
将式（22）代入式（24），并用第三式去除第一，二式得：

式（25）就是中心投影构想的基本单位，即共线方程。

1.3.2 确定图像四角点坐标

已知相机参数f，x0，y0（f为相机焦距，(x0,y0)为像主点坐标），像素大小为s。可以确定图像的四个角点在像空间坐标系的坐标分别为：

其中，w为原图像的宽度；h为原图像的高度。使用上面的公式可以计算地面坐标系中四个顶点的坐标。XA，YA为角点真实坐标，ZA对应为地面点实际高度，使用测量中的平均高度进行计算。

Xmax，Xmin，Ymax，Ymin可由四个地面坐标系的四个角点来确定。利用无人机空间分辨率可以计算出校正后图像的宽度与高度。

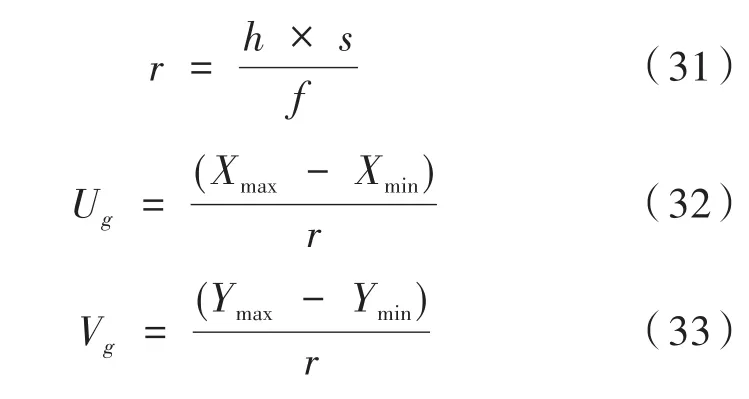
其中，r为无人机空间分辨率；h为相对高度；s为像素大小；Ug，Vg分别为校正后的高度和宽度。

1.3.3 经纬度转换大地坐标系

由于试验POS数据中摄影瞬间摄影中心的平面坐标是经纬度，所以需要利用高斯投影坐标公式求取摄影中心的实际坐标。

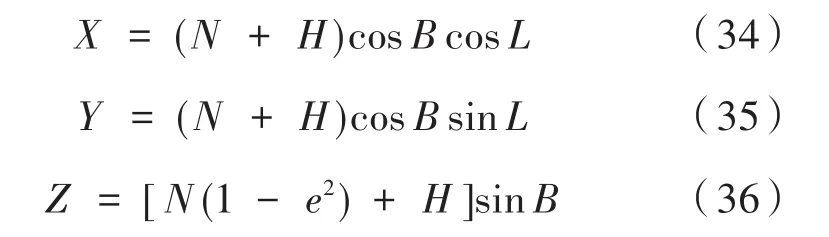
其中，（B，L，H）为大地坐标，B，L，H分别表示POS数据中的纬度、经度和高程；（X，Y，Z）为空间直角坐标；N为卯酉圈曲率半径；e为椭球第一偏心率。

1.4 基于SURF算法图像拼接

SURF（Speed Up Robust Features）算 法[14]是一种尺度和旋转不变的检测与描述算法。SURF算法是SIFT算法的一种改进。它和SIFT算法的特点一样具有很强的鲁棒性，对图像的亮度、尺度、角度旋转、噪声等具有不变特性，它的运算速度比SIFT算法更快。SURF算法计算步骤如下：

（1）构造Hessian矩阵

SURF算法与SIFT有很大的不同。SIFT算法采用的是DOG图像，而SURF算法采用的是Hessian矩阵行列式近似值图像。假设函数f( )x,y，Hessian矩阵H是由函数和偏导数组成。首先计算图像中某个像素点的Hessian矩阵：

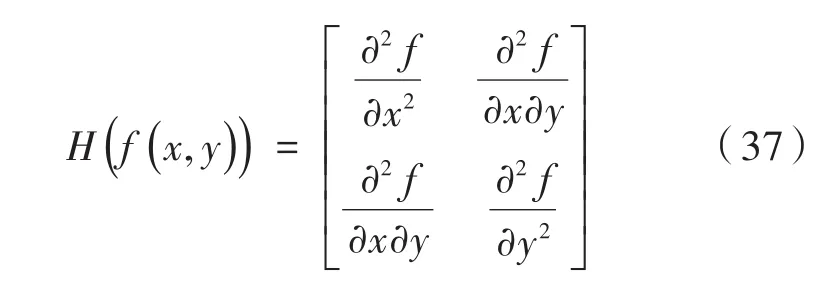
当Hessian矩阵的判别式取得局部极大值时，判定当前点是比周围邻域内其他点更亮或者更暗的点，由此来定位关键点的位置，因此Hessian矩阵的判别式为：

在离散空间上，为了得到Hessian矩阵的四个元素，SURF采用二阶标准高斯函数对图像进行卷积运算，高斯函数可构造出不同尺度下的响应函数图像。在尺度σ下，对应的Hessian矩阵：

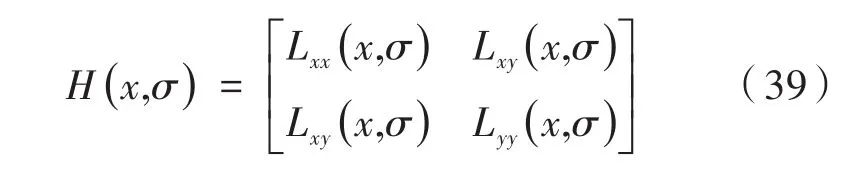
Lxx(x,σ),Lxy(x,σ),Lyy(x,σ) 为点x处高斯函数的二阶偏导数与图像I的卷积。计算出图像上所有点的Hessian行列式值：

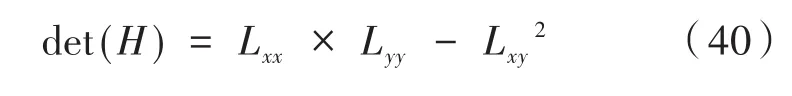
用行列式的值来判别图像局部特征点。如图5所示分别为盒式滤波器和高斯滤波器示意图。为了提高运算速度，SUFR算法使用盒式滤波器来代替高斯滤波器，因此添加了加权系数0.9。则H矩阵判别式可表示为：

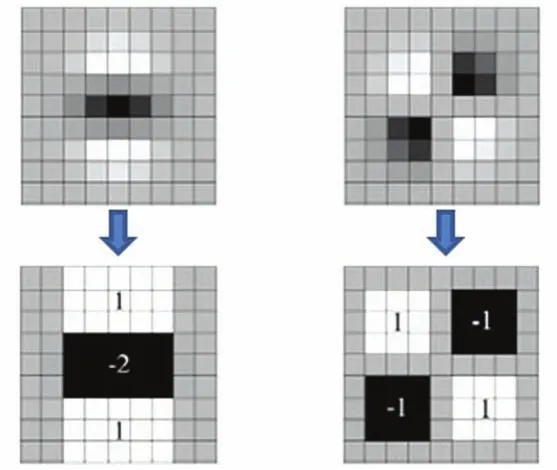
图5 盒式滤波器和高斯滤波器示意图

（2）构造尺度空间

SURF算法的尺度空间由O层和S层组成，区别在于，SIFT算法下一组图像的长宽均是上一层的12，同一组不同层图像之间的尺寸是一样的，但是所使用的尺度空间因子σ逐渐增大；而在SURF算法中，不同组之间的图像尺寸都是一致的，不同组间使用的盒式滤波器的模板尺寸逐渐增大，同一组不同层图像使用相同尺寸的滤波器，但滤波器的尺度因子σ逐渐增大。如图6所示为尺度空间示意图。

图6 尺度空间示意图

（3）特征点精确定位

经过Hessian矩阵处理过的每一个像素点与其3维领域的26个点进行比较大小，如果该点是26个点中的最大值或者最小值，则保留下来，当做候选特征点，否则会删除该点。图7表示为特征点定位过程。

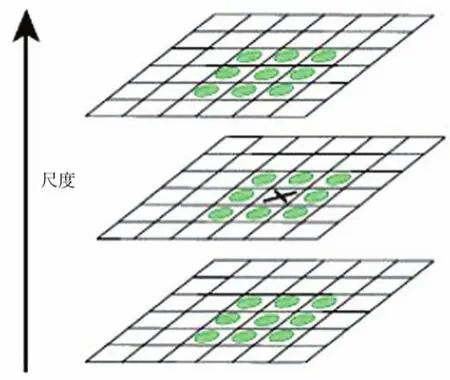
图7 特征点定位

（4）特征点主方向

SURF算法中特征点主方向计算采用的是统计特征点圆形邻域内的Harr小波特征，统计60度扇形内所有点的水平、垂直Harr小波特征总和，然后扇形以0.2弧度大小的间端进行旋转并再次统计该区域内Harr小波特征值，最后将最大值的那个扇形的方向作为该特征点的主方向，该过程如图8所示。

图8 特征点方向

（5）生成特征描述

为了保证特征矢量的旋转不变性，在SURF算法中，在特征点周围取正方形框，把该框分为16个子区域，每个子区域统计25个像素的水平方向和垂直方向的Harr小波特征，这样每个小区域就有4个值，所以每个特征点就是16×4=64维的向量。图9为特征描述符的构成示意图。

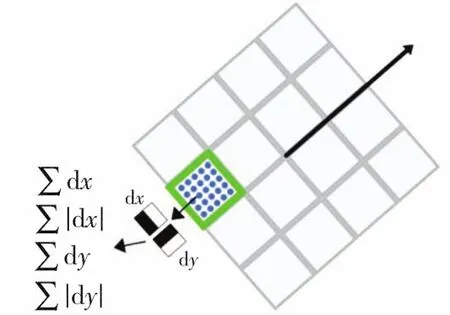
图9 特征描述符的构成

2 实验结果与分析

实验数据由大疆精灵3无人机拍摄得到。仿真实验软件为Matlab R2018b。无人机主要性能指标如表2所示。无人机的航行速度，飞行时航拍高度，曝光点的飞行经纬度信息以及姿态参数等，都可以通过无人机携带的POS系统获取到。设置横向重叠率为75%，旁向重叠率为35%。试验结果如图10、图11所示。

表2 无人机性能指标

图11 不同场景、不同图像数量基于POS数据算法拼接结果

表3是基于SURF特征图像拼接算法与基于POS数据拼接算法进行对比。从结果上来看算法在图像数量分别为12张、30张、50张比基于SURF特征图像拼接算法在速度上分别提高了40%、34%、30%，能够直接对目标区域进行地理定位。

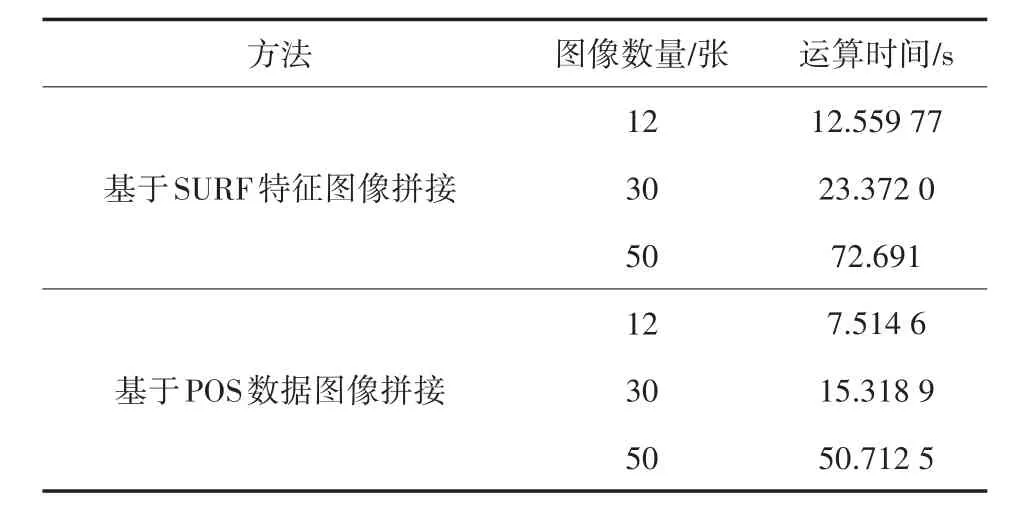
表3 基于SURF特征图像拼接算法与基于POS数据拼接算法运算时间的比较

3 图像质量评价

图像质量的好坏可以通过图像质量评价来进行评判。图像质量评价可分为主观评价与客观评价。主观评价通过人眼进行观察，属于偏主观的一个概念。但主观评价结果较难准确量化并耗时过长。因此需要进行图像客观评价分析。客观图像质量评价方法主要有峰值信噪比PSNR和基于结构相似度SSIM。下面对拼接后的结果进行主观评价与客观评价分析。

表4列出对拼接结果的主观评价与客观评价。从主观评价上来看基于SURF特征算法与基于POS数据拼接结果整体效果良好，但在某些部分还是存在一些重影和边缘缺失。从客观评价整体上来看基于SURF算法的图像失真度比基于POS信息拼接结果图像失真度大。

表4 图像质量评价分析

4 结论

提出一种基于无人机航拍图像快速拼接的方法。首先对无人机POS系统的数据进行优化引入光束区域网平差方法并建立优化方程，然后利用POS数据计算出影像四角点的地理坐标，以第一张影像地理坐标为基础，进行航拍有序影像的拼接。最后得出结果与基于特征点图像拼接的方法进行对比，基于POS数据算法的拼接方法效率更高。对于拼接图像像质评价采用主观评价与客观评价的方法，结果显示基于POS数据拼接结果效果良好。但基于POS数据拼接还有很多不足之处，当POS数据精度较低时结果会出现拼接错误或部分数据缺失，因此对于优化数据模型还需要进一步优化。接下来的主要工作是得到更多的数据来进行优化。