一类基于SDIR模型的PM2.5预测研究模型及应用

高庆玲，徐 东，杨晓芳

(成都师范学院数学学院，成都 611130)

PM2.5又称细颗粒物，是环境空气中空气动力学当量直径≤2.5 μm的颗粒物，PM2.5在空气中含量浓度越高表示空气污染越严重。虽然PM2.5是地球大气成分中含量很少的组分，但却不能忽视。PM2.5具有直径小、接触面积大、活性强、容易吸附带有有毒有害物质、在大气中滞留时间长输送距离远的特点，对人体健康和大气环境质量影响很大。

许多学者对大气污染进行了深入研究，除PM2.5外，空气质量AQI的基本监测指标分别为可吸入颗粒物PM10、一氧化碳CO、二氧化硫SO2、二氧化氮NO2及臭氧O3。大量研究表明，空气质量监测指标中的PM10、CO、SO2、NO2、O3和PM2.5之间有着很大的联系，选取这6项基本监测指标作为本研究的变量，分析成都市PM2.5和其他空气污染物之间的动态关系，希望能够有效控制PM2.5。研究数据来源于成都空气质量指数AQI-PM2.5月统计历史数据-中国空气质量在线监测分析平台历史数据[1]。

1 研究方法与数据模型

利用互联网查得成都市2020年空气质量环境监测数据，基于SDIR模型，运用相关性分析法与多元回归法，根据数据，分析PM2.5与各个指标之间的相关性，利用相关系数分析各指标的独立性[2]，由此建立PM2.5多元线性回归方程，借助MATLAB软件对PM2.5进行多元线性回归方程拟合，并对模型进行检验，得到PM2.5与其他5项指标之间的关系表达式，分析PM2.5与其他影响因素的动态关系。

1.1 多元线性回归分析

采用Pearson相关系数建立任意两个监测指标之间的联系。Pearson简单相关数计算式：

其中，r为相关系数，xi、yi分别为随机变量x与随机变量y的第i个样本值，样本容量为n。相关系数r的取值范围为[-1,1]，相关系数的绝对值越大，相关性越强，即相关系数越接近于1或-1，相关性越强，相关系数越接近于0，相关度越弱，其中：

若0r>0,表明x与y之间存在负相关关系；当|r|=1时，表明其中一个变量的取值完全取决于另一个变量；当r=0时，表明x与y之间不相关。

通过相关系数计算检验结果，建立各监测指标间的多元线性回归模型。利用MATLAB软件计算Pearson相关系数。结果发现，PM2.5与其他各指标之间均存在不同程度的相关性，PM2.5与PM10的Pearson相关系数为0.941 3，与CO的为0.606 6，与SO2的为0.775 7，与NO2的为0.572 0，与O3的为-0.632 1。

通过分析可知，PM2.5与PM10、SO2、NO2、CO存在显著正相关，与O3存在负相关。故将PM2.5作为因变量，其他5项指标作为自变量，从而研究PM2.5与其他5项分指标之间的相关性并对其关系进行分析。多元线性回归模型是用来进行回归分析的数学模型，可以使相关变量中的一个因变量与多个自变量之间建立线性关系，通过最小二乘参数估计方法减小误差得到各个回归系数，定量研究各变量之间的线性关系[3]。

设：PM10为x1，CO为x2，SO2为x3，NO2为x4，O3为x5，PM2.5为y，权重系数为β1，β2，…，β5，误差项为μ。

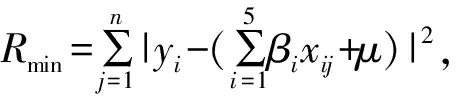
1.2 结果分析

通过搜集数据、以误差最小为约束条件，利用MATLAB，分析计算多元回归方程，经过调整修正得到回归系数β1，β2，β3，β4，β5，μ的估计值分别为0.621 3，-0.847 5，55.542 1，-0.009 5，0.015 4，-35,273 0；回归系数的置信区间分别为[0.447 8,0.794 8][-2.294 2,0.599 3][38.631 9,72.452 2][-0.479 5,0.460 6][-0.029 0,0.059 8][-56.822 0,-13.724 0]，拟合度为R2=0.996 9，F统计量为F=317.112 6。由此得到回归方程式：

y=0.621 3x1-0.847 5x2+55.542 1x3-0.009 5x4+0.015 4x5-35.273 0

因其拟合优度为R2=0.996 9，说明拟合效果很好，PM2.5与其余5项之间具有很好的线性关系。综上可知，在空气质量指数监测指标中，PM2.5与CO相关性很高。

2 基于SDIR模型对PM2.5探究

2.1 建立模型

经典的SIR模型将节点状态假设为：易感染状态(susceptible，S)、感染状态(infected，I)、免疫状态(recovered，R)。根据SDIR网络传播模型[4]，针对各因素对PM2.5的影响建立SDIR模型。

把各因素对PM2.5的影响过程分为未影响状态(susceptible，S)、正在影响状态(infected，I)、暂未影响状态(disguiser，D)、已影响状态(recovered，R)。其中，S点表示未对PM2.5造成影响；I点表示正在对PM2.5造成影响；D点表示已发生变化，但暂未对PM2.5造成影响；R点是已对PM2.5造成影响。由于对PM2.5造成影响的因素多样，会产生许多不一样的情况，因此本研究仅限其中的一种因素的变化、其他条件不变的情况下对其进行研究，据此有下述表达式，表示为各点随时间的变化率。

SDIR模型的表达式为：

2.2 探究温度对PM2.5的影响

令P1为温度发生改变的概率，P2为温度不变的概率，P3、P4、P5为温度继续改变的概率。选取2020年成都市每月平均气温数据[5]，依据SDIR模型，对成都市2020年PM2.5浓度进行分析，结果发现，夏季，由于气温高，PM2.5浓度低；冬季，由于气温较低，PM2.5浓度高，因此PM2.5浓度随着温度的改变而改变，温度越高，PM2.5浓度越低。

3 结论

对空气质量指数的监测指标进行研究，利用相关性分析法、多元线性回归得出PM2.5与PM10、CO、NO2、SO2、O3相关性很高。建立SDIR模型，得出温度会在一定程度上影响PM2.5浓度，PM2.5浓度随温度的变化而变化，温度越高，PM2.5浓度越低。每到冬季时，由于气温低，导致冬季的PM2.5浓度升高，造成了严重的大气污染，为SDIR模型在环境领域中的应用提供了一定的参考。