不同裂纹故障下锥齿轮行波共振瞬态动力学特性研究*

王添翼，栾孝驰，马胤章，高宇涵，徐 石

（1.沈阳航空航天大学 创新创业学院，辽宁 沈阳110136；2.沈阳航空航天大学 航空发动机学院，辽宁 沈阳110136）

航空发动机中心传动锥齿轮是发动机附件传动系统中重要的部件之一，如果齿轮产生裂纹故障会直接影响发动机正常工作和寿命，甚至引发事故。由于锥齿轮辐板结构薄，其形状与盘形十分相似，并工作在高速、重载等恶劣条件下，容易发生节径型行波共振，乃至断裂失效，严重危害发动机正常安全运行。目前，含齿根裂纹故障的齿轮在行波共振状态下的动力学响应问题还不清楚。因此，阐明故障齿轮行波共振状态下的动力学响应特性规律具有重要意义。

近些年来，国内外许多学者对故障齿轮动力学特性进行了研究与分析。Zhou等[1]对含裂纹的多自由度模型进行了振动分析。唐增宝等[2]建立了齿轮传动系统的振动数学模型，并利用模态分析法与状态空间法相结合的方法进行了求解。郭伟超[3]研究了锥齿轮的动力学特性。卢艳辉等[4]研究了齿轮传动系统的动力学特性并展开了相应的试验探究。孙嘉陵[5]探究了齿轮失效的形式以及控制措施。韩二中等[6]利用齿轮齿间啮合力的形状函数，计算出了圆锥齿轮的2、3节径行波共振应力响应结果。刘天文[7]通过有限元方法计算出了某型发动机中心传动锥齿轮的固有频率。王大勇[8]获得了航空薄辐板齿轮行波共振频率以及齿轮在共振转速和工作转速下动应力结果。国内外诸多学者探究了齿轮故障形成的原因以及对齿轮动力学特性的影响，但是目前对行波共振状态下的故障齿轮动力学响应特性研究鲜有报道。

本文主要研究含齿根裂纹故障中心锥齿轮行波共振状态下动力学响应特性。首先，建立含齿根裂纹故障锥齿轮有限元模型；其次，研究含齿根裂纹锥齿轮行波共振状态下动力学响应特性规律，重点关注齿根裂纹尺寸变化对锥齿轮应力分布和固有频率特性的影响。本文的研究成果可为航空发动机中心传动锥齿轮动力学响应特性研究提供参考，具有一定的工程实际意义。

1 中心锥齿轮模态特性分析

1.1 模型建立及网格划分

本文建立的齿轮模型为航空发动机中心锥齿轮，齿轮主要参数如表1所示，啮合齿轮模型如图1所示[9]。

表1 锥齿轮主要尺寸参数

图1 啮合齿轮模型

本文共建立六种不同长度和深度的齿根裂纹模型，设齿宽总长度为L，裂纹起点到轮齿中线距离为H。裂纹长度分别设置为0.1L和0.8L，裂纹深度分别设置为0.1H、0.3H和0.5H，裂纹方向设置为垂直于齿根平面方向；约束设置为在内孔上的固定约束；齿轮基体网格尺寸设置为2mm，轮齿接触面和齿根部分网格进行细化，细化网格尺寸设置为1mm。

1.2 从动锥齿轮模态分析

1.2.1 健康齿轮

经过计算，我们得到了健康齿轮各阶模态振型，如图2所示。由图2分析可知：从动锥齿轮呈现了1节圆、2节径、3节径、4节径、5节径振型，即具有节圆和节径型振动形态。3、4节径行波共振频率仿真结果与试验结果对比如表2所示，仿真计算与试验测试获得的模态频率误差均在4.0%以内，验证了有限元仿真模型的准确性。

表2 模态分析的仿真值与试验结果对比

图2 健康齿轮模态振型

1.2.2 含齿根裂纹故障齿轮

对含齿根裂纹故障齿轮进行模态分析，提取节径型行波共振频率，并计算具有长度为0.1L和0.8L，深度分别为0.1H、0.3H和0.5H齿根裂纹的齿轮与健康齿轮的固有频率之差，研究不同尺寸齿根裂纹对齿轮固有频率的影响，裂纹长度相同、深度不同时齿轮固有频率变化规律如图3所示。

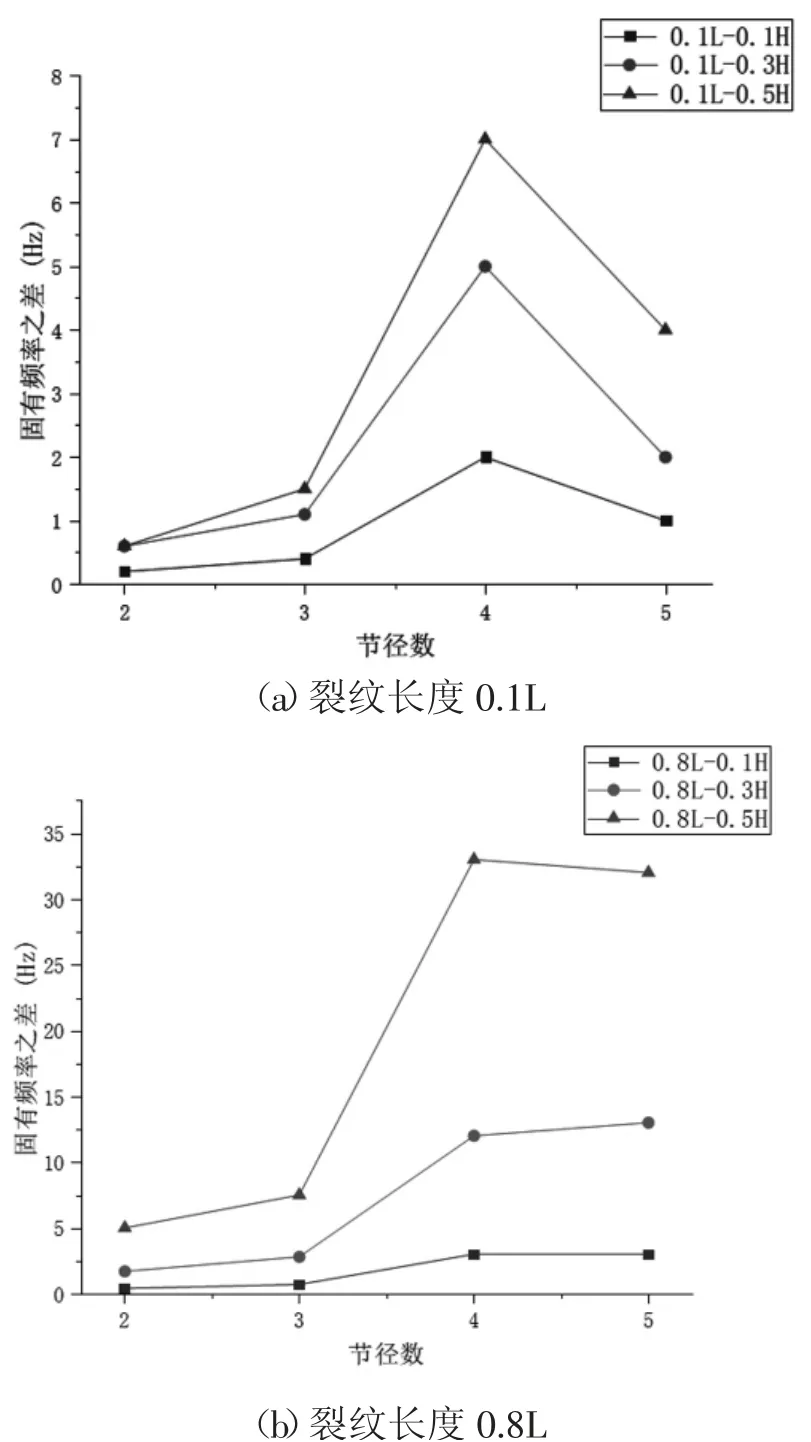
图3 裂纹长度相同、深度不同时齿轮固有频率变化规律

由图3分析可知：齿轮出现齿根裂纹时，齿轮的固有频率呈现下降趋势。当裂纹长度不变，随着裂纹深度的增加，齿轮固有频率差值变大，三种深度的裂纹在2、3节径产生的频率差较小，4、5节径的频率差较大；当裂纹深度不变，随着裂纹长度的增加，齿轮固有频率差值变大，三种深度的裂纹在2、3节径产生的频率差较小，4、5节径的频率差较大；当裂纹长度为0.8L，裂纹深度为0.5H时，4节径产生的频率差值变化最大，达到33Hz。

2 中心锥齿轮瞬态动力学响应特性分析

2.1 齿轮接触与约束设置

基于有限元分析方法和赫兹接触理论对中心传动锥齿轮进行瞬态动力学分析。接触类型为摩擦接触，摩擦系数为0.05，选用增广拉格朗日算法，法向刚度因子设为1[10]。主、从动轮轴孔处添加旋转副约束，主动轮施加转速，从动轮施加阻力矩。转速和扭矩计算方法见文献[11]，本文中健康齿轮和故障齿轮（指含0.8L-0.5H齿根裂纹的从动锥齿轮）的主动锥齿轮转速n和从动锥齿轮的扭矩T如表3所示。

表3 3节径行波共振转速和扭矩

2.2 行波共振状态下的瞬态动力学分析

求解设置中，时间为9×10-5s，初始子步设置为14。依据上述设置进行健康齿轮和故障齿轮3节径行波共振状态下的瞬态动力学分析，提取关注区域的应力值。健康及故障齿轮应力分布如图4所示，齿根处应力变化如图5所示。

图4 3节径行波共振时齿轮应力分布图

图5 随着计算子步数增加齿轮齿根处应力的变化规律

根据图4和图5分析可知：健康齿轮在第1到第14子步内，齿轮齿根应力先缓慢增加后急剧增大，第14子步时达到最大257MPa。当齿轮处于3节径行波共振时齿轮应力分布较大区域包含13个轮齿。含齿根裂纹齿轮在第1到第14子步内，齿轮齿根应力增加较快，第14子步时达到最大1349MPa。当齿轮处于3节径行波共振时齿轮应力分布较大区域包含16个轮齿。

为深入研究裂纹对齿根应力分布的影响，选取故障齿轮上的含裂纹齿根（记为齿根a）和沿从动轮旋转方向相邻齿根（记为齿根b），以及健康齿轮上相同位置的两个齿根（分别记为齿根A和齿根B）如图6所示。不同子步数下故障齿轮齿根与健康齿轮齿根应力比变化趋势如图7所示。

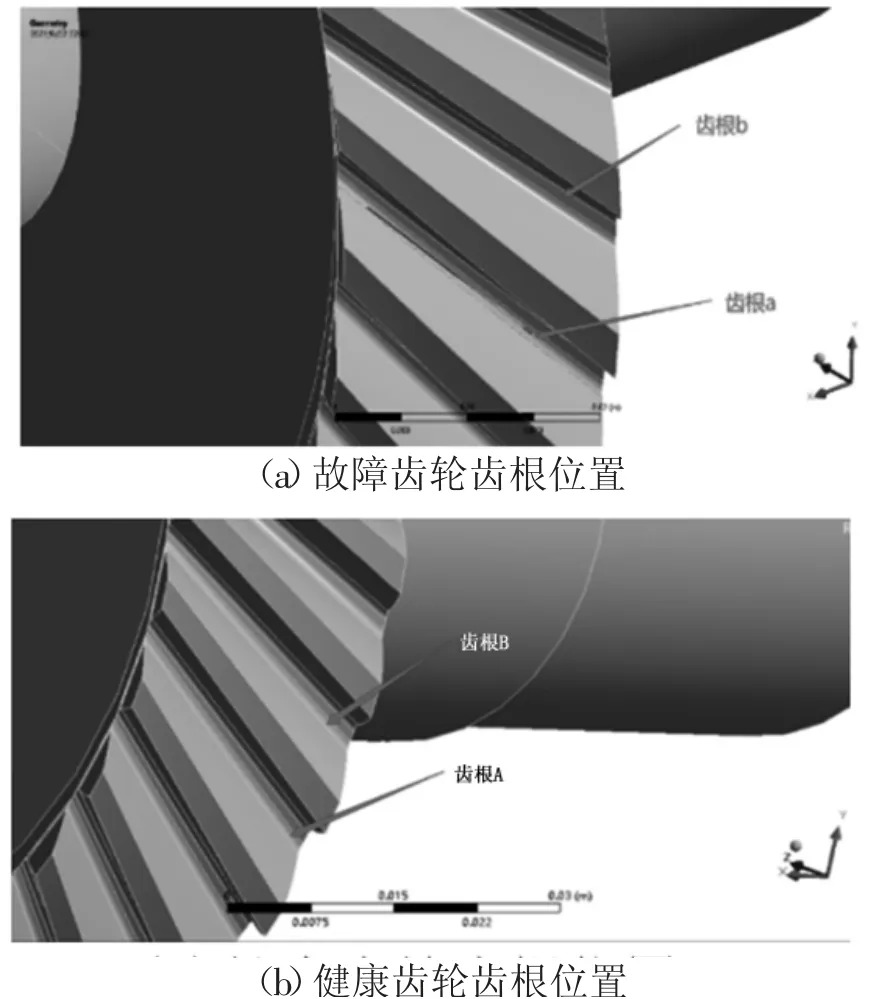
图6 故障齿轮和健康齿轮研究齿根位置

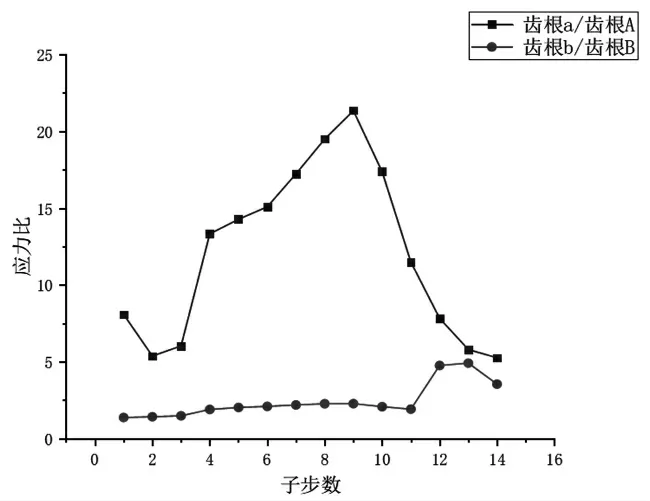
图7 随着计算子步数增加健康齿根与含裂纹齿根应力比变化趋势

由图7分析可知，齿根a与齿根A应力值之比范围为5～21；齿根b与齿根B应力值之比范围为1～5；齿轮3节径前行波共振状态下，故障齿轮含裂纹齿根处应力值与健康齿轮相同位置上的齿根处应力值之比大于故障齿轮健康齿根处应力值与健康齿轮相同位置上的齿根处应力值之比。

3 结论

（1）通过对含有不同长度和深度齿根裂纹的齿轮进行模态分析，可以得到：随着齿轮节径数增加或齿根裂纹尺寸增大，健康齿轮和故障齿轮的固有频率的差异越大。

（2）当中心锥齿轮发生3节径前行波共振时：第1到第14子步内，健康齿轮齿根应力先缓慢增加后急剧增大，故障齿轮齿根应力增加较快；应力分布较大区域健康齿轮包含13个轮齿，故障齿轮包含16个轮齿；裂纹齿根处应力显著增加，其应力值是健康齿轮齿根处应力值的5.8倍；故障齿轮含裂纹齿根处应力值与健康齿轮相同位置上的齿根处应力值之比为5～20，故障齿轮健康齿根处应力值与健康齿轮相同位置上的齿根处应力值之比为1～5。