基于SOLO分类理论的试题分析与教学策略
董友军 彭欢 皮飞鹏


摘 要:以“2021年广东高考物理实验试题”为例,探索基于SOLO分类理论的试题分析与教学策略.科学探究水平与SOLO层次对应:水平1对应单点结构;水平2和水平3对应多点结构;水平4对应关联结构;水平5对应抽象拓展结构.基于SOLO分类理论的教学策略:用“器材发散”突破单点结构试题;用“原理中心”突破多点结构试题;用“知识整合”突破关联结构试题;用“方法迁移”突破抽象拓展结构试题.
关键词:SOLO分类理论;科学探究水平;试题分析;教学策略;实验试题
中图分类号:G633.7 文献标识码:B 文章编号:1008-4134(2021)21-0019-04
基金项目:广州市黄埔区教育科学规划课题“基于学习进阶的中学物理教学设计研究”(项目编号:2020096).
作者简介:董友军(1976-),男,湖南衡阳人,本科,中学高级教师,研究方向:中学物理学科教学;
彭欢(1987-),女,湖南衡阳人,硕士,中学一级教师,研究方向:中学物理学科教学;
皮飞鹏(1965-),男,湖南邵阳人,博士,副教授,硕士生导师,研究方向:物理教育.
物理学科核心素养包括物理观念、科学思维、科学探究、科学态度与责任.科学探究是指基于观察和实验提出物理问题、形成猜想和假设、设计实验与制订方案、获取和处理信息、基于证据得出结论并作出解释,以及对科学探究过程和结果进行交流、评估、反思的能力[1].高考物理试卷中,通过实验试题考查学生的科学探究素养.笔者依据SOLO分类理论分析2021年广东高考物理实验试题,明确高考实验试题“考什么”和“如何考”,有助于高中物理教师把握实验教学的方向,深入思考“教什么”和“如何教”,使得课堂实验教学更有方向、更有效率.
1 SOLO分类理论
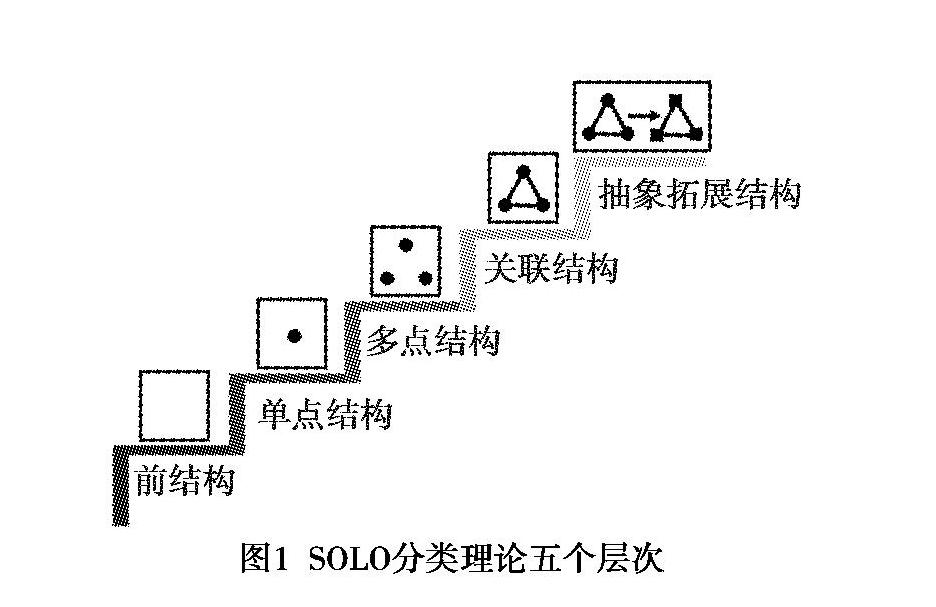
SOLO分类理论是指教育心理学家约翰·彼格斯(John B.Biggs)提出的学习质量评价理论[2].SOLO是英文“structure of the observed learning outcome”的缩写,意为“可观察的学习成果结构”.SOLO分类理论是在皮亚杰发展阶段论基础上建立起来,体现了现代心理学的研究成果,具有严格的理论形态.SOLO分类理论认为,学生回答某个问题时所表现出来的思维结构是可以检测的,而检测焦点不是回答问题的“量”而是回答问题的“质”.SOLO分类理论根据学生回答问题的结果,把学生思维结构分为由浅到深五个层次:前结构层次、单点结构层次、多点结构层次、关联结构层次、抽象拓展结构层次(如图1).
前结构层次是指学生用一些与问题不相关的素材进行回答;单点结构层次是指学生用一项与问题相关的素材进行回答;多点结构层次是指学生用多项与问题相关的素材进行回答,但多项素材彼此独立,不能融会贯通;关联结构层次是指学生将多项与问题相关的素材联系起来,形成一个整体,能够处理复杂问题;抽象拓展结构层次是指学生将多项与问题相关素材综合分析,归纳抽象出新的假设,能对相关知识进行应用与迁移,促使问题的意义得到拓展,具有普遍意义.前三个层次主要体现“量”的积累,而后两个层次追求“质”的提升.
SOLO分类理论能够评价学生的思维结构层次,而高考物理试题需要保证适宜的区分度,因此它们之间存在着对应关系.我们可以用SOLO分类理论对高考试题进行研究,既可以明确高考试题的评价方向,也可以提高课堂的教学效率.
2 科学探究水平与SOLO层次
学业质量是学生在完成本学科课程学习后的学业成就表现.高中物理学业质量根据问题情境的复杂程度、知识和技能的结构化程度、思维方式或价值观念的综合程度等划分为不同水平.每一级水平皆包含物理学科核心素养的四个方面,主要表现为学生在不同复杂程度情境中运用重要概念、思维、方法和观念等解决问题的关键特征.高中物理学业质量分为五级水平,既是教師命题和评价的重要依据,也是高中学业水平考试命题的重要依据,其中学业质量水平2是用于“学考”的命题依据、学业质量水平4是用于“高考”的命题依据.新课程标准对科学探究进行了五个水平的划分,表1给出了科学探究水平与SOLO层次之间的对应关系.
3 基于SOLO分类理论的实验分析
高考实验题设问,按照单点结构、多点结构、关联结构、抽象拓展结构,循序渐进,呈现出从易到难趋势.首问比较易,一般是单点结构或多点结构;末问比较难,一般是关联结构或抽象拓展结构;且设问主要集中在多点结构,抽象拓展结构比较少,具体情况见表2.因此,高考实验题难度中等偏易,有助于减轻学生学习负担.同时引导教师带领学生完成所有课标必做实验,让学生经历实验的完整过程,培养学生的实验操作能力和创新能力.
例题1 (2021年广东高考 11题)某兴趣小组测量一缓冲装置中弹簧的劲度系数.缓冲装置如图2所示,固定在斜面上的透明有机玻璃管与水平面夹角为30°,弹簧固定在有机玻璃管底端.实验过程如下:先沿管轴线方向固定1mm刻度尺,再将单个质量为200g的钢球(直径略小于玻璃管内径)逐个从管口滑进,待弹簧静止,记录管内钢球的个数n和弹簧上端对应的刻度尺示数Ln,数据见表3.实验过程中弹簧始终处于弹性限度内.采用逐差法计算弹簧压缩量,进而计算其劲度系数.
(1)利用ΔLi=Li+3-Li(i=1,2,3)计算弹簧的压缩量:ΔL1=6.03cm,ΔL2=6.08cm,ΔL3=cm,压缩量的平均值ΔL=ΔL1+ΔL2+ΔL33=cm;
(2)上述ΔL是管中增加个钢球时产生的弹簧平均压缩量;
(3)忽略摩擦,重力加速度g取9.80m/s2,该弹簧的劲度系数为N/m(结果保留3位有效数字).
设问(1)是求ΔL3,把已知L6=18.09cm、L3=12.05cm代入公式ΔLi=Li+3-Li(i=1,2,3)即可求得ΔL3=6.04cm,本设问只是“对数据进行初步整理”,属于单点结构层次.
设问(2)是求ΔL,把已知L1=8.04cm、L2=10.03cm、L3=12.05cm、L4=14.07cm、L5=16.11cm、L6=18.09cm代入公式ΔLi=Li+3-Li(i=1,2,3)、ΔL=ΔL1+ΔL2+ΔL33中,可以求得ΔL=6.05cm,本设问也是“对数据进行初步整理”,也属于单点结构层次.
求ΔL表示增加几个钢球,根据公式ΔLi=Li+3-Li(i=1,2,3)、ΔL=ΔL1+ΔL2+ΔL33,可以判断出ΔL表示增加3个钢球,本设问需要“对数据进行整理,得到初步的结论”,属于多点结构层次.
设问(3)是求弹簧的劲度系数,先对3个钢球做受力分析:重力G=3mg、支持力F1、弹力F2=kΔL;再把重力G=3mg分解为平行斜面分力G1=3mgsin30°和垂直斜面分力G2=3mgcos30°;由于弹簧静止,则3个钢球静止,即有G1=F2,解得劲度系数k约为48.595N/m;由于题目要求结果保留3位有效数字,即弹簧的劲度系数为48.6N/m.本设问既需要对3个小钢球进行受力分析、记住重力和弹力公式、对重力进行正交分解、应用二力平衡规律,还需要对3个钢球质量和弹簧压缩量进行单位换算、记住三角函数规律、保留3位有效数字,才可以得到弹簧劲度系数的正确结论,即表示“能用多种方法分析数据,发现规律,形成合理的结论,用已有的物理知识进行科学解释”,属于抽象拓展结构层次.
例题2 (广东高考 12题)某小组研究热敏电阻阻值随温度的变化规律.根据实验需要已选用了规格和量程合适的器材.
(1)先用多用电表预判热敏电阻阻值随温度的变化趋势.选择适当倍率的欧姆档,将两表笔,调节欧姆调零旋钮,使指针指向右边“0Ω”处.测量时观察到热敏电阻温度越高,相同倍率下多用电表指针向右偏转角度越大,由此可判断热敏电阻阻值随温度的升高而.
(2)再按图连接好电路进行测量.
①闭合开关S前,将滑动变阻器R1的滑片滑到端 (选填“a”或“b”).
将温控室的温度设置为T,电阻箱R0调为某一阻值R01.闭合开关S,调节滑动变阻器R1,使电压表和电流表的指针偏转到某一位置,记录此时电压表和电流表的示数、T和R01.断开开关S.
再将电压表与热敏电阻C端间的导线改接到D端,闭合开关S.反复调节R0和R1,使电压表和电流表的示数与上述记录的示数相同,记录此时电阻箱的阻值R02,断开开关S.
②实验中记录的阻值R01R02(选填“大于”“小于”或“等于”),此时热敏电阻阻值RT=.
(3)改变温控室的温度,测量不同温度时的热敏电阻阻值,可以得到热敏电阻阻值随温度的变化规律.
设问(1)是文字填空“将两表笔”,本设问的前面“选择适当的欧姆档”与后面“调节欧姆调零旋钮”之间的逻辑性本不强,需要学生亲自做过这个实验,并记住了该关键的实验步骤,才能够填出正确结果为“短接”,即“能根据已有的科学探究方案,使用基本的器材获得数据”,属于多点结构层次.
设问(2)也是文字填空“由此可判断热敏电阻阻值随温度的升高而”,要正确回答本设问,需要知道多用电表的指针开始停在表盘最左边,表示电阻为无穷大,当指针向右边偏转时,表示电阻减小.由于“观察到热敏电阻温度越高,相同倍率下多用电表指针向右偏转角度越大”,即 “由此可以判断热敏电阻阻值随温度的升高而减小”.要能正确回答本设问,同样需要学生亲自做过这个实验,并记住了多用电表刻度盘数据与指针偏转规律,才可以填出正确结果为“减小”,即“能根据已有的科学探究方案,使用基本的器材获得数据”,属于多点结构层次.
设问(2)的①二选一的选择填空“闭合开关S前,将滑动变阻器R1的滑片滑到端(选填“a”或“b”)”,要正确选择b,就需要看懂滑动变阻器的连接结构,才能保证在闭合开关S前,让滑动变阻器接入电路的电阻值最大,即“能根据已有的科学探究方案,使用基本的器材获得数据”,属于多点结构层次.
设问(2)的②是三选一的选择填空、设问(3)是求出热敏电阻阻值RT的表达式,要正确选择设问(2)的②,就要先求得设问(3).这就需要知道电压表、电流表、电阻箱的测量原理,还要记住部分电路欧姆定律及电阻串联并联规律,并理解电路结构,才能够得出:u=I(RA+R01),u=I(RA+R02+RT),从而求得设问(3)是RT=R01-R02,进而得出设问(2)的②正确选择是大于.即“能分析数据,发现其中规律,形成合理的结论,用已有的物理知识进行解释”,属于关联结构层次.
4 基于SOLO分类理论的教学策略
教学策略是指在教学过程中,为了完成教学目标,依据教学的主客观条件,特别是学生的实际情况,对所用的教学顺序、活动程序、组织形式、教学方法和教学媒体等的总体考虑.通俗地说,教学策略就是教学各个环节遵循的思想和方法.根据实验题分析,笔者对实验教学提出以下四点教学策略.
4.1 策略1——用“器材发散”突破单点结构试题
器材是物理实验的基础,没有器材就没有实验.做实验离不开器材的选取与使用,测量同一个物理量,可以采用发散思维,选用不同的器材.例如,测量长度,可以用传统器材——米尺、卷尺等测量,也可以用现代器材——螺旋测微器、游标卡尺、位移传感器、声纳、雷达等测量.通过运用不同的测量工具,既可以熟悉各种器材的操作规范,也可以拓宽学生视野,从而突破单点结构试题.
4.2 策略2——用“原理中心”突破多点结构试题
原理是指實验所用到的规律或公式,原理是实验的出发点.在实验教学时,对于一个物理量要创设多种不同的公式去解决.如求加速度,可以直接用公式a=v2-v1t12测量,也可以间接用原理v22-v21=2ax、x=v0t+12at2、x2-x1=at2、a=v2r、F=ma等测量.原理也是解决问题的归宿点,一旦确定了实验原理,即解决实验问题都要从原理去思考.高考实验题设计,都是以原理为中心,依据原理选取器材、组合装置、确定步骤、处理数据、分析误差等.如用Δx=x2-x1=at2测量加速度,就可以围绕该公式去分析问题和解决问题.学生抓住了实验原理,就抓住了实验本质,无论怎么考查,只要从原理上去思考,就找到了解题方向,突破了多点结构试题.
4.3 策略3——用“知识整合”突破关联结构试题
知识整合也叫知识系统化,即把有关联的知识组合成网状结构.其作用是既有利于已有知识的理解深化,也有利于头脑中的新旧知识发生相互作用.系统化后的知识也是理解新知识的有力工具,还有利于扩大认识潜力,用深入联系的眼光看待事物.知识之间总是相互联系,通过知识整合,让知识之间的联系清晰化,有助于学生灵活应用物理知识,突破关联结构试题.如测量灯泡的伏安特性曲线,可以整合相关的电压、电流、电阻、电热、电功率知识,见表4.
4.4 策略4——用“方法迁移”突破抽象拓展结构试题
实验教学要以科学方法中心论为指导,构建知识逻辑结构,如图4所示.由图可知,从科学现象出发,必须经过科学方法的加工整理才能获得科学知识,科学方法是科学现象通达科学知识的必经之路,学生只有掌握了科学方法,才能快捷地获取科学知识.科学方法可以分为思维方法和学科方法.学科方法包括获得知识的方法和应用知识的方法,属于强认知方法,体现学科特点,可迁移性弱;思维方法包括逻辑思维方法和非逻辑思维方法,属于弱认知方法,贯穿各门学科,可迁移性强.高考实验题,源于教材也高于教材,都能从教材的实验,得到解题启发,找到解题方法,所以教师在教学中,要认真完成教材的所有实验,包括學生实验和演示实验,既要向学生讲清实验本身的原理,也要向学生介绍实验器材的原理;既要要求学生动手操作实验过程,也要要求学生掌握数据处理方法.如用逐差法求弹簧压缩量,用正交分解法、二力平衡法求弹簧弹力.通过方法的总结归纳,让学生掌握方法的一般性规律,实现方法迁移,突破抽象拓展结构试题.
5 结束语
SOLO分类理论的层次与科学探究的水平对应,用SOLO分类理论分析高考实验试题,不但可以把握高考命题的特点与趋势,还可以指导高考实验教学的难度与方向,从而达到理顺教考关系,实现“以考促教、以考促学”的目的[3],并促进立德树人根本任务的落实,发展学生物理学科核心素养.
参考文献:
[1]中华人民共和国教育部.普通高中物理课程标准(2017年版)[M].北京:人民教育出版社,2018.
[2]John B.Biggs等著,高凌飚等译.学习质量评价:SOLO分类理论(可观察的学习成果结构)[M].北京:人民教育出版社,2018.
[3]中华人民共和国教育部.普通高中物理课程标准(2017年版)[M].北京:人民教育出版社,2018.
[4]中华人民共和国教育部.普通高中物理课程标准(2017年版)[M].北京:人民教育出版社,2018.
[5]中华人民共和国教育部.普通高中物理课程标准(2017年版)[M].北京:人民教育出版社,2018.
[3]教育部考试中心.中国高考评价体系[M].北京:人民教育出版社,2019.
(收稿日期:2021-06-30)

