自动驾驶车辆轨迹跟踪控制算法研究

宋吉超 周成才 宋卓宇

摘要：在智能车辆的自动驾驶系统中，需要采用合适的控制算法，控制自动驾驶车辆沿预先规划的轨迹运行。本文基于车辆的运动学模型，分析了自动驾驶车辆轨迹跟踪控制的纯跟踪算法（Pure Pursuit）。通过纯跟踪算法控制车辆后轮的运动轨迹，实现了调整车辆当前位置与规划轨迹之间的偏差，从而使车辆达到了跟踪预设轨迹的效果。并且分析了车辆跟踪过程中，速度调节系数对跟踪效果的影响，验证了纯跟踪算法的有效性与精确性。

Abstract： In the automatic driving system of intelligent vehicle， it is necessary to adopt appropriate control algorithm to control the automatic driving vehicle along the pre-planned trajectory line. Based on the vehicle kinematics model， this paper analyzes Pure Pursuit algorithm for trajectory tracking control of autonomous vehicle. By using the Pure Pursuit algorithm for trajectory tracking control of autonomous vehicle. By using the Pure Pursuit algorithm to control the trajectory of the rear wheel of the vehicle， the deviation between the current position of the vehicle and the planned trajectory can be adjusted， so that the vehicle can track the preset trajectory. In addition， the influence of the speed adjustment coefficient on the tracking effect in the process of vehicle tracking is analyzed， and the effectiveness and accuracy of the Pure Pursuit algorithm are verified.

关键词：自动驾驶;轨迹跟踪;纯跟踪算法;物联网技术

Key words： automatic driving;trajectory tracking;pure pursuit algorithm;internet of things technology

中图分类号：U461.1                                   文献标识码：A                                  文章編号：1674-957X（2021）23-0215-02

0  引言

智能车辆的自动驾驶系统是一项集成多学科复杂技术，该系统通常采用定位-感知-规划-决策-控制这一技术路线来完成相关任务。自诞生以来，自动驾驶被认为是解决道路安全事故、交通拥堵等问题的良好方案。特别是近几年，随着新能源汽车及物联网技术的普及，自动驾驶车辆成为汽车行业大力发展的新方向。毫不夸张的说，具有自动驾驶功能的智能车辆是未来工业界最大的风口之一。

1  车辆运动学模型

要控制车辆的运动，首先要对车辆的运动建立数字化模型，模型建立的越准确，对车辆运动的描述越准确，对车辆的跟踪控制的效果就越好。除了真实反映车辆特性外，建立的模型也应该尽可能的简单易用。车辆模型一般分为运动学和动力学模型。其中车辆运动学模型把车辆完全视为刚体，主要考虑车辆的位姿、速度、前轮转角等的关系，不考虑任何力的影响。车辆运动学模型常采用二自由度自行车模型，基于如下假设：①不考虑车辆在垂直方向的运动，即假设车辆的运动是一个二维平面上的运动。②假设车辆左右侧轮胎在任意时刻都拥有相同的转向角度和转速;这样车辆的左右两个轮胎的运动可以合并为一个轮胎来描述。③假设车辆行驶速度变化缓慢，忽略前后轴载荷的转移。④假设车身和悬架系统都是刚性系统。⑤假设车辆的运动和转向是由前轮驱动（front-wheel-only）的。

则简化后的车辆二自由度模型如图1所示。

2  纯跟踪算法

2.1 纯跟踪算法概述

纯跟踪控制算法（Pure Pursuit）是一种典型的横向控制方法，最早由 R. Wallace 在1985年提出，该方法的本质是基于几何原理对车辆的运动轨迹进行控制，对外界的鲁棒性较好，即受外界各种干扰的影响较小。

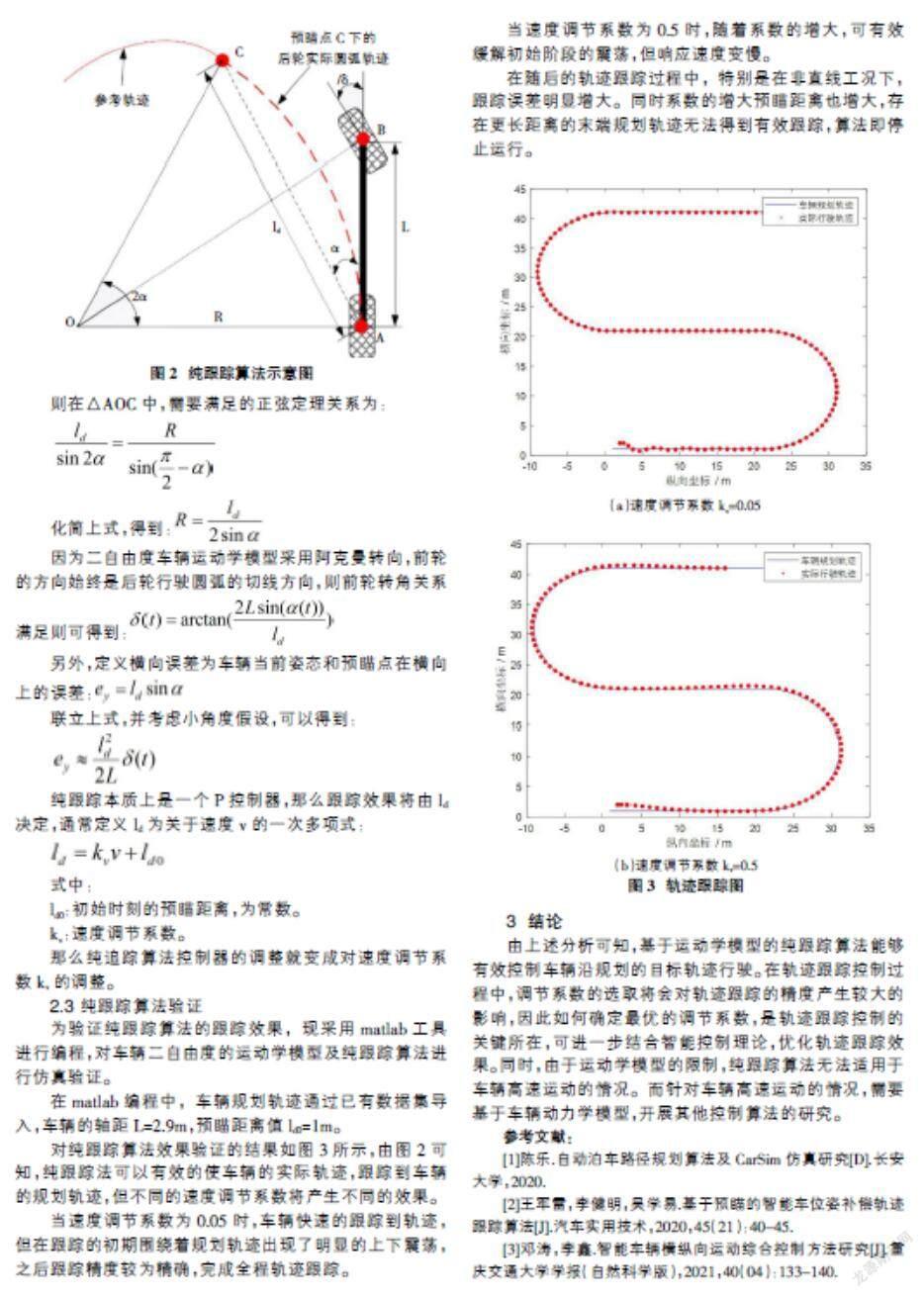
该算法的思想：基于当前车辆后轮中心位置，在参考路径上向ld（自定义）的距离匹配一个预瞄点，假设车辆后轮中心点可以按照一定的转弯半径行驶抵达该预瞄点，然后根据预瞄距离ld、车辆的转弯半径、记忆车辆坐标系下预瞄点的朝向角之间的几何关系来确定前轮转角。纯跟踪算法示意图如图2所示。

2.2 纯跟踪算法原理

为了使车辆后轮跟踪圆弧虚线轨迹到达C点，已知几何关系：■

■

则在△AOC中，需要满足的正弦定理关系为：

■

化简上式，得到：■

因为二自由度车辆运动学模型采用阿克曼转向，前轮的方向始终是后轮行驶圆弧的切线方向，则前轮转角关系满足则可得到：■

另外，定义横向误差为车辆当前姿态和预瞄点在横向上的误差：■

联立上式，并考虑小角度假设，可以得到：

■

纯跟踪本质上是一个P控制器，那么跟踪效果将由ld决定，通常定义ld为关于速度v的一次多项式：

■

式中：

ld0：初始时刻的预瞄距离，为常数。

kv：速度调节系数。

那么纯追踪算法控制器的调整就变成对速度调节系数kv的调整。

2.3 纯跟踪算法验证

为验证纯跟踪算法的跟踪效果，现采用matlab工具进行编程，对车辆二自由度的运动学模型及纯跟踪算法进行仿真验证。

在matlab编程中，车辆规划轨迹通过已有数据集导入，车辆的轴距L=2.9m，预瞄距离值ld0=1m。

對纯跟踪算法效果验证的结果如图3所示，由图2可知，纯跟踪法可以有效的使车辆的实际轨迹，跟踪到车辆的规划轨迹，但不同的速度调节系数将产生不同的效果。

当速度调节系数为0.05时，车辆快速的跟踪到轨迹，但在跟踪的初期围绕着规划轨迹出现了明显的上下震荡，之后跟踪精度较为精确，完成全程轨迹跟踪。

当速度调节系数为0.5时，随着系数的增大，可有效缓解初始阶段的震荡，但响应速度变慢。

在随后的轨迹跟踪过程中，特别是在非直线工况下，跟踪误差明显增大。同时系数的增大预瞄距离也增大，存在更长距离的末端规划轨迹无法得到有效跟踪，算法即停止运行。

3  结论

由上述分析可知，基于运动学模型的纯跟踪算法能够有效控制车辆沿规划的目标轨迹行驶。在轨迹跟踪控制过程中，调节系数的选取将会对轨迹跟踪的精度产生较大的影响，因此如何确定最优的调节系数，是轨迹跟踪控制的关键所在，可进一步结合智能控制理论，优化轨迹跟踪效果。同时，由于运动学模型的限制，纯跟踪算法无法适用于车辆高速运动的情况。而针对车辆高速运动的情况，需要基于车辆动力学模型，开展其他控制算法的研究。

参考文献：

[1]陈乐.自动泊车路径规划算法及CarSim仿真研究[D].长安大学，2020.

[2]王军雷，李健明，吴学易.基于预瞄的智能车位姿补偿轨迹跟踪算法[J].汽车实用技术，2020，45（21）：40-45.

[3]邓涛，李鑫.智能车辆横纵向运动综合控制方法研究[J].重庆交通大学学报（自然科学版），2021，40（04）：133-140.