“公式法”突破晶体计算难点问题

王志刚

高考中选修3《物质结构与性质》的考查，难点集中在晶体计算方面，学生在复习备考中遇到的问题主要表现在以下三个方面：

（1）如何计算？

（2）如何找几何关系？

（3）如何进行单位换算？

解决好了这三个问题，晶体计算的难点，也就基本突破了。

下面以近3年高考试题中晶体计算问题为研究对象，分析研究，寻找晶体计算问题的一般解题思路和办法。

例题 （2020年全国理综卷Ⅲ题35，节选）（4）研究发现，氮硼烷（NH3·BH3）在低温高压条件下为正交晶系结构，晶胞参数分别为a pm、b pm、c pm，α=β=γ=90°。氨硼烷的2×2×2超晶胞结构如图1所示。

氨硼烷晶体的密度ρ=g·cm-3（列出计算式，设NA为阿伏加德罗常数的值）。

解析 观察氨硼烷2×2×2超晶胞结构，可以发现该结构中含有16（4×4）个氮硼烷微粒，即Z=16，运用公式进行如下计算：

ρ=ZMVNA

=16×312a×10-10×2b×10-10×2c×10-10NA

=62abc×10-30NA

总结 晶体计算问题的一般解题思路：

（1）灵活运用公式M=m（微粒）×NA=ρVZ×NA（或ρ=ZMVNA）进行计算。

①M：微粒的摩尔质量;

②Z：一个晶胞（或结构单元）中含有的微粒个数;

③V：一个晶胞（或结构单元）的体积;

④NA：阿伏加德罗常数。

（2）知道常见两点间距离的计算方法，能进行基本几何分析与计算（注意勾股定理在计算中的使用）。

①体心立方，两原子间最短距离：d=32a;

②面心立方，两原子间最短距离：d=22a;

③其余则根据几何关系进行计算。

（3）計算时要特别注意单位换算问题。

①1 pm=10-12m=10-10cm

②1 nm=10-9m=10-7cm

巩固 （2019年全国理综卷Ⅰ题35，节选）

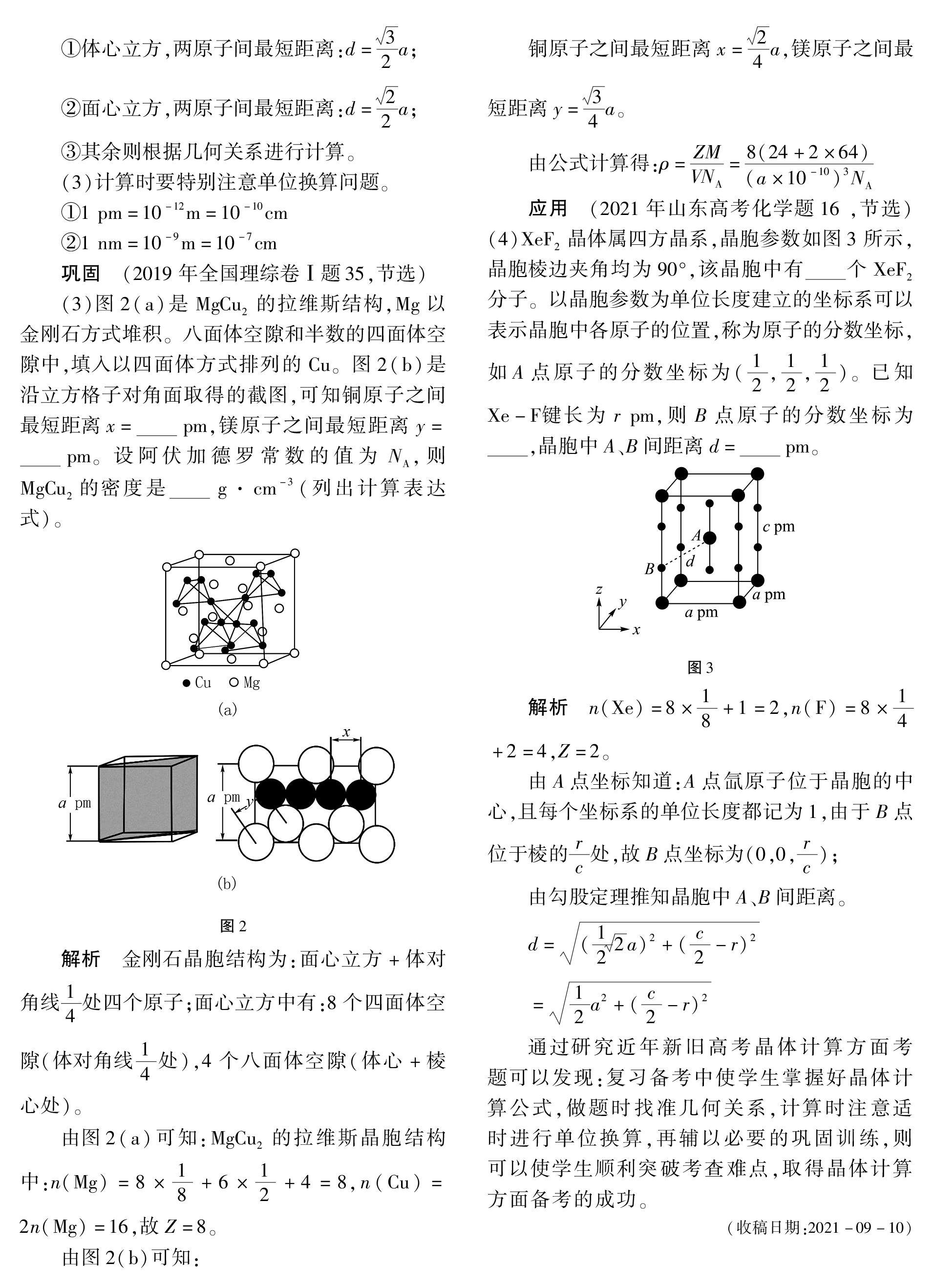
（3）图2（a）是MgCu2的拉维斯结构，Mg以金刚石方式堆积。八面体空隙和半数的四面体空隙中，填入以四面体方式排列的Cu。图2（b）是沿立方格子对角面取得的截图，可知铜原子之间最短距离x=pm，镁原子之间最短距离y=pm。设阿伏加德罗常数的值为NA，则MgCu2的密度是g·cm-3（列出计算表达式）。

解析 金刚石晶胞结构为：面心立方+体对角线14处四个原子;面心立方中有：8个四面体空隙（体对角线14处），4个八面体空隙（体心+棱心处）。

由图2（a）可知：MgCu2的拉维斯晶胞结构中：

n（Mg）=8×18+6×12+4=8，n（Cu）=2n（Mg）=16，故Z=8。

由图2（b）可知：

铜原子之间最短距离x=24a，镁原子之间最短距离y=34a。

由公式计算得：ρ=ZMVNA=8（24+2×64）（a×10-10）3NA

应用 （2021年山东高考化学题16 ，节选）（4）XeF2晶体属四方晶系，晶胞参数如图3所示，晶胞棱边夹角均为90°，该晶胞中有个XeF2分子。以晶胞参数为单位长度建立的坐标系可以表示晶胞中各原子的位置，称为原子的分数坐标，如A点原子的分数坐标为（12，12，12）。已知Xe-F键长为r pm，则B点原子的分数坐标为，晶胞中A、B间距离d=pm。

解析 n（Xe）=8×18+1=2，n（F）=8×14+2=4，Z=2。

由A点坐标知道：A点氙原子位于晶胞的中心，且每个坐标系的单位长度都记为1，由于B点位于棱的rc处，故B点坐标为（0，0，rc）;

由勾股定理推知晶胞中A、B间距离。

d=（122a）2+（c2-r）2=12a2+（c2-r）2

通过研究近年新旧高考晶体计算方面考题可以发现：复习备考中使学生掌握好晶体计算公式，做题时找准几何关系，计算时注意适时进行单位换算，再辅以必要的巩固训练，则可以使学生顺利突破考查难点，取得晶体计算方面备考的成功。

（收稿日期：2021-09-10）