基于改进模糊物元分析法的用水效率评价

冷东升

摘要：为了使用水效率评价方法更具适用性，结合灰色系统理论，对模糊物元评价法中的欧式贴近度进行了改进，并利用待评物元在标准物元上的投影值大小进行评价;同时，耦合CRITIC赋权法，构建了水资源利用效率评价模型。在此基础上，以绍兴市为例，对该市的水资源利用效率进行评价。评价结果表明：绍兴市下辖的各县（市、区）水资源利用效率高低排序为诸暨市>越城区>上虞区>嵊州市>柯桥区>新昌县，该结果符合绍兴市的实际情况，说明构建的水资源利用效率評价模型具有一定的实用性和可操作性。

关键词：水资源利用效率评价模型; 模糊物元分析法; CRITIC法; 灰色关联投影值; 欧式贴近度; 绍兴市

中图法分类号： TV213

文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2021.11.016

0引 言

近年来，国家为了加强对水资源利用效率的控制管理，出台了《国家节水行动方案》，大力推动全社会节水。用水效率是最严格水资源管理制度的核心内容，对其进行科学合理的评价是开展用水效率管控工作的前提[1]。

目前，国内外许多专家学者开展了用水效率评价的相关研究。李绍飞[2]运用模糊物元模型评价了天津市里自沽灌区的农业用水效率;买亚宗等[3]运用DEA方法构建了中国工业水资源利用效率评价模型，用于分析中国30个省份的工业用水效率;岳俊涛等[4]运用CRITIC赋权法耦合TOPSIS评价法，对江西省各地市的用水效率进行了评价。

水资源利用效率评价具有模糊性和随机性[5]，模糊物元评价法在解决这类问题时具有一定的优势。该方法是将事物的多属性综合成一个整体进行评价，即根据待评样本与标准样本“接近”的程度评价样本的优劣。因此，如何确定待评样本与标准样本“接近”的程度已然是影响该方法评价结果的关键。现有成果多数是采用“欧式贴近度”来度量“接近”程度，但是它仅考虑了待评样本与标准样本向量终点的距离，不能反映两者变化趋势的一致性。因此，本文在现有研究的基础上，利用灰色关联投影法改进“欧式贴近度”[6]，并结合CRITIC赋权法，构建了区域水资源利用效率评价模型。在此基础上，以绍兴市为例，比较科学、客观地评价了绍兴市的用水效率，本文研究成果可为用水效率评价提供一个新的思路。

1理论基础

2应用实例

2.1研究区概况

绍兴市是浙江省辖地级市，位于浙江省中北部、杭州湾南岸，是具有江南水乡特色的文化和生态旅游城市、长三角城市群的重要城市、环杭州湾大湾区核心城市。绍兴市东连宁波市，南临台州市和金华市，西接杭州市，北隔钱塘江与嘉兴市相望，全市面积为8 279 km2，下辖3区2市1县。绍兴市水资源总量丰富，但人均水资源量低于全省和全国的平均水平，不足1 200 m3。提高水资源利用效率是贯彻落实习总书记“节水优先”治水方针、解决“水乡缺水”问题的必要措施。

2.2评价指标体系构建

目前，涉及用水效率评价的指标体系众多，本文在前人研究的基础上[13-15]，本着科学、合理、客观、全面的宗旨，分别从综合、生活、工业、农业用水等4个方面，选取了万元GDP用水量、人均综合用水量、城镇居民人均生活用水量、农村居民人均生活用水量、万元工业增加值用水量、工业用水重复利用率、亩均灌溉用水量和单方水农业产值等8个指标，构建了水资源利用效率评价指标体系（见表1）。

本文研究对象为绍兴市3区2市1县，对其2018年的水资源利用效率进行研究，研究数据均来自于《绍兴市水资源公报》和《绍兴市统计年鉴》中的统计数据。

2.3绍兴市水资源利用效率评价

将绍兴市下辖的3区2市1县分别看作是本次水资源利用效率评价的不同对象M，将各评价指标分别看作是特征C，将指标值看作特征C的量值V，则形成含6个待评对象和8个特征属性的复合物元。根据表1的评价指标体系和2018年《绍兴市水资源公报》以及《绍兴市统计年鉴》等资料，整理得到绍兴市水资源利用效率评价指标样本值，如表2所列。

（1） 确定评价物元。根据表1和表2构建待评价的复合模糊物元，根据公式（3）和公式（4），对表1和表2中的复合物元特征量值归一化，从而得到从优隶属度模糊物元R6×8：

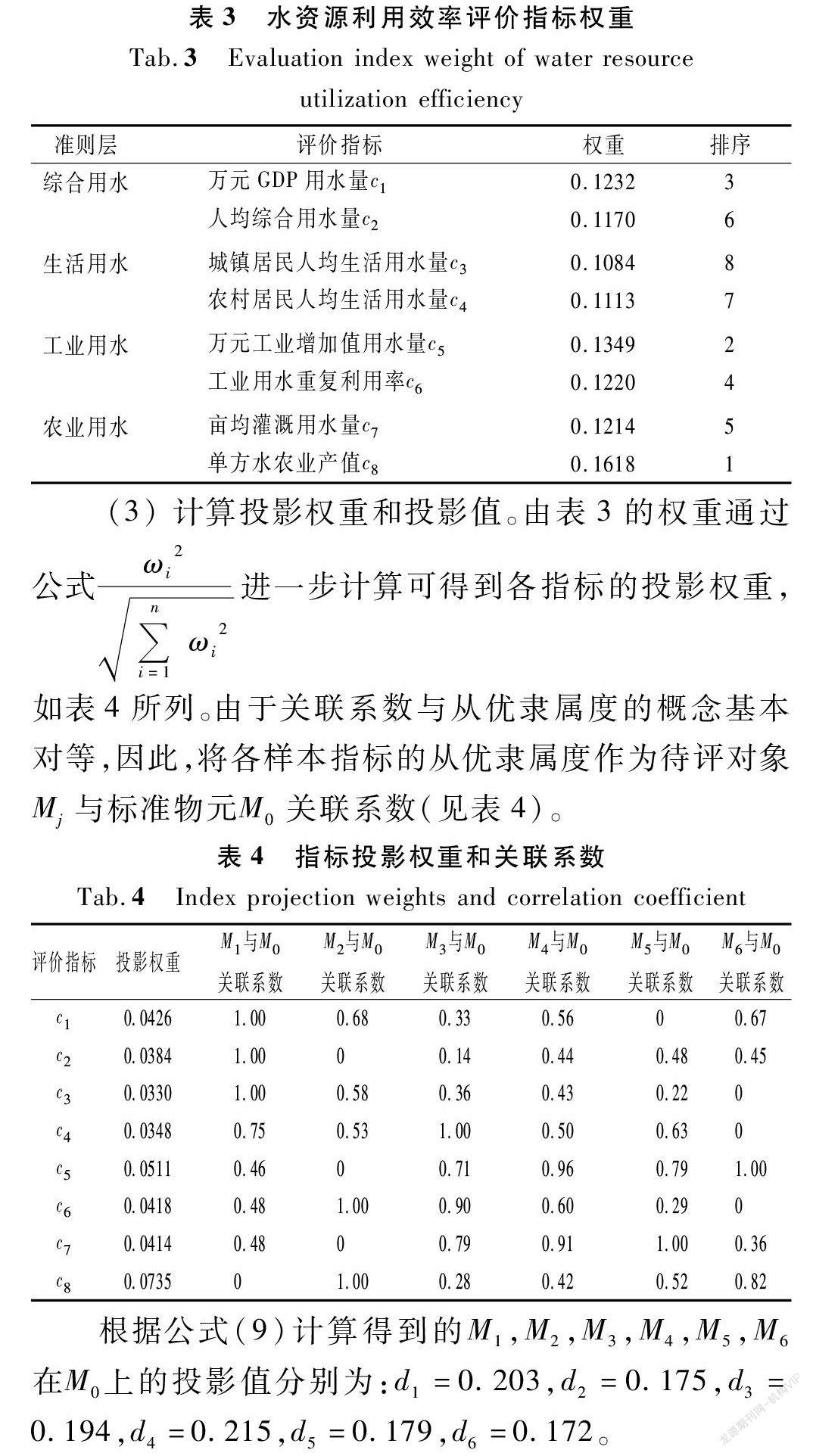
（2） CRITIC法计算指标权重。根据选取的绍兴市2018年各县（市、区）的指标数据，经归一化处理后，根据公式（5）～（7）编写Matlab程序，并运用CRITIC法计算各指标的客观权重，如表3所列。该指标权重综合考虑了指标的变异性和冲突性，指标的变异性和冲突性越大，则指标的权重越大。由表3可知：单方水农业产值、万元工业增加值用水量和万元GDP用水量这3个指标的权重最大，说明这3个指标数据的变异性和冲突性最大，相应地对绍兴市水资源利用效率的影响也最大。其中，万元工业增加值用水量和万元GDP用水量属于最严格水资源管理制度考核指标，单方水农业产值反映农业用水效能，能反映水资源利用效率的实际情况。

（3） 计算投影权重和投影值。由表3的权重通过公式ωi2ni=1ωi2进一步计算可得到各指标的投影权重，如表4所列。由于关联系数与从优隶属度的概念基本对等，因此，将各样本指标的从优隶属度作为待评对象Mj与标准物元M0关联系数（见表4）。

2.4评价结果及分析

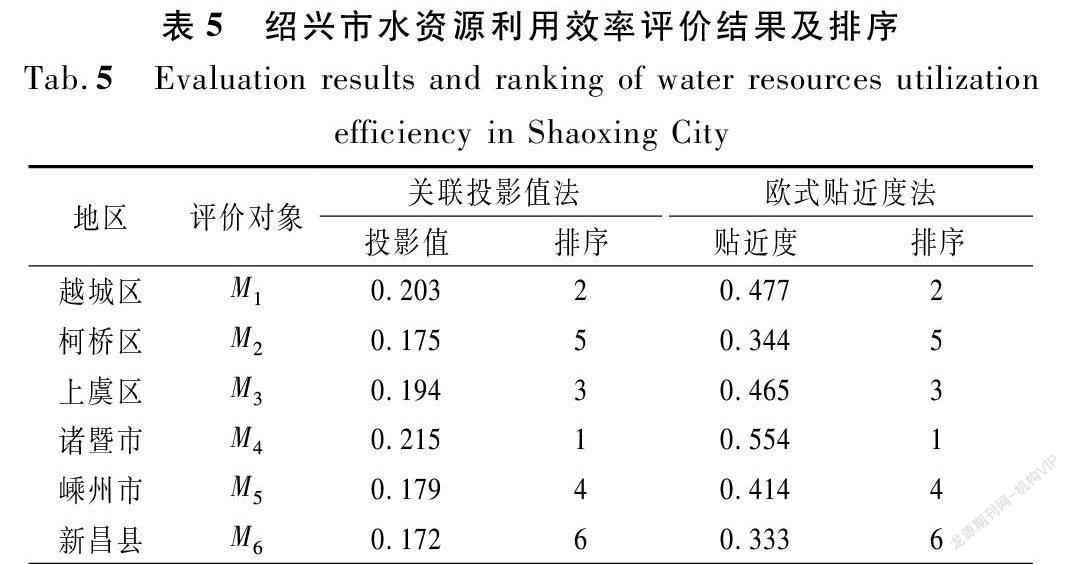
通过计算待评物元在标准物元上的投影值，即可得到绍兴市各县（市、区）水资源利用效率评价的排序情况，并将其与基于欧式贴近度的物元分析法计算成果进行对比，具体如表5所列。

由表5可知：基于关联投影值法的模糊物元分析法计算成果与基于欧式贴近度法的模糊物元分析法的计算成果基本一致，因此，基于关联投影值法的模糊物元分析法具有可操作性和实用性，可用于区域水资源利用效率评价。同时，由评价结果可知：尽管针对该案例的2种方法计算得到的各县市区的排序一致，但从计算原理角度来看，欧式贴近度反映的是2个加权复合模糊物元向量终点间的距离，而关联投影值法反映的是待评物元向量在标准物元向量方向上的接近程度，当2个向量终点距离相等时，关联投影值法更能全面准确地反映各待评物元与标准物元之间的接近程度，所以基于关联投影值法的模糊物元分析法在一定程度上比基于欧式贴近度法的模糊物元分析法更有优势。

评价结果表明，绍兴市各县（市、区）水资源利用效率高低排序为：诸暨市>越城区>上虞区>嵊州市>柯桥区>新昌县，这一评价结果与绍兴市水资源利用情况基本吻合。

3结 论

（1） 将基于关联投影值的物元分析法应用于区域水资源利用效率评价中，引用CRITIC法进行权重计算，建立了基于CRITIC-关联投影值的模糊物元分析法。该模型的建立为水资源利用效率评价提供了一种新的思路。

（2） 引入CRITIC法，综合考虑指标的变异性和冲突性，客观反映了各指标间的权重系数。

（3） 通过关联投影值改进欧式贴近度，将物元样本看作向量，把待评物元模的大小和待评物元与标准物元变化的一致性结合起来，从而全面反映各待评物元与标准物元的贴近程度。

基于上述分析方法，本文以绍兴市为例进行了验证。验证结果显示，上述方法的计算成果与基于欧式贴近度法的计算成果基本一致，这也符合绍兴市的实际情况，说明本文提出的评价方法在水资源利用效率评价中具有很好的实用性和可操作性，具有一定的应用价值。

参考文献：

[1]徐冬梅，徐梦臣，王文川，等.基于改进灰靶模型的水资源利用效率评价[J].水资源研究，2019，8（4）：335-341.

[2]李绍飞.改进的模糊物元模型在灌区农业用水效率评价中的应用[J].干旱区资源与环境，2011，25（11）：175-181.

[3]买亚宗，孙福丽，石磊，等.基于DEA的中国工业水资源利用效率评价研究[J].干旱区资源与环境，2014，28（11）：42-47.

[4]岳俊涛，鄢笑宇，刘启阳.基于CRITIC-TOPSIS方法的江西省用水效率评价研究[J].江西水利科技，2019，45（4）：275-279.

[5]宋岩，刘群昌，江培福.基于改进AHP模糊物元模型的农业用水效率评价[J].人民长江，2013，44（22）：30-33.

[6]梁瑛，季宪军.基于灰色关联投影值的模糊物元评价法的改进[J].统计与决策，2018，34（6）：61-64.

[7]蔡文.从物元分析到可拓学[J].吕梁学刊，1996（2）：1-9.

[8]王梅，唐德善，孟珍珠，等.基于模糊物元的综合评价模型在区域人水和谐评价中的应用[J].水电能源科学，2015，33（2）：160-163，134.

[9]张先起，梁川.基于熵权的模糊物元模型在水质综合评价中的应用[J].水利学报，2005（9）：1057-1061.

[10]汪顺生，黄天元，陈豪，等.基于CRITIC赋权的模糊綜合评判模型在水质评价中的应用[J].水电能源科学，2018，36（6）：48-51.

[11]张玉，魏华波.基于CRITIC的多属性决策组合赋权方法[J].统计与决策，2012（16）：75-77.

[12]马冬梅，陈大春.基于欧式贴近度的模糊物元模型在水资源脆弱性评价中的应用[J].南水北调与水利科技，2015，13（5）：1003-1007.

[13]雷梦婷.SFLA-PP模型在区域水资源利用效率综合评价中的应用[J].长江科学院院报，2017，34（11）：27-32.

[14]黄显峰，李宛谕，方国华，等.基于SPA和云理论的水资源承载能力评价研究[J].华北水利水电大学学报（自然科学版），2019，40（1）：9-15，63.

[15]罗勇，王乐志，傅春，等.基于主客观耦合的区域水资源综合利用效率评价[J].人民长江，2019，50（12）：80-84.

（编辑：赵秋云）

Abstract：To make the efficiency evaluation of water resources utilization more applicable，we improve the Euclidean closeness in the fuzzy matter-element evaluation method based on gray system theory.The projection value of evaluating matter-element on the standard matter-element was used to evaluate the efficiency，while coupled with CRITIC weight method to build a water resources use efficiency evaluation model.Taking Shaoxing City as an example，the evaluation results show that the order of water resources utilization efficiency of each county （city，district） in Shaoxing City is： Zhuji City > Yuecheng District > Shangyu District > Shengzhou City > Keqiao District > Xinchang County.The results are in line with the actual situation of Shaoxing City，which shows that the model has certain practicability and operability.

Key words：water resources utilization efficiency evaluation model;fuzzy matter element;CRITIC method;gray correlation projection value;Euclidean closeness;Shaoxing City