多目标时间序列混合特征动态变权组合预测研究

董志学 宫越 胡勇 甘孟壮

摘  要：在通过LightGBM、Prophet、HotWinters等单一预测算法，以及通过引入搜索指数等消费者行为数据作为预测变量等无法达到汽车品牌销量预测精度的情况下，基于销量数据特征遴选出HotWinters、Prophet、LightGBM三个预测模型，并自主构建了Musgrave方法，以此四个算法构建了组合预测模型，并结合熵值法作为权重动态变化的方法，构建了“动态变权组合预测策略”。本策略使用“单地区多品牌维度、多品牌维度、多地区多品牌维度”三种方式进行六期预测并检验预测效果，结果表明三种方式预测误差中位数分别为7.50%、6.11%、9.61%，因此，本策略能够满足对具有复杂多变特征的数据进行预测的需要。

关键词：动态变权;组合预测;Musgrave;熵值法

中图分类号：TP311     文献标识码：A

Abstract： Prediction accuracy of automobile brand sales cannot be achieved through single prediction algorithms such as LightGBM， Prophet， HotWinters， and the introduction of consumer behavior data such as search indexes as predictors. Based on the characteristics of sales data， this paper proposes to select three predicting models， LightGBM， HotWinters and Prophet， and independently build Musgrave method. With these four algorithms， a combined forecasting model is constructed， and a "dynamic variable weight combination predicting strategy" is constructed by taking the entropy method as a method of dynamic weight change. This strategy uses three methods of "single-region multi-brand dimension， multi-brand dimension， and multi-regional and multi-brand dimensions" to conduct six-period predictions and test the prediction results. Results show that the median prediction errors of the three methods are 7.50%， 6.11%， 9.61%. Therefore， this strategy can meet the needs of predicting data with complex and changeable characteristics.

Keywords： dynamic variable weight; combined prediction; Musgrave; entropy method

1   引言（Introduction）

作为我国最重要的产业部门之一，汽车产业无论横向还是纵向都跨越多个行业部门，同时又与百姓生活关联紧密，对汽车市场销量态势进行准确预测有助于从国家层面洞察各个汽车品牌的经营态势，也有利于从消费者方面了解不同价值等级消费者选择不同汽车品类过程中体现出来的消费结构和能力的变迁。然而，汽车销量数据除了具有周期性（如车型换代）、季节性（如金九银十）、节假日（如春节）等特征，还容易受政府调控（如限行限号、车险费率改革）、车企不定期促销、优惠措施（如购置税减半）等行为的影响，同时又具有随机性特征，而现在新兴的直播购车等互联网形式的营销活动又进一步增加了预测的复杂性。

为提升预测精度，有关学者分别从应用并改进人工智能算法[1]、引入搜索指數等消费者行为数据作为变量[2]等方面进行预测研究。虽然此类方法能够在特点品牌[3]、特定时段[4]产生较高的预测精度，但更多实践表明，使用ARIMA、X-11、HotWinters等时间序列预测方法难以覆盖全部的数据特征，预测结果容易出现“有时准”但难以做到“实时准”，而当今流行的Prophet、LightGBM等机器学习算法具有难以将数据全部特征提取完全的弊端。所以，在单一静态预测无法满足需要的前提下，动态组合预测成为一种改善单项模型预测性能的有效策略。

本文基于相关学者的研究成果，在组合预测的基础上引入动态变权的策略，以广东地区30大品牌销量数据为基础，在数据特征识别、预测模型动态选择依据、各算法价值权重的自动调整方面进行预测研究。同时，为进一步验证动态变权组合预测策略的有效性，将预测对象从广东地区30大汽车品牌扩展到全国42 个地区的30大汽车品牌以及全国30大汽车品牌进行扩展预测，以期达到能够真正指导实践的目的。

2   模型设计（Model design）

2.1   组合预测模型的原型

组合预测最早可追溯到1969 年BATES和GRANGER[5]提出的将单个预测组合成复合预测的原理，组合模型凭借可以有效去除滞后变量和非平稳性对预测的干扰[6]、在单项预测结果存在有偏性的情况下通过组合能产生具有无偏性的预测结果[7]等优势得到了研究学者的广泛应用，尤其是机器学习预测算法的引入，对通过识别长时间序列数据自身具有的规律性特征进而提升预测精度具有显著效果。组合预测模型如下：

假设选取种预测模型（，），每个模型在预测过程中均能够依据误差产生依据时间序列而变动的权重，则变权重组合预测模型可表示为：

式中，为随机噪音。

2.2   单项预测模型的选择

预测模型种类繁多且各有优劣势，从统计学层面来看，可分为回归问题和分类问题两大类。而在机器学习层面，可分为线性模型、树型模型和神经网络模型，例如，谢如贤等[8]（1992）使用ARMA、季节变量回归模型、指数自回归模型组成变权重组合模型对社会商品零售总额进行了预测，将平均误差（ME）降到了0.10;王永刚等[9]（2013）以灰色Verhulst模型、Brown指数平滑模型及非线性幂函数回归模型为单项模型，构建航空运输事故征候的最优变权组合预测模型，组合预测模型的平均绝对百分比误差（MAPE）为0.02323;朱周帆等[10]（2020）将SVM、RF、XGBoost与ARIMA模型相组合应用于汽车市场预测，平均绝对百分比误差（MAPE）为0.0297。通过对现有研究成果的归纳总结，本文选择的纳入组合模型的预测算法需要重点考虑能够处理季节性、趋势性、节假日等特征的模型，因此，初选模型包括ARIMA、HotWinters、Prophet、LightGBM、XGBoost、GM（1，1）。

2.3   权重设计与动态计算

预测效果的评估方法有绝对偏差、均方误差、均方根误差、平均绝对相对误差、平均绝对误差等，而权重的确定方法有等权重法、最小方差法、误差倒数法、优势矩阵法、权重收缩法等。在预测效果评价方面，本文选择绝对偏差法

（）作为评价准则;在权重方法选择方面，考虑到预测数据收到季节性、节假日等因素的影响，各预测算法对预测对象的预测结果存在动态误差[11]，权重同样需要考虑实时、动态的特征，所以本文使用熵值法[12]计算组合预测模型的参数。熵值法的基本原理是：假设有 个评价对象（各预测算法），有 个评价指标（各品牌预测误差），视计算结果情况将其归一化后转变为标准化数据，则其第 个指标的熵的计算公式为：

式中，为权数，为第项指标下第年占该指标的比重。将式（2）代入式（1）即得到基于熵值法的组合预测模型。

3   实例研究（Case study）

3.1   数据特征认知

本文研究使用的销量数据以月为单位，数据对象是汽车30大品牌的新车销量数据，数据范围包括全国销售数据和42 个主要地区的销售数据，选择2017 年1 月至2020 年9 月作为测试集，选择2020 年10 月至2021 年3 月数据作为验证集。因此，从数据的时间跨度来看，数据内涵既包括各品牌的销售行为等微观特征，又包括各地区经济发展、市场推广等宏观特征，这无疑都加大了预测难度。

（1）平稳性检验

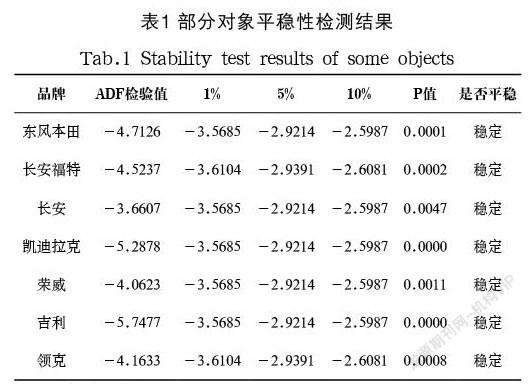
为进一步确定数据集的特征，本文使用ADF进行平稳性检验。平稳性是选择预测模型的先决条件，对于平稳型数据可使用AR、MA、ARMA等方式直接建模，而对于非平稳型数据则需要通过取对数、差分等方法处理后使用ARIMA进行建模。对平稳性的检验分为依据时序图和自相关图进行判断的图检验法以及构造检验统计量的假设检验法，前者主要依据研究者的经验以主观方式判断，后者可通过单位根检验法进行客观判别，因此，本文采取ADF方法进行检验。从如表1所示的检测结果表可以看出，30大品牌中不平稳对象占大多数，仅有7 个品牌（东风本田、长安福特、长安、凯迪拉克、荣威、吉利、领克）在数据期内平稳，因此，在模型选择中，ARMA、ARIMA应包含在选择对象之内。

（2）季节性判定

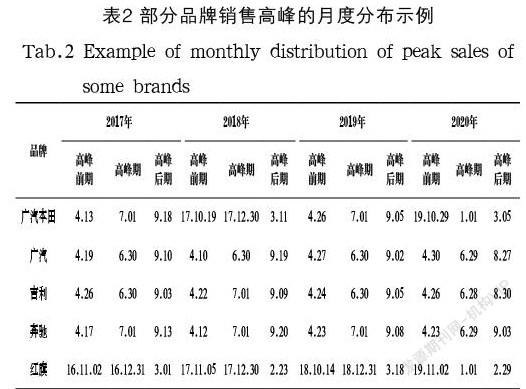
长期趋势、循环波动、季节性变化、随机波动是数据序列波动的四大类因素，因此，对季节性因素进行识别是提升预测精度的一个有效手段。本文使用圆形分布法结合集中度进行是否存在季节性以及集中月份的识别，该方法通过三角函数变换使得原始数据成为线性数据，进而识别季节分布特征。圆形分布法先将12 个月变换成360 度，1 年按365.2563 天计算，1 天相当于0.9856 度（360/365.2563），以1 月1 日零时为起点，以每个月月中值作为组中值折算为度，如：1 月份31 天，組中值为15.5 天，转换角度为15.2769 度;2 月份28 天，组中值为45（31+28/2） 天，转换角度为44.3524 度;其他以此类推。通过公式计算圆形分布的值、平均角和角标准差。由平均角和角标准差推算该对象的集中时间和增长高峰期，由于圆形分布法对数据格式的要求必须是整年数据，因此，选取2017 年、2018 年、2019 年、2020 年作为研究数据，并选取0.5作为标准差系数，经计算可得广东地区2017—2020年度30大品牌销售高峰的月度，如表2所示。

通过以上计算结果可以看出，各个品牌在研究期间内的季节性呈现出多样化的特征，各品牌差异化程度较高，例如广汽本田的销售高峰期分别是6 月底7 月初和12 月底1 月初，红旗品牌的销售高峰期则是12 月底1 月初，而奔驰品牌的销售高峰期则是6 月底7 月初。同时可以看出，广汽、吉利品牌的销售高峰近4 年均在6 月底7 月初。由此可见，各个品牌的季节性规律并不统一，基于此种数据特征，特将HotWinters、Prophet、LightGBM列入选择范围。

3.2   单项模型选择

通过对每个算法的预测进行实验，根据预测误差进一步淘汰了中位数误差较大的ARIMA、GM（1，1）、XGBoost模型，最终选取了HotWinters、Prophet、LightGBM三个模型，考虑到能够满足数据特征的预测算法相对较少，本文结合数据特征，基于Musgrave和Henderson系数单独设计了算法进行预测（下文简称Musgrave方法）。

针对本文研究的数据特征，本文使用Musgrave非对称滤子和Henderson滤子思想构建基于数据对称分布特征的预测[13]。在X-11中，使用Henderson移动平均可以从季节调整后序列中提取趋势这一成分，在应用项中心化移动平均时，由于结构限制，得不到序列最初项和最后项的平滑估计值，这容易给预测带来困扰，因为通常序列中最重要的点就是最末的那个点，因此在实际应用中需要采用非中心化移动平均来估计这些值。Musgrave的思路就是构建这样的非对称移动平均，能使得未来对估计值做出的修正达到最小。其基本原理是：

3.3   组合预测策略

（1）算法匹配策略

通过前期预测实验发现，不同的算法对同一品牌的预测能力、同一算法对不同品牌的预测能力均存在显著差异，在实际工作中预测中位数误差在6%以内具有较高的使用价值，因此本文将误差6%作为评价算法优劣的边界，而预测中位数误差在6%—10%具有一般的使用价值，因此，本文分别以6%、10%作为各算法匹配的阈值，具体匹配策略如下：

第一，对于在期预测累计双误差（均值和中位数）均低于6%的算法直接用于预测第期;如果对于多个算法都在6%以内的，则根据此算法在该品牌的预测误差权重，使用动态变权组合预测策略计算期综合预测值。

第二，对某品牌的中位数误差为的品牌的算法，使用组合算法进行预测，其中：①如果某个机构的某个品牌上有多个算法，中位数误差均在，则根据权重进行“动态组合预测”。②如果某个机构的某个品牌上只有一个算法，中位数误差均在，则使用该算法进行预测。

第三，对于某品牌的中位数大于0.1，选取各算法预测中位数误差较低的算法进行预测。

（2）预测维度选取策略

动态变权组合预测策略能否在实践中发挥关键作用取决于两个因素，其一是在满足数据特征多样性前提下带来的预测结果的准确性;其二是在一套匹配策略下能够满足不同类别预测场景的多样性。因此，本文并未从单一汽车品牌销量开始预测，而是考虑到以应用为核心目标，在明确数据时间的前提下从不同的维度采取如下策略：第一，在单地区多品牌维度方面，选取广东地区30大汽车品牌进行预测;第二，在多品牌维度方面，选取30大汽车品牌各自的全国销量进行预测;第三，在多地区多品牌维度方面，选取全国42 个主要地区的30大汽车品牌销量进行预测。之所以从这三个维度进行预测研究，其核心目的是在预测精度的前提下评估动态变权组合策略在多场景下的综合适用性，而本文的效果评估也从这三个维度展开。

3.4   预测效果评估

模型评估标准是对预测效果的直接决定影响因素，本文在评估方法方面考虑到预测对象数量较多，因此选择“误差中位数”作为标准。而在实践中，决策者经常需要对一段时间的销量进行跨期预测，因此本文选择2020 年10 月起至2021 年3 月累计6 个月销量进行预测测试，而各算法在这6 期的表现也将作为最终效果评价的标准。基于前述的假设，现将动态变权组合预测模型的预测效果总结和分析如下：

（1）以广东为例的单地区多品牌維度预测效果评价

在实践中，对单地区的汽车品牌销量进行预测可以有效指导分/子公司层面的经营行为，本文通过使用动态变权组合预测策略对广东地区30大品牌2020 年10 月至2021 年3 月销量进行预测，从动态变权组合预测策略所体现的误差中位数可以看出，动态变权组合预测模型的误差中位数为7.50%，明显低于其他单一预测模型，如表3所示。

（2）以全国为预测对象的多品牌维度预测效果评价

为进一步验证动态变权组合预测模型对宏观方面的适用性，本文继续对“全国30大品牌”进行预测，经过对预测结果统计分析发现，预测误差中位数为6.11%，依然低于其他预测模型，如表4所示。

（3）在多地区为预测对象的多品牌维度预测效果评价

为进一步体现动态变权组合预测的能力，本文将预测对象进一步拓展到“42地区30大品牌”。经统计分析发现，动态变权组合预测模型误差中位数为9.61%，预测效果依然比较优秀，但相比于前两类预测对象，误差中位数明显增加不少，如表5所示。对原始数据的研究表明，这主要是由于预测对象和数据维度增加了数据复杂度，进而加大了预测难度。

4   结论（Conclusion）

本文提出了一种动态变权组合的预测策略，综合来看，本策略除了能够显著提升预测效果外，更能扩大实践中的预测业务场景，可以进一步增强为决策者提供辅助决策的能力。本文虽有创新，但也存在以下不足，综合总结如下：

（1）预测对象数据特征的变化是决定动态变权的依据。实践表明，对预测对象数据特征的认知至关重要，引起数据特征变化的因素多种多样，既有行业因素，又有企业因素，还有国家和地区的政策因素，而这些都需要进行通盘考虑。更重要的是，针对每个因素导致的误差都要找到相应的预测解决方案，最终形成与预测算法、权重算法并重的数据认知算法模块。

（2）如何将权重实现智能计算需要进一步研究。本文在预测算法中使用了基于权重的动态匹配策略，因为权重在不同时间同样是一个变化的随机变量，所以在确定权重方法时，有必要实时考虑它的不确定性，除了本文使用的熵值法，权重的计算依然有综合评价法、Topsis法、方差倒数法等多种方法，如何通过方差、变异系数等更详细地评估各算法在预测过程中的稳定性，对权重的计算采用动态匹配模式非常值得进一步研究。

参考文献（References）

[1] 刘吉华，张梦迪，彭红霞，等.基于卷积神经网络的汽车销量预测模型[J].计算机科学，2021，48（6A）：178-189.

[2] 王炼，宁一鉴，贾建民.基于网络搜索的销量与市场份额预测：来自中国汽车市场的证据[J].管理工程学报，2015，29（4）：56-64.

[3] 刘吉华，张梦迪.基于百度指数的大众汽车销量预测研究[J].统计与管理，2020，35（279）：25-33.

[4] 王守中，崔东佳，彭赓.基于Web搜索数据的宝马汽车销量预测研究[J].经济师，2013（12）：24-26，28.

[5] BATES J M， GRANGER C. The combination of forecasts[J]. Journal of the Operational Research Society， 1969， 20（4）：451-468.

[6] HOLDEN K， PEEL D A. An empirical investigation of combinations of economic forecasts[J]. Journal of Forecasting， 2010， 5（4）：15-18.

[7] COULSON N E， ROBINS R P. Forecast combination in a dynamic setting [J]. Journal of Forecasting， 2010， 12（1）：63-67.

[8] 谢如贤，成盛超，吴健中.变权重组合预测模型的建立与应用[J].预测，1992，11（4）：64-67.

[9] 王永刚，郑红运.基于最优变权组合模型的航空运输事故征候预测[J].中国安全科学学报，2013，23（4）：26-31.

[10] 朱周帆，郝鸿，张立文.基于机器学习与时间序列组合模型的中国汽车市场预测[J].统计与决策，2020，36（548）：179-182.

[11] 凌立文，张大斌.组合预测模型构建方法及其应用研究综述[J].统计与决策，2019（01）：20-25.

[12] 狄淼，王明剛.基于熵权组合模型的风电功率预测[J].科学技术与工程，2012，20（29）：7713-7718.

[13] 中国人民银行调查统计司.时间序列X-12-ARIMA季节调整——原理与方法[M].北京：中国金融出版社，2006：76-85.

作者简介：

董志学（1980-），男，博士，算法工程师.研究领域：统计学，数学.

宫   越（1987-），女，硕士，算法工程师.研究领域：数据挖掘.

胡   勇（1973-），男，硕士，算法工程师.研究领域：机器学习.

甘孟壮（1986-），男，硕士，软件工程师.研究领域：自然语言处理，机器学习.