预测选择教与学优化算法的研究及应用

马云鹏 刘诗琳 董文菊 谢思琪 王子妍 吕定联

摘  要：教与学优化算法受教学现象的启发而提出，具有收敛速度快和模型参数少的优势。为了提高算法的收敛精度和全局搜索能力，提出预测选择教与学优化算法。首先，采用反向学习机制初始化种群个体位置，保持种群多样性。然后，在“教阶段”设置惯性权值和加速系数，提高算法的运算速度和解的质量。最后，在“学阶段”并行引入三种种群个体预测机制，选择最佳适应度值的个体进行下一次的寻优，提高算法全局搜索能力。通过基准数学函数测试得到的实验结果表明：改进算法的收敛精度和解的质量优于原始教与学优化算法。

关键词：教与学优化算法;预测选择;反向学习机制;收敛精度

中图分类号：TP181     文献标识码：A

Abstract： Teaching-learning-based Optimization （TLBO） algorithm with fast convergence speed and less parameter， is proposed based on teaching-learning practice. In order to improve convergence accuracy and global search ability of the algorithm， a Prediction-selection Teaching-learning-based Optimization （PSTLBO） algorithm is proposed. First of all， reverse learning mechanism is used to initialize the position of population individuals and to maintain population diversity. Then， inertia weight and accelerating factor are set in teaching phase to improve calculation speed and solution quality. Finally， in learning phase， three kinds of population prediction mechanisms are introduced in parallel and the individual with the best fitness value is selected for the next optimization， which improves the global search ability of the algorithm. Through benchmark mathematical function test， the experimental results show that convergence accuracy and solution quality the improved algorithm are better than the original teaching-learning optimization algorithm.

Keywords： teaching-learning-based optimization algorithm; predictive selection; reverse learning mechanism;                      convergence accuracy

1   引言（Introduction）

基于真实班级教学现象的启发，RAO教授于2010年提出教与学优化（Teaching-learning-based optimization， TLBO）算法，其属于启发式群智能优化算法[1]。TLBO算法计算规则简单，运行参数较少，全局搜索能力良好，近年来引起国内外研究学者的广泛关注[2-6]。但是，TLBO算法仍然存在一些缺点，如其善于解决单峰函数问题，对于多峰函数易陷入局部最优点;在算法运行后期，种群个体靠近最优解，导致种群多样性丢失;收敛精度和收敛速度还可进一步提升等。

针对上述不足，文献[7]运用动态分组机制来提高TLBO算法的全局搜索能力;文献[8]引入局部学习机制和自学习机制来提高TLBO算法的搜索能力;文献[9]应用反向学习机制和类反向学习机制提高TLBO算法的收敛速度和解的质量;文献[10]设计惯性权值和加速权值来提高TLBO算法的收敛速度和解的质量;文献[11]通过对教师个数的设置和教学系数的改进，并引入自学习机制来提高TLBO算法的性能。

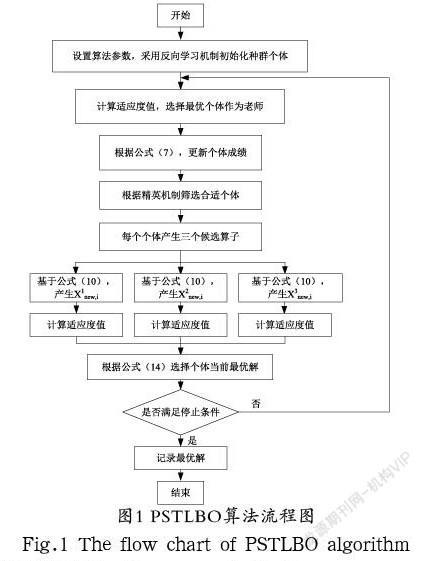
为了进一步增强TLBO算法的收敛精度和全局搜索能力，本文提出一种预测选择教与学优化算法（Prediction-Selection Teaching-Learning-Based Optimization， PSTLBO）。该算法引入三种改进机制：（1）应用反向学习机制初始化种群个体位置，保持种群多样性，增強探索能力;（2）在“教阶段”引入惯性权值和加速系数，提高算法的运行速度;（3）在“学阶段”，引入预测选择机制，即预先设计三种种群个体位置更新机制，更新后选择适应度值最优个体作为下一次迭代的解，可以提高全局搜索能力。为了验证改进算法的性能，采用十个基准数学函数进行测试，同时与人工蜂群算法[12]、万有引力算法[13]和原始教与学优化算法做对比，实验结果表明，预测选择教与学优化算法具有良好的收敛精度和全局搜索能力等性能。

2  教与学优化算法（Teaching-learning-based optimization algorithm）

TLBO算法的思想是：选择学习成绩最好的个体作为老师，老师通过“教”来提高班级的平均成绩;学生既向老师获得知识，又与其他人进行交流，最终提高自身成绩。因此，TLBO包括两个阶段：“教阶段”和“学阶段”。该算法的计算步骤概括如下：

（1）定义优化问题，初始化算法参数、种群规模和终止条件等。

（2）“教阶段”。种群个体位置更新公式如式（1）—式（3）所示。

上述公式中，为教学系数，启发步长，取1或2;为随机数，;为平均成绩;为第个个体的适应度值。

3   预测选择教与学优化算法（Prediction-selection TLBO algorithm）

在原始TLBO算法的基础上，本部分设计预测选择教与学优化算法。首先，对种群个体初始化方式进行改进，运用反向学习机制初始化种群个体位置;然后，在“教阶段”引入两种权值，即惯性权值和加速系数;最后，在“学阶段”提出预测选择机制更新种群个体位置。该算法的具体实现过程如下所述。

3.1   反向学习机制初始化个体

假设在维搜索空间中存在一点，

在初始化种群个体时，采用反向学习机制在解空间范围内将产生 个个体，从中选择 个最优个体作为初始种群个体。通過反向学习机制对个体初始化，可以保持种群多样性，有利于提高全局搜索能力，更容易接近最优解。

3.2   教阶段

其中，是惯性权值，控制着的影响;是加速系数，提高“教阶段”的搜索速度;是第 个学生的适应度值;是第一次迭代中最大的适应度值;是当前的迭代次数。

3.3   学阶段

在“学阶段”，引入三种不同形式的种群个体更新机制，称之为预测选择机制，如式（10）所示。由式（10）可知，每一个更新算子与当前最优解、个体自身信息或随机选择的某个个体信息有关。该机制预先产生三个个体

4   性能测试（Performance testing）

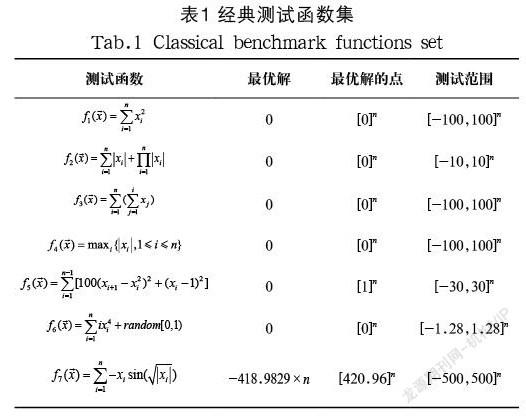
为了验证PSTLBO算法的性能，应用10 个基准数学函数测试算法的收敛精度和搜索速度，测试函数记录于表1。此外，将预测选择教与学优化算法（PSTLBO）与人工蜂群算法（ABC）、万有引力搜索算法（GSA）、原始教与学算法（TLBO）进行比较，各算法的参数设置如表2所示，实验结果记录于表3。

由表1可知，f1-f6为单峰高维函数，f7-f10为多峰高维函数，同时给出函数的最优点和自变量的取值范围。表2给出四种智能优化算法的参数设置，每个仿真运行30 次，每一种算法单次运行迭代1，000 次，运行结果记录于表3，最优值加粗显示。如表3所示，每一个基准函数的维数依次设置为10 维、30 维、50 维，从运行结果来看，PSTLBO算法能够找到在不同维度下的最优值或理论最优值，说明PSTLBO具有良好的收敛精度。为了更直观地显示实验结果，分别给出在10 维和在50 维时的仿真图，如图2和图3所示。由图2和图3可知，PSTLBO具有收敛速度快和收敛精度高的性能。

5   结论（Conclusion）

为了进一步提高教与学优化算法的收敛精度和解的质量，分别对种群个体初始化方式，以及“教阶段”和“学阶段”的种群个体位置更新方式进行修正。运用反向学习机制初始化种群个体，使之更容易接近最优解和增加种群多样性。预测选择更新算子的引入，可有效平衡算法的探索能力和开发能力。通过与其他算法在基准测试函数上的性能对比，说明PSTLBO具有良好的收敛速度和收敛精度，解的质量得到提高。

今后，PSTLBO算法的性能将进一步提高，并应用于工程优化问题中。同时，基于PSTLBO算法，设计多目标PSTLBO算法。

参考文献（References）

[1] RAO R V， SAVSANI V J， VAKHARIA D P. Teaching–learning-based optimization： A novel method for constrained mechanical design optimization problems[J]. Computer-Aided Design， 2011， 43（3）：303-315.

[2] KUMAR Y， SINGH P K. A chaotic teaching learning based optimization algorithm for clustering problems[J]. Applied Intelligence， 2019， 49（3）：1036-1062.

[3] 于坤杰，王昕，王振雷.基于反馈的精英教学优化算法[J].自动化学报，2014，40（9）：1976-1983.

[4] MA Y， ZHANG X， SONG J， et al. A modified teaching-learning-based optimization algorithm for solving optimization problem[J]. Knowledge-Based Systems， 2021， 212：106599.

[5] LI S， GONG W， YAN X， et al. Parameter extraction of photovoltaic models using an improved teaching-learning-based optimization[J]. Energy Conversion and Management， 2019， 186：293-305.

[6] 拓守恒，邓方安，雍龙泉.改进教与学优化算法的LQR控制器优化设计[J].智能系统学报，2014 （5）：602-607.

[7] ZOU F， WANG L， HEI X， et al. Teaching–learning-based optimization with dynamic group strategy for global optimization[J]. Information Sciences， 2014， 273：112-131.

[8] CHEN D， LU R， ZOU F， et al. Teaching-learning-based optimization with variable-population scheme and its application for ANN and global optimization[J]. Neurocomputing， 2016， 173（P3）：1096-1111.

[9] SULTANA S， ROY P K. Multi-objective quasi-oppositional teaching learning based optimization for optimal location of distributed generator in radial distribution systems[J]. International Journal of Electrical Power and Energy Systems， 2014， 63（12）：534-545.

[10] LI G， NIU P， ZHANG W， et al. Model NOx emissions by least squares support vector machine with tuning based on ameliorated teaching-learning-based optimization[J]. Chemometrics and Intelligent Laboratory Systems， 2013， 126（8）：11-20.

[11] RAO R V， PATEL V. Multi-objective optimization of two stage thermoelectric cooler using a modified teaching-learning-based optimization algorithm[J]. Engineering Applications of Artificial Intelligence， 2013， 26（1）：430-445.

[12] KARABOGA D， GORKEMLI B. A quick artificial bee colony （qABC） algorithm and its performance on optimization problems[J]. Applied Soft Computing， 2014， 23：227-238.

[13] YAZDANI S， NEZAMABADI P H， KAMYAB S. A gravitational search algorithm for multimodal optimization[J]. Swarm and Evolutionary Computation， 2014， 14：1-14.

作者簡介：

马云鹏（1989-），男，博士，讲师.研究领域：机器学习，仿生智能计算.本文通讯作者.

刘诗琳（2000-），女，本科生.研究领域：仿生智能计算.

董文菊（2001-），女，本科生.研究领域：仿生智能计算.

谢思琪（1999-），女，本科生.研究领域：神经网络.

王子妍（2001-），女，本科生.研究领域：特征提取.

吕定联（2001-），女，本科生.研究领域：数据挖掘.