特高压直流输电线路离子流场快速稳定计算方法

修连成，杜志叶，岳国华，何靖萱，蔡泓威，易凡

(1.武汉大学电气与自动化学院，武汉430072；2.空军预警学院雷达士官学校，武汉430345)

0 引言

近年来，随着我国电能需求的不断增加，特高压直流输电技术在电力系统中得到广泛运用[1-3]。当特高压直流输电线路的导线和金具表面电场强度超过起晕电场强度时，其表面会发生电晕[4-7]，导线和金具周围产生了正、负电荷。因为直流输电线路导线极性不变，电荷受到电场力的作用向空间中扩散，与标称电场作用形成了合成电场，提高了地面电场强度[8-10]。由于输电电压等级的不断提高，线路附近的电磁环境问题更加严重。因此，特高压直流输电线路下方的离子流场研究具有非常重要的意义。

解析求解是一种可以精确计算离子流场的方法，其原理是根据场域及其内部物理量分布对称特性，从而获得与边界条件对应的唯一解[11]。但是，该方法只能求解相对简单的结构，如同轴圆柱模型、平行板模型等。为了解决复杂模型离子流场求解问题，文献[12-13]基于Deutsch假设提出了一种离子流场计算方法，实现了复杂模型的离子流场快速求解。然而，该假设认为空间电荷只会影响电场数值，而不会改变电场方向，这与实际情况有所区别。而且在含有风速影响时，采用Deutsch假设的离子流场求解精度较低。文献[14]提出一种利用Kaptzov假设求解离子流场的有限元方法。针对不同结构的直流输电线路问题，文献[15-18]利用基于Kaptzov假设的有限元法对其离子流场进行了求解和分析。文献[19-20]通过有限元法计算了单极和双极直流输电线路的离子流场。有限元法求解过程主要分为两个部分：首先，通过假设的初始电荷密度求解泊松方程，实现获取空间电场信息。随后，利用空间电场和电流连续性方程计算空间电荷密度。将上述两部分反复迭代即可获得地面合成电场和离子流场分布。但是该方法在求解复杂模型时经常会发生迭代过程不收敛的情况。

为了快速准确地求解特高压直流线路离子流场，文献[21]提出了一种上流有限元法来求解直流线路的离子流场。上流有限元法的原理是搜寻和确定上流有限单元，从而实现由电荷源点向外扩散求解的目标。基于上流有限元法和Kaptzov假设对输电线路的合成电场和离子流密度进行了求解[22-23]。文献[24]基于上流有限元法提出了一种减少剖分网格数量的方法。该方法将二维上流有限元法求解的离子流场当作三维求解时输电导线的求解边界。但是上述文献对初始导体表面电荷敏感度较高，迭代过程容易无法收敛。文献[25]提出了一种偏差估算法来计算初始导线表面电荷密度。但是该方法的迭代步数较多，迭代计算时间较长。

本文通过基于牛顿-拉夫逊的上流有限元法求解特高压直流线路下方的地面合成电场与离子流场。该方法不仅无需调整和优化算法参数，还提高了收敛能力。该算法应用简单，鲁棒性强，可求解复杂情况下的地面合成电场和离子流密度。

1 离子流场模型

特高压直流输电线路离子流场模型中的正、负电荷主要受到了风力和电场力的影响。因此，离子流场的控制方程可以表示为：

(1)

j+=ρ+(k+E+W)

(2)

j-=ρ-(-k-E+W)

(3)

(4)

(5)

(6)

式中：φ为电位，V；ρ+、ρ-分别为正、负电荷密度，C/m3；ε0为空气介电常数；j+、j-分别为正、负离子流密度，A/m2；k+、k-分别为正、负离子迁移率，m2/Vs；E为电场强度，V/m；W为风速，m/s；Rn为复合系数。

将式(1)—(6)代入式(4)和式(5)，可得：

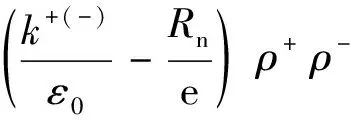
(7)

式中V+(-)为正、负离子的迁移速度。

特高压直流输电线路下方的离子流场求解属于强非线性问题，很难实现直接准确求解，因此需要简化离子流场模型[26]。同时，假设条件应对地面离子流场计算结果影响较小，即

1)忽略特高压直流输电导线的电晕层厚度；

2)电晕已到达稳态，不考虑暂态过程；

3)导线表面场强满足Kaptzov假设；

4)正、负离子的迁移率、复合系数和风速与电场无关，即设置为恒定常数。

2 基于牛顿-拉夫逊的离子流场求解算法

求解电流连续性方程是离子流场计算的重要环节。因此，本文通过上流有限元法求解电流连续性方程。上流有限元法的基本原理是通过三角单元的两个已知电荷密度节点去计算另一未知电荷密度节点[5,7]。空间正电荷密度可描述为：

(8)

式中：下标i,j,m分别代表不同节点；bijm和cijm均为三角形单元的节点坐标函数；SΔ为三角形单元面积。

由式(7)—(8)可得特高压直流输电线路的正电荷密度。正、负电荷密度求解思路一致。因此，节点i处的正、负电荷密度为：

(9)

式中：

(10)

(11)

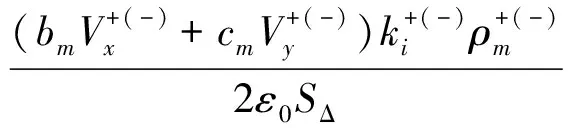
(12)

式(9)的求解结果实现了从源点电荷发出并扩散到整个场域，与实际情况相符，保证了电流连续方程的收敛性。

在迭代求解过程中，导线表面电场场强变化较大时会导致更新的导体表面电荷密度发生大幅度振荡，进而使迭代过程不收敛。同时，导线表面电荷密度的初值设置对计算泊松方程和电流连续性方程时的收敛性影响较大。当电荷密度的初值选择不恰当时，迭代过程容易发生振荡不收敛的情况。为此，本文提出了一种基于牛顿-拉夫逊的迭代收敛算法，具体证明如下。

假设迭代电荷密度方程属于单变量非线性方程，即可得：

f(ρi)=0

(13)

将式(13)改写成式(14)。

f[ρi(k-1)+Δρi(k-1)]=0

(14)

式中：ρi(k-1)为节点i在第k-1次迭代时的电荷密度；ρi(k-1)和Δρi(k-1)分别为迭代电荷密度方程的近似解和真解误差。

根据泰勒公式原理，式(14)可改写为：

f[ρi(k-1)+Δρi(k-1)]=

f[ρi(k-1)]+f′[ρi(k-1)]Δρi(k-1)+

(15)

迭代电荷密度方程的真解误差Δρi(k-1)相对较小，因此可以忽略其二阶以上的高次项，即：

f[ρi(k-1)+Δρi(k-1)]=

f[ρi(k-1)]+f′[ρi(k-1)]Δρi(k-1)

(16)

根据式(14)和式(16)可知，真解误差Δρi(k-1)的修正解可表示为：

ρi(k)=ρi(k-1)+Δρi(k-1)

=ρi(k-1)-f(k-1)/f′(k-1)

(17)

根据式(17)可知，改进算法依据迭代过程的前2步导线表面电荷密度来求解新的电荷密度。该算法在导线表面场强与起晕场强相差较远(较近)时，电荷密度更新较快(较慢)，保证了算法的快速稳定收敛。因此，本算法对导体表面电荷密度的初始值不敏感。具体控制过程如下。

ρi(k)=ρi(k-1)+Δρi(k-1)=

(18)

式中：Emaxk-1、Emaxk-2分别为第k-1、k-2次迭代时导线表面的最大电场强度；E0为导线表面起晕场强。

式(18)解决了导体表面电荷密度快速收敛到真值附近问题。但是当计算空间电荷密度时，前后两次迭代的空间电荷密度大幅度变化，可能会导致计算不收敛。因此，本文引入了迭代变化系数到空间电荷密度更新中，确保迭代稳定收敛。空间电荷密度可以表示为：

ρis(k)=(1-v)ρis(k-1)+ρisc(k)v

(19)

式中：ρis(k)、ρis(k-1)分别为上一步迭代过程中的空间电荷密度；ρisc(k)为当前迭代步中根据上一步有限元法计算得到的空间电荷密度；ν为迭代变化系数。

综述所述，在迭代过程前期，输电导线表面的电荷密度距离实际电荷密度相差较远。因此，本算法加大了调整电荷量，确保迭代过程快速进行，提高迭代过程计算效率，使得导线表面电场强度可以快速接近起晕场强。在迭代过程后期，本算法减少了更新的电荷量，使得本算法可以稳定收敛。离子流场的收敛条件为：

(20)

(21)

式中：δE、δρ分别为导线表面的电场强度和电荷密度相对误差；Emax为导线表面的最大电场强度。

当导线表面未发生电晕时，通过求解拉普拉斯方程获得空间电场分布。而求解离子流场主要分为四个步骤：通过空间电荷密度求解泊松方程得到空间电场分布信息；利用空间电场信息和上流有限元法求解电流连续性方程；判断是否满足Kaptzov假设和电荷密度结果稳定的收敛条件；如果不满足稳态收敛条件，则采用基于牛顿-拉夫逊的迭代收敛算法来修改电荷密度。将上述过程重复迭代到达收敛条件。离子流场求解的流程图如图1所示。

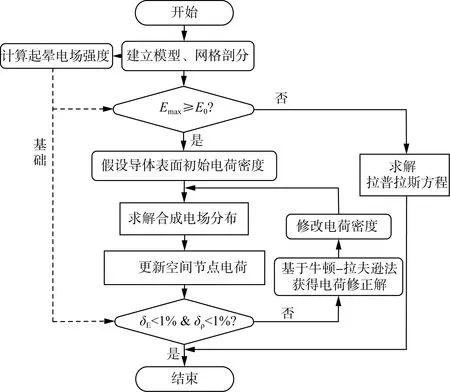
图1 离子流场计算流程图

3 算法验证

3.1 试验模型验证

通过单极直流试验线路模型来验证本文所提出的新型迭代收敛算法的正确性和有效性。该模型的直流导线施加电压为30 kV，导线半径为0.8 mm，直流导线高度为0.394 m，试验平台如图2所示。在导体模型下方放置场磨探头和威尔逊板，用于测量地面电场强度和离子流密度。图中左侧的高压发生器控制台用于控制导线电压等级。送风机用于控制试验风速。

图2 试验平台

参考国家标准GB/T 37543—2019中的评价依据对试验数据进行了统计。图3给出了不同风速下的本文算法与试验测量数据的对比结果。图3(a)和3(b)中的紫(深)色点和黄(浅)色点分别表示在风速为0 m/s和3 m/s时的测量结果。

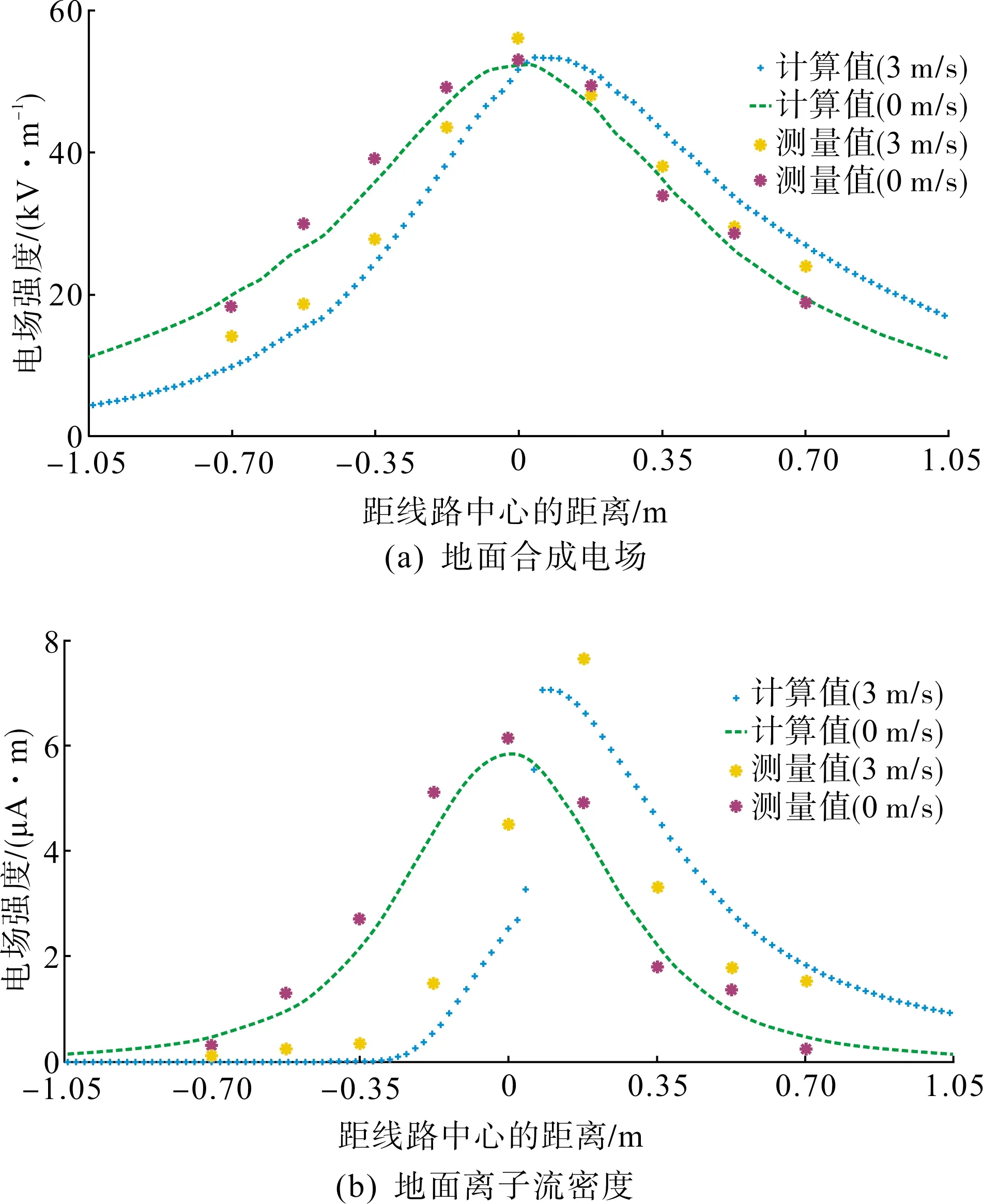
图3 计算和测量结果对比

根据图3(a)，本算法求解的地面合成电场结果与试验线路的测量结果相差较小。特别是在风速值为0 m/s时，计算值与测量值基本一致。本算法的离子流密度计算值与实际测量值对比如图3(b)所示。实际测量峰值下降速度比本文方法的计算值下降速度稍快。但计算值与实际测量值基本一致，证明了本算法的正确性。需要说明的是，风速对离子流密度和合成电场影响明显。电荷由逆风侧被吹至顺风侧，合成电场最大值位置也向顺风侧发生偏移。

3.2 算法收敛性与稳定性分析

本文利用云南—广东± 800 kV特高压直流输电线路模型来验证本算法的收敛性和稳定性。该线路导线数据详见参考文献[27]。当初始导线表面电荷不同时，本算法求解离子流场的迭代收敛结果如图4所示。图中导线表面初始电荷密度分别为1×10-8、5×10-8、1×10-7、1.5×10-7和2×10-7C/m3。显然，本算法在不同初始导线表面电荷密情况下都能够快速稳定收敛，且迭代步数都少于20步。

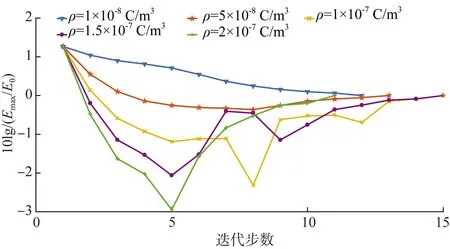
图4 收敛效果验证

当初始导线表面电荷为2×10-7C/m3时，将本文算法、收敛控制因子法以及传统方法进行了对比，如图5所示。传统方法对电荷敏感度较高，容易出现迭代振荡，从而导致计算无法收敛。迭代收敛控制因子法和本文算法都能够实现稳定的迭代收敛。

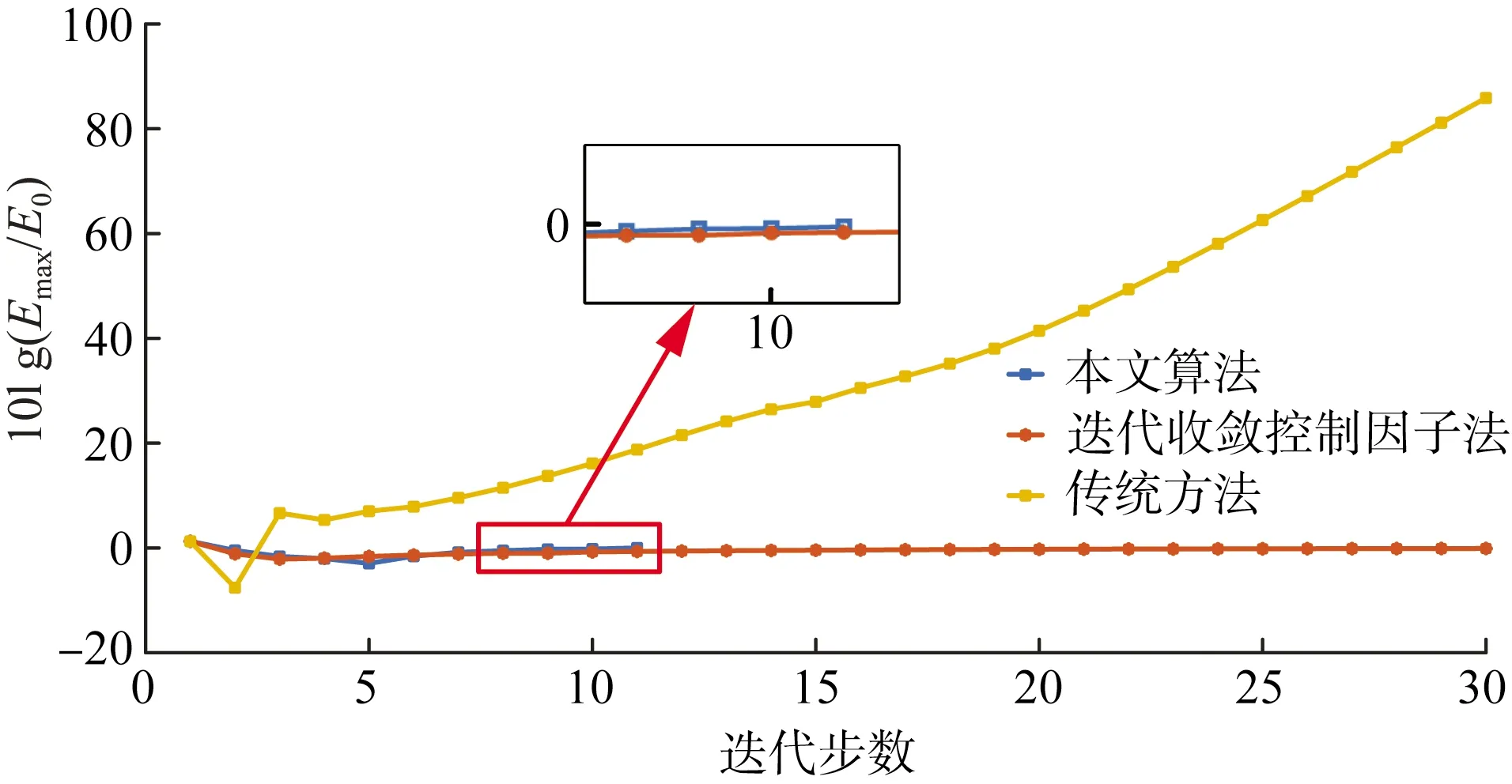
图5 不同方法收敛速度对比

迭代收敛控制因子法对初始导线表面电荷密度不敏感，但该方法需要设置控制因子，且控制因子值的大小与收敛性和计算速度直接相关。当控制因子较小时，迭代过程中的电荷密度变化不大，进而实现稳定收敛。但是，其迭代速度较慢，计算时间变长。当控制因子较大时，迭代收敛速度变快，然而导体表面电荷变化较大，可能导致无法收敛。由图5可知，迭代收敛控制因子法虽然能够较快速到达电荷真值附近，但是仍需要多次迭代才能达到收敛条件。而本文所提出的算法迭代速度较快，且无需复杂的算法参数调整与优化。特高压直流输电线路的导线表面电荷和表面电场强度变化情况如图6所示。

图6 导线表面电荷和表面电场强度变化曲线

本文算法在迭代过程初期的导线表面电荷密度变化程度较大，而迭代后期的电荷变化较小，使得本文算法可以快速稳定迭代收敛。迭代初期(3～10步)，导线附近合成电场强度变化剧烈，使得导体表面电荷变化率较大，从而实现快速地迭代到起晕场强附近。迭代后期，导线表面电荷变化率较小，确保离子流场迭代稳定收敛，防止在起晕场强附近发生振荡。因此，本文算法实现了快速稳定地计算特高压直流线路下方离子流场。

4 风速对±800 kV特高压直流输电线路离子流场影响分析

本文以± 800 kV特高压直流输电线路为例进行了地面离子流场求解，得到了地面合成场强和地面离子流密度在不同风速下的分布规律。具体线路参数和测量数据见参考文献[27]。图7和图8分别表示了不同风速时地面合成电场强度和离子流密度。

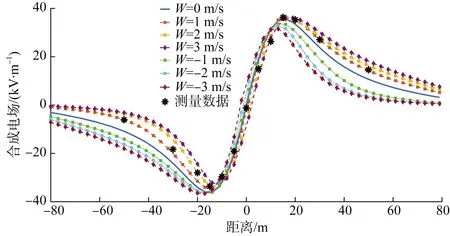
图7 地面合成场强求解结果

图8 地面离子流密度求解结果

图7—8中风向从左侧向右侧为正，风速从-3 m/s增加到3 m/s。当风速从-3 m/s增加时，合成场强和离子流密度的最大值位置逐渐向右侧移动，且其最大值先减小后增加。本文计算的合成电场和离子流密度与测量结果基本一致，验证了本算法的有效性和正确性。

随着风速向左增加，正极性导线下方地面合成场强和离子流密度逐渐增大，而负极性导线下方的离子流场有所减小。当风速值从0 m/s增加时，负极性下方的合成电场和离子流密度逐渐减小。这是由于负极性导线下方的空间电荷都被吹到了正极性导线下方，从而导致负极性导线下方的合成电场和离子流密度减小。当风速值为3 m/s时，最大合成场强为36.58 kV/m，且最大离子流密度为83.6 nA/m2。同时，对比于风速为0 m/s时的最大合成电场，其位置发生了约5 m的偏移。综上所述，随着风速向右(向左)增大，合成场强和离子流密度的分布曲线和最大值都逐渐向右(向左)移动，而且顺风侧导线的合成场强和离子流密度数值均会显著变大。

本文算法在不同风速情况下求解合成电场和离子流场时，迭代过程一般少于20步，相比于传统方法缩短了计算时间，且满足工程精度要求。同时，本文所提出算法不但对导体表面电荷密度初值选择不敏感，而且无须调整和优化算法参数，具有较好的鲁棒性。

5 结语

为了解决特高压输电线路离子流场计算的快速稳定收敛问题，本文基于牛顿-拉夫逊法提出了一种快速稳定求解离子流场算法。该算法在导线表面场强距离起晕电场强度相差较大(较小)时，电荷密度更新较多(较少)，从而实现了快速稳定收敛。通过对实验室模型线路的地面合成电场和离子流场计算，验证了本算法的有效性和正确性。同时，本文对±800 kV 特高压输电线路下方离子流场进行了求解，证实了该算法可以提高求解速度并保证收敛的稳定性。随着向右风速的增加，正极性导线下方的地面合成场强和离子流密度逐渐增大，而负极性导线下方的离子流场数值逐渐减小。该算法不但对导体表面电荷密度初值选择不敏感，而且无需调整算法参数，具有较好的鲁棒性。研究结论有助于快速准确计算特高压直流输电线路下方离子流场。