高压交流输电线路邻近城市高层建筑时的畸变电场计算

杨勃，徐禄文，刘彤

(1.国网重庆市电力公司电力科学研究院，重庆401123；2.电力系统及发电设备控制和仿真国家重点实验室(清华大学电机系)，北京100084)

0 引言

目前，对于交流高压输电线路附近存在建筑物时附近空间中畸变电场计算的研究，大多数选择的研究场景为线路附近存在单个低层建筑，这种场景适用于分析线路临近或穿越较为空旷的农村。随着架空线分布越来越密集，需要进一步考虑线路临近或穿越城市居民区中高层建筑群时电场的畸变情况。本文主要研究高层建筑附近高压交流输电线路的畸变电场。

由于ANSYS和COMSOL等商业软件的大量应用，已经有大量论文报道采用商业软件计算输电线路周围的工频电场。商业软件建模能力强，前处理和后处理的功能都很灵活。由于商业软件采用有限元法，其适用于有限边界的问题，而本文所计算的场域是无限大，需建立人工边界截断无限远域，这在实践中有一定的不方便性。

在计算方法方面高压交流输电线路电场计算并非新问题，目前常见计算方法包括基于微分方程求解的有限元法、有限差分法和基于求解的边界元方法、模拟电荷法和矩量法[1-10]。针对高压输电线路结构和计算区域为半无限大空间的特点，基于积分方程求解的数值计算方法得到了广泛的应用[11-13]。

从计算的场景来看，考虑高层建筑的影响，此时应采用三维模型进行分析和求解空间电场。从原理上讲，二维和三维模型在计算步骤上并无本质区别。但是，在数值实现上，三维模型的计算量远大于二维模型，从计算时间和计算精度两方面考虑，需要对三维问题进行一定的简化，从而获得计算精度和计算时间的折衷。综合以上因素，本文采用模拟电荷法与表面电荷法[14-15]结合的计算方案求解高层建筑物附近交流高压输电线路的畸变电场，分析高层建筑物对居民活动区工频电场分布的影响。

1 高层建筑附近高压交流输电线路畸变电场计算模型

根据导体的形状特点，本文采用模拟电荷法和表面电荷法相结合的计算模式。对于导线和地线采用模拟电荷法建立三维模型，即采用一系列线电荷单元等效替代导线表面的电荷；对于建筑物采用表面电荷法建立三维模型，将建筑物表面用三角形单元剖分。由于不考虑杆塔影响时电场的畸变更为严重，本文在计算中忽略杆塔的影响。

1.1 边值问题描述

高压交流输电线路附近存在建筑物时空间电场的属于准静态场，其满足边值问题如图1所示。输电线路在正常运行工况下，其空间电场强度是一个呈50 Hz变化的时变电磁场。由于场量变化缓慢，此时可采用计算静态电场的方法予以计算。

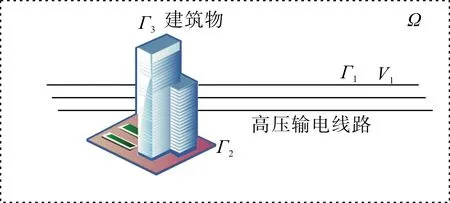
图1 计算场景示意图

在输电线下方建立直角坐标系，空间中任意点处的电位由三相输电线路共同作用产生，如设求解的变量为空间任意点处的电位φ(x,y,z)，此问题可以用式(1)所示方程组来描述，空间Ω中任意一点φ(x,y,z)满足Laplace方程。

(1)

式中：Γ1表示输电线路带电导体的表面；V1为带电导体在不同工况下的电压值；Γ2表示大地表面，其表面电位为参考电位，设为0；Γ3表示输电线路下方建筑物的表面，由于建筑物接地，其表面的电位与大地相同，其值为0。无穷远处电位为0是实际物理问题自然边界条件。

1.2 模拟电荷法与表面电荷法结合的计算方案

空间任意一点的电场强度是由边界上所有电荷作用的叠加产生的，电荷分布在导线表面、建筑物表面和大地表面。大地表面的电荷可通过镜像原理考虑。对于导线和建筑物，由于他们的外形特点不同，导线属于线状导体，建筑物属于块状导体，所以对于其表面的电荷需要用不同的方法描述。对于导线，可采用模拟电荷法对其进行建模，即将导线表面的电荷用线电荷等效替代。

对于建筑物，由于其属于块状导体，采用模拟电荷法难以精确模拟电荷的类型、放置位置、导体边界电位，同时对于不同的建筑物需要根据其外形重新选择和放置模拟电荷。本文采用表面电荷法可以直接对建筑物表面电荷进行剖分，从而可以充分考虑建筑物复杂的几何形状。

以导线的等效线电荷密度和建筑物表面电荷密度为未知量，线路表面或建筑物表面任意一点Pi处的电位φ(Pi)的表达式为：

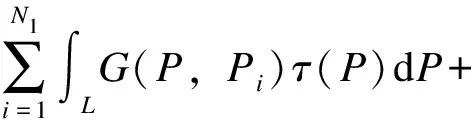
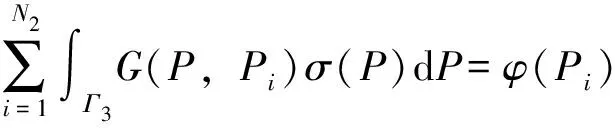
(2)

式中：N1为输电线路导线与地线的数量；L为输电线路导体的描述方程；N2为建筑物的数量，G3为表示建筑物的外表面；t(P)为线路导线与地线的等效线电荷密度；σ(P)为建筑物表面的等效面电荷的电荷密度；φ(Pi)为观察点Pi的电位，为已知量；P为表面电荷源点；Pi为观察点；G(P,Pi)为等效电荷或P和Pi之间的格林函数。

考虑大地的镜像作用时，G(P,Pi)可以表示为：

(3)

式中：ε0为空气的介电常数；r和r′分别为场点和原点的坐标，有：

(4)

(5)

为了将积分方程式(2)转化为一系列的代数方程，将导线的等效线电荷剖分成一系列的线电荷单元，同时将建筑物表面的电荷剖分成一系列三角形(也可以是四边形)面电荷单元，如图2所示。本文中这些单元上的电荷密度均设为常数。

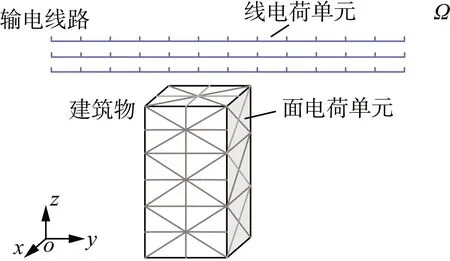
图2 线电荷单元与面电荷单元划分示意图

如图3所示，对第i个线电荷单元来说，其匹配点处的电位为Vi，以所有线电荷单元以及面电荷单元的电荷密度为未知量，可将Vi用式(6)表示。

图3 线电荷单元与面电荷单元示意图

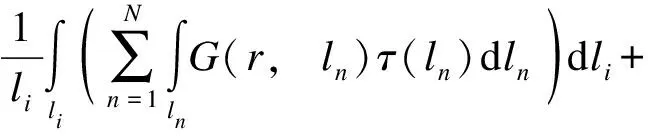
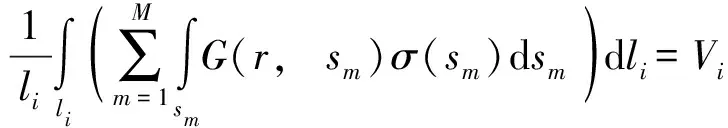
(6)

式中：N为线电荷单元的数量；M为面电荷单元的数量；ln和sm分别为第n段和第m段的广义坐标；τ(ln)为第n个线电荷单元ln的电荷密度；σ(sm)为第m个面电荷单元sm的电荷密度；li为第i个线电荷单元的长度；Vi为第i线电荷单元所对应导体段表面的平均电位；G(r,ln)和G(r,sm)分别为线段单元和面单元的格林函数。

对第j个面电荷单元来说，其匹配点处的电位为0，可用式(7)表示。

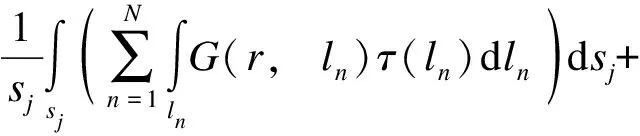
(7)

式中sj为第j个面电荷单元的面积。

需要指出的是，由于面电荷单元的匹配点就在单元本身，所以求解面电荷单元自身电荷对自身电位的贡献时，会出现积分奇异的问题，所以面电荷单元自身对自身的电位系数需要单独计算。以长和宽分别为a和b的矩形单元为例，若匹配点位于其几何中心，则自电位系数计算公式为[11]：

(8)

本文在计算三角形单元的自电位系数时，首先将其转化为面积相等的正方形，再按式(8)进行计算。

如果直接按式(6)将线单元的电荷密度作为未知量求解，此时形成的方程组是不对称的，这将增大矩阵系数的计算量。为了解决这一问题，将式(6)改写为式(9)。注意，式(9)中添加ln项和Sm项，这样电位系数归一化为与线电荷单元长度和面电荷单元面积均无关的系数，即此时的系数对于任意2个电荷单元是互易的，即所形成的系数矩阵是对称的。同理，对式(7)，按照处理式(6)的方法进行改写，形成新的方程如式(10)所示。

(9)

(10)

对式(9)和式(10)进行离散处理，形成一系列的代数方程，并将其写成式(11)的矩阵形式。

(11)

求解式(11)，可获得导线和建筑物表面的电荷，进一步可得到单元的电荷密度。根据这些电荷密度，可以获得空间任意场点处的电场强度。

2 高压交流输电线路邻近高层建筑时建筑物附近电场畸变研究

随着输电线路架设越来越密集，不可避免地会出现线路穿越城市居民区的情况，城市居民区建筑与农村建筑的区别是楼层高且以建筑群的形式出现，研究高层建筑群附近畸变电场的计算及电场分布规律可以对输电线路和城市小区的建造提供指导意义，也可对已经建成的小区的电磁环境进行评估，为后续的电磁环境改善提供具有参考价值的数据。

本节采用上节所述的模拟电荷法与表面电荷法耦合的计算方案，研究单个高层建筑附近的交流输电线路电场环境畸变情况。以500 kV交流单回输电线路和18 m×24 m×81 m的高层建筑物为研究对象。输电线路的参数见表1。研究场景的三视图如图4所示。本次研究选取的第1组为建筑物临近线路一侧的处于地面上方1.5 m水平面的3条平行于线路的采样线，3条采样线距离建筑物表面的距离分别为2 m、4 m和8 m，采样的长度均为36 m，为建筑物的宽长向两端各延长50%。采样线的位置如图4所示。

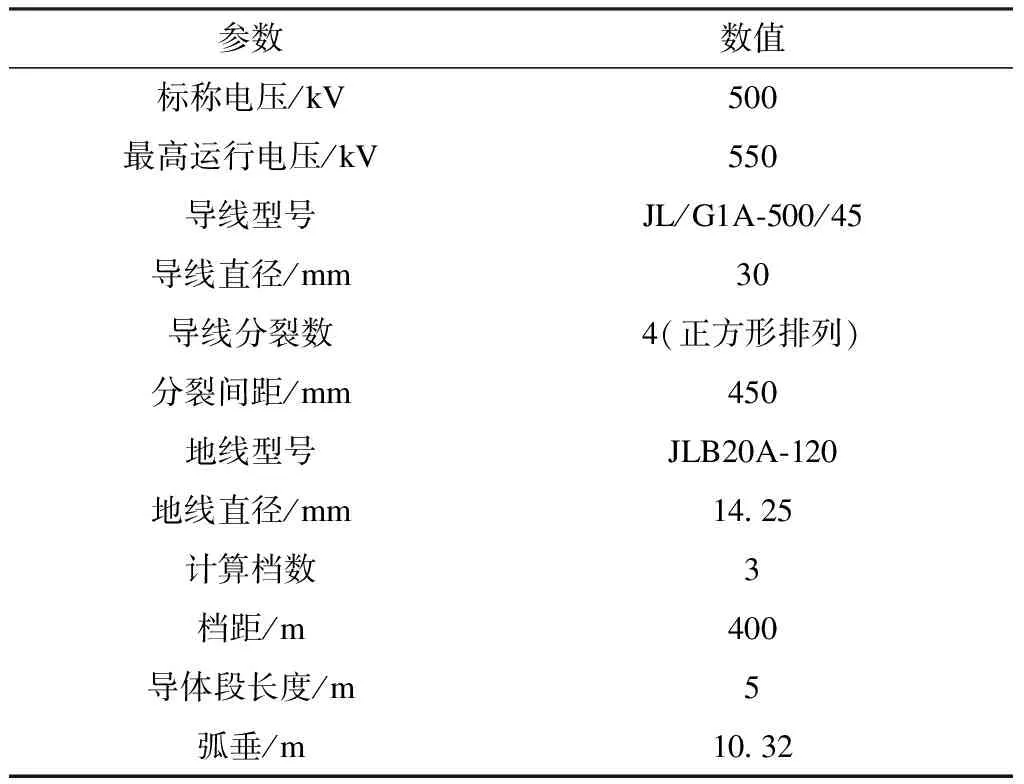
表1 输电线路参数表

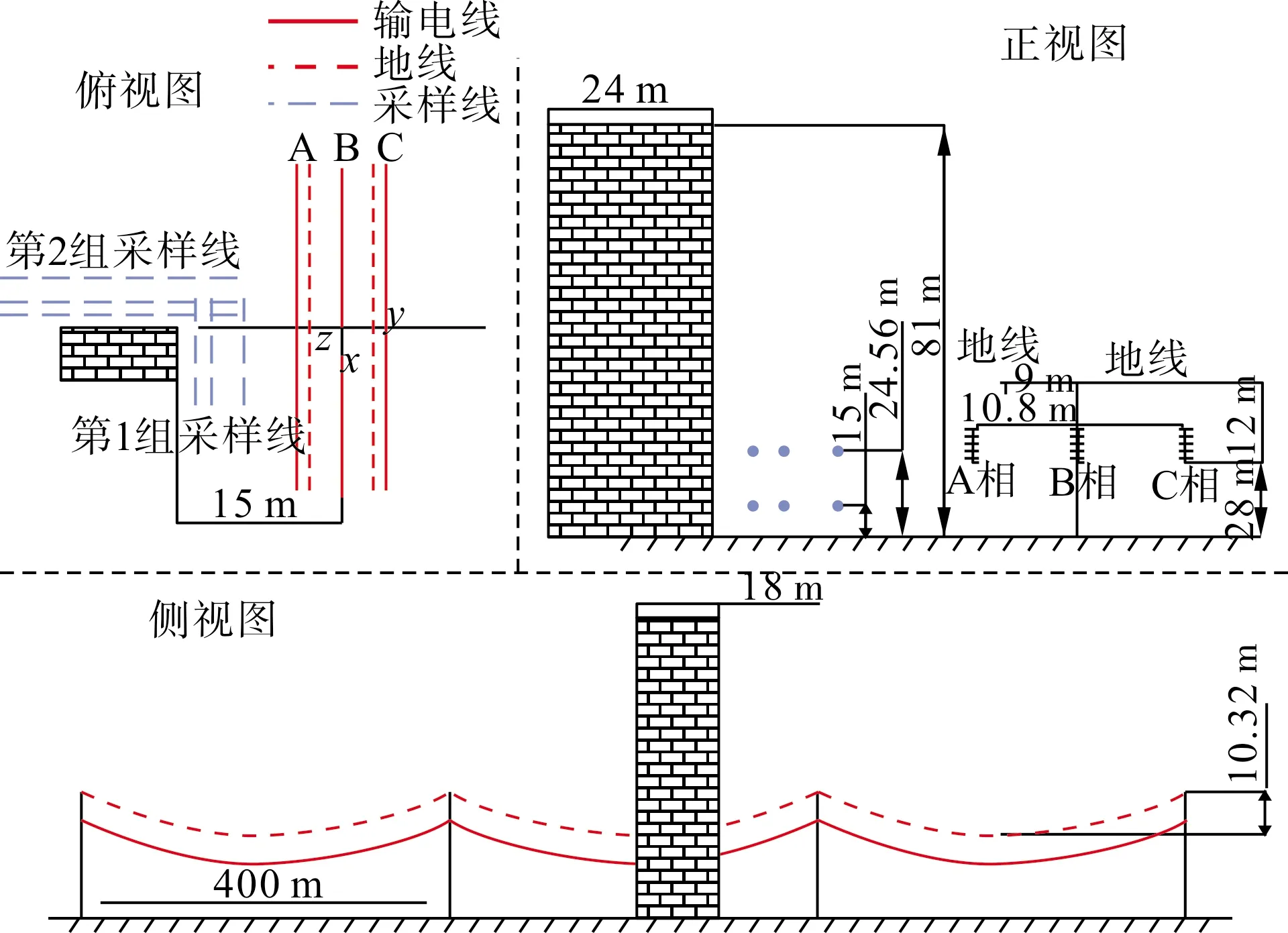
图4 输电线路与建筑物模型三视图

采用模拟电荷法与表面电荷法耦合的数值方法计算3条采样线上存在建筑物时的电场，并将其与不考虑建筑物影响时的电场强度进行对比。第1条采样线上的计算结果如图5所示。根据计算结果可知，存在高层建筑物时，建筑物对临近线路一侧的电场强度有屏蔽作用。

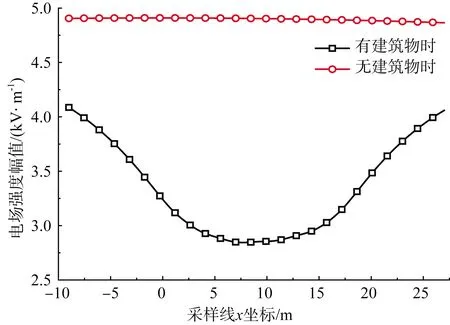
图5 距离建筑物2 m且高1.5 m的采样线上电场强度幅值

为了研究建筑物附近与线路处于近似高度的电场畸变规律，选取的采样线平行于输电线路且位于临近线路一侧的地面上方高度为24.56 m的平面上。此高度为考虑弧垂时输电线路的平均高。设定采样线距离建筑物的距离分别为2 m、4 m和8 m。采用模拟电荷法与表面电荷法耦合的数值方法计算3条采样线上存在建筑物时的电场，并将其与不考虑建筑物影响时的电场强度进行对比。3条采样线的对比结果如图6—8所示。在临近线路的水平面上，建筑物的存在使得原有电场畸变增强。在距离建筑物 2 m、4 m和8 m的采样线上的最大电场强度畸变率(有建筑物和没有建筑物情况下采样线上电场强度最大值的比)分别为48.14%、30.52%和9.46%。

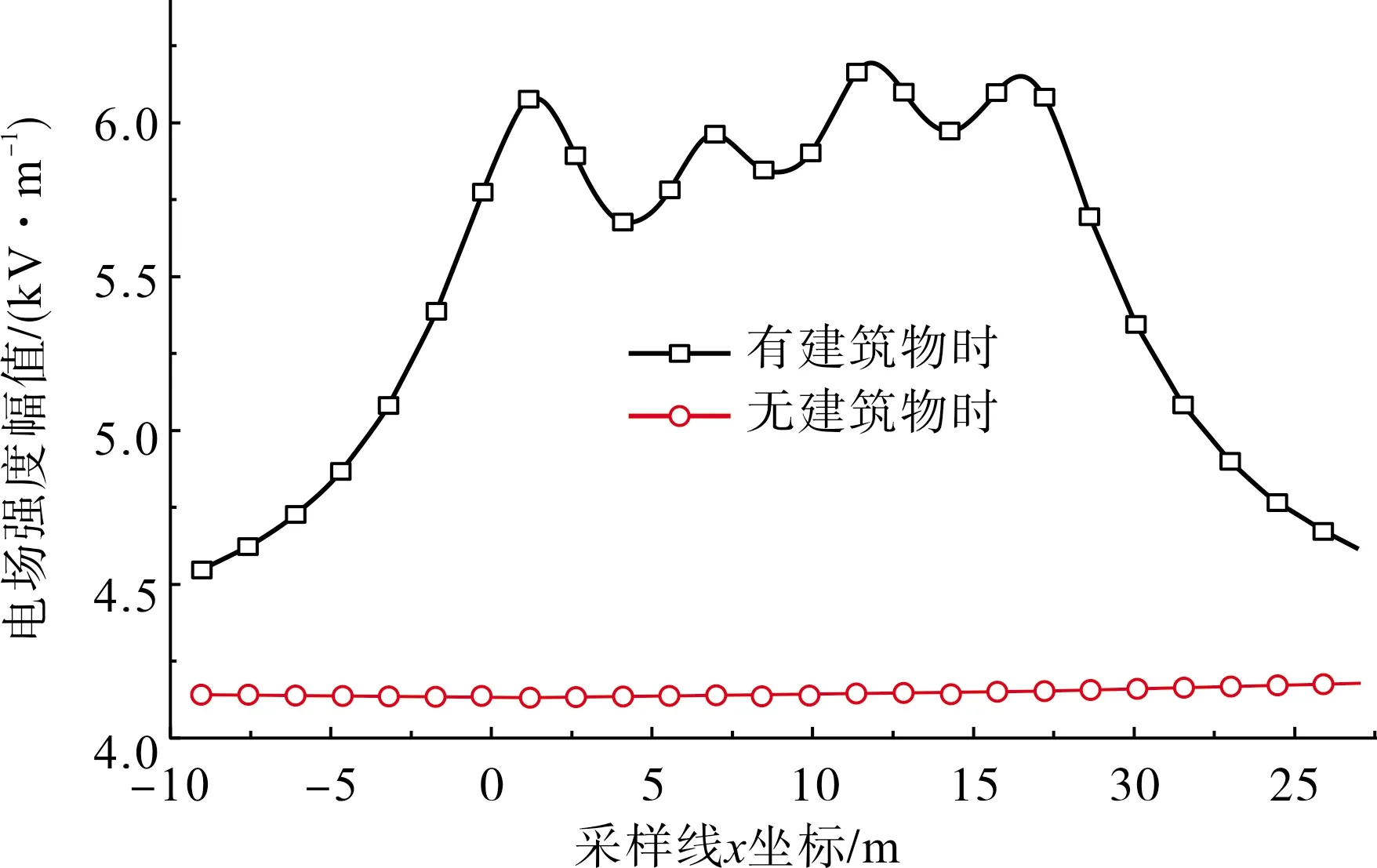
图6 距建筑物2 m且高24.56 m的采样线上电场强度幅值

图7 距建筑物4 m且高24.56 m的采样线上电场强度幅值

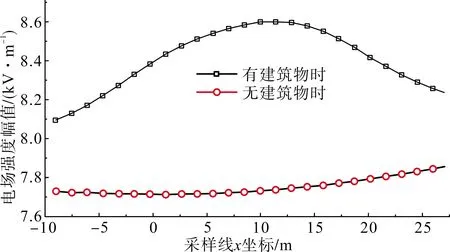
图8 距建筑物8 m且高24.56 m的采样线上电场强度幅值

3 结论

本文构建了基于模拟电荷法和表面电荷法并考虑建筑物影响的交流高压输电线路工频电场数值计算模型。

考虑建筑物的影响时，建筑物对于地面附近的电场强度有屏蔽作用，且越靠近建筑物的区域屏蔽作用越明显；建筑物的存在使得输电线路架设高度附近的电场强度畸变增强，且越靠近建筑物畸变率越大。当多栋建筑物邻近输电线路时，由于相邻建筑物的屏蔽作用，近地处的电场强度会得到进一步的减弱，因此，在实际小区整体存在多个高层建筑的电磁环境评估中，应根据具体计算场景分别予以分析。

现有高压输电线路的电磁环境评价模型是不考虑房屋等大型接地体影响的。本文的数值计算结果表明，房屋的存在使得电场强度变化更为复杂。随着我国城市化进程的不断推进，高层建筑邻近高压交流输电线路的情况已经比较普遍，建议电网公司和环保部门对此开展进一步的研究。